信息诱导对降级路网运行效率的影响*

段倩倩 况爱武,2

(1.长沙理工大学交通运输工程学院 长沙 410004； 2.道路灾变防治及交通安全教育部工程研究中心 长沙 410004)

近年来，随着城市小汽车保有量持续增长，交通拥堵问题日趋严重[1]。国内外研究人员就交通拥堵问题提出了多样化的缓解措施，其中拥挤道路使用先进的出行者信息系统(ATIS)被公认为是缓解拥堵的有效措施。ATIS通过向出行者发布实时交通信息来影响其出行方式或出行路径决策。目前国内外学者在该领域展开了较为深入的研究，Yang等[2]认为配备了ATIS的出行者，可以以确定性用户均衡的方法选择自己的出行路径，相反则只能以随机用户均衡的方法来选择出行路径，况爱武等[3]认为出行者在购买ATIS接收装置时更为关心的是系统所发布的信息的质量；国外的研究同样表明信息环境下的网络性能只能在一定范围内随着ATIS市场渗透率的增加而增加[4]。现有研究大多是对ATIS的市场渗透率及信息质量对路网性能的影响进行研究，而系统信息诱导对降级路网运行效率研究的较少。基于此，本文以降级路网为研究对象，以系统阻抗的倒数为运行效率度量指标，通过构建信息诱导下的路网混合均衡模型来考察在各种不同的需求水平与路网降级程度条件下，信息的质量及其市场渗透率水平对路网运行效率的影响，以期为制订信息发布策略提供更好的决策参考。

1 考虑信息诱导的降级路网混合均衡建模

假定路网的降级由路段容量的随机变化驱动，当路段容量衰减时，路径的行程时间都是随机的，假定有无ATIS接收装置的两类用户均以路径行程时间的均值最小作为路径选择准则。用G=(N,A)表示一个交通网络。其中：N为节点集；A为路段集。Ca为路段a(a∈A)的容量，在本文中假定Ca为随机变量，为使问题简单化，对该问题描述如下；假定路段容量服从均匀分布，将Cad作为均匀分布的上界，即路段的设计容量，Cad的θa倍作为均匀分布的下界(0 ≤θa≤1)，即路段的最小容量，系数θa取值的大小反映了在交通系统条件恶化的情况下路段容量的利用率，θa=1则表示路网不降级，简称为路段容量利用系数。通常情况下采用美国联邦公路局来计算路段行驶时间，即把BPR(bureau of public roads)函数作为阻抗函数，则路段a的行驶时间为

∀a∈A

(1)

由于Ca是随机变量，所以Ta也是随机变量，假定路段容量的随机变化与其流量相互独立。则由均匀分布的特性可以把Ta的均值记为(仅考虑β≠ 1的一般情况)

∀a∈A

(2)

进一步假设路网中各个路段的行程时间是相互独立的，因此该路径的总行程时间可记为组成该路径的各个路段的行程时间均值的和，即

(3)

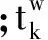
在路网降级的情况下，对于出行者而言无论是否安装ATIS，由于出行者的感知误差，均不能十分准确地掌握路网的实际运行情况，为解决这个问题，引入2个变量，分别为OD对w之间路径k上有无、装置出行者的所感知的行程时间均值，用公式表示如下。

∀w∈W，k∈Rw

(4)

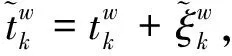
(5)

假定在先进的出行者信息系统环境中，无论出行者是否具有ATIS装置，都随机选择出行的路径，并以感知行程时间均值最小为出行者选择路径的准则，假定两类出行者的感知误差均服从均值为0的独立同耿贝尔分布的随机变量，则根据随机效用和效用化的最大理论，可以知道两类用户都将基于logit概率模型来选择出行的路径，其路径流的分布满足下列公式。

(6)

(7)

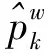
用ηw表示OD对w之间ATIS装置的市场渗透率，定义为有装置需求占总需求qw的比例。那么，对给定的总需求qw和ATIS市场渗透率ηw，在信息系统环境中，因两类用户在同一路网中相互作用而形成的混合随机用户均衡状态等价于寻找一个路径流向量f*∈Ψ，使得如下变分不等式(variational inequality，VI)成立[5]。

(8)

式中：标*的变量为变分不等式模型的解；Ψ为路网中路径流量的可行性解得空间。各个变量满足如下的条件约束。

∀w∈W

(9)

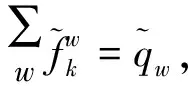
(10)

(11)

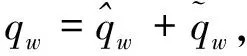
(12)

(13)

2 降级路网混合均衡模型求解算法

相继平均方法(MSA)是求解网络均衡流模型的常用算法，该方法适用性强，但收敛速度较慢。2007年，Liu等[6]对传统的MSA算法进行了改进，Meng等[7]、刘剑锋等[8]均证明了连续权重平均法(MSWA)算法在处理SUE模型时较MSA算法具有更好的收敛性。因此本文为加快算法的运行效率采用了连续权重平均法(MSWA)，利用这种方法来求解VI模型(8)的算法步骤如下。

3 算例分析

算例网络如图1所示，由2个OD对q13，q24，6个节点和7条路段组成，图中线上数字为路段编号。假定网络中各路段的容量服从均匀分布，各路段的特性参数，包括路段自由流时间、设计容量和容量利用率的取值见表1[9]。BPR函数的参数取α=0.15，β=4，迭代精度为ε=10-6。OD需求分别为q13=2 500 pcu/h，q24=2 000 pcu/h。

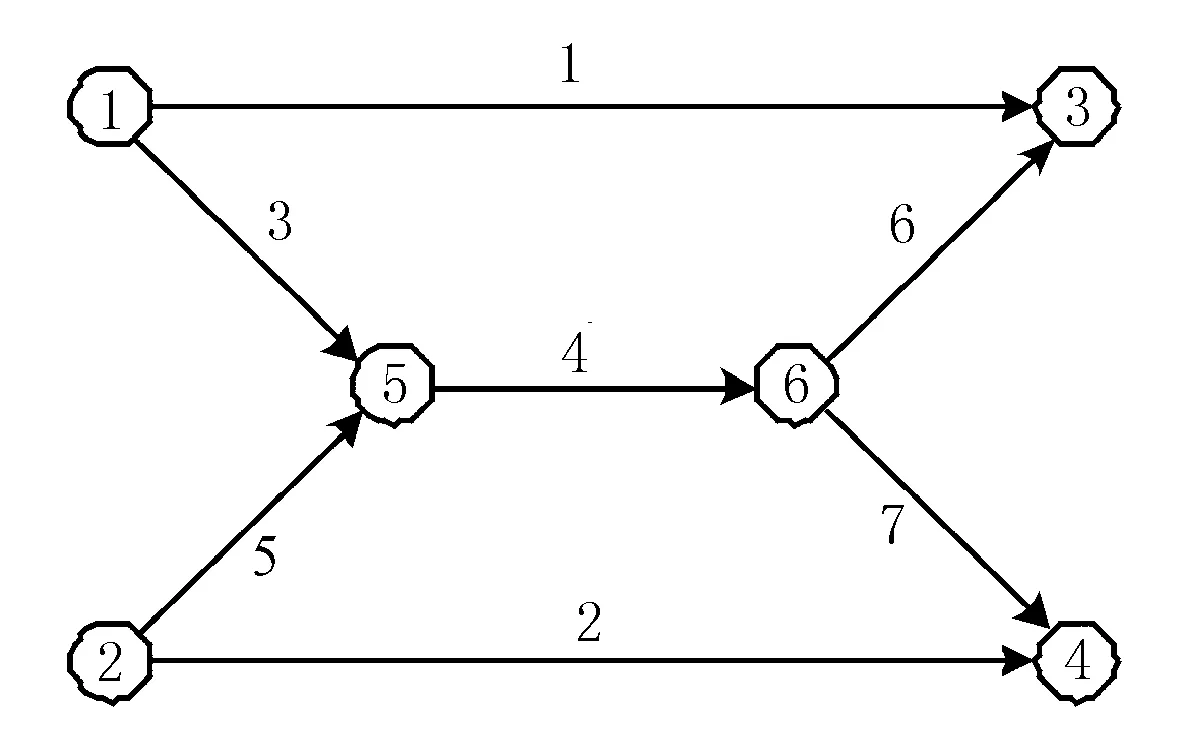
图1 算例网络示意图

路段编号连接节点自由流时间/h设计通行能力/(pcu·h-1)1(1，3)0．820002(2，4)0．920003(1，5)0．220004(5，6)0．625005(2，5)0．320006(6，3)0．325007(6，4)0．42500

本文将阻抗的倒数记为运行效率度量指标，阻抗的单位记为min，运用第3节的求解算法，针对测试路网分析信息系统的市场渗透率、信息质量、路网降级程度以及需求水平对路网效率的影响。

1) 市场渗透率和信息质量(量纲为一的量)对路网总阻抗及运行效率的影响。图2给出了在各种不同的市场渗透率水平下(η=0.2，0.5，0.7，0.9)，路网总阻抗随信息质量的变化规律。

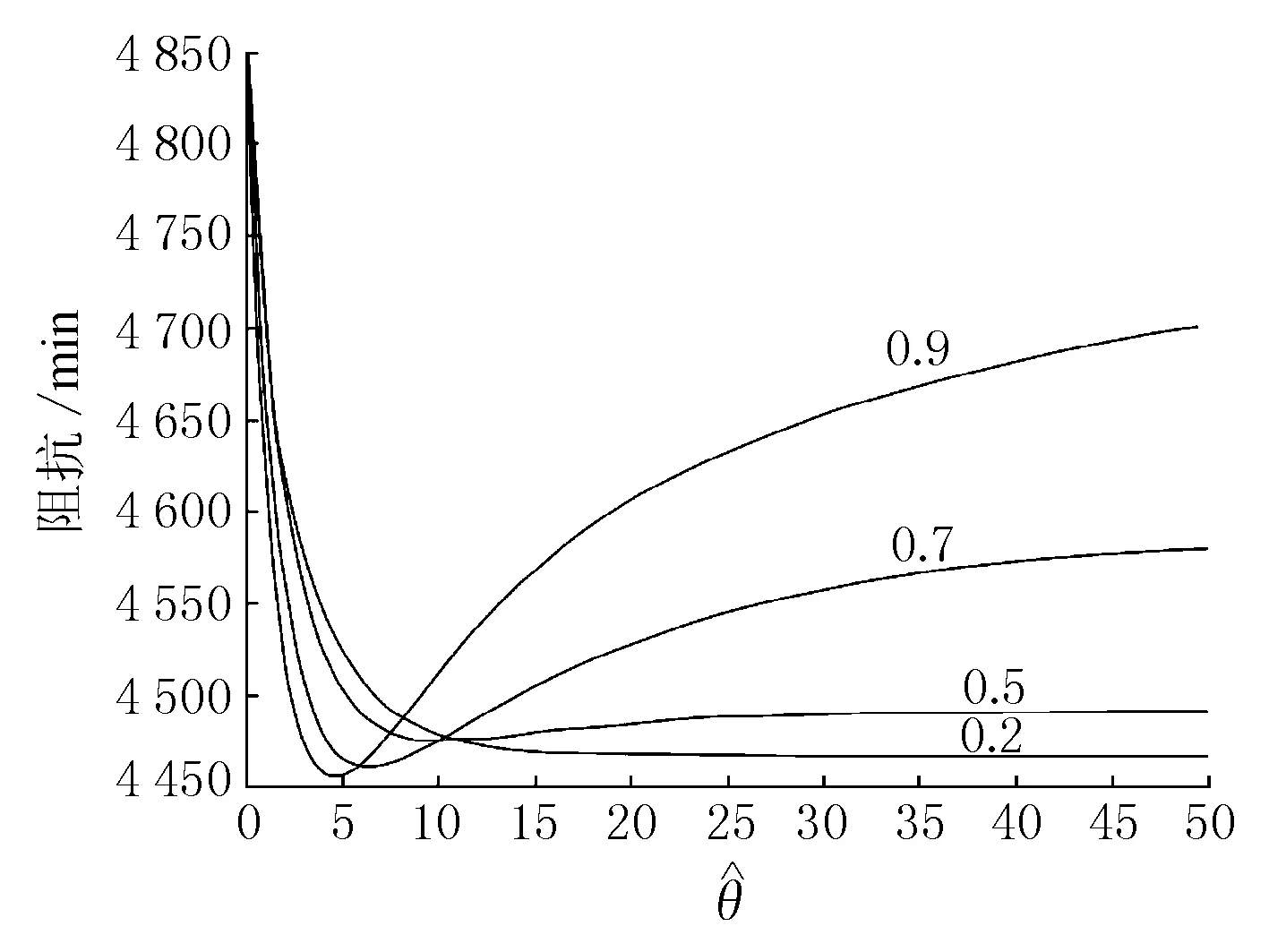
图2 信息质量对路网阻抗的影响

由图2可见，在某一给定的市场渗透率水平下，随着信息质量的增加，测试网络的总阻抗呈现先降后升的趋势。可以发现，在某种最优的信息质量条件下，系统的总阻抗达到最小，然后对信息质量的进一步更新不但不能改善整个网络的运行效率，反而会导致网络总阻抗的增加。一般地，最优的信息质量水平与信息系统市场渗透率的大小相关。

2) 路网降级程度对运行效率的影响。考察路网降级程度对运行效率的影响，分路段容量利用系数θa=0.9，θa=0.8，θa=0.6及θa=0.4共4种情况进行讨论。表2给出了路网在不同降级程度下其阻抗随市场渗透率的变化幅度。

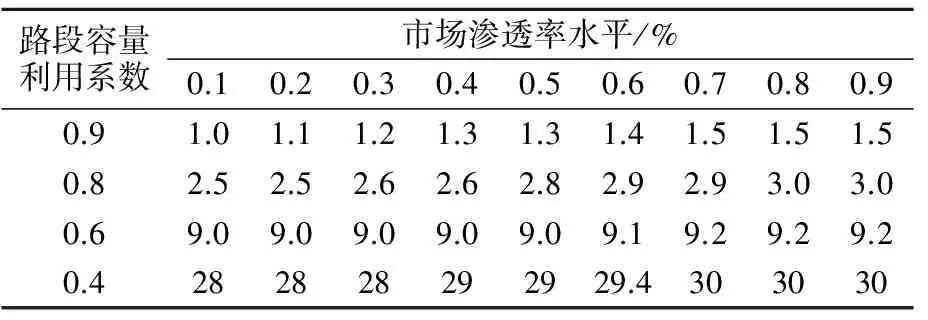
表2 不同降级程度下的路网运行效率变化情况

由表2可见，随着路段容量利用系数θa的减小，路网降级程度加剧，各种不同市场渗透率水平下的系统总阻抗增加，网络运行效率降低，但在同一路网降级条件下，市场渗透率水平对系统阻抗的影响不明显。

3) 交通需求水平和信息质量对路网运行效率的影响。进一步考察需求水平对路网运行效率的影响，设高、中、低3种需求水平的需求量分别为(2 700，2 200)、(2 500，2 000)和(2 200，1 800)。不同需求水平下系统总阻抗的变化见表3。

表3 不同需求水平下的路网运行效率变化情况

由表3可见，由于需求水平不同，路网的运行效率和阻抗也不同。在其他条件相同的情况下，需求小时路网运行效率高，反之在需求大时系统的总阻抗大。随着路网降级程度的加剧，路网运行效率越来越低。

4 结论

1) 无论路网是否降级，合理的ATIS市场渗透率以及适度的信息质量水平能够使得路网获得最佳的运行效率。

2) 路网降级会对其运行效率产生影响，但路网运行效率的下降既与路网降级程度有关，又与OD对间的交通需求水平相关。

3) 在信息系统的渗透率较小时，未配备装置的出行者对路网的熟悉程度是影响运行的主要因素，当信息系统的渗透率较大时，信息质量对路网运行效率有显著影响。无论路网降级程度如何，信息质量水平都应控制在一个合理的范围内才能使得路网运行效率较高。

[1] 黄中祥，况爱武，范文婷，等.出行信息对道路网络出行时间可靠性的影响[J].交通运输系统工程与信息，2012(12).93-99.

[2] 况爱武，黄中祥，张生.ATIS影响下基于广义出行负效用的随机分配[J].系统工程，2010(10)：108-113.

[3] 况爱武，王正武.ATIS影响下的混合用户均衡交通分配模型研究[J].重庆交通学院学报，2006(6):108-114.

[4] EMMERINK R H.M，AXHAUSEN K W,NIJKAMP P，et al. Effects of information in road transport networks with recurrent congestion[J]. Transportation Research,Part A.1995(22):21-53.

[5] 况爱武，唐志强，黄中祥.不确定供给对诱导系统均衡市场渗透率的影响[J].北京：北京工业大学学报，2014(6)：179-184.

[6] LIU H, HE X Z, HE B S. Method of successive weighted averages (MSWA)and self-regulated averaging schemes for solving stochastic user equilibrium problem [J].Networks and Spatial Economics,2009(4):505-524.

[7] 刘剑锋.基于换乘的城市轨道交通网络流量分配建模及其实证研究[D].北京，北京交通大学，2012.

[8] MENG M,SHAO C F,ZHENG C X, et al. Stochastic user equilibrium with combined mode in a degradable multi-modal transportation network[J]. Journal of Computers,2012(12):3005-3012.

[9] 况爱武.基于可靠性的城市交通网络分析[D].长沙：长沙理工大学，2012.