隧道衬砌结构在水压力作用下受力计算分析

2018-04-23刘善琪申志军李小青

交通科技 2018年2期

黄丹刘善琪申志军李小青

(1.华中科技大学土木工程与力学学院武汉 430074; 2.湖北联合交通投资开发有限公司武汉 430000; 3.蒙西华中铁路股份有限公司北京 100073)

对于岩溶隧道衬砌结构来说，水压力是作用于其上的主要荷载[1]，如何在不影响生态环境的条件下，安全、可靠地进行隧道设计、施工和运营[2]，一个关键的问题即如何确定衬砌上水压力的大小。以往研究地下水问题多针对具体工程，研究地下水在工程结构中的流量、结构的防排水和对地下水的处理等方面[3-4]，而对结构承担水压力的问题研究不多[5]。由于隧道衬砌结构是在地层中修建的，其工程特性、设计原则及方法与地面结构不同，隧道结构变形受周围岩土体本身的约束，衬砌结构与围岩之间相互作用，衬砌结构变位由主动荷载和围岩弹性抗力共同作用产生，而弹性抗力的大小和范围取决于结构变位，所以隧道衬砌结构的受力计算分析非常复杂，考虑因素较多，常规计算方法很难得到结果。目前有限元数值解析法广泛运用于隧道结构计算中，ANSYS软件是世界上最为通用的有限元软件，其强大的处理功能可以方便地实现隧道衬砌结构的受力计算[6]。

本文采用基于ANSYS的隧道衬砌结构分析方法，对隧道支护结构体系按照荷载-结构模型进行验算，然后再借助ANSYS有限元软件进行隧道结构在水压力作用下的受力分析。

1 数值模拟模型建立

基于ANSYS的隧道结构受力特征有限元分析步骤为：建立有限元模型；按照标准断面建立衬砌结构几何模型，并采用梁单元模拟；施加围岩压力和衬砌重力，围岩和二次衬砌之间的相互作用通过在单元的节点上施加径向弹簧进行模拟，设定边墙底端位移边界条件[7]。

求解有限元模型，先进行初步求解，通过后处理程序查看衬砌结构弹簧受力状况。根据结构荷载法假定地层弹簧不能承受拉力，故应在模型中删除受拉弹簧，然后重新进行分析计算，并查看和删除受拉弹簧。重复以上求解步骤，直到去除所有受拉弹簧，则剩余的受压弹簧所在的范围即为弹性抗力的范围。最后，进行正式求解，所得的弯矩、轴力、剪力值用于结构安全分析。

某隧道衬砌结构设计见图1，采用荷载-结构计算方法建模，模型如图2所示，二次衬砌采用弹性平面梁单元模拟，围岩弹性抗力采用弹性链杆模拟。

图1 隧道衬砌结构设计图(单位：cm)

图2 衬砌结构受力ANSYS计算模型

1.1 围岩压力

隧道开挖及现场围岩压力量测的实践表明，围岩压力值受到众多因素影响，但主要取决于岩体的构造和结构面组合等地质因素。压力分布通

常很不均匀，且岩质多裂隙岩体比土质岩体中的压力分布更不均匀。基于这些情况，结合我国400余座铁路隧道施工塌方资料进行的统计分析，TB 10003-2016 《铁路隧道设计规范》[8]提出可用式(1)确定作用在结构上的垂直均布荷载。

Q=0.45×2S-1·γ·ω

(1)

式中：Q为垂直均布围岩压力，kPa；S为围岩级别；γ为围岩的天然重度，kN/m3；ω为宽度影响系数，ω=1+i(B-5)。其中：B为隧道开挖宽度，m；i为B每增加1 m时围岩压力增减率，当B<5 m时，取i=0.2，当B>5 m时，取i=0.1。

围岩水平均布侧向压力e与垂直均布压力Q之间的关系如表1所示。

表1 围岩水平均布压力

1.2 衬砌结构自重

隧道衬砌结构自重荷载可根据衬砌结构的厚度、计算宽度及结构材料重度等参数，按照式(2)计算。

Q2=HBγ

(2)

式中：Q2为自重荷载，kN/m；H为构件计算截面的设计厚度，m；B为构件计算截面的设计宽度，m；γ为结构材料重度的标准值，kN/m3。

1.3 衬砌水压力

对所采用的实际荷载模型进行数值模拟，考虑围岩应力全部作用在二次衬砌结构上，且作用在衬砌结构上的水压力采用长期监测数据中峰值取0.2 MPa，也全部作用在二次衬砌上。

1.4 被动荷载

即围岩的弹性抗力。所谓弹性抗力就是指由于支护结构发生向围岩方向的变形而引起的围岩对支护结构的约束反力。目前多用温克勒假定为基础的局部变形理论计算。该理论认为围岩弹性抗力与围岩在该点的变形成正比，用公式表达为

σi=Kδi

(3)

式中：δi为支护结构表面某点i的位移，m；σi为在该店处围岩和结构相互作用的反力，MPa；K为围岩的弹性抗力系数，MPa/m。

对于列车荷载、地震力荷载等其他荷载，一般情况可以忽略不计算。

根据隧道衬砌水压力长期监测数据，取衬砌水压力峰值为计算水压荷载，土压荷载考虑自重应力场及构造应力场作用，按水土合算考虑，荷载的计算结果见表2。

1.5 模拟计算参数的选取

考虑到注浆加固改良地层的作用，围岩参数按V级围岩选取，材料物理学参数见表3。

表3 材料物理力学参数表

2 计算结果分析

通过数值计算得到衬砌受力大小，绘制受力图。衬砌结构变形图见图3。长期水压0.2 MPa

下隧道衬砌结构弯矩图见图4、结构轴力图见图5、结构剪力图见图6。弯矩单位为N·m，轴力单位为N。

图3 衬砌结构变形图

图4 长期水压0.2 MPa下衬砌结构弯矩图

图6 长期水压0.2 MPa下衬砌结构剪力图

由结构变形图、弯矩图、轴力图和剪力图可得如下结果。

1) 结构最大变形量为0.002 4 m，说明在0.2 MPa的峰值水压力作用下，隧道结构几乎不产生形变，结构稳定。

2) 结构仰拱和边墙脚处为弯矩最大点，仰拱位置弯矩值为344.87 kN·m，梁单元上侧受拉；边墙角位置弯矩为372.46 kN·m，梁单元下侧受拉。

3) 仰拱处出现轴力最大值1 150.1 kN，为危险截面位置。左、右边墙脚处的剪力最大，同样为不利截面位置，所以通过数值模拟结果可以选择仰拱、边墙角处这两处危险截面进行结构安全度分析。根据围岩压力实测数据分析结果，确定了拱脚位置也需进行结构安全性验证与预测，因此还选择了拱脚测点进行安全度计算分析。

3 衬砌结构受力及安全度分析

3.1 衬砌结构安全性分析方法

衬砌结构安全度分析，计算各断面最不利位置的偏心距、安全系数；按TB 10003-2016 《铁路隧道设计规范》破损阶段法验算衬砌截面强度。

K=N极限/N

(4)

式中：K极限为截面的极限承载力或轴力，kN；N为截面的实际轴力，kN；K为强度安全系数。

对于截面极限承载力N极限的计算，依轴向力偏心距e0=M/N的大小有2种情况。

1) 对混凝土矩形截面构件，当e0≤0.20h时，抗压强度控制承载能力，不必验算抗裂。

N极限=φαRabh

(5)

2) 当e0>0.20h时，系抗拉强度控制承载能力，不必验算抗压。

(6)

式中：Ra为混凝土抗压极限强度，MPa；Rl为混凝土抗拉极限强度，MPa；b为截面宽度，m；h为截面厚度，m；α为轴力偏心影响系数，可由e0/h值查得。按规范当α>1时取α=1，当α≤1时，α=1+0.648(e0/h)-12.569(e0/h)2+15.444(e0/h)3；φ为构件纵向弯曲系数，对于隧道衬砌可取φ=1。

3.2 衬砌结构内力及安全系数计算结果

将选择的仰拱中部、边墙角和拱脚这3个安全度计算点，按照安全度准则进行衬砌结构安全分析，分析结果见表4所示。

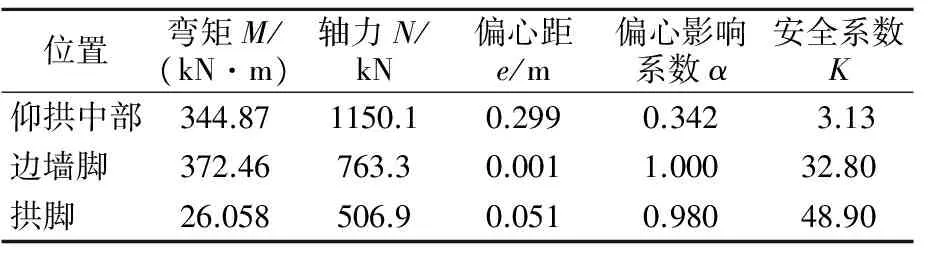
表4 水压0.2 MPa作用下衬砌结构关键点应力及安全系数

由表4可见，仰拱位置计算得到的安全系数为3.13，基本满足规范中要求的最低安全系数2，满足强度要求；衬砌边墙整体结构呈现受拉控制，经过计算得出边墙脚处的安全系数为32.8，远高于规范中要求的结构安全系数；拱脚位置计算得到的安全系数为48.9，高于规范要求的结构安全系数。计算结果表明，隧道衬砌结构在长期峰值水压力作用下，安全度满足规范要求，结构安全稳定。

4 衬砌结构内力现场监测结果

4.1 二次衬砌内力变化特征分析

经过长期的现场监测，得到二次衬砌在长期水压及围岩压力作用下内力时态曲线，如图7所示。

图7 二次衬砌应力运营期时态曲线

根据断面各测点处的二衬内力平均值绘制二次衬砌内力分布图，如图8～10所示。其中应力值“+”值表示受拉，“-”值表示受压。

由以上二衬内力时态曲线及衬砌结构内外侧内力分布图可以看出。

1) DK365+111断面内，拱顶内侧测点处二衬内力为最大拉应力，均值为71.46 MPa；从图7a)二衬内力时态曲线变化规律看出，其大小总在 40～100 MPa范围内变化，并呈现逐渐减少趋势。仰拱内侧测点处衬砌内力为最大压应力为30.22 MPa，变化曲线平稳，变化幅度不大。边墙、拱脚、拱腰内外侧的二衬内力均在10～40 MPa范围内变化，均为拉应力，变化幅度较小。

图8 断面DK365+111二衬钢筋应力分布图(单位：MPa)

图9 断面DK365+315二衬钢筋应力分布图(单位：MPa)

图10 断面DK365+331二衬钢筋应力分布图(单位：MPa)

2) DK365+315断面内，右拱腰内侧测点处的二衬内力最大，均值为-227.2 MPa，为压应力；从图7b)二衬内力时态曲线变化规律看出内力值随时间变化范围较小，变化幅度也不大。在仰拱内侧和拱顶内侧位置测到最大拉应力，在63.3 MPa左右，时态曲线显示其变化趋势稳定。

3) DK365+331断面内，右拱脚外侧测点处出现最大压应力，均值为76.21 MPa；从图7c)中二衬内力时态曲线变化规律看出，右拱脚测点处应力值随时间变化幅度很小，变化稳定。但由于元件断电，造成后面部分数据缺失。其它测点处衬砌内力变化幅度较小，且变化趋势平稳。

4.2 模拟结果与实测数据对比分析

现场实测数据分析结果表明，隧道各监测断面二次衬砌钢筋内力测量值在运营期基本稳定，各测点数据趋势平稳；二次衬砌钢筋内力最大值约为227.2 MPa，为压应力，发生在DK365+315断面右拱腰测点处；衬砌结构仰拱、拱脚、拱顶位置处出现过较大应力；由于隧道结构采用加强型复合式衬砌，二次衬砌钢筋应力在设计压力值范围以内，隧道结构受力完全正常。

通过对衬砌结构受力进行数值模拟计算，由结果可以看出，隧道衬砌结构在峰值水压力的作用下，其二次衬砌结构满足安全系数要求，边墙和仰拱为受力最不利位置，仰拱位置安全系数较小，但也满足安全系数要求。现有二次衬砌设计已能满足结构强度要求，衬砌结构安全稳定。拱脚位置为实测围岩压力最大点，计算所得结构安全系数较高，满足结构最低安全系数要求。

对比数值模拟结果与实测数据可得，两者分析结果中应力分布规律大致相同，两者均出现了仰拱和边墙两处最不利位置。

数值模拟中安全系数计算结果显示结构处于相对安全状态，实际检测结果也显示，二衬内力峰值也均在设计安全范围之内，结构本身受力较小，表示结构相对安全。具体数值有出入是因为数值计算将模型简化为均匀介质，没有考虑到实际工程中地质条件的非均匀性及注浆效果。