基于偏差耦合的免疫单神经元PID同步控制
2018-04-20张兴鹏
王 萍,张 俊,张兴鹏
(1.安徽三联学院电子电气工程学院,合肥230601; 2.合肥铭远电气科技有限公司,合肥230031)
0 引言
在实际的工业化生产中,多电机同步协调控制问题广泛存在于各个工业自动化生产系统中[1]:如造纸机、同步轧机等,需要多台电动机的转速保持一定比例同步运行;又如数控加工机床、机器人控制等,需要多台电动机的输出转角按某种特定关系运转。在这些控制系统中,由于受到外部负载扰动、电机参数不匹配以及其他不确定因素的影响,导致电机间的同步性能变差,因此,协调好各个电机间的同步运行性能直接关系到系统的稳定性和控制精度。
早期保持多电机同步运行采用非耦合控制策略,主要有并行和主从两种结构[2]。针对非耦合控制中各轴间动态性能不匹配的难点,Koren[3]在1980年提出了只适用于两台电机的交叉耦合控制策略。Shih等[4]在2002年提出相邻交叉耦合控制,即任一台电机只考虑与其相邻的两台电机的运动情况[5],这种控制会导致控制延时,造成同步误差。2003年Perez-Pinal F等[6]提出了偏差耦合控制,这种控制策略将系统中各个电机的速度反馈值集合到一个“速度补偿器”模块进行比较运算,得到各电机间的误差总和信号,补偿电机速度,这种控制方式可适用于多电机系统,具有很好的同步控制性能。
永磁同步电动机(PMSM)是一个高阶、非线性、强耦合的多变量系统,采用矢量控制方法,速度环用传统的增量式PID算法进行控制,难以达到满意的同步控制高精度的要求。为实现PID参数整定不依赖被控对象数学模型,而且PID参数能在线整定,满足实时控制的要求,自适应PID控制成为解决这一难题的有效途径。文献[7]结合滑模变结构和模糊控制方法,设计了模糊滑模PI控制器,对多电机系统进行同步控制,但模糊规则的制定过于依赖操作者的经验,参数整定困难,缺乏自学习性。文献[8]采用神经网络PID控制器实现多电机同步控制,神经网络虽然具有良好的自学习和自适应能力,但计算复杂,时效性较差。本文采用单神经元自适应PID控制器,结合T细胞免疫反馈机理,形成一种免疫单神经元PID(ISNPID)控制器。一方面利用单神经元的自学习、自适应能力,有效克服负载扰动、被控对象参数变化等一些因素的影响,使控制系统具有良好的控制精度、较快的收敛速度以及较强的鲁棒性;另一方面又提高了单神经元的学习速度,缩短了响应时间,改善了控制器性能。通过对4台电机的同步控制性能进行仿真研究,证明了这种算法的有效性。
1 偏差耦合控制结构
如图1和2所示为4台电机偏差耦合控制结构。Kir为速度补偿器增益,作用是补偿各电机间转动惯量的不同,Kir=Jr/Ji,i=1,2,3,4,r=1,2,3,其中i表示电动机序号,Jr表示与电机i相邻的第r个电机的转动惯量。

图1 4电机偏差耦合同步控制结构图
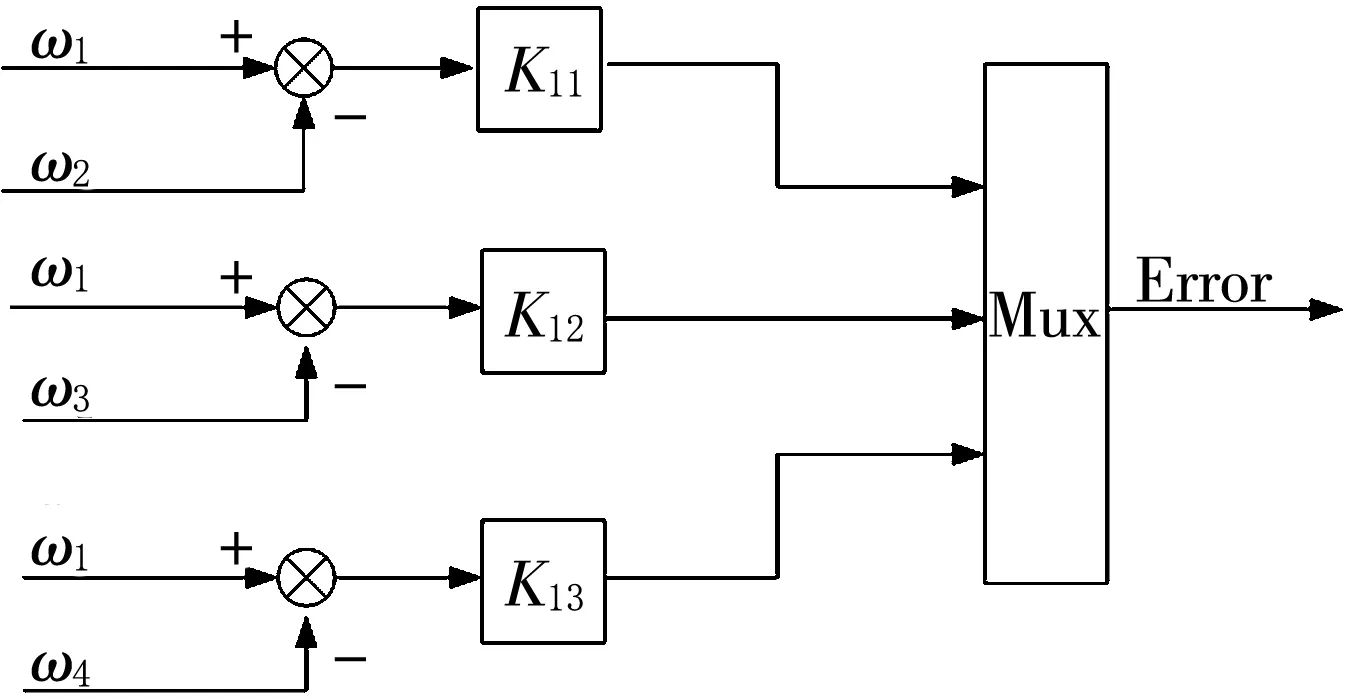
图2 电机1的速度补偿器
2 免疫单神经元PID算法
2.1 单神经元自适应PID控制器
图3中转换器的输入值为设定值yd(k)与输出y(k),转换器的输出为神经元学习所需要的3个状态量x1(k)、x2(k)、x3(k)。在这里性能指标为
(1)
式中K为神经元控制器增益,K>0。
(2)
△u(k)=K{w1(k)e(k)+w2(k)[e(k)-e(k-1)]+w3(k)[e(k)-2e(k-1)+e(k-2)]},
(3)
式中:wi(k)为对应于xi(k)的加权系数;Δu(k)为第k次采样的控制器输出增量。
针对单神经元自适应PID控制算法,许多专家学者进行了多方面的深入研究,进而产生了许多改进的控制算法,其中一种是修改算法中加权系数的学习修正部分,将其中的xi(k)改为e(k)+Δe(k),改进后的有监督的Hebb学习规则算法表达如下:
(4)
(5)
(6)
式中Δe(k)=e(k)-e(k-1)。
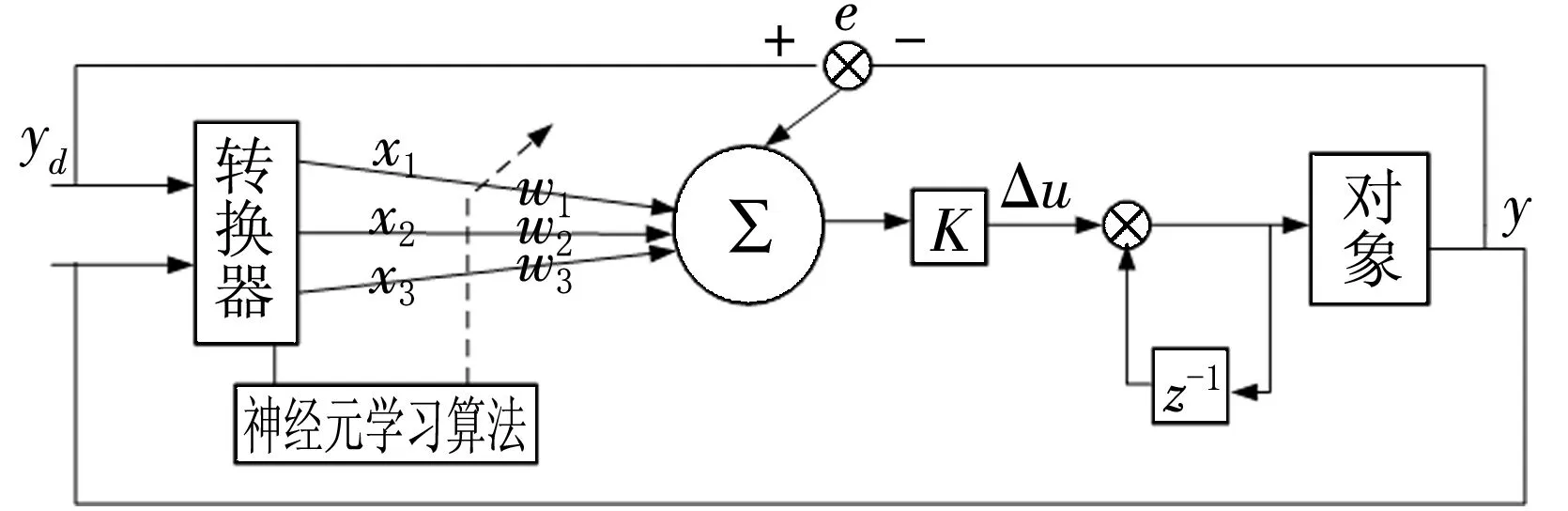
图3 单神经元自适应PID控制器结构
针对单神经元自适应PID控制器中存在的不能实时调整增益、响应速度慢等问题,本文在单神经元PID控制算法中引入T细胞免疫反馈机理,从而形成一种自动调节增益的免疫单神经元PID控制算法[9],以提高单神经元PID控制器的学习及动态响应速度,改善控制器性能。
2.2 神经元增益的免疫自调整
根据体液免疫过程(图4所示)得出适用于控制系统的免疫调节器的基本模型:定义第k代的抗原摩尔浓度为ε(k),由抗原刺激的TH细胞输出为TH(k),TS细胞对B细胞的影响为TS(k)(虽然TS细胞对TH和B细胞都有抑制作用,简单起见,主要考虑TS对B细胞的抑制),则第k代B细胞的摩尔浓度可表示为:

图4 免疫反馈机理示意图
B(k)=TH(k)-TS(k),
(7)
TH(k)=K1ε(k),
(8)
TS(k)=K2{f[ΔB(k)]}ε(k),
(9)
式中:K1为TH细胞促进因子;K2为TS细胞抑制因子;ΔB(k)=B(k)-B(k-1)为B细胞摩尔浓度的变化;f(·)为非线性函数,与B细胞摩尔浓度的变化有关,表示在第k代时,B细胞分泌产生的抗体和抗原互相作用得到的免疫效果。
由式(7)~(9),可得B细胞的摩尔浓度与抗原量浓度的关系式:
B(k)=K1ε(k)-K2{f[ΔB(k)]}ε(k)=K′{1-ηf[ΔB(k)]}ε(k),
(10)
式中:K′=K1;η=K2/K1,表示TS与TH作用的比例系数。
将抗原摩尔浓度ε(k)表示偏差e(k),B细胞的摩尔浓度B(k)表示控制输入u(k),有下列控制规律:
u(k)=K′{1-ηf[Δu(k)]}e(k)。
(11)
从式(11)可知,由免疫反馈机理得到的控制器是一个非线性比例控制器,比例增益为
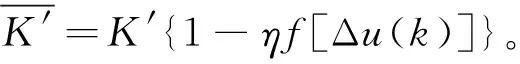
(12)
对于单神经元增益K,应随系统的实时误差进行相应调整,由K值对系统动态调节的影响可知,响应初期偏差值较大时,应增加控制取较大K值,加快响应速度;在接近稳态时,偏差较小,应减小K值,以避免系统出现大的超调和振荡。K值调整的过程相似于免疫反馈机理,因此可在K的自调整中引入免疫调节机理。
根据文献[10]选择免疫调节函数
K=f(e)=km(1-ηexp(-αe2)),
(13)
式中:km为比例系数,控制免疫调节反应速度;η为控制稳定效果;α为影响免疫调节曲线的坡度。
3 PMSM伺服系统矢量控制
采用id=0转子磁场定向的矢量控制PMSM伺服系统如图5所示。主要由以下部分构成:
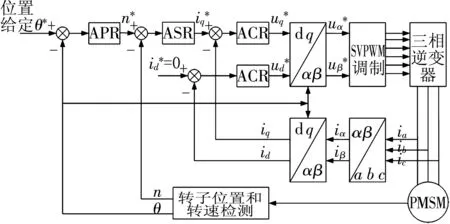
图5 基于id=0的PMSM伺服控制系统结构
1)位置控制器(APR)、速度控制器(ASR)、电流控制器(ACR)。
2)电动机转子位置、转速检测模块。
3)坐标变换模块。
4)SVPWM模块和三相逆变模块。
4 仿真研究
4.1 仿真参数
4台PMSM的参数设置见表1。此外,直流母线电压Udc=400V,逆变器开关频率10 kHz。
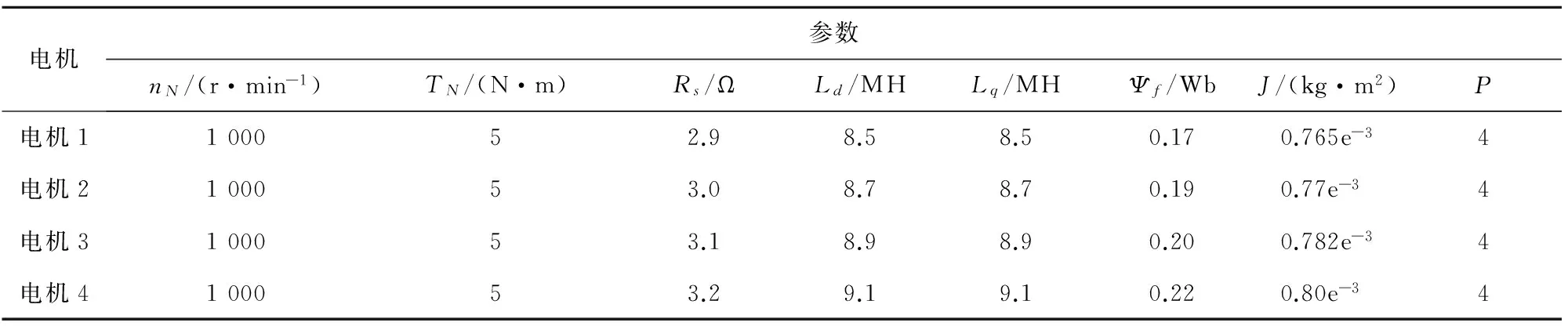
表1 4台电机参数
常规PI控制器速度环的PID控制器参数经过多次调试,选取了总体性能较好的一组,参数为Kp=0.04,Ki=0.7,Kd=0;电流环的两个PID控制器参数相同,Kp=200,Ki=40,Kd=0。ISNPID控制器w1(0)=w2(0)=w3(0)=0.1,ηP=0.9,ηI=0.2,ηD=0,比例因子km=0.1,函数坡度α=0.1×10-4,控制稳定度η=0.1。
4.2 仿真条件
整个系统4台电机的给定参考转速为nN=1 000 r/min,仿真时间为1 s。启动时4台电机加上相同的负载TN=5 N·m,在t=0.08 s时,将电机1和3的负载转矩由5 N·m分别突变为7 N·m和9 N·m,其余两台电机保持不变。
4.3 实验结果
4电机速度环控制改为ISNPID控制,并与常规PID控制进行对比,仿真得到4电机跟踪误差曲线如图6~7所示,同步误差曲线如图8~9所示。各电机之间的跟踪误差和同步误差对比图,如图10(a)~(d)和图11(a)~(f)所示,图中实线表示采用ISNPID控制器,虚线则为常规PID控制器。
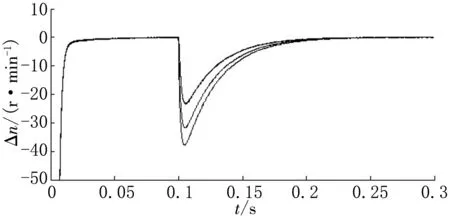
图6 PID四电机跟踪误差
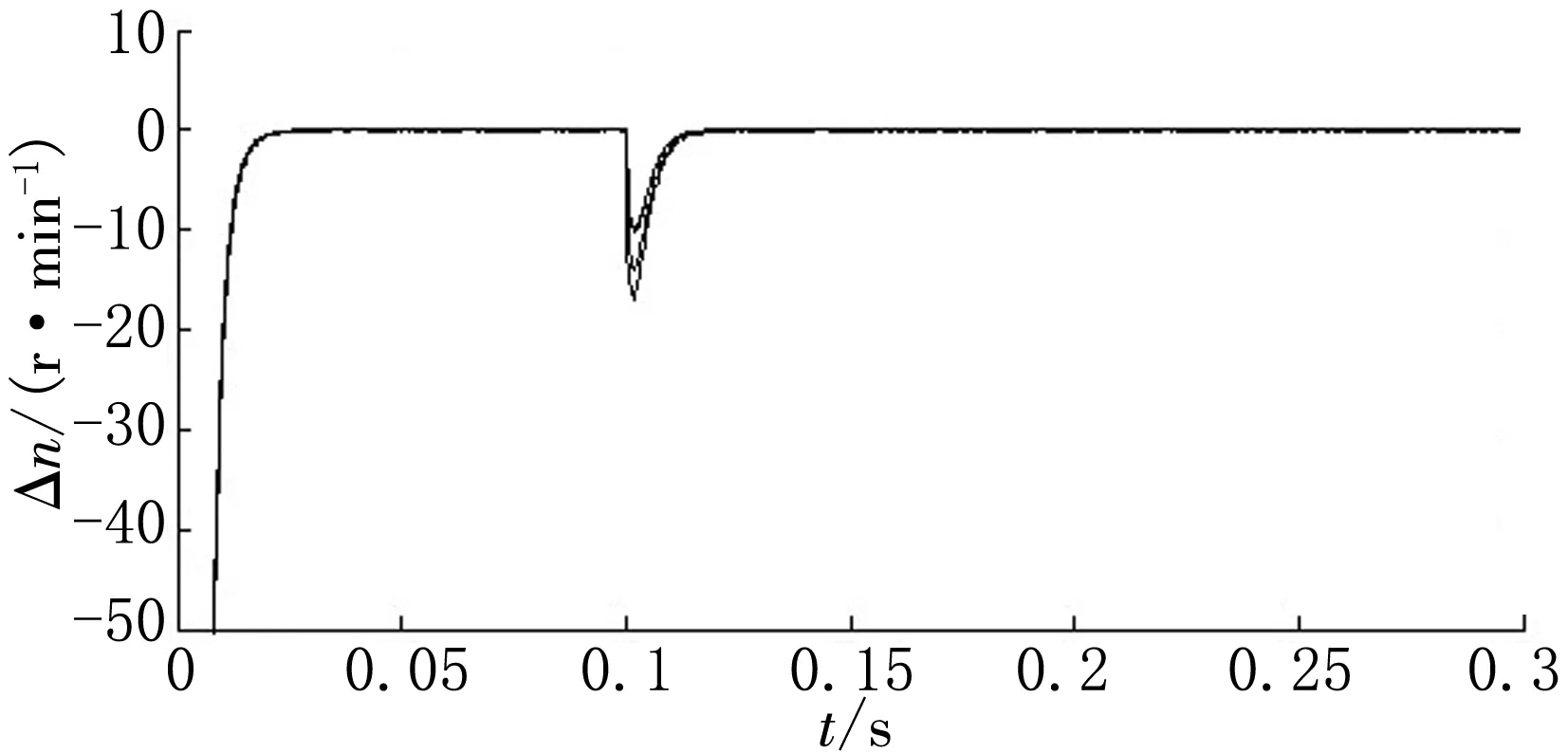
图7 ISNPID四电机跟踪误差

图8 PID四电机同步误差

(a)电机1跟踪误差
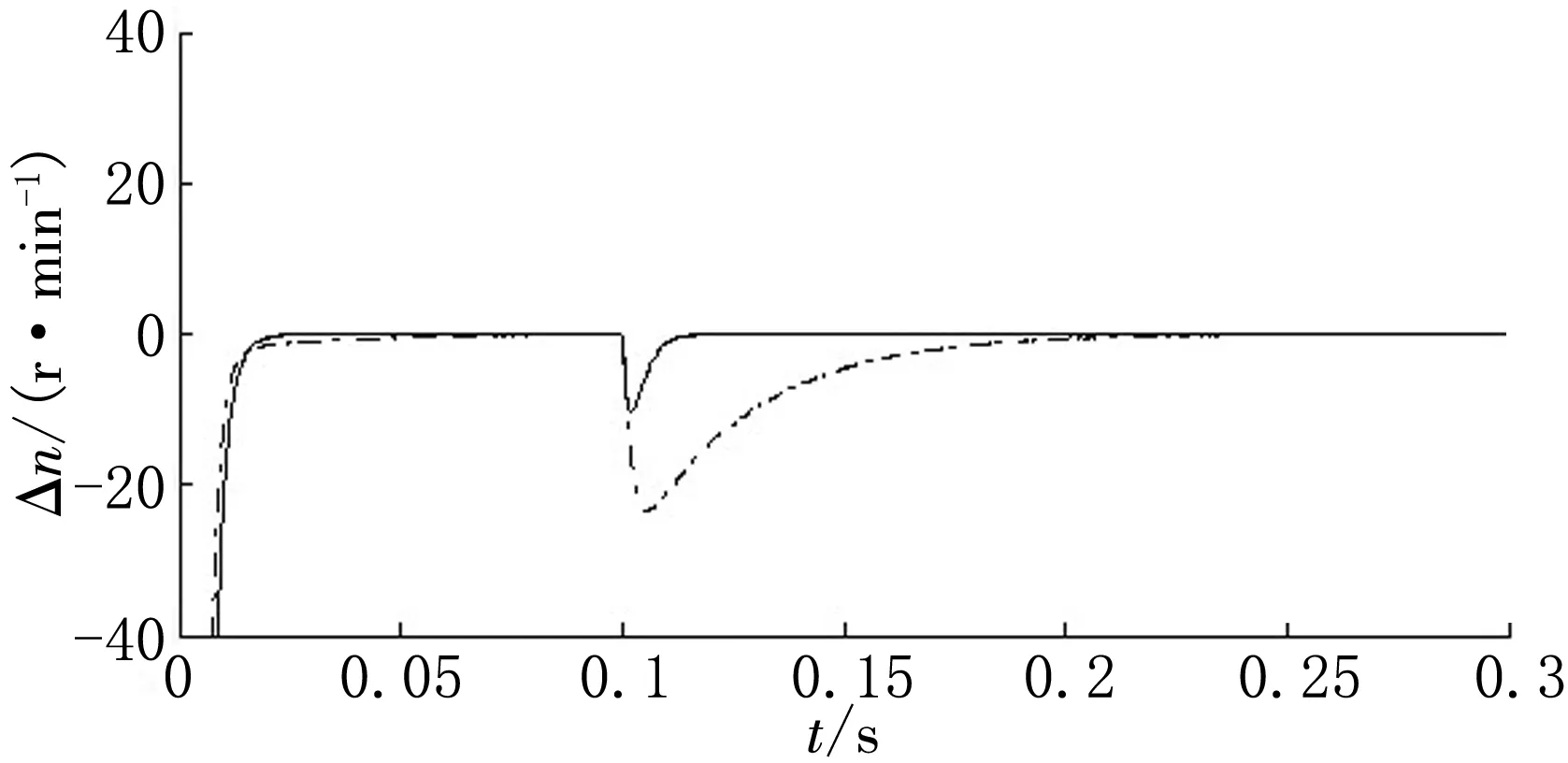
(b)电机2跟踪误差

(d)电机4跟踪误差图10 四电机跟踪误差曲线
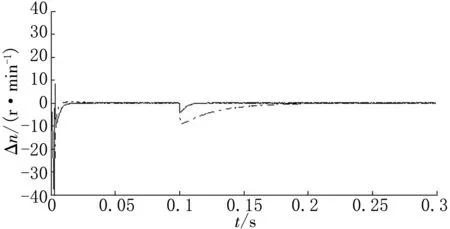
(a)电机1、2同步误差
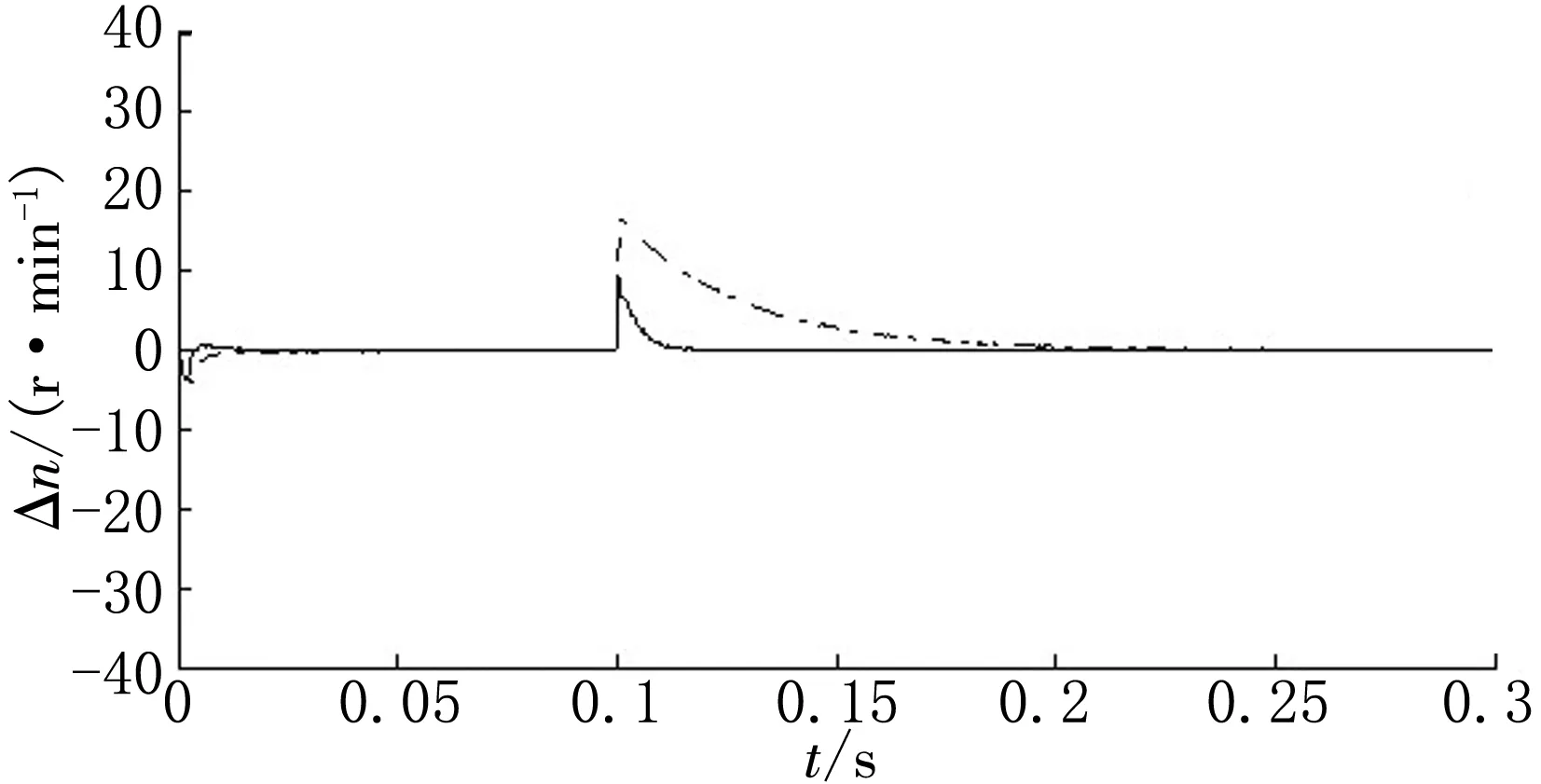
(b)电机2、3同步误差
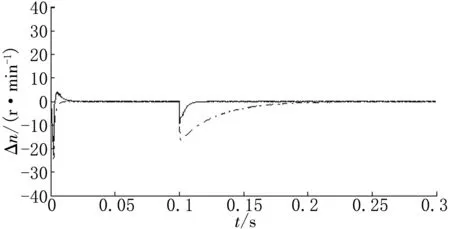
(c)电机3、4同步误差
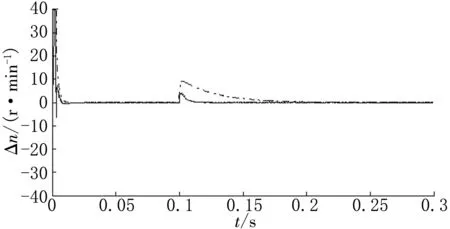
(d)电机4、1同步误差
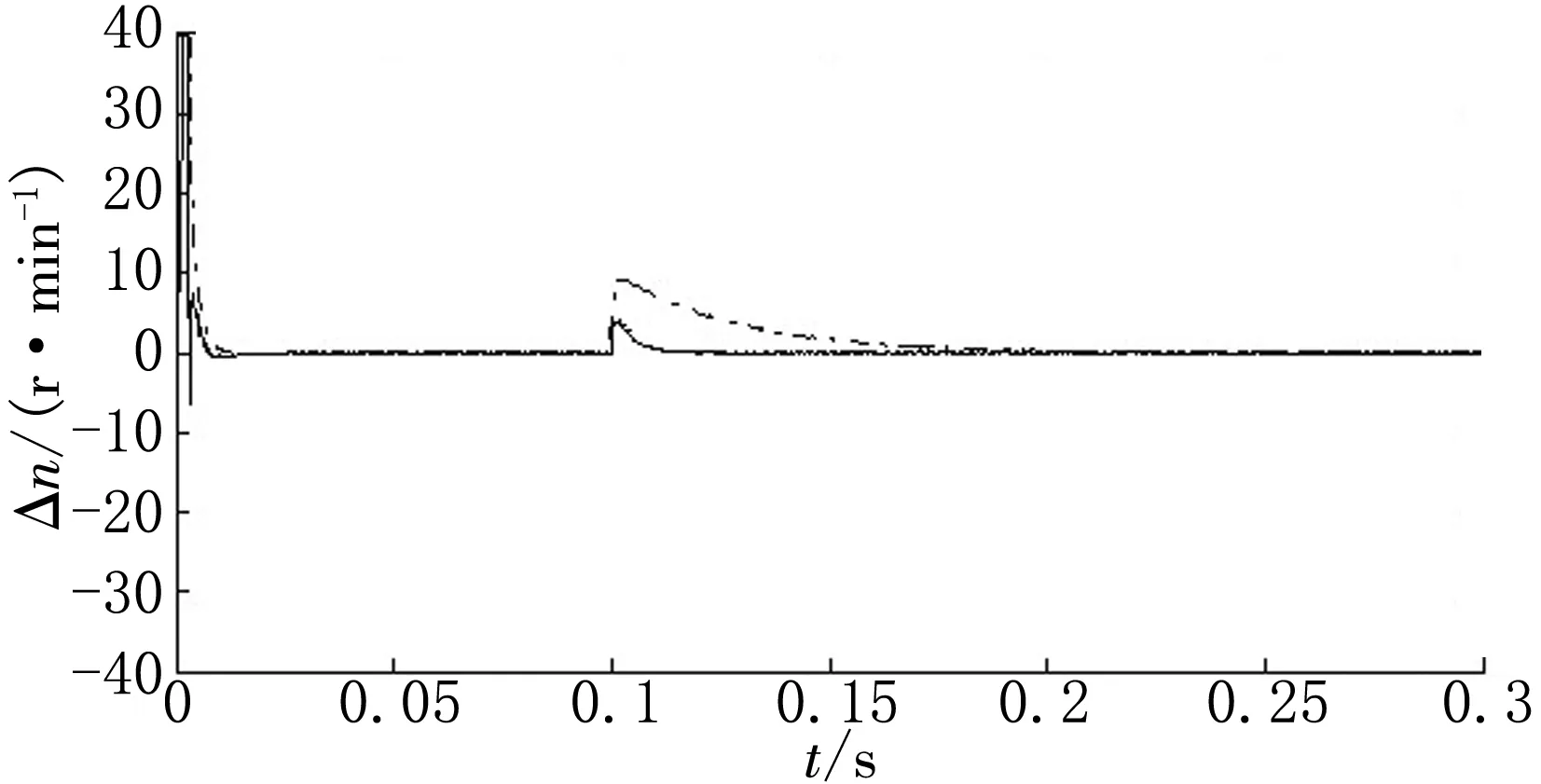
(e)电机1、3同步误差
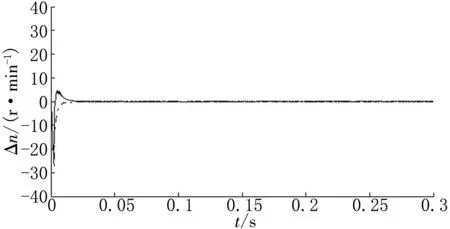
(f)电机2、4同步误差图11 四电机同步误差曲线
5 结语
本文在多电机同步控制系统中采用免疫单神经元PID控制器对速度环进行控制,解决了传统PID控制器不能在线实时调整参数的缺点,有效抑制了负载扰动、电机参数不匹配等因素的影响。仿真对比结果证明了这种算法对多电机同步控制的可行性和有效性,达到了满意的控制效果。
[1] DU H,WEI J H.Motion synchronization control of four multistage cylinders electro-hydraulic elevating system[C] //2010 International Conference on Mechanic Automation and Control Engineering.Wuhan,China:IEEE,2010:5249-5253.
[2] 姜晓平,朱奕,伞冶.大功率随动试验台多永磁同步电机同步控制[J].电机与控制学报,2014,18(4):88-95.
[3] Koren Y.Cross-coupled biaxial computer conerol for manufacturing system[J].ASME Journal of Dynarmic system,Measurement and Control,1980,102(12):265-272.
[4] SHIH YT,CHEN C S,LEE A C.A novel cross-coupling control design for bi-axis motion[J].International Journal of Machine Tool & Manufacture,2002,42(14):1539-1548.
[5] 肖海峰,李凯.改进型相邻耦合误差的多电机同步控制策略[J].自动化与仪器仪表,2014(9):148-151.
[6] Francisco Perez-pinal J,Calderon G.Relative coupling strategy[J].IEEE,2003,2(6):1162-1166.
[7] 彭晓燕,刘威,张强.基于改进型偏差耦合结构的多电机同步控制[J].湖南大学学报,2013,40(11):77-83.
[8] 曹春平,王波,胥小勇,等.基于神经网络多电机偏差耦合同步控制研究[J].控制工程,2013,20(3):415-418.
[9] 王科,刘新正.免疫单神经元PID控制在永磁交流伺服系统中的应用[J].西安交通大学学报,2010,44(4):76-81.
[10] CASTROL N D,TIMMIS J I.Artificial immune systems as a novel soft computing paradigm[J].Soft Computing,2003(7):526-544.
