开放式环境下变电站机器人SLAM算法研究
2018-04-20宋建涛李功燕
任 杰,宋建涛,李功燕,
(1. 中国科学院大学,北京 100049;2. 中国科学院微电子研究所,北京 100029;3.中国科学院物联网研究发展中心,江苏 无锡 214135)
0 引言
为了保证巡检的可靠性与安全性,变电站对于自主巡检机器人的需求日益增大。同时定位与建图(Simultaneous Location and Mapping,SLAM)最先是由Smith和Cheeseman提出的,由于其重要的理论研究以及实际应用价值,被认为是实现机器人自我定位及导航的关键,因此也成为了该领域的研究热点[1]。对于SLAM问题的求解,经历了从卡尔曼滤波,到扩展卡尔曼滤波等延伸算法,最后到粒子滤波的过程[2-6]。卡尔曼滤波因其自身特性,无法有效处理非高斯、非线性情况,而粒子滤波则无此限制。所以,近年来,粒子滤波已经成为了求解SLAM问题的主要方法。
移动机器人SLAM问题的求解总共分为两部分,一部分叫做运动更新,是根据里程计的数据进行更新;另一部分叫做观测更新,是根据传感器数据对运动更新进行矫正,求解最佳位置。根据传感器类型的不同(激光或者摄像头),也分为激光SLAM和视觉SLAM两个方向。其中激光SLAM因为其测量精确、稳定性高、算法成熟,已逐渐应用到变电站巡检等各个领域[7]。
搭载激光传感器的变电站巡检机器人在粒子滤波的基础上,发展出两类比较成熟的算法。第一类是以栅格地图创建(Grid Mapping, GMAPPING)为代表的SLAM算法[8]。此类算法同步性高,将机器人定位与地图构建同时进行,但在实际应用中往往因为计算量过大,难以满足实时性要求,同时因为路径规划等问题难以投入使用。第二类算法是以增强蒙特卡洛定位(Augmented Monte Carlo Localization,AMCL)算法为代表的地图匹配算法[9]。该算法将SLAM问题中的“建图”与“定位”拆分,使用第一类方法构建的地图作为先验知识,只需将激光数据与原地图匹配进行“定位”运算,在静态环境下大大提高了计算效率,减少了资源消耗,达到了实时性与稳定性的要求。但由于过于依赖先验地图知识,一旦地图发生变化,算法的可靠性将大大降低。
变电站一般为开放式的室外环境。变电站机器人的巡检既需要满足实时性的要求,又要机器人在动态环境下仍能保持稳定。本文结合上述两种算法的优缺点,将两种算法融合,提出了一种在原有地图上局部实时建图的算法。该算法的核心思想是:在地图的静态区域仍使用原有AMCL算法,机器人行驶至地图发生变化的区域时使用GMAPPING算法进行局部实时建图,并将新建地图与原地图进行重合,机器人驶出后恢复使用原地图。本文选取地图发生变化的变电站作为实验场地,发现使用原有AMCL算法会出现较大偏差甚至完全丢失位置,而使用局部建图算法则可较好地完成巡检。同时,针对局部建图算法中地图重合和变换关系选取等问题,采用多种策略进行比较,最终选定了最小二乘(Least Square,LS)方法计算变换关系。根据实际测试情况可以看出,局部建图算法融合了两种现有算法的优点,能够较好地解决开放式环境下地图发生变化的问题,是一种有效而实用的方法。
1 基本算法介绍
1.1 GMAPPING算法
GMAPPING算法是一种基于2D激光传感器的算法,其主要作用是构建2D地图。该算法的核心思想是:先随机给定机器人在当前环境中的初始坐标,然后以初始坐标为起点开始建图,该部分建图完成后,机器人移动,将上一时刻新建完成的地图与机器人采集的激光数据进行匹配,从而确定机器人位置,再根据激光相对于机器人的位置完成建图。显然,这是一个递推过程。GMAPPING算法的主要步骤[10]如下:
(1) 输入t-1时刻的里程计信息ut-1,粒子集合St-1,以及t时刻的观测值zt。
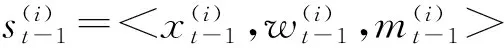
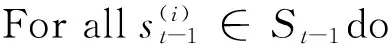
(4) 进行运动更新。结合里程计模型更新粒子位置。
(5) 进行观测更新。用观测模型进行更新,并结合运动更新后粒子位置、上一时刻粒子权值计算当前时刻粒子权值。
(7) 根据观测信息以及计算的最佳粒子位置,更新地图。
(9) End for
(10) 从St中进行重采样。
运动更新以及观测更新等的计算过程本文不展开论述,具体请参照参考文献[10]。
GMAPPING算法的弊端在于,一方面,每个粒子都需要单独维护一幅地图,计算量较大,在大环境下难以满足实时性的需求;另一方面,二维激光所提供的信息仅仅是与激光等高的一个平面,对于路径、路面等信息完全无法估计,造成了路径规划时的困难。因此,虽然GMAPPING算法也自带定位功能,但在实际应用中往往只使用该算法来建图,将得到的地图作为先验知识使用AMCL算法进行定位。
1.2 AMCL算法
AMCL算法也是基于粒子滤波的一种算法,它将SLAM问题中的“建图”与“定位”拆分,使用第一类方法构建的地图作为先验知识,只需将激光数据与原地图匹配进行“定位”运算,在静态环境下大大提高了计算效率,减少了资源消耗,达到了实时性与稳定性的要求。同时,因为有了地图作为先验知识,所有的路径规划均可以地图为基准进行规划,有效避免了GMAPPING算法的弊端。
AMCL算法与GMAPPING算法的步骤大致相同,不同点在于:
(1) 因为AMCL不用进行地图构建,所需计算量大大减小,所以在进行粒子滤波时可以大量增加粒子数量来提高精度(通常可以达到几百或几千)。
(2) 因为粒子数目大量增加,小范围内粒子位置可基本覆盖正确位置,在进行当前时刻位置计算时可以不用计算高斯分布,直接用最佳粒子位置代替机器人位置。
AMCL算法的弊端在于,需要地图作为先验知识,一旦地图发生变化,算法的可靠性将大大降低。所以,在变电站这种开放式的大环境下,长时间使用AMCL算法仍会出现一些问题。因此,提出了局部建图算法。
2 局部建图算法
局部建图算法的核心思想是:在地图的静态区域仍使用原有AMCL算法,机器人行驶至地图发生变化的区域时使用GMAPPING算法进行局部实时建图,并将新建地图与原地图进行重合,机器人驶出后恢复使用原地图。它融合了GMAPPING算法与AMCL算法的优点,既实现了较为方便的路径规划,又满足了实时建图的需求。
2.1 算法分析
局部建图算法的关键点在于如何实现新建地图与原地图的重合。新建地图后,机器人所获得的自身坐标是相对于新图的坐标,只有将这个坐标转换到旧图坐标上才能保证之前设定的路径规划等功能不受影响。

但是,另一方面,由于激光传感器误差、算法本身误差等原因,“切换点”的坐标不一定是完全准确的,尤其是此时的机器人朝向R(单位为°),一旦与真实朝向有一个偏差角r,那么新建地图与原有地图也将有一个r角度的偏差。这个偏差带来的误差可以用式(1)表示:
Δσ=sinr
(1)
即偏离1°误差就可以达到1.74%,对于50 m误差可以达到87 cm,这是实际应用中无法接受的。

该算法的主要误差分为两类,一类是算法本身的误差,包括模型误差、噪声误差、传感器导致的误差等,通常这些误差较小;另一类是切换后变换关系导致的误差,根据之前叙述,该算法对角度的敏感度非常高,虽然采取了一定的方法去解决,但是仍会出现不可避免的误差。第二类误差的量与机器人行驶距离成正比,是线性误差。
2.2 算法步骤
局部建图算法的主要步骤如下:
(1) 在地图无变化区域使用原有AMCL算法。
(2) 选择切换点,经过切换点后进入学习阶段。
(3) 学习阶段开启GMAPPING建图,但不输出机器人位置,同时不关闭AMCL算法,将AMCL算法得到的机器人位置作为输入给GMAPPING。用LS方法计算两种坐标间的转换关系,得到关联式。
(4) 关闭AMCL算法,同时开启GMAPPING输出,利用关联式将新输出坐标转换到旧地图上。
(5) 驶出地图变化区域,将得到的坐标作为初始位置送给AMCL算法,同时关闭建图与GMAPPING的位置输出。
3 实验检验
根据第2节介绍,该算法的第一类误差较小,通常为几厘米,第二类误差呈线性,在行驶距离较大时误差较大。因此,在行驶距离较大时,该算法的整体误差大致呈线性。可以通过测量机器人行驶一定距离后偏离正常位置的距离来验证算法的可靠性。
本文使用杭州申昊科技股份有限公司生产的SHIR-3000X型机器人,搭载西科公司生产的LMS511型激光。该机器人已经在浙江、湖北等地的多个变电站中投入使用。实验场地是浙江金华明珠变电站,该实验场地早在建设的过程中就对机器人应处的正确位置做出了标定。选择的实验路段总长度为50 m、宽度为2 m。
该实验场地因为道路两旁绿化带生长,现场环境与先验地图有较大偏差,机器人在正常巡检过程中时常出现无法找到正确位置的情况,图1是10次实验中,机器人偏离正常位置的最大距离D。其中方块代表使用AMCL算法,圆代表使用没有学习阶段的局部建图算法。误差达到1 m表示机器人丢失自身位置。
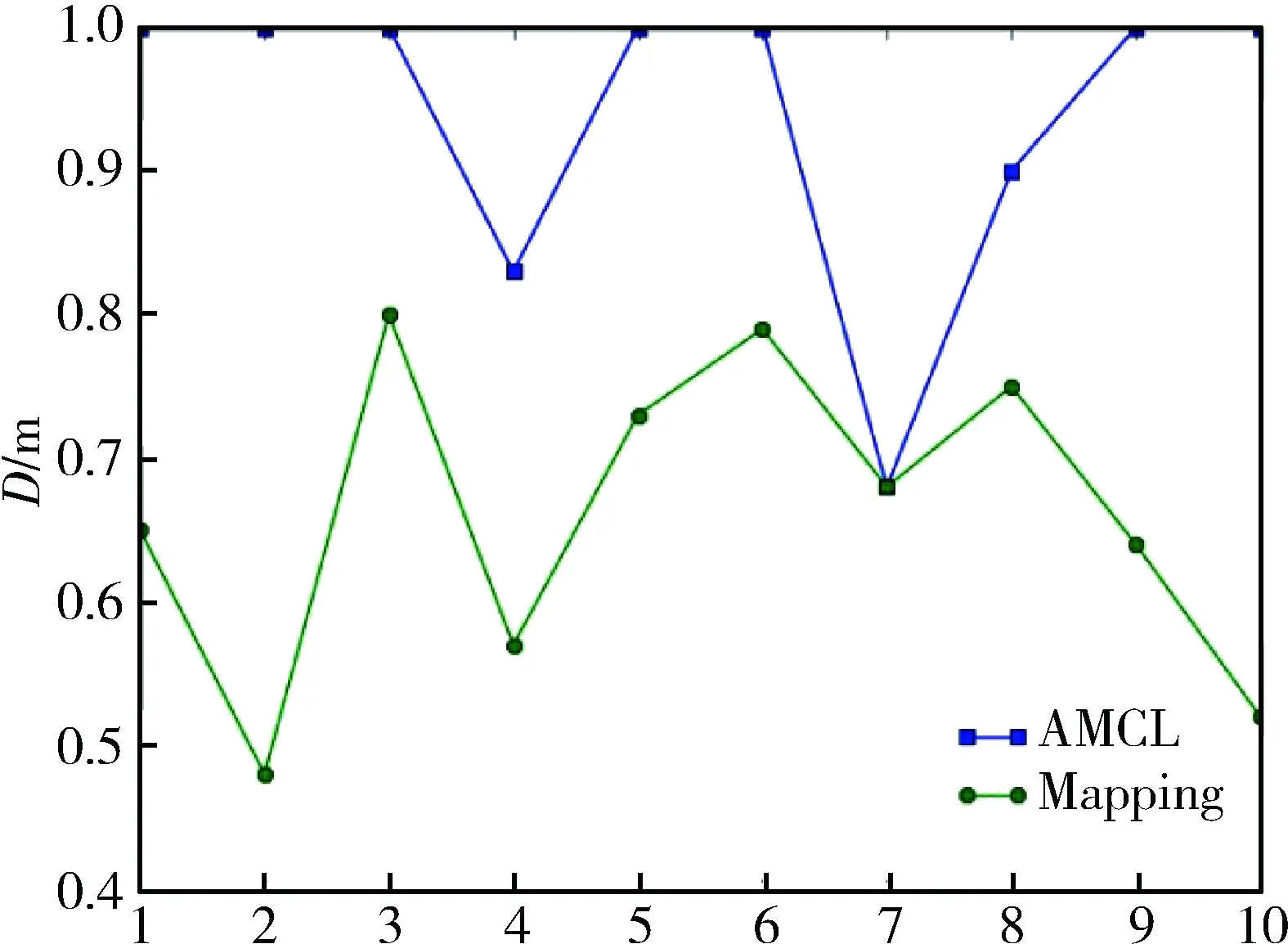
图1 10次实验机器人偏离正常位置最大距离
由图1可以看出,在使用AMCL算法的情况下有7次机器人完全丢失位置,3次没有丢失位置的情况也都出现了较大偏差。而使用局部建图算法10次都完成了50 m的路程,但是在不搭建学习区域的情况下,最大误差可以达到80 cm,难以满足要求。可以看出,局部建图算法能够满足适应变化环境的要求,但在精度方面仍需提升。
图2是采用不同的精度提升策略得到的行驶距离与误差关系图。X轴表示的是机器人行驶距离L,Y轴表示的是10次实验下的平均偏差D。方块代表的是不使用任何策略;圆点代表使用学习区域,但不用LS算法处理,而是计算相应坐标间的变换关系然后求平均;三角代表使用LS方法求解关联式。
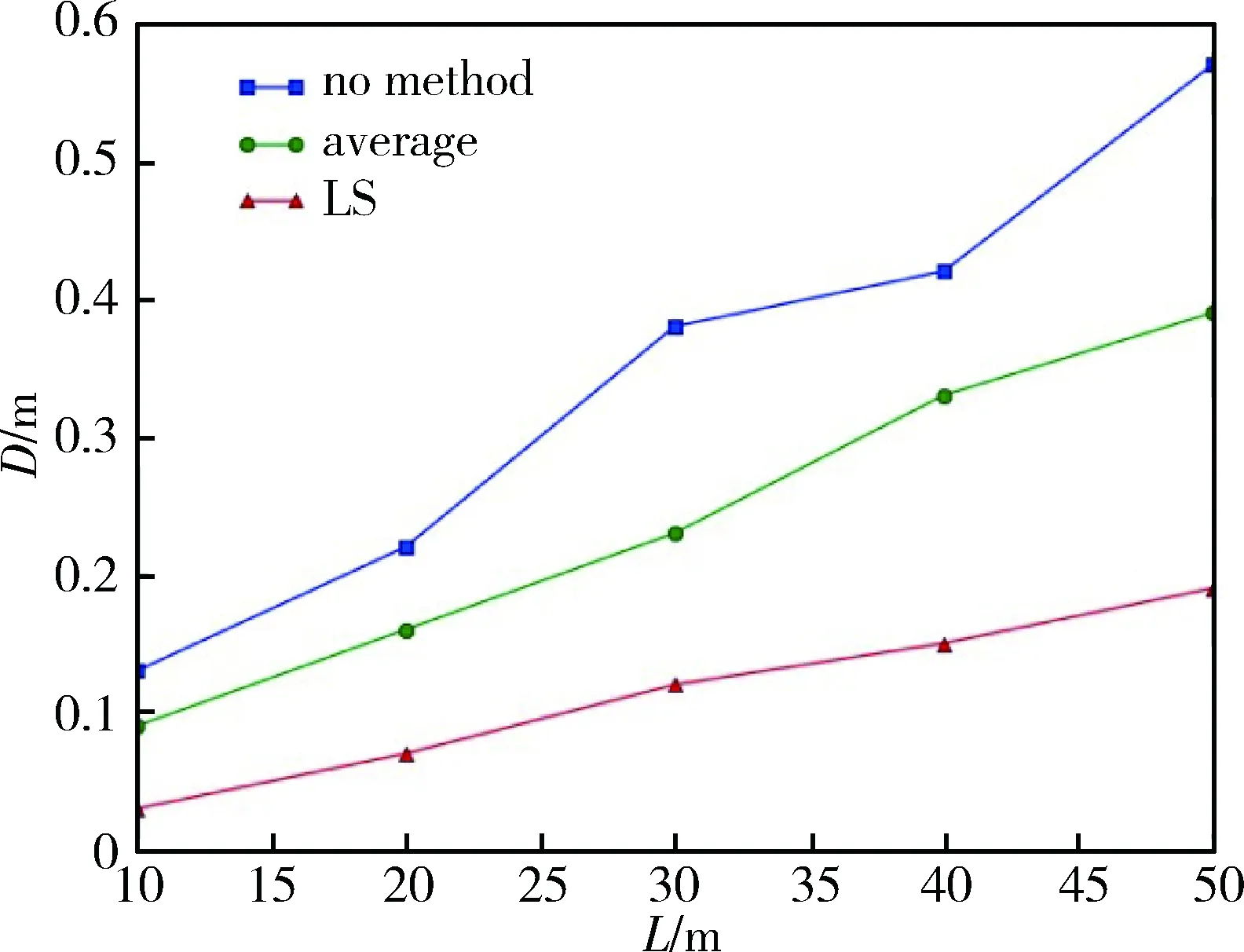
图2 机器人行驶距离与平均偏差图
由图2可以看出,10次实验下的偏差呈近似的线性分布,采用两种策略均能极大改善起始点选择带来的偏差,其中使用LS方法可以把误差控制在20 cm内,能够满足现场使用需求。根据实验,最终选择使用LS方法求取关联式来提高算法精度。
4 结论
本文针对传统二维激光SLAM算法实时性差、对先验地图过于依赖的弊端,提出了一种能够在开放式环境下使用的局部建图算法。该算法在地图无变化区域使用原有算法,在地图变化部分实时局部建图,并与原地图重合。通过与传统AMCL算法的比较,证明了该算法能够较好地解决现场环境发生变化与先验地图产生偏差的情况。同时通过实验验证,证明了使用LS方法建立关联式,能够有效地解决算法精度问题。但该算法的误差与机器人行驶距离成正比,在长距离中只能进行分段使用。分段使用过程中,如何在进出时快速收敛自身位置是以后的研究方向。
[1] WILLIAMS S B. Constrained initialization of the simulataneous localization and mapping algorithm[J].International Journal of Robotics Research,2003,22(7/8):541-564.
[2] WELCH G, BISHOP G. An introduction to the Kalman filter[M]. University of North Carolina at Chapel Hill, 2006.
[3] SHOUDONG H, GAMINI D. Convergence and consistency analysis for extended Kalman filter based SLAM[J]. IEEE Transactions on Robotics,2007(5):1036-1049.
[4] ADAMS M, ZHANG S, XIE L. Particle filter based outdoor robot localization using natural features extracted from laser scanners[C]// IEEE International Conference on Robotics and Automation, 2004:1493-1498.
[5] LUBIN C, BAIQING H, AN L. Transformed unscented Kalman filter[J]. IEEE Transactions on Automatic Control, 2013(1):252-257.
[6] DOUCET A, DE FREITAS N, MURPHY K, et al. Rao-Blackwellised particle filtering for dynamic Bayesian networks[C]//Proceedings of the Sixteenth Conference on Uncertainty in Artificial Intelligence. Morgan Kaufmann Publishers Inc., 2000: 176-183.
[7] 李红梅, 王滨海, 廖文龙,等. 基于地图匹配的变电站巡检机器人激光导航系统设计[J]. 制造业自动化, 2014(1):52-56.
[8] GRISETTI G,STACHNISS C, BURGARD W.Improving Grid-based SLAM with Rao-Blackwellized particle filters by adaptive proposals and selective resampling[C]//Proceedings of the 2005 IEEE International Conference on Robotics and Automation,2005:2432-2437.
[9] DELLAERT F,FOX D,BURGARD W,et al,Monte Carlo localization for mobile robots[C]//Proceedings 1999 IEEE International Conference on Robotics and Automation (Cat. No.99CH36288C), 1999:1322-1328.
[10] GRISETTI G,STACHNISS C, BURGARD W.Improved techniques for grid mapping with Rao-Blackwellized particle filters[J].IEEE Transactions on Robotics, 2007(1):34-46.
[11] 赵景堂,杜国明,李秀海.基于总体最小二乘法的二维坐标转换方法[J].黑龙江工程学院学报,2015(1):21-22.
