基于SVM的建筑电气系统无中心故障诊断算法研究*

赵雪辰，邢建春，王　平，李国平

(中国人民解放军陆军工程大学 国防工程学院，江苏 南京 210007)

0　引言

现如今，现代建筑已越来越向着自动化、智能化的方向发展。但同时也带来许多问题，比如跨子系统集成困难，协议不兼容，需要人工对几万个底层信息点和传感器进行校对，浪费大量人力物力等，也就是说现代建筑并不那么“智能”。为了较好地解决上述问题，清华大学建筑节能研究中心提出了构建一种建筑无中心智能控制系统的想法[1-2]，将建筑的基本单元设置为建筑空间和各种机电设备，并对每个基本单元配置一个独立的计算和通信处理设备，称为计算处理节点(Computing Process Node,CPN)。无中心的建筑智能化平台具备节点即插即用、容易扩展、节点之间独立平等的优点，大大减少了人工校对等繁琐的工作，使建筑更趋于自动化、智能化。

建筑电气系统一直以来都是建筑中重要的组成部分，它主要是指供配电系统，越来越复杂的建筑电气系统导致其发生故障的概率大大增加。建筑电气系统一旦发生故障，轻则停电检修，重则引起电气设备损坏，甚至导致火灾事故的发生。

现阶段集中式建筑智能化系统下的建筑电气系统故障恢复效率较低。所以，为了让建筑更加“智能”，就需要让建筑智能化系统在运行过程中自动识别出所发生的故障。

目前，在集中式建筑智能化系统下的建筑电气故障诊断已经有了许多研究成果[3-6]。文献[3]针对实际建筑物中典型样本数据获取困难这一问题，利用支持向量机(SVM)的方法建立建筑电气系统故障仿真模型，并在建筑电气系统故障模拟硬件实验平台上进行了实验，将其结果与人工神经网络的仿真结果进行对比。对比结果表明，SVM的方法在样本数据较小的情况下具备更好的诊断效果。

文献[4]提出一种人工鱼群算法和SVM相融合的建筑电气故障识别模型。采用人工鱼群算法找到最优特征子集，减少分类器维数，融合SVM的方法建立建筑电气故障识别模型，并进行了仿真实验。

由于之前提到集中式建筑智能化系统存在诸多问题，因此在无中心、扁平化的建筑智能化平台下进行建筑电气故障诊断研究就显得很有意义。本文主要基于无中心的建筑智能化平台提出一种基于SVM的故障诊断算法，并在实际配电网拓扑结构下进行仿真分析。该算法主要依靠智能节点之间的数据互传，自组织地对建筑配电网拓扑结构进行故障诊断，在诊断过程中不需要集中式的监控主机，诊断效果以及诊断速度都有了较大的提升。

1　基于SVM的建筑电气故障诊断理论

SVM是建立在统计学习的VC维理论和结构风险最小原理基础上的一种数据挖掘方法，目前已经较为成熟地运用在模式识别、预测分析等领域[7-11]。

SVM核心思想是找到一个最优超平面使两类样本到该平面的间隔最大，本文节点所插入的SVM采取二分类的策略。假设有两类数据样本，给定训练样本集(xi,yi),i=1,2,…,l,x∈Rn,y∈{±1}，将分类的超平面记为(w·x)+b=0，为了使样本正确分类且分类间隔最大，就必须满足：

yi[(w·xi)+b]≥1,i=1,2,…,l

(1)

(2)

为了解决这个最优化问题，引入Lagrange函数：

(3)

式中，ai为拉格朗日系数。上述最优化问题满足对w和b的偏导为零，将该问题转化为相应的对偶问题：

(4)

得到最优的拉格朗日常数之后，再利用偏导为零，求出最优权向量w*和最优偏置b*：

(5)

(6)

建筑电气故障诊断问题实质上就是一个分类问题，建立其故障诊断模型，将该故障诊断问题转化为带约束条件的优化问题来求解，其数学模型一般为：

s.t.g(x)≤0,h(x)=0

(7)

求解该带约束条件的方法为将相邻节点的共有变量解耦，加入一个惩罚函数α，将上述数学模型转化为[6]：

s.t.gi(xi)≤0,hi(xi)=0

(8)

其中xij,i,xij,j表示节点i、j共有的变量。

建筑电气系统故障诊断问题就是一个将故障数据从正常数据中剔除出来的过程，即将故障状态与正常状态进行分类识别。而SVM就是寻找一个最优的超平面将两类样本很好地分隔开，并且建筑电气系统的数据量相较于其他的电力系统来说较小，采用SVM能较好地解决小样本情况下的分类问题。本文所用算法中节点的SVM采用二分类的策略，将故障状态的SVM输出值设为-1，正常状态的SVM输出值设为1。在不同的智能节点上独立地运行训练好的SVM，通过邻居节点之间的数据互传以及最终的SVM输出值来判断节点的状态。

2　基于SVM故障诊断的无中心算法

集中式的SVM主要解决如下式所示问题：

(9)

考虑一个实际建筑配电网的拓扑结构，给定每个智能节点的训练集Sj={(xjn,yj)，n=1,2,…,Nj},其中，yjn∈{1,-1},j=1,2,…,J,J代表拓扑结构中智能节点的个数，Nj代表每个智能节点的样本数。

无中心算法要求每个节点与邻居节点进行数据互传，将邻居节点的数据作为本地节点的样本属性值，即本地节点的训练集变为Sj={(xjn,yj)，n=1,2,…,Njk}，Njk代表本地节点本身的数据样本以及从邻居节点收取过来的数据样本[12-13]。则将原先集中式的SVM无中心化，同时加入一个节点之间的一致性约束wi=wj,bi=bj，便可得到如下的无中心化SVM模型：

(10)

ζjn≥0,∀j∈J,n=1,2,…,Njk

wj=wi,bj=bi,∀j∈J,i∈Bj

式中，C>0为加入的惩罚因子，ξ为当样本为线性不可分时加入的松弛因子。

本文所提出的无中心自识别算法没有集中式的故障诊断模型，在每个节点上都插入一个SVM，仅靠邻居节点互传数据来判断节点的正常与否，如上式所示，将整个全局的故障诊断问题分解为在每个智能节点上的局部问题，分布式地进行求解。算法步骤如下：

(1)本地节点收取自身样本数据xjn，并将自己的数据传递给邻居节点，同时本地节点收取邻居节点的样本数据xkn。

(2)将本地节点的样本数据xjn以及邻居节点的样本数据xkn作为每个节点SVM的属性值，采集正常状态下的数据以及每个节点故障状态下的数据作为SVM的训练样本。代入到式(10)中求出每个智能节点的最优超平面，将此平面作为无中心建筑智能化平台正常运行之后的分类依据。

(3)SVM采取二分类的策略，将正常状态下各节点SVM输出值均设为1。当某一节点发生故障时，将故障节点的SVM输出值设为-1，其余节点的SVM输出仍为1。按照上述策略以及采集到的正常状态和故障状态的数据对各节点SVM进行训练。

SVM采取二分类主要是将其中的故障数据分离出来，每个节点上所存放的数据为:[xj1,xj2,…,xjk;yj]，正常数据下的yj=1，故障数据则为yj=-1。

(4)在每个节点独立地运行训练好的SVM，节点之间互传数据进行迭代计算。当某节点的SVM输出为-1时，则该节点发生故障。图1为每个时刻节点之间的同步迭代示意图。

图1同步迭代示意图

将上述算法嵌入到每一个智能节点中，对于每个节点来说，嵌入的算法都是完全一样的，该算法具有以下优点：

(1)简单易行。算法只需要相邻节点之间数据互传，并将训练好的SVM输入到智能节点中去，不必在中央节点上建立全局的故障诊断模型，并且该算法适用于大多数拓扑结构。

(2)并行计算。该算法多个节点并行地进行计算，加快了处理速度，提高了运算效率。

需要特别进行说明的是，该算法只能自组织地识别出发生故障的智能节点，并不能估计此故障的严重程度。根据算法得到的结果，首先得出具体哪个节点发生故障，然后再根据智能节点之间存在的一些物理约束关系来判断此节点故障的严重程度。

3　仿真实验与分析

以图2所示实际建筑配电网结构为例对算法进行仿真验证。将每个母线当成一个智能节点，利用电源管理单元(Power Management Unit，PMU)测量装置对母线电流、电压数据进行采集。其智能节点的网络拓扑图如图3所示。首先采集正常状态以及每个节点故障时的数据对各个节点的SVM进行训练，然后将训练好的SVM插入到每个节点中去，观察各个节点的SVM输出值，进而自组织地识别出故障位置。

图2　建筑配电网实际结构图

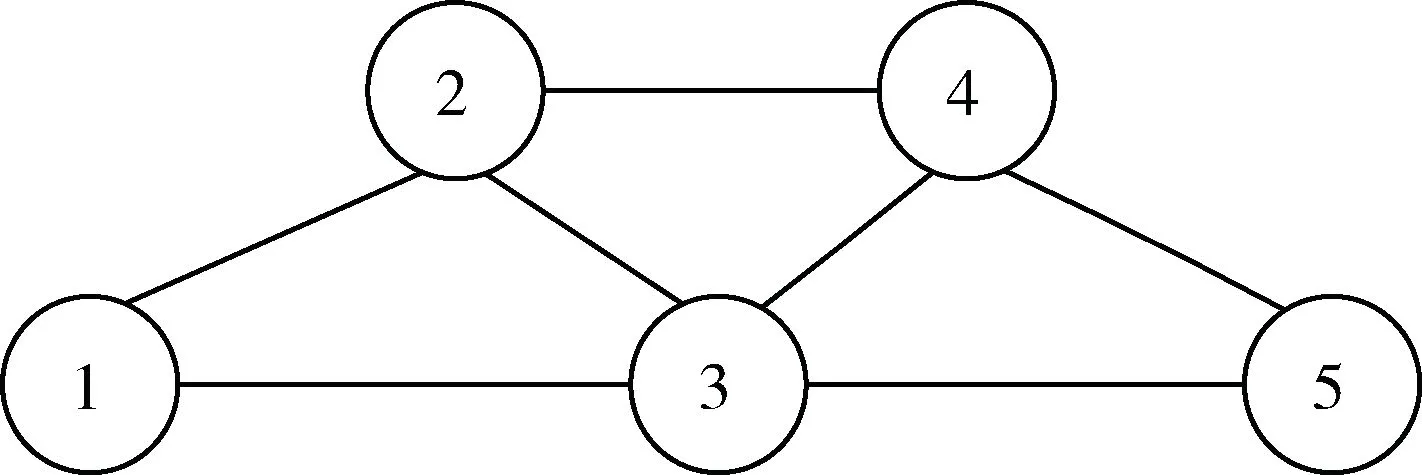
图3　智能节点网络拓扑结构图

(1)单个节点(以节点1为例)故障

在各个节点上分布式并行地运行质量因素的情况下，当采样时刻结束时SVM输出值为-1的节点即为故障节点。图4中各子图分别为各节点的SVM输出值的变化过程。

(2)两个节点(以节点2、5为例)发生故障

当两个或两个以上节点发生故障时，由于所选拓扑结构节点均为相邻节点，训练的过程会比较复杂。假设在时刻4发生故障，观察各节点SVM的输出值。图5中各子图分别为各节点故障检测的结果图。

(3)三个节点(以节点1、3、4为例)发生故障

同样地，在每个智能节点上运行基于SVM的无中心故障诊断算法，对10个时刻的测量值进行采集，观察各节点SVM的输出值。图6中各子图分别为各节点SVM输出值示意图。

图4　单个节点故障检测结果

图5　两个节点故障检测结果

图6　三个节点故障检测结果

4　结论

针对扁平化、无中心建筑智能化系统提出的基于SVM的建筑电气故障无中心算法具有以下特点：

(1)实时性。无中心算法将训练好的SVM插入到每个节点中，通过节点之间当前时刻的数据互传进行并行运算来对节点的状态进行诊断，运算速度快，克服了一般算法的滞后性。

(2)普适性。无中心算法不是只针对某些特定的配电网结构，只要对每个节点的SVM训练完成，插入到节点中即可达到诊断效果。

(3)并行性。无中心算法要求多个节点同时参与并行计算，运算速度较快。

本文提出了一种基于无中心智能化平台的建筑电气系统故障诊断算法，但该算法才刚刚起步，无中心故障诊断算法在系统规模较大的情况下比集中式算法运用更为灵活。如何将无中心算法推广到实际的无中心智能化建筑中，是下一步非常有意义的研究工作。

[1] 沈启. 智能建筑无中心平台架构研究[D]. 北京：清华大学, 2015.

[2] 代允闯.空调冷冻站“无中心控制系统”研究[D]. 北京：清华大学,2016.

[3] 张龙. 建筑电气系统故障诊断方法研究[D]. 北京：北京林业大学, 2014.

[4] 李忠. 人工鱼群算法和支持向量机的建筑电气故障识别[J]. 电气应用, 2015(16):89-93.

[5] CHEN F, WANG Y, SHEN L, et al. The design of the building electrical fault diagnosis system based on multi-agent[C]// Control and Decision Conference. IEEE, 2015:3345-3349.

[6] WU Q, WANG Y, ZHANG L, et al. The research on fault diagnosis of building electrical system based on RBF neural network[C]// Proceedings of 2013 Chinese Intelligent Automation Conference. Springer Berlin Heidelberg, 2013:9-19.

[7] CRISTIANINI N，TAYLOR J S. 支持向量机导论[M]. 李国政，王猛，曾华军，译.北京：电子工业出版社, 2004.

[8] 张学工.关于统计学习理论与支持向量机[J]. 自动化学报, 2000, 26(1):32-42.

[9] STOLPE M, BHADURI K, DAS K. Distributed support vector machines: an overview[M].Solving Large Scale Learning Tasks. Challenges and Algorithms. Springer International Publishing, 2016.

[10] FLOURI K, Beferull-LOZANO B, TSAKALIDES P. Distributed consensus algorithms for SVM training in wireless sensor networks[C]// Signal Processing Conference, 2008, European. IEEE, 2008:1-5.

[11] 虞国全. 基于支持向量机的智能故障诊断技术研究[D]. 南昌：南昌大学, 2007.

[12] 王世强, 姜子炎, 邢建春,等. 空调系统传感器故障检测的无中心算法[J]. 制冷学报, 2016, 37(2):30-37.

[13] 王世强, 邢建春, 李决龙,等. 一种传感器故障诊断的无中心自组织算法[J]. 微电子学与计算机, 2016, 33(5):80-84.