河湖堤坝在地震作用下稳定性计算分析

邹　凯，袁宝远，肖　衍

(河海大学地球科学与工程学院，南京　211100)

堤坝决堤是河湖近岸地区可能遇到的重要灾害。我国东部是河湖堤坝工程高密度存在区域，洪水期一旦出现河湖堤坝溃决，不仅国民经济受到重大损失，而且危及广大人民的生命财产。工程技术人员对堤坝在河湖水位影响下堤坝稳定性[1]及渗透稳定性[2]比较重视，在地震作用下比较关心地震液化[3]现象,但对河湖堤坝在地震作用下的稳定性重视不够。与河湖堤坝相关的土石坝工程[4]、尾矿坝工程[5]及边坡工程[6],在地震作用下的稳定性分析方法主要为有极限平衡分析法[7]、地震拟静力数值分析法[8]和地震动力数值分析法[9]。这些方法对堤坝地震稳定性计算分析具有很好参考价值。

江苏境内的京杭大运河，分为苏北、苏南运河。苏北运河全长404km，沟通了微山湖、骆马湖、洪泽湖、高邮湖等水系，是京杭运河上运输最繁忙的河段，基本建成二级航道，成为京杭运河上等级最高的航道。其中扬州段在公元前486a开筑，公元前175a形成运盐河，是隋唐大运河、京杭大运河的一部分，历经多次疏浚、整治，也是河面最宽、河床最深的河段。其中的高邮城区临近高邮湖，1931a夏淮河流域暴雨连绵，洪水期间运河大堤26处先后决堤，高邮及里下河各县尽成泽国，死亡7.7万余人，受灾350万余人。京杭运河扬州段地理位置重要，运河大堤的安全极其重要，地震作用会明显降低运河大堤的稳定性，进行地震安全性分析评价意义重大。

1　堤坝模型及极限平衡分析法计算

选用的典型剖面位于京杭运河扬州段高邮城区，堤坝顶高程为12.5m，坝顶宽度为8m，洪水位9.5m，堤外地面高程5.5m,河床高程2m，地面水位5.5m，临河坡度23°，临地坡度23°。

选用Geo-Studio SLOPE/W分析软件进行极限平衡计算，根据室内试验结果，坝体材料内聚力38.8kPa，内摩擦角22.1°，可塑黏土层内聚力35.4kPa，内摩擦角14.6°，硬塑黏土层内聚力31.7kPa，内摩擦角22.1°。考虑地震拟静力荷载，加速度峰值：基本地震动(50a超越概率10%)为0.125g，罕遇地震动(50a超越概率2%)为0.212g，罕遇地震动(100a超越概率2%)为0.250g。

图1是模型剖面及基本地震动(50a超越概率10%)工况用极限平衡法中的Janbu法计算得出的稳定系数结果图。

表1是模型在各种工况下，利用Ordinary、Bishop、Janbu及Morgenstern-Price等极限平衡计算方法，在向河流方向和向地面方向滑动的计算稳定性系数值。

2　地震拟静力数值分析法计算

选用FLAC3D数值分析软件进行地震拟静力数值分析计算，计算参数由室内常规试验获得，见表2。根据《建筑边坡工程技术规范》GB 50330-2013规定，地震拟静力荷载峰值加速度计算时乘0.25系数，拟静力加速度：基本地震动(50a超越概率10%)为0.031 25g，罕遇地震动(50a超越概率2%)为0.050 3g，罕遇地震动(100a超越概率2%)为0.062 5g。

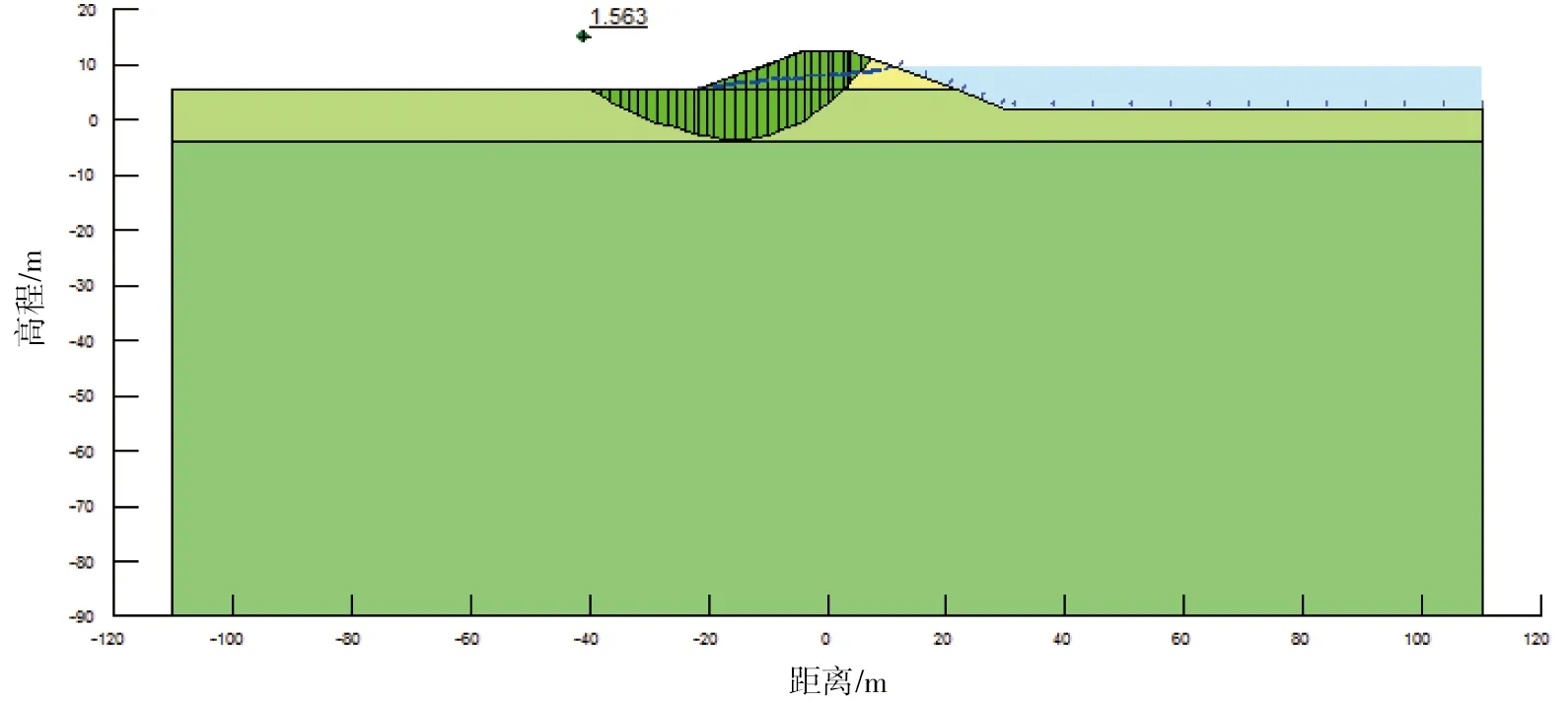
图1　模型50a超越概率10%工况Janbu法结果Figure 1　Janbu method result of model with 50a exceedance probability 10% mode

极限平衡算方法OrdinaryBishopJanbuMorgenstern-Price滑动方向向河向地向河向地向河向地向河向地天然工况2.7212.53.1482.7572.6452.3622.942.638基本地震动(50a超越概率10%)1.7351.6752.0351.9881.5791.5631.7791.755罕遇地震动(50a超越概率2%)2.0251.2592.1781.9961.2341.2241.3181.312罕遇地震动(100a超越概率2%)1.5211.1411.8721.7931.0511.0701.1181.148

表2　地震静力计算材料参数

计算重力加水压力再加地震静力作用工况，计算在某些强度折减系数时的地震静力作用，对比分析各模型的稳定性。

利用数值分析法计算地震静力作用，在模型中加水平地震静力，加载方向不同结果不同，分为负向(向河方向)和正向(向地方向)。图2是型在重力加水压力负向加50a超越概率10%地震静力折减系数0.6的剪应变增量分布图，显示塑性区已明显贯通。图3是模型在重力加水压力正向加50a超越概率10%地震静力折减系数1.0的剪应变增量分布图，显示塑性区已明显贯通。图4是模型在重力加水压力负向加50a超越概率2%的地震静力折减系数0.3的剪应变增量分布图，显示塑性区已形成规模。

图5是模型在重力加水压力负向加100a超越概率2%的地震静力折减系数0.1的剪应变增量分布图，显示塑性区已形成规模。

从地震拟静力数值分析得出：在基本地震动工况临界强度折减系数为0.6～0.7、罕遇地震动(50a超越概率2%)临界强度折减系数为0.3～0.4，罕遇地震动(100a超越概率2%)工况临界强度折减系数为0.1～0.2。

图2　负向50a超越概率10%静力折减系数0.6剪应变Figure 2　Shear strain diagram of model with negative direction 50a exceedance probability 10% and static reduction factor 0.6

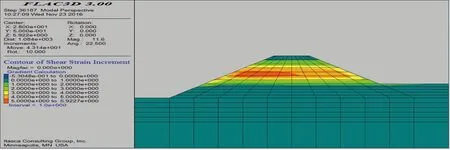
图3　正向50a超越概率10%静力折减系数1.0剪应变Figure 3　Shear strain diagram of model with positive direction 50a exceedance probability 10% and static reduction factor 1.0

图4　负向50a超越概率2%静力折减系数0.3剪应变Figure 4　Shear strain diagram of model with negative direction 50a exceedance probability 2% and static reduction factor 0.3

图5　负向100a超越概率2%静力折减系数0.1剪应变Figure 5　Shear strain diagram of model with negative direction 100a exceedance probability 2% and static reduction factor 0.1

3　地震动力数值分析法计算

选用FLAC3D数值分析软件进行地震动力数值分析计算，动力分析计算材料参数动三轴试验获得，见表3，材料4为便于动荷载计算加的辅助硬性层。

动力分析中采用滞后阻尼形式，阻尼参数由自振柱试验得到的阻尼比曲线确定，地震动力荷载以水平加速度人造波方式，从模型底部施加，作用时长40s。图6为50a超越概率10%人造波加速度时程线。计算重力加水压力再加地震动力作用工况，计算在某些强度折减系数时的地震动力作用。

利用数值分析法计算地震动力作用也是利用强度折减法。图7、图8是模型在50a超越概率10%地震动力作用折减系数0.8、0.7的剪应变分布图，图中显示塑性区已形成规模。图9是模型在50a超越概率2%地震动力作用折减系数0.5的剪应变分布图，塑性区已形成规模。图10是模型在100a超越概率2%地震动力作用折减系数0.4的剪应变分布图，显示塑性区已形成规模。

对于基本地震动(50a超越概率10%)工况，根据模型强度折减系数的计算结果，可以判断该工况下模型的临界强度折减系数为0.6～0.7。对于罕遇地震动(50a超越概率2%)工况， 判断该工况下模型的临界强度折减系数为0.6～0.5。对于罕遇地震动(100a超越概率2%)工况，判断该工况下模型的临界强度折减系数为0.5～0.4。

表3　地震动力计算材料参数

图6　50a超越概率10%人造波加速度时程线Figure 6　Model with 50a exceedance probability 10% artificial wave acceleration time line

图7　模型50a超越概率10%折减系数0.8的剪应变Figure 7　Shear strain diagram of model with 50a exceedance probability 10% and reduction factor 0.8

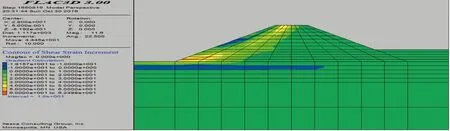
图8　模型50a超越概率10%折减系数0.7的剪应变Figure 8　Shear strain diagram of model with 50a exceedance probability 10% and reduction factor 0.7

图9　模型50a超越概率2%折减系数0.5的剪应变Figure 9　Shear strain diagram of model with 50a exceedance probability 2% and reduction factor 0.5

图10　模型100a超越概率2%折减系数0.4的剪应变Figure 10　Shear strain diagram of model with 100a exceedance probability 2% and reduction factor 0.4

4　计算结果综合分析

根据极限平衡法计算的模型堤坝稳定性系数基本地震动工况最低为1.563，大于稳定性安全系数1.35；罕遇地震动(50a超越概率2%)稳定性安全系数最低为1.224，大于稳定性安全系数1.15；罕遇地震动(100a超越概率2%)工况下模型小于于稳定性安全系数最低为1.051，大于1.0。极限平衡法施加的是地震静力，并且地震静力单向加载，地震静力只加在潜在滑体内。没有考虑滑体外的地震静力作用是该计算方法的主要缺点，所以利用极限平衡法计算地震静力作用稳定性系数明显偏高。

利用FLAC3D数值计算地震静力作用，堤坝稳定性系数在基本地震动工况临界强度折减系数为0.6～0.7、罕遇地震动(50a超越概率2%)临界强度折减系数为0.3～0.4，罕遇地震动(100a超越概率2%)工况临界强度折减系数为0.1～0.2。模型的计算稳定性明显偏低，特别是罕遇地震动工况，其原因，主要是按静力方法施加地震荷载与实际情况有一定差别，特别就是单向加载。

利用FLAC3D数值计算地震动力作用，对于基本地震动工况，临界强度折减系数为0.6～0.7。对于罕遇地震动(50a超越概率2%)工况，临界强度折减系数为0.5～0.6。对于罕遇地震动(100a超越概率2%)工况，临界强度折减系数为0.4～0.5。利用FLAC3D数值计算地震动力作用结果稳定性较低的原因，是坝体土和可塑性黏性土的动抗剪强度比静抗剪强度参数明显小。

综合以上分析，在天然工况下堤坝稳定性状态良好，在基本地震动工况处于明显不稳定状态，可能出现明显局部塑性破坏、罕遇地震动工况下处于严重不稳定状态，可能会出现垮塌性破坏。但所有计算都是施加的水平向地震荷载，当实际地震时主要加速度方向与水平方向不一致时，地震的破坏作用会有所减缓。

5　结论

1)扬州段典型堤坝剖面地震作用下的极限平衡分析法、地震拟静力数值分析法和地震动力数值分析法计算的稳定性结果差异很大。

2)极限平衡分析法一般是Janbu稳定系数数值最小，没有考虑滑体外的地震静力作用是该计算方法的主要缺点，所以稳定性系数明显偏高。

3)利用数值分析法计算地震静力作用，由于单向加载会使稳定性计算结果偏低，特别是对罕遇地震动工况和罕遇地震动工况，但静抗剪强度参数比动抗剪强度大又使计算结果偏高。

4)利用数值分析法计算地震动力作用，加载方式和材料参数与实际情况接近，计算结果相对可靠。

5)由于所选堤坝剖面在扬州段属较好情况，综合分析得到即使在基本地震动工况，强度折减系数只有0.7，稳定性状况较差，在堤坝临湖区域易产生严重地震灾害，应引起有关部门的高度重视。

参考文献:

[1]张大伟，曾红鹰，段祥宝，等.危险水力条件对堤坝稳定性影响的模拟[J].水运工程, 2010，(09):40-45.

[2]葛建.堤坝渗透变形及稳定性分析[J].水科学与工程技术,2005，(06):48-50.

[3]张西文,唐小微,渦岡良介.液化场地堤坝地震响应的自适应步长法数值模拟[J].水利学报,2014，(09):102-109.

[4]田贵川,何江达,肖明砾，等.基于动力有限元法的土石坝地震响应及稳定性分析[J].四川水力发电, 2010，(01): 106-111.

[5]陈建宏，张涛，曾向农，等.尾矿坝边坡稳定性仿真建模与安全分析[J].中南大学学报(自然科学版),2008，(04):5-10.

[6]李书兵，苏骏，毕辉.岩质边坡在地震荷载作用下的动力响应分析[J].地下空间与工程学报，2012，01:212-216.

[7]Huang C Z, Cao Y H, Sun W H. Generalized Limit Equilibrium Method for Slope Stability Analysis[J].Applied Mechanics & Materials, 2012, 170-173(3):557-568.

[8]吕擎峰，殷宗泽，王叔华，等.拟静力法边坡稳定分析的改进[J].岩土力学，2005，S1:35-38.

[9]言志信，高乐，彭宁波，等.顺层岩质边坡地震动力响应研究[J].岩土力学，2012，S2:85-90.