削弱齿槽转矩的定子结构设计*
2018-04-20张登明曾凡铨
张登明,周 阳,曾凡铨
(1.上海航天控制技术研究所·上海·201109;2.上海伺服系统工程技术研究中心·上海·201109)
0 引 言
永磁电机由永磁体励磁,无需励磁绕组,因此其电机的结构尺寸大大减小,同时具有功率密度高、调速范围宽、高效节能、易于控制等优点,在新能源汽车、空调、机器人等领域获得了广泛应用。
随着电机向超高速、低噪音方向发展,降低齿槽转矩变得尤为重要。针对齿槽转矩问题,国内外专家学者给出了不少降低齿槽转矩的方法,这包括:不等厚磁钢、磁极偏移、转子斜极、定子斜槽、定子齿开槽等方法[1-11]。本文给出了一种削弱齿槽转矩的新方法,即:将定子齿设计成无齿靴状,并在齿牙处开设燕尾槽,采用拼接式结构去除槽开口。
1 齿槽转矩产生的原理
齿槽转矩产生的机理为:在绕组不通电的情况下,永磁体和定子铁心之间发生相对转动,引发主磁路磁导产生变化,磁场能量分布随即发生了改变,进而产生机械转矩,该转矩是由永磁体与电枢齿之间的相互作用力的切向分量引起的。齿槽转矩在一定范围内不同转角下的大小不等,且存在周期性波动。当用手慢慢转动转子时,会发现若干个定位点,在自然状态下转子即定位于这些点,因此齿槽转矩又被称为定位转矩、顿转转矩。
将齿槽之间的相互作用力分解为径向力Fd和切向力Ft,由图1可知,只有切向力Ft对齿槽转矩有所贡献[12]。切向力在各转角处大小不等,沿圆周出现周期性波动变化,且切向力合力矩不为零,此合力矩即为齿槽转矩,如图1所示。
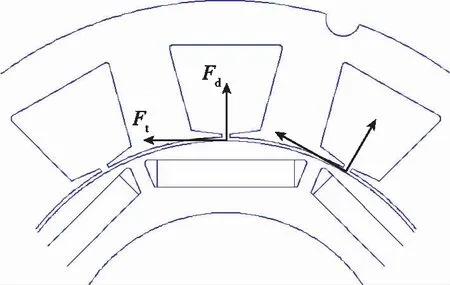
图1 齿槽转矩受力分析Fig.1 Force analysis of cogging torque
齿槽转矩可被定义为电机不通电时磁共能w相对于位置角α的导数,即:
(1)
假设电枢铁心的磁导率为无穷大,则电机内的存储能量可近似表示为:
(2)
式中,Wgap为电机气隙内磁场能量;WPM为永磁体内磁场能量;μ0为真空磁导率;B为磁感应强度;v为体积。
当转子相对位置发生变化时,永磁体内磁场能量可被认为不发生变化。齿槽转矩是因气隙磁场能量变化产生的,则气隙磁密沿定子表面的分布可以表示为:
(3)
式中,Br(θ)为永磁体剩磁;g(θ,α)为有效气隙长度;hM(θ)为永磁体充磁方向厚度。气隙内磁场能量可表示为:
(4)
式中,LFe为定子铁心轴向长度;R1为转子外径;R2为定子内径。

(5)
其中
(6)
(7)
将式(6)、式(7)带入式(5)中,得到:
(8)
式中,p为极对数;αp为永磁体极弧系数。

(9)
将式(9)代入到式(1)中,得到:
(10)

2 削弱齿槽转矩的定子结构设计
由齿槽转矩的计算公式可知,齿槽转矩的大小受槽数、极数、极弧系数、气隙厚度等因素的影响,因此可以从槽极配合、气隙厚度、定转子结构尺寸等方向着手优化齿槽转矩。
国内外专家学者研究出了不少减少齿槽转矩的方法,方法具体归纳如图2所示。本文中削弱齿槽转矩的方法不同于传统方式,而是将定子齿靴去除,并在齿牙处开设燕尾槽,采用拼接式结构去除槽开口,具体结构形式如图3所示。由于齿槽转矩是由定子齿槽磁导率发生变化而产生的附加谐波转矩引起的,因此此结构形式将槽口封闭,可以大大降低齿槽磁导率的变化,进而有效降低齿槽转矩。
图3(a)中的定子冲片齿牙处开有燕尾槽,图3(b)的拼接结构由硅钢片叠压并进行激光焊接而成。将拼接结构与定子通过形状配合、紧密连接在一起,构成定子组件,如图3(c)所示。拼接结构与定子紧密结合,使得连接处的缝隙非常小,此处的磁导率和硅钢片磁导率几乎相同,因此不会影响硅钢片的导磁性能。采用拼接式结构具有以下两点优势:
(1)由于没有齿靴的妨碍,定子在绕线时,可以很方便地采用手工绕线或机器绕线方式。
(2)嵌线之后的定子与拼接件紧密结合。由于没有槽口,定子齿槽处的磁导率变化很小,能够有效地削弱齿槽转矩,降低转矩波动。

图2 电机齿槽转矩的优化方法Fig.2 Optimization method for cogging torque of motor
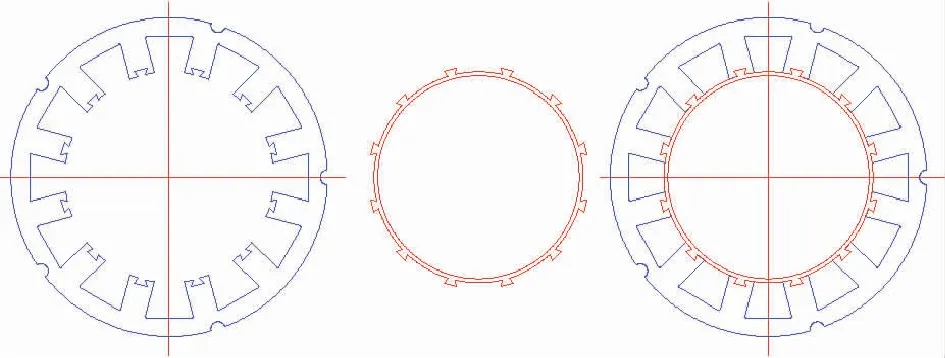
图3 定子拼接结构Fig.3 Stator splicing structure
3 电机齿槽转矩仿真分析与对比
在此,利用场路耦合的方法[13],借助有限元分析软件研究在定子齿部不设计齿靴及采用拼接结构对齿槽转矩的影响。选取额定功率4kW、额定转矩12.8Nm、额定转速3000r/min、8极12槽嵌入式永磁同步电机为研究对象,电机的主要结构参数如表1所示,电机的机械特性曲线如图4(x轴表示电角度,y1轴表示输出功率,y2轴表示输入电流,y3表示效率)所示,显示了输出功率、输入电流和效率随转矩角的变化。由图4可知,电机在额定负载时的转矩角为44.8645°,输出功率为4079.9988W,输入电流为16.0545A,效率为94.15%。
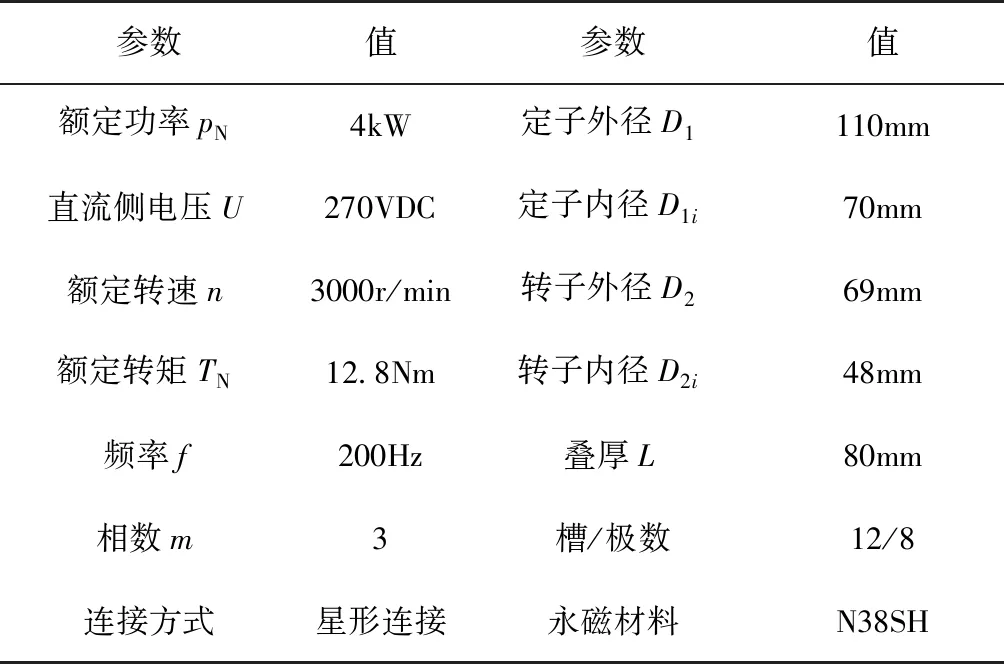
表1 电机结构参数Tab.1 Structural parameters of motor

图4 机械特性曲线Fig.4 Mechanical characteristic
将传统嵌入式永磁同步电机在静态场下进行分析,得出电机空载磁力线分布如图5(a)所示;将该电机定子设计成拼接结构,在其他结构参数保持不变的前提下,进行静态场分析,得出电机空载磁力线分布如图5(b)所示。通过对比可知,拼接式结构的拼接缝隙并不影响定子铁芯的导磁性能,反而可增大铁心的导磁性能及磁力线密度。

(a)传统结构中的磁力线分布(a)Distribution of magnetic line in traditional structure

(b)拼接式结构中的磁力线分布(b)Magnetic line distribution in spliced structure图5 空载状态下的磁力线Fig.5 Magnetic line in empty state
对传统嵌入式永磁同步电机的槽开口尺寸进行参数化扫描(扫描范围为0.1mm~1.5mm),由图6(x轴表示槽口宽度,y轴表示齿槽转矩)可知,定子槽口宽度越大,齿槽转矩越大。槽口宽度为0.1mm时,齿槽转矩最小,约为10mN·m;但在实际生产过程中,槽口宽度不可能低至0.1mm,否则无法嵌线。拼接式定子结构的槽口宽度为0,其齿槽转矩波动如图7(x轴表示电角度,y轴表示齿槽转矩)所示。由图7可知,拼接式结构齿槽转矩的最大值为7.88mN·m,比槽口宽度为0.1mm的齿槽转矩更小。通过图7中的传统嵌入式永磁同步电机齿槽转矩与拼接式永磁同步电机齿槽转矩的对比,可知拼接式定子结构较传统定子结构更能有效降低齿槽转矩。
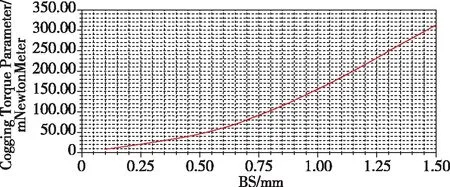
图6 槽口宽度与齿槽转矩关系曲线Fig.6 The relationship between slot width and cogging torque
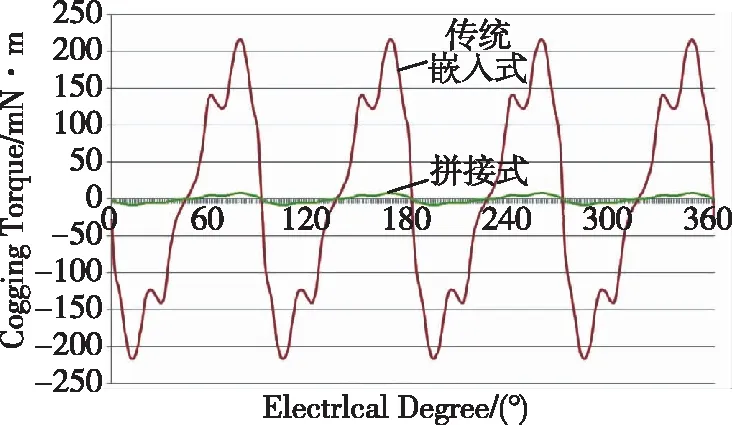
图7 传统定子结构与拼接式定子结构的齿槽转矩对比Fig.7 Comparison of cogging torque between traditional and spliced stator structure
4 结 论
本文在研究齿槽转矩的产生机理和解析公式的基础上,采用定子拼接式结构来削弱永磁电机的齿槽转矩。详细阐述了拼接式定子结构的模型,以1台永磁同步电机的样机参数为参考,将样机定子改为拼接式结构并进行了仿真分析。通过对比,证明了拼接式定子结构可大大降低定子齿槽转矩。研究得出以下结论:
(1)定子拼接式结构的拼接缝隙很小,磁阻变化很小,不影响硅钢片的导磁性能;
(2)拼接式结构的槽开口为零,使得更多的磁力线能够跨过气隙进入定子齿部,能增大磁力线密度;
(3)拼接式定子能大大降低齿槽转矩,转矩比0.1mm槽口的齿槽转矩更小;
(4)拼接式定子结构在未拼接前,定子槽敞开,方便手工绕线和机器绕线,可提高槽满率;
(5)在同一永磁电机模型中,槽开口越大,齿槽转矩就越大。
