地铁站可达性和便利性对通勤选择的影响研究
——以上海市中心城区地铁站为例
2018-04-19刘晓璨
刘晓璨
(上海交通大学 安泰经济与管理学院,上海 200030)
本文以上海市中心城区地铁站点为研究对象,根据居民公交卡刷卡记录,结合地铁站点的自身特征,探讨地铁站点的可达性与便利性对通勤出行站点选择的效应,建立地铁通勤出行站点选择模型,为公共交通部门在轨道交通建设中合理规划轨道站点布局提出参考建议。
1 模型建立
1.1 数据描述
本文研究数据主要来源于上海市居民的一卡通交通卡刷卡记录,以及轨道交通官网公开信息和地图API开放数据。收集到2015年4月13日至4月17日(连续一周工作日)的交通卡刷卡记录,数据格式为ID、刷卡日期、刷卡时间、线路、交通方式、价格、优惠。居民通勤出行时间往往集中于上下班早晚高峰,为了筛选出通勤人员的记录,按照每小时间隔,将一天划分为24个时间段(0代表0:00-1:00,…),统计出连续一周工作日中每个时间段内的刷卡记录数,分布情况如图1所示。
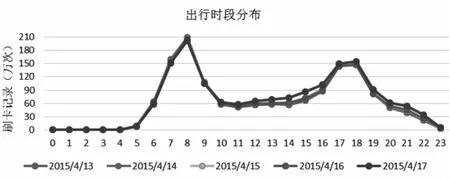
图1 每日出行数时段分布
由出行记录数在各时段的分布可知,公共交通出行分布规律稳定,出行有两段明显的高峰期:时段7(7:00-8:00)和8(8:00-9:00),17(17:00-18:00)和18(18:00-19:00)。因此,将此时间段作为本文研究对象的通勤时间。对于通勤出行研究即上班出行时对地铁站点的选择情况,则只需要考虑早高峰时期的地铁进站点。观察连续五个工作日的交通情况,选出乘坐地铁的工作通勤出行记录(符合通勤的条件:连续5天每天上下午高峰期均有乘地铁记录),最终筛选出216825位通勤出行乘客。
出行者可以在地铁站点中做出选择的前提是,居住地周围需要有多于1个地铁站构成备选集,这就要求被研究的地铁站点在地理位置上分布相对密集。综合考虑地铁站线路、数量、客流量、区域面积等因素,本文将研究范围定为上海市中心城市范围内,以分布在中心城区地带的50个地铁站为研究对象,对居民通勤上班时选择地铁站点的行为进行研究,筛选出符合条件的138320条观测记录。
1.2 基本定义和假设
本文从地铁站点的可达性和便利性两大方面研究通勤出行对地铁站点的选择行为,可达性定义为地铁站点对于出行者的可接近性,包括地铁站点与出行者之间的距离、地铁站点附近的公交线路数。便利性定义为地铁站点的特征对于出行者使用体验的影响作用,用地铁站的拥挤程度、出入口数、地铁站所经列车的发车频次来衡量。为了避免地铁站点所处线路的不同带来的影响,将地铁站所处线路设为控制变量,重点考察地铁站点的可达性及便利性中的拥挤程度和出入口数对站点选择行为的作用。根据研究需求,本文提出以下假设:
H1:出行者与地铁站间的距离对通勤出行的选择行为具有负效应。
出行者在面对大于1个的可选地铁站时,往往会倾向于选择距离自己近、步行距离短的站点,距离的增加会减少用户的选择意向。
H2:地铁站点周围公交线路的增加会减少用户对地铁的选择。
地铁站周围的公交车与地铁站是潜在的竞争关系,虽然地铁站具有时速快的优点,但公交车也有进出方便等优势。因此,作为可互相替代的交通工具,地铁站周围的公交具有客流分流作用。公交车数量越多,越有可能减少出行者对地铁站的选择。
H3:地铁站拥挤程度的增加会降低出行者的选择意向。
由于不同地铁站所处位置不同、所到地区不同而拥有不同的客流量,热门地铁站往往非常拥挤,途径商业聚集区的地铁站在早晚高峰期客流非常密集。人们在通勤出行时由于赶时间等因素,会对拥挤程度有敏感性。地铁站越拥挤,人们对此的体验越差,从而倾向于避开拥挤度高的地铁站。
H4:地铁站的出入口数量对出行者选择有正效用。
地铁站的出入口数一定程度上反映了地铁站的空间大小,出入口数对客流量疏散也有重要作用。出入口数越多,越能增强人们的乘车便利性,从而增加选择意向。
1.3 基于BLP的选择模型
国内外对于交通方面的研究大多建立在问卷调查基础上,获取个人的社会经济属性特征,结合实际交通数据进行分析。本文所进行的需求分析建立在集计层面数据的基础上,即不通过问卷调查获取个体特征,利用随机系数离散选择模型的加总方法消除个体层面数据的影响,也可称为BLP(Berry-Lavinsohn-Pakes)模型。BLP通过引入工具变量来解决解释变量的内生性问题,同时考虑竞争产品的特征,允许商品和消费者具有无法观测的特征,比常用的Logit模型或Nested Logit模型有灵活的计量特征,应用BLP方法对差异化的产品需求进行研究已被广泛应用于理论及实践研究中。本文参考BLP理论模型,将不同的地铁站点看作空间分布差异化的商品,将通勤出行者看作做出选择决策的消费者,利用地铁站点刷卡的集计数据,并考虑出行者距离的异质特征,建立通勤出行者对于地铁站点的随机系数离散选择模型。
假设有t=1,2,…,T个可观测的市场,含有i=1,2,…,It个消费者,面对j=1,2,…,J种可选商品。每个市场中商品的总需求和商品特征是可知的,假设市场之间互相独立,市场可以代表地区性、时间序列等。令表示消费者i在t阶段使用商品j所获得的效用,则

xjt——商品j在t时可观测到的特征,K×1列向量。本文模型中相应的站点可观测特征为地铁站点可达性中的与出行者之间的距离、周围公交线路数,以及便利性中的地铁站点拥挤度、出入口数量、高峰期列车发车频次特征。
βi——K1维的系数向量,商品特征的边际效用,根据消费者个人特征展现个人对商品特征的不同偏好,βi=(βi1,…,βiK)T。
ξjt——在t时未观测到的商品特征对所有消费者的共同效用。本文模型中可能存在未观测到的站点特征对通勤出行选择有影响,如存在用户主观感受到的、无法被研究获知衡量的站点可达性特征或便利性特征。
εijt-均值为0的随机误差项,假设服从独立同分布(i.i.d)。
考虑在给定区域内空间分布的出行者是倾向于效用最大化的,出行者可在居住地周围的地铁站点中做出地铁通勤选择,或者选择公交车等其他交通方式。则出行者i在通勤早高峰期(固定t)选择地铁站j∈{1,…,J}的间接效用为

Li——出行者的起始位置,体现了个体的异质性。
d(Li,Lj)——出行者的位置与地铁站的位置特征决定的出行者i与地铁站j之间的距离。
h(·)——捕捉出发地与地铁站之间距离效应的参数函数,体现了交通成本特点。
nbusj——地铁站j周围的公交车线路数,利用地图API开放接口抓取地铁站点周围1800米范围内经过的公交车线路数。
crowdj——地铁站j在早高峰期的拥挤程度,由地铁站历史客流数据,统计同时段进站的客流量来表示。
entrj——地铁站j的入口数量,由地铁官网信息统计所得。
freqj——地铁站j的发车频率,由官网公布的列车高峰期发车间隔数据,计算出高峰期间站点所经过的列车次数来表示。
γnl(j)——地铁站j所在线路的固定影响,为虚拟变量。
ξj——未观察到的地铁站j的特征,假设可被出行者观察到且对所有出行者效用一致。地铁站点隐含研究无法观测到的特征对出行选择产生影响,如站点与周围其他地铁站距离关系等影响站点可达性的因素,站点舒适度、整洁性等影响乘客感知便利性的因素,因此,本文将假设中可能遗漏的隐含在地铁站可达性和便利性特征中的因素放在ξj中,并在后文提出针对未观测到的遗漏变量对于模型内生性影响的工具变量方法。
模型包含外部商品的假设,即除地铁外,出行者选择其他交通方式的效用为

消费者个人特征没有直接出现在效用模型中,而是体现在对商品特征的边际效用的决定作用上。个体特征由可观测的人口统计因素Di(d×1列向量)和不可观测的其他特征vi(K×1列向量)组成,则随机系数可表示成对所有消费者一致的均值部分和体现个人差异的部分:

Π——K×d可观测系数矩阵,衡量人口统计变量对于偏好的重要程度。
Σ——K×K对角矩阵,捕捉未观测到的消费者变量对偏好的影响,Σ=diag(σ1,…,σK)。
Di和vi的分布分别记为P*D(D)和P*v(v),假设P*v(v)服从多元正态分布。定义包含线性参数的向量θ1=β,包含非线性参数的向量θ2=(Π,Σ),则向量θ=(θ1,θ2)包含了模型中的所有结构参数。因此,效用函数可分解为对所有消费者都一致的部分δjt(xjt,ξjt;θ1)与体现消费者异质性特征的部分μijt(xjt,Di,vi;θ2)之和:口统计特征Di。假设个人的其他特征对于选择行为没有显著影响,因此,这里可不考虑vi。因此,令
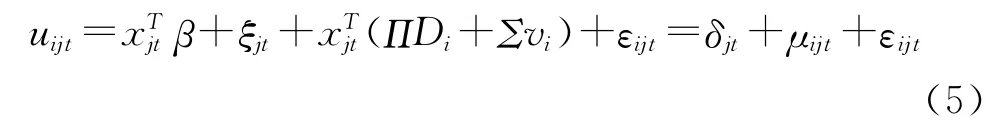
本文模型中体现个体特征的部分为出行者与地铁站之间的距离,由出行者的位置与地铁站的位置特征决定。个人的出行位置无法准确得到,本文采用将个人层面数据加总的方法。假设人口均匀分布,将研究区域划分为边长为D米的方格,以每个方格中心点代表出行用户的质点集合,用地图上的经纬度来计算出行用户与站点间的理论距离。为了在地图上方便划分方格,以及考虑出行者通常的步行范围,取D为经纬度上的0.01度,约为1km。由此,得到的距离特征可对应为BLP理论模型中的人效用函数中对所有出行者都一致的无差异效用为

当居住地附近有可以互为替代的不同地铁站时,出行者会综合考虑比较地铁站可达性与便利性特征,从中选择能使自己获得最大效用的地铁站。选择某一地铁站的概率遵循Logit模型。令Si为出行者i可选的地铁站集合,则出行者i在高峰期选择地铁站的概率为ξ.表示未观测到的特征向量,θ代表所有参数值(β0,β1,…,βd及固定效用γ),又表示为

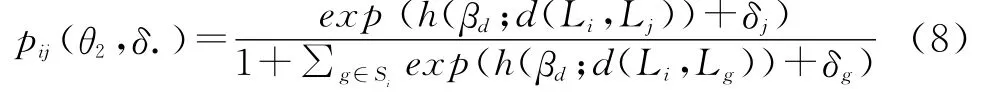
商品j在t时的市场份额为所有消费者选择集合:

sjt无法直接用积分计算出真实值,但可以用随机样本选择概率加总近似计算。本文对应的地铁站市场份额为某地铁站被选作通勤出行的次数在所有通勤选择中的占比,则可近似表示为
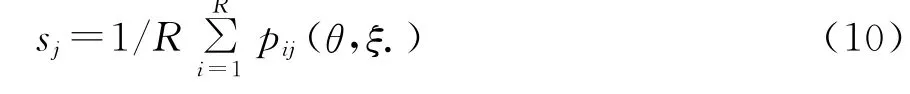
BLP方法通过构造GMM(广义矩估计)估计量对模型参数进行一致估计,本质是对于给定的未知参数值,计算隐含的误差项并与工具变量交互,从而形成GMM 目标函数E[Zjtξjt(θ*)]=0,在约束条件s(x,δ;θ)=S下搜索所有可能的参数值来寻找使目标函数最小的值,s(x,δ;θ)为市场份额的预测值,S为实际观察值。
2 模型估计与分析
2.1 内生性与工具变量
参考Kabra(2016)对公共自行车系统的研究,本文模型中的不同地铁站点是差异化的产品,出行者到地铁站的距离是差异化的产品特征,不可观测到的异质特征是出行者的起始位置。当存在不可观测的产品特征(遗漏变量),或数据子集之间存在不一致时(测量误差),容易出现内生性偏差,即解释变量与未知的误差项之间具有相关性,如前文提到的未观测到的地铁站点可达性或便利性特征对于出行选择的影响。BLP方法使用自身和竞争产品特征的子集来提供有效工具变量。在地铁站点的需求模型中,地铁站的拥挤程度是内生性决定属性,对此设置相应的工具变量来使模型得到有效无偏估计,工具变量可概括为目标地铁站附近的竞争特征。
假设出行者在做出站点选择决策之前,根据已有经验观察感知到备选集合站点在出行时段的拥挤程度,并将此作为决策考虑的一个因素。如果目标地铁站的拥挤程度比可为替代的邻站拥挤程度高,则出行者对目标车站的需求可能会降低;而目标地铁站被选次数减少,则其拥挤程度相应降低。因此,地铁站的拥挤程度与需求之间有互相影响关系。合适的工具变量需要与内生解释变量或需求项相关,一种影响需求的因素来自会造成需求转移的竞争地铁站,相应选取工具变量为地铁站j到最近地铁站的距离、到最近5个地铁站的平均距离以及周围2千米内其他地铁站的数量。这组工具变量体现了地铁站的被替代可能性,周围的地铁站会造成潜在的客流分流,某地铁站与其最邻近的地铁站之间的距离越远,或者周围地铁站数量越少,则其他同条件下,它的拥挤程度可能会更高。这组工具变量也隐含着地铁站点的空间分布的密集程度,间接体现出地铁站点对用户的可达性特征,对应了模型中未观测到的地铁站点可达性特征中的因素对选择行为的影响。
拥挤程度的直观含义为在某时刻地铁站内聚集的候车乘客数,或地铁车厢里的乘客数,但此项精确数据难以获取(涉及上下车厢的乘客数量变化)。与出行者有直接影响关系的是同时段进入地铁站的客流量,因此,本文采用地铁站的乘客进站量来衡量地铁站的拥挤程度。经描述统计分析可知,地铁站每天的客流量情况比较平稳,因此,可任意选取前一周内任意两天工作日的地铁站早高峰期乘车记录,用平均进站客流量来表示地铁站的拥挤程度crowdj=早高峰期j地铁站进站人数。
综上,本文考虑的工具变量分别为目标地铁站与其最近地铁站的距离、到最近5个地铁站的平均距离、周围2千米内的地铁站数量。内生性与工具变量的结构关系为:

表1 内生性变量与工具变量 (来源:地图API)
2.2 工具变量的检验2SLS
工具变量用于估计时,通过二阶段最小二乘法2SLS(Two Stage of Least Square)来进行参数估计,2SLS的第一阶段回归可用来检验工具变量与内生解释变量的关系。通过第一阶段工具变量回归(表2),即内生解释变量对工具变量的回归,可看出内生性解释变量拥挤度可被表示为工具变量的线性组合。回归结果在5%和10%的水平上显著,说明工具变量与对应的内生性解释变量高度相关,有助于评价工具变量的有效性。

表2 2SLS第一阶段工具变量回归
2.3 GMM估计算法
根据BLP方法所采用的GMM(广义矩估计)算法,构造GMM矩条件,使得未观察的误差项ξj在参数真值θ*时与工具变量Zj无关,形成GMM估计量目标函数与约束条件:
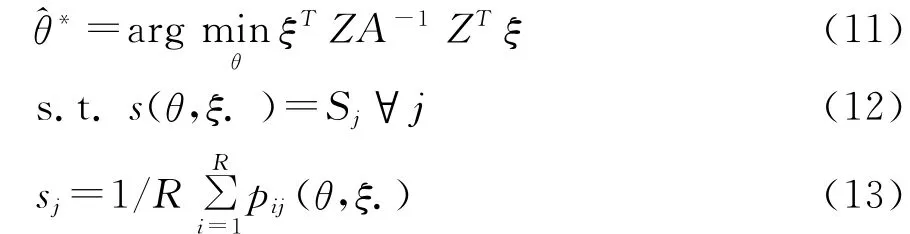
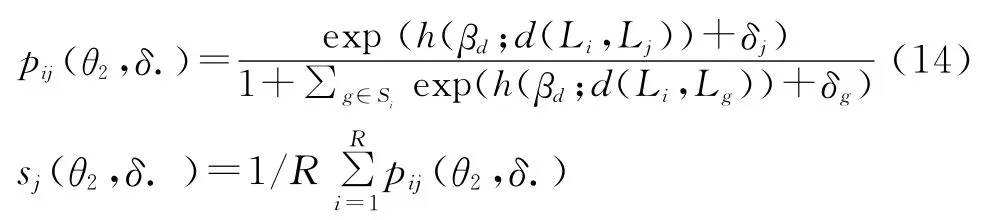
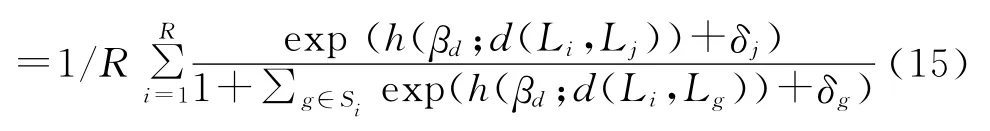

求解等式s(δ.;θ2)=S,转换出δ后,误差项为则市场份额实际值 S进入了等式。这也体现出区分θ1,θ2的原因:θ1以线性型进入此项和GMM目标函数,θ2非线性进入,从而减轻非线性最优问题的计算复杂度。
2.4 估计过程
模型估计过程对参数值θ2,δ进行搜索,先对θ2,δ进行任意赋值,通过内外两层循环迭代求出最优的θ2,δ值。内循环为固定住θ2后迭代出最优的δ值,外循环为搜索θ2使得目标函数最小化。BLP使用压缩映射方法来进行转换求解,估计过程流程图如图2所示。
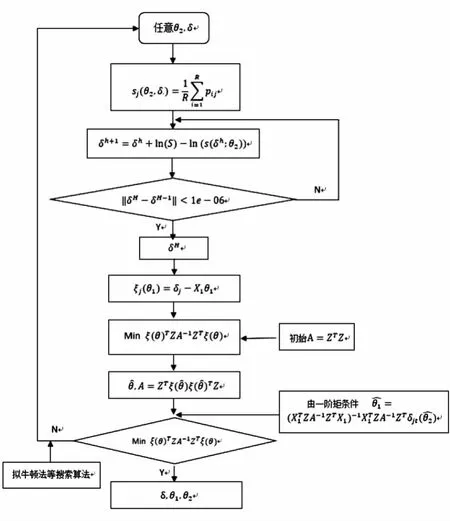
图2 模型求解过程流程
2.5 估计结果
本文用R分析工具对模型参数进行估计,借鉴其他的非线性规划程序包进行改编,并利用优化的搜索方式,使得原本嵌套迭代的模型计算速度大大提高。迭代循环设置的停止临界值为1e-06。在目标函数值为3.285e-07时结果收敛,各参数及线路虚拟变量的估计结果如表3所示,未观测到的站点特征影响如表4所示。

表3 模型主要参数估计结果

表4 各站点特征的估计值
根据参数估计的结果,可以初步得出以下分析结论:
(1)出行者与地铁站之间的步行距离对选择行为有显著负效应,与本文的假设相符合,人们总是倾向于选择距离自己更近的地铁站,减少步行距离。地铁站点距离出行者过近则会造成分布密集的问题,对于工程建设及资源都会带来挑战,且过多停靠站点也会带来运行效率降低的问题。因此,地铁站点选址要找到与用户距离合适的分布点,以发挥站点的最大效用。
(2)地铁站附近经过的公交车线路数量对通勤出行者的选择行为有显著负效应,且在所有因素中有影响效应最大。这说明地铁站与公交车的接驳性对地铁站的客流具有分流作用,即地铁站周围的公交车线路越多,出行者越可能去选择公交车来代替地铁。因此,若要增加公交车对地铁的客流分流,则对于地铁站点周围公交线路的接驳数量可适当增加;若要增加地铁对公交客流的分流,可减少周围的公交线路,但在两者互相分流中要取得平衡。
(3)地铁站的拥挤程度对通勤出行者的选择有显著负效应,与本文的假设相符合,出行者更倾向于选择客流量少、拥挤程度低的地铁站,以增加乘车的舒适感受。在现有客流量的基础上,地铁站点可适当增加对客流的疏导,以减轻乘客对空间拥挤度的直观感受。
(4)地铁站的出入口数对通勤出行者的选择有显著正效应。地铁站的出入口数一定程度上反映了地铁站的规模,地铁站面积或空间越大,所含出入口可能越多,对于客流量的疏散作用也越强。因此,乘客会倾向于选择出入口较多的地铁站。但此项影响系数较小,因此,在建设工程资源约束下,对地铁站出入口的建设可进行适当增减。
(5)地铁站在高峰期的发车频次对通勤出行者的选择行为有负效应。这一结果与通常情况下地铁发车频率越高,越能吸引出行者的选择这一认知有出入。本文认为,造成这一结果的原因是由于数据收集出现偏差。本文所考虑的地铁发车频次是根据轨道交通官网上公布的地铁在高峰时期的发车间隔时间计算所得,有些地铁线路的发车间隔公布的是一个范围,而不是精确到一个数值,说明地铁列车在实际运行中的发车间隔会有不确定性。因此,这也会造成收集的数据有偏差。
作为控制变量的地铁线路虚拟变量除了1号线,其他线路均有显著效应,说明地铁站所处线路对于出行选择有影响。1号线对于通勤出行选择没有显著影响的原因可能是,经过中心城区的地铁1号线上的地铁站大多处于客流聚集的重要交通地带,且其可到达的目的地含有工作聚集地,对出行者来说具有不可替代性,因此,出行者对其站点没有明显偏好。6,7,9,11号线对于通勤选择有负效应,因为线路上大多数站点客流量大,且含有典型的拥挤站点如徐家汇、静安寺、江苏路等,会影响出行者对便利性的感受。
不同地铁站未观测到的可达性或便利性特征对出行选择的影响程度不同,有些站点可能因为其站内更好的干净整洁度、提供更多便民服务等特征,对出行选择有正效应。有些站点可能因为站内设施建设不够便民等影响用户的乘车体验,从而降低了用户的选择意愿。
3 结论与展望
本文提供了地铁站点的可达性与便利性对通勤出行选择效应的实证研究,利用集计层面的数据考察异质性个体特征。研究发现,地铁站点的可达性与便利性对通勤选择行为有显著影响。其中,可达性中的地铁站与出行者之间的距离、地铁站周围的公交线路数对选择有负效应,因此,在规划地铁站点分布时,除了要在居民集聚地增加站点以减少居民步行距离外,还要考虑公交车与地铁站的互相分流作用,合理规划地铁周围的公交接驳,以达到平衡载流量。地铁站的便利性特征对出行选择也有影响,适当增加地铁站的出入口数可更好地引导客流,为出行提供便利。地铁站的拥挤度对于通勤出行选择来说有负影响,若想增加通勤时的选择行为,要疏散掉较多的客流,且二者之间有互相影响关系。因此,在保持客流现状的基础上,可增加客流疏导服务,如增加进出口通道等,以减少乘客对拥挤密度的感受。在未来规划新地铁站点时,可适当增加站内空间及出入口数。
由于研究数据所限,本研究是相关领域的初探,今后还可从更多方面进行挖掘。若能获取到细分、准确的区域人口统计信息,则选择模型中反映地铁站点间相对关系的市场份额可用选择人数来代替,从而考虑到地区的人口分布异质性特征。若能收集到更全面的数据,研究还可从中心城市扩展到更多地区,并考虑站点所属地区的居住性、商业性等特征,从而进行更多角度的比较分析,为轨道交通站点建设规划提出更多角度的参考建议。
参考文献:
[1] MURRAY A T,WU X l.Accessibility tradeoffs in public transit planning[J].Journal of Geographical Systems,2003,5(1):93-107.
[2] OLSZEWSKI P,WIBOWO S S.Using equivalent walking distance to assess pedestrian accessibility to transit stations in singapore[J].Transportation Research Record:Journal of the Transportation Research Board,2005,(1927):38-45.
[3] MAMUN S A,LOWMES N E.Access and connectivity trade-offs in transit stop location[J].Transportation Research Record:Journal of the Transportation Research Board,2014,(2466):1-11.
[4] 程立勤.轨道交通与常规公交协调发展研究[J].物流工程与管理,2012,34(212):73-74.
[5] 周昭明,查伟雄.基于常规公交的轨道交通站点吸引范围研究[J].交通科技与经济,2014,16(6):83-86.
[6] CROCKETT J,HOUNSELL N.Role of the travel factor convenience in rail travel and a framework for its assessment[J].Transport Reviews,2005,25(5):535-555.
[7] LITMAN T.Valuing transit service quality improvements[J].Journal of Public Transportation,2008,11(2):43-63.
[8] EBOLI L,MAZZULLA G.Relationships between rail passengers’satisfaction and service quality:a framework for identifying key service factors[J].Public Transport,2015,(7):185-201.
[9] EBOLI L,MAZZULLA G.A Methodology for evaluating transit service quality based on subjective and objective measures from the passenger’s point of view[J].Transport Policy,2011(18):172-181.
[10] BERRY S,LEVINSOHN J,PAKES A.Automobile prices in market equilibrium [J].Econometrica,1995,63(4):841-890.
