TBM滚刀布置方案对比分析与评价

崔 胤， 贺 飞， 齐志冲， 贺开伟

(中铁工程装备集团有限公司, 河南 郑州 450016)

0 引言

TBM是一种用于隧道全断面开挖的大型专用工程机械，被广泛应用于水电、铁路、地铁隧道工程施工[1]。刀盘作为TBM的关键部件，具有切削破碎岩石、传递破岩载荷、维持掌子面稳定和出渣排渣等作用。滚刀在刀盘上的安装布置设计是刀盘结构设计的重要内容，直接决定了滚刀的破岩效果和刀盘的力学性能，同时对刀盘后端主轴承的寿命、推进和驱动系统的选型设计也具有重要影响。

针对滚刀的布置设计，国内外已有研究主要集中在滚刀布置模式的优化方面。文献[2-5]利用遗传算法、蚁群算法和协同进化算法等数学方法对多随机式、米字型和随机式滚刀布置模式进行了优化，研究表明滚刀布置不仅影响刀盘的受力平衡，而且影响刀盘的强度和刚度，同时认为随机式滚刀布置模式可以设计出最多的布置方案，因而是最理想的布置模式；文献[6-8]提出一种微调滚刀极角的滚刀布置优化方法，采用灰关联分析算法进行了求解，结果表明该方法可以在不影响刀盘强度和刚度的前提下大幅提升刀盘的受力平衡效果；文献[9-10]采用遗传算法，对刀盘上的盘形滚刀布置进行优化，可以在一定程度上减小刀盘的不平衡力；文献[11]对多随机滚刀布置模式进行了数学分析，基于最小径向不平衡力和倾覆力矩的设计原则，对比分析了不同旋臂数目的多随机滚刀布置的刀盘力学性能；文献[12]基于相邻刀号的滚刀对称布置设计原则，编制了 TBM 刀盘布置设计与分析模拟软件。上述研究主要集中在滚刀布置对刀盘总体受力平衡的影响，而刀盘的受力平衡只是研究滚刀布置优劣的一个方面，滚刀的布置形式对刀盘局部受力的影响及滚刀的相对位置合理性均未曾涉及。

本文基于TBM刀盘的2种滚刀布置设计方案，对比研究其滚刀群径向不平衡力、倾覆力矩和质心偏移量，通过建立2种刀盘的有限元模型，对比计算了刀盘的变形和应力分布，提出滚刀相对位置的概念和滚刀分布密度这一评价滚刀相对位置的评价指标，将滚刀分布密度与刀盘变形进行了关联分析，揭示了滚刀分布密度变化和刀盘变形之间的一致性变化趋势，为通过滚刀分布密度指导滚刀布置设计提供了依据。

1 滚刀布置设计方案

刀盘开挖直径为7 930 mm，采用平面式刀盘结构，刀盘面板为箱型结构，前面板厚度为270 mm。

在刀盘设计过程中，提出2种滚刀布置方案，如图1所示。方案1基于米字型布置模式设计，方案2基于随机式布置模式并融合了自主设计理念。方案1包括8把17英寸(43.18 cm)中心刀、32把19英寸(48.26 cm)正滚刀和10把19英寸(48.26 cm)边滚刀； 方案2包括8把17英寸(43.18 cm)中心刀、36把19英寸(48.26 cm)正滚刀和12把19英寸(48.26 cm)边滚刀。通过对2种滚刀布置方案进行多方位对比分析，最终确定方案2为研究内容。2种滚刀布置方案的滚刀布置参数如表1和表2所示。

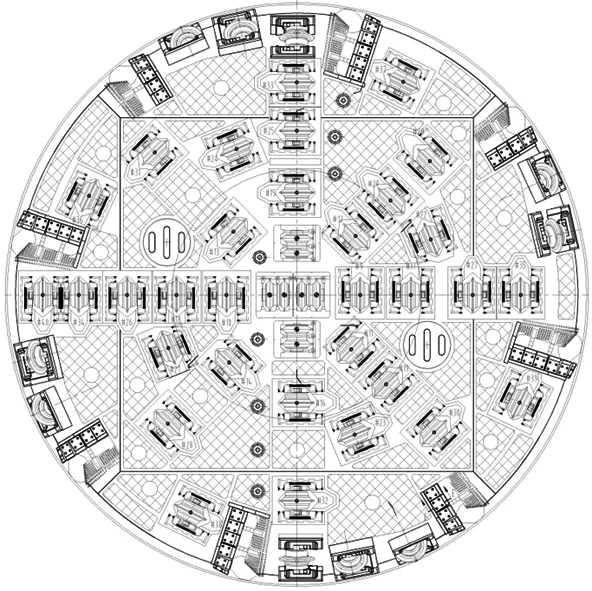
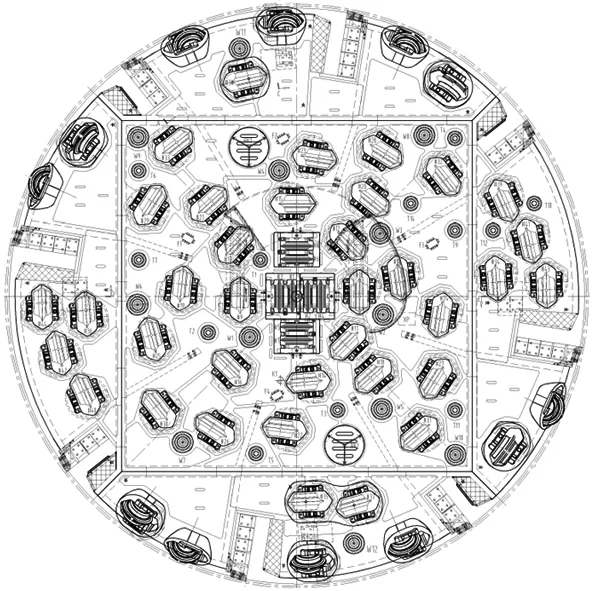
(a) 方案1： 米字型布置 (b) 方案2： 随机式布置

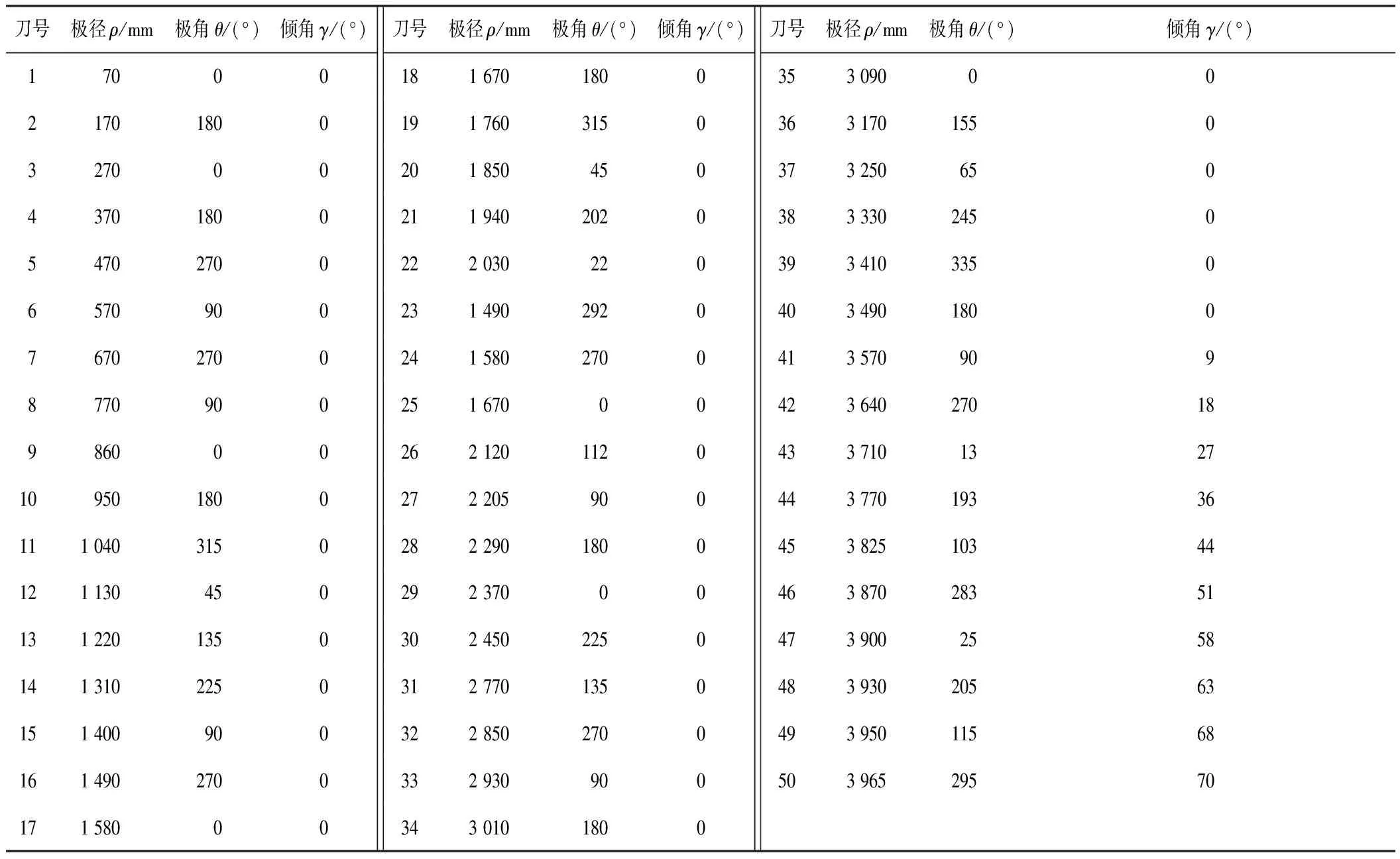
图1 滚刀布置设计方案示意图

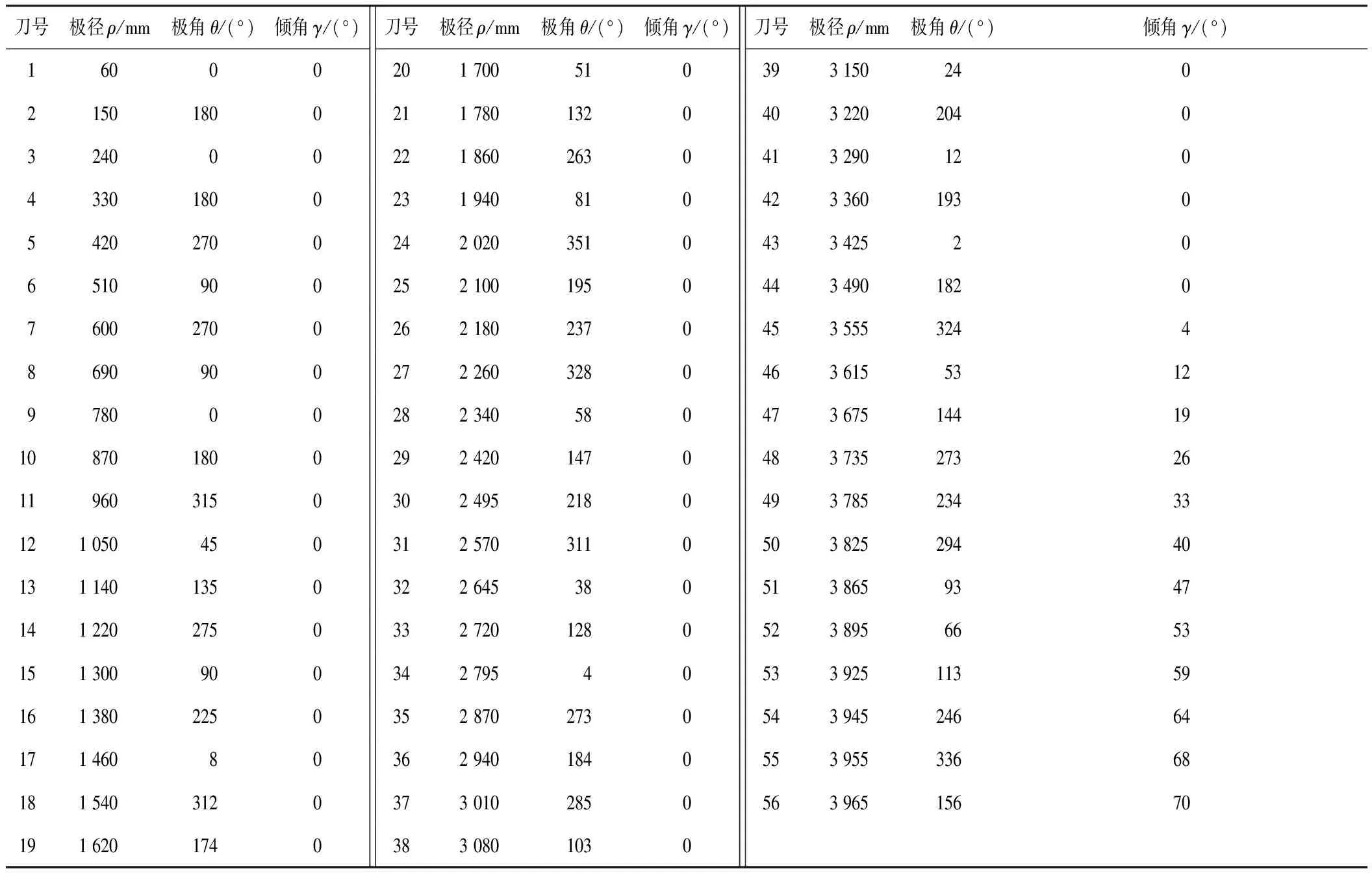
表2 滚刀布置方案2设计参数

2 滚刀布置对刀盘整体受力平衡的影响

2.1 刀盘受力平衡计算公式

为确保滚刀布置设计的可靠性，以19英寸(48.26 cm)滚刀的极限受力条件，即滚刀法向力FN为350 kN展开分析。根据CSM模型[13]，滚刀的切向力FR一般为法向力的1/10，因此取切向力FR为35 kN。对于边滚刀，取垂直于刀座的法向力FN1=FN·cosγ，侧向力FS=FN·sinγ，切向力FR=FN1/10。

刀盘受力平衡评价指标主要包括滚刀群径向不平衡力C1(kN)、倾覆力矩C2(kN·m)和质心偏斜量C3(mm)，其计算公式见式(1)—(7)[14]。

1)刀盘径向不平衡力

(1)

对于中心刀和正滚刀：

(2)

对于边滚刀：

(3)

式(1)—(3)中：Fx为径向不平衡力x轴向分力；Fy为径向不平衡力y轴向分力；Fb为边滚刀在极径方向的受力分量；FE为滚刀离心惯性力。

2)刀盘倾覆力矩

(4)

对于中心刀和正滚刀：

(5)

对于边滚刀：

(6)

式(4)—(6)中：Mx为倾覆力矩x轴向分量；My为倾覆力矩y轴向分量；Mg为滚刀的科氏惯性矩，Mg=mcω2ρr(其中，mc为滚刀质量，ω为刀盘转速，r为滚刀半径)。

3)滚刀群质心偏斜量

(7)

式中：C3为滚刀的位置沿刀盘轴线方向被投影到刀盘正面后，滚刀群质量的集中点(质心)与刀盘中心的偏斜距离； (x,y)为滚刀在xOy平面上的直角位置坐标。

2.2 刀盘受力平衡计算结果

计算得到刀盘的受力平衡性能评价指标C1、C2和C3，结果如表3所示。可以看到，虽然方案2的滚刀群径向不平衡力C1比方案1要大，但是其滚刀群倾覆力矩C2和质心偏斜量C3明显小于方案1，分别比方案1小约63%和69%，这说明滚刀布置方案2的刀盘受力平衡效果更好，对主轴承等关键部件造成的偏载影响更小。

表3刀盘受力平衡评价指标计算结果

Table 3 Calculation results of force balance evaluation index of cutterhead

方案C1/kNC2/(kN·m)C3/mm163．7693．954．72130．3255．816．9

3 滚刀分布密度对刀盘局部变形和应力的影响

3.1 滚刀分布密度

在滚刀布置设计过程中，除了需要考虑刀盘的整体受力平衡，还需要考虑刀盘的局部载荷均衡效果，为此本文提出滚刀分布密度评价指标C4，其定义为任意一把滚刀与其相距最近的N把滚刀的直线距离平均值的倒数，单位为mm-1。C4值越大，表明对应位置的滚刀分布越密，反之则越稀疏。刀盘上的滚刀分布越均匀，刀盘的局部受力也将更为均匀；反之，局部孤立的滚刀由于受临近滚刀的组合破岩影响小，破岩负载可能更大，容易加剧该区域的滚刀磨损消耗。

分别取N为2～10，计算2种滚刀布置方案中各刀位的滚刀分布密度C4，如图2所示。可以看到，滚刀分布密度C4随着刀号的增大而逐渐减小，这是由于在“一径一刀、等径布置”的滚刀布置基本原则下，刀盘中心区域的滚刀密度偏大，而刀盘外侧的滚刀密度相对较小且变化较为平缓。滚刀分布密度C4随着N值的增大而逐渐减小，当N>4时，曲线总体变得非常平缓，这是由于随着N值的增大，相邻最近滚刀间距的平均值增大，滚刀分布密度C4随之减小。对比不同N值的滚刀分布密度曲线，可以看到： 1)当N=2时，曲线波动剧烈且中心刀数值很大，这是由于仅考虑了与滚刀相邻最近的2把滚刀，数目偏小； 2)当N=3时，曲线较为平缓，但仍能明显反映局部波动的信息； 3)当N>4时，曲线趋于平缓，对于局部分布密度的形状信息反映不够明显。因此，取N=3时的滚刀分布密度作为评价各区域滚刀分布的基本评价指标。

把不同N值的滚刀分布密度结果在三维空间进行拟合，如图3所示，图中的X轴和Y轴表示刀盘面的坐标。可以看到： 1)曲面图呈明显的“山峰”形状，滚刀分布密度从刀盘中心区域向外周逐渐减小； 2)随着N值增大，中心“山峰”变得越来越平缓； 3)上述结果与图2所示的二维曲线结果相一致。

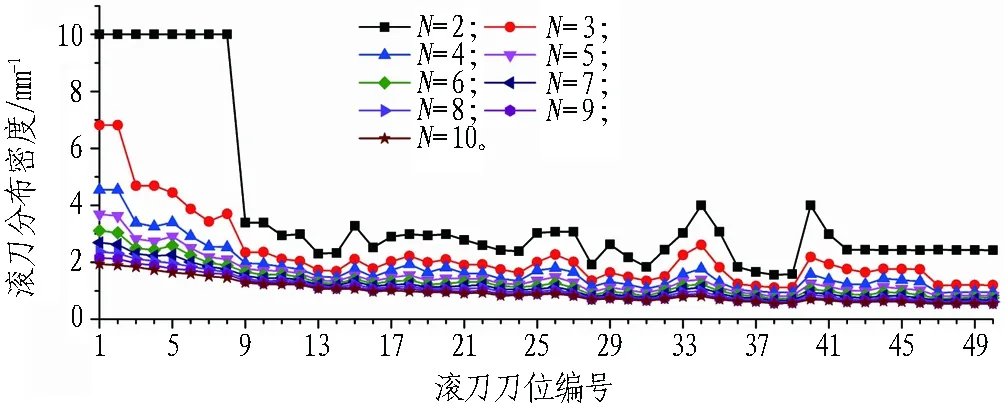
(a) 方案1

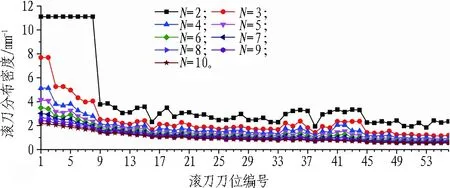
(b) 方案2

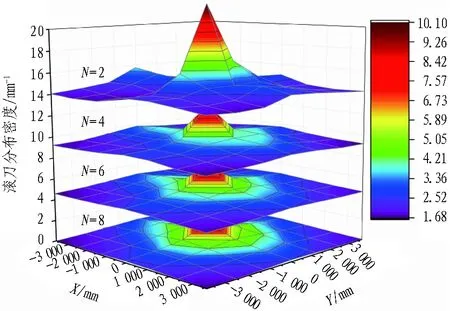
(a) 方案1

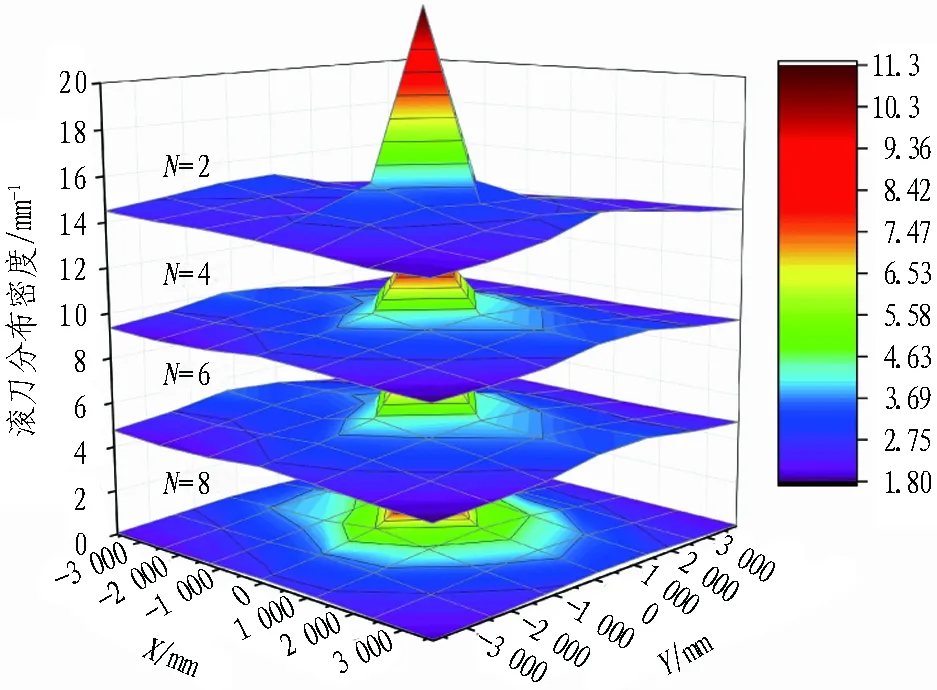
(b) 方案2

3.2 刀盘变形和应力有限元计算

滚刀的分布密度直接影响刀盘的受力变形和应力分布，滚刀分布密度越大，刀盘局部承受的载荷越大，相应的变形和应力也会增大，该区域更易发生损伤破坏。

根据滚刀布置参数，参照刀盘设计图纸，建立2种滚刀布置方案相应的刀盘有限元模型，如图4所示。

(a) 方案1

(b) 方案2

图4刀盘三维图

Fig. 4 3D models of cutterhead

2种刀盘的网格划分如图5所示。由于刀盘几何模型复杂，因而采用四面体网格对其划分，网格的平均尺寸为80 mm。方案1的网格数目为315 706，节点数目为513 485；方案2的网格数目为309 206，节点数目为515 952。刀盘材料取为Q345D，按弹性体考虑，密度为7 800 kg/m3，弹性模量E=210 GPa。

(a) 方案1

(b) 方案2

图5刀盘网格划分

Fig. 5 Meshing of cutterhead

在刀盘法兰后端面施加固定边界条件，用于约束刀盘体的轴向运动。将刀刃、刀体和刀轴等组成的滚刀装配体视为刚体，刀刃承受的载荷通过刀轴传递到与刀座接触的区域，因而可将载荷施加于刀座上，如图6所示。

2种刀盘的变形和应力有限元计算结果如图7和图8所示。可以看到： 1)刀盘变形从刀盘中心至外周以近似同心圆的形式减小； 2)刀盘面的变形主要发生在与法兰内孔直径相近的区域，即没有筋板支撑的区域，而外侧有筋板支撑的刀盘区域变形量明显较小。刀盘的高应力主要集中在刀盘中心、滚刀分布密集区与结构尖角处。

(a) 真实刀孔 (b) 模型刀孔

图6载荷施加示意图

Fig. 6 Sketch of loading

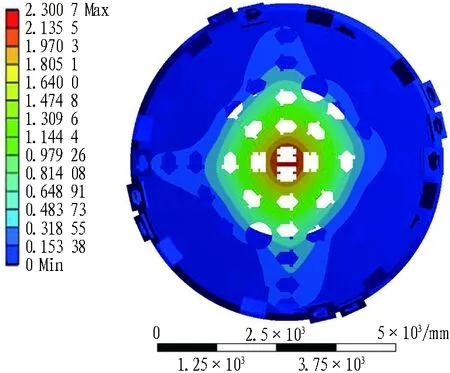
(a) 刀盘变形(单位： mm)

3.3 刀盘变形和应变分布与滚刀分布密度的关联分析

提取刀盘面的变形特征，绘制三维曲面图，如图9所示。可以看到，曲面图的形状与滚刀分布密度曲面图相似，均为中部“山峰”形式。

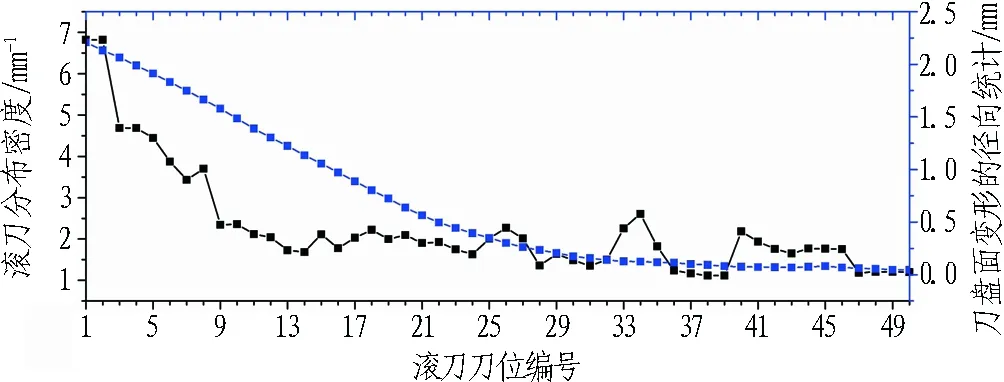
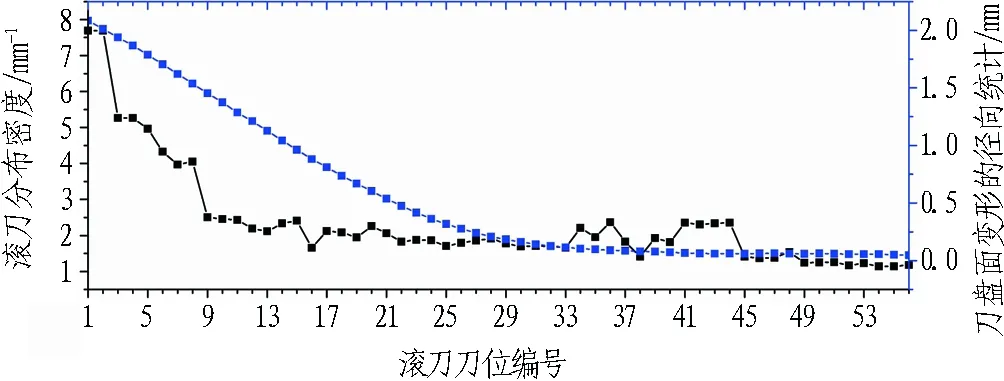
由于刀盘面的变形呈同心圆分布，提取各把滚刀对应极径所包罗的圆环区域上节点的变形量，取其平均值，同时提取N=3时的滚刀分布密度曲线，将二者绘制在同一幅图中，如图10所示。可以看到，滚刀分布密度曲线和刀盘面变形曲线的整体分布形式类似，均为从刀盘中心向外周逐渐减小的形式。对于方案1和方案2中刀号小于20的滚刀，其刀盘面变形曲线明显高于滚刀分布密度曲线，这是由于该区域没有筋板支撑的缘故。

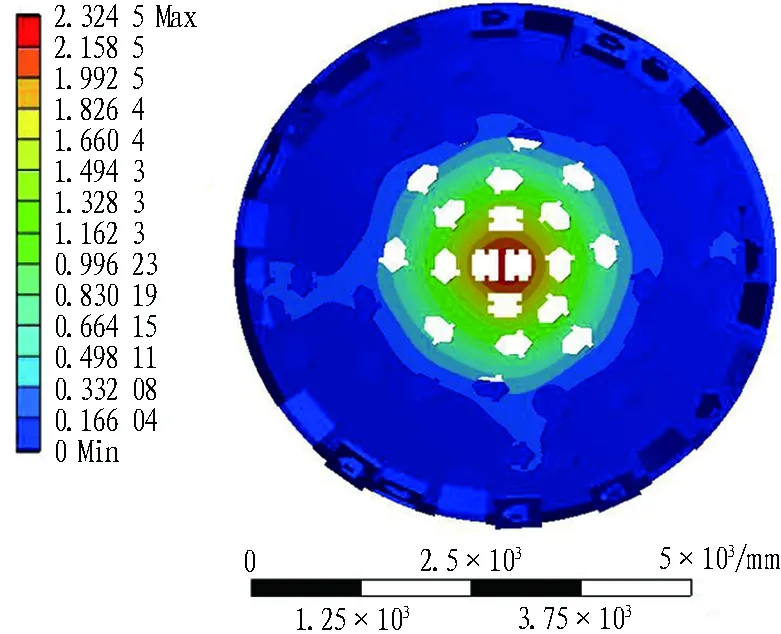
(a) 刀盘变形(单位： mm)

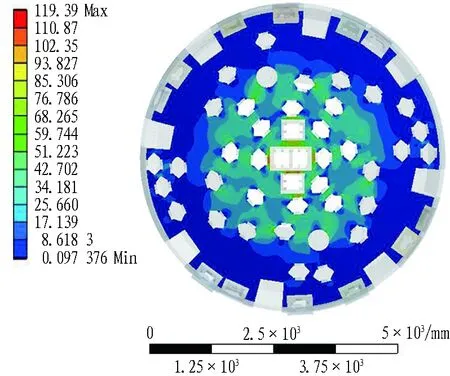
(b) 刀盘应力分布(单位： MPa)

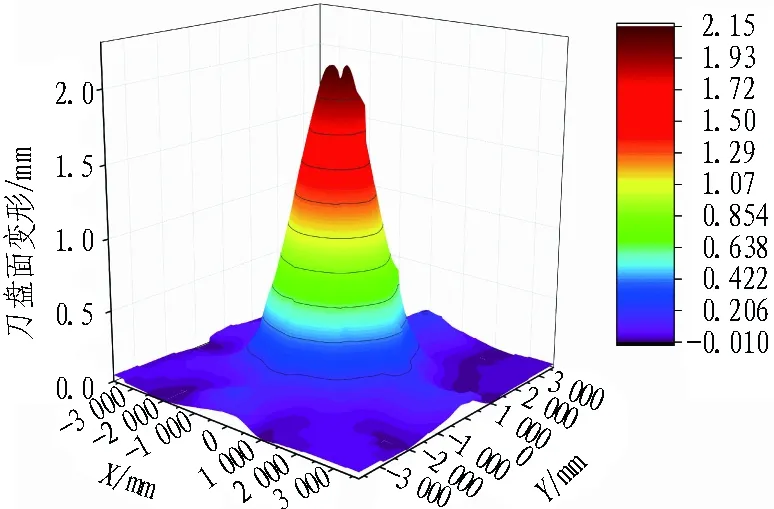
(a) 方案1

(b) 方案2

(a) 方案1

(b) 方案2

Fig. 10 Co-relation between cutter distribution density and cutterhead deformation

对于方案1中编号为25、26、27、33、34、40等刀位，可以看到其滚刀分布密度明显偏大，而由图7(b)可以看到，与这些刀位相对应的刀盘区域的应力也相应偏高，这说明滚刀分布密度的增大会引起相应刀盘区域应力的增大。与之相比，方案2的滚刀分布密度曲线较为平缓，相应的其刀盘应力(见图8(b))也比方案1要小，因而方案2的滚刀布置模式更为理想。

上述分析表明，滚刀分布密度与溜渣板共同影响刀盘面的变形，滚刀分布密度影响刀盘局部的应力分布情况。在实际滚刀布置设计中，应合理地进行溜渣板的布置设计，适当增大刀盘中心区域的滚刀间距，从而减小该区域的滚刀分布密度，并保证全局的滚刀分布密度曲线尽量平滑。

4 结论与建议

本文基于硬岩TBM刀盘的2种滚刀布置设计方案，从刀盘整体受力平衡、刀盘变形和应力分布角度，研究了其滚刀群径向不平衡力、倾覆力矩和质心偏斜量，提出了滚刀分布密度评价指标。主要结论和建议如下。

1)随机式滚刀布置方案的刀盘整体受力平衡效果明显优于米字型布置方案。

2)通过对刀盘的变形和应力进行有限元计算，发现溜渣板在极大程度上影响着刀盘的变形，因而需要重视溜渣板的设计。

3)提出了滚刀分布密度的概念，研究表明，滚刀分布密度可直观反映刀盘的变形和应力，可以作为指导滚刀布置设计的评价指标。实际设计过程中，建议适当增大刀盘内侧滚刀的间距，减小刀盘外侧滚刀的间距，从而使滚刀分布密度曲线整体平缓；同时应尽量使滚刀分布密度曲线光滑，减小局部区域滚刀安装过多而造成的刀盘不良受力。

本文针对相同直径刀盘、不同刀具布置方案进行了对比分析，受到刀座尺寸等因素的影响，导致同等刀盘直径、不同布刀方案布置的刀具数量不同，对分析刀盘受力和变形等会产生一定的影响。后续将进行相同刀具数量下2种布刀方案的刀盘性能对比分析，进一步研究滚刀分布密度对刀盘性能的影响。

：

[1] 张旭辉, 夏毅敏, 谭青, 等. 节理岩体下TBM单刃和双刃滚刀破岩特性研究[J]. 哈尔滨工程大学学报, 2016, 37(10): 1424.

ZHANG Xuhui, XIA Yimin, TAN Qing, et al. Study of the characteristics of breaking jointed rock by tunnel boring machine single-point and double-point cutters[J]. Journal of Harbin Engineering University, 2016, 37(10): 1424.

[2] HUO Junzhou, SUN Wei, CHEN Jing, et al. Disc cutters plane layout design of the full-face rock tunnel boring machine(TBM) based on different layout patterns[J]. Computers & Industrial Engineering, 2011, 61(4): 1209.

[3] HUO Junzhou, SUN Wei, CHEN Jing, et al. Optimal disc cutters plane layout design of the full-face rock tunnel boring machine (TBM) based on a multi-objective genetic algorithm[J]. Journal of Mechanical Science and Technology, 2010, 24(2): 521.

[4] HUO Junzhou, SUN Wei, SU Pengcheng, et al. Optimal disc cutters plane layout design of the full-face rock tunnel boring machine (TBM) using an ant colony optimization algorithm[C]// Proceedings of the 2nd International Conference on Intelligent Robotics and Applications. [S.l.]: ICIRA, 2009: 443.

[5] SUN Wei, HUO Junzhou, CHEN Jing, et al. Disc cutters′ layout design of the full-face rock tunnel boring machine (TBM) using a cooperative coevolutionary algorithm [J]. Journal of Mechanical Science and Technology, 2011, 25(2): 415.

[6] GENG Qi, WEI Zhengying, DU Jun. A cutter layout optimization method for full-face rock tunnel boring machine[C]//Proceedings of the 6th International Conference on Intelligent Robotics and Applications.[S.l.]: ICIRA, 2013: 727.

[7] GENG Qi, WEI Zhengying, HE Fei, et al. Comparison of

the mechanical performance between two-stage and flat-face cutterhead for the rock tunnel boring machine(TBM)[J]. Journal of Mechanical Science and Technology, 2015, 29(5): 2047.

[8] 耿麒, 魏正英, 杜军. 全断面岩石掘进机滚刀布置的优化方法[J]. 西安交通大学学报, 2013, 47(9): 100.

GENG Qi, WEI Zhengying, DU Jun. Cutter layout optimization method of full-face rock tunnel boring machine[J]. Journal of Xi′an Jiaotong University, 2013, 47(9): 100.

[9] 夏毅敏, 林赉贶, 罗德志, 等. 复合式土压平衡盾构盘形滚刀布置规律[J]. 中南大学学报(自然科学版), 2013, 44(9): 3652.

XIA Yimin, LIN Laikuang, LUO Dezhi, et al. Disc cutter layout law for composite EPB shield[J]. Journal of Central South University (Science and Technology), 2013, 44(9): 3652.

[10] 林赉贶, 郭金成, 夏毅敏, 等. 全断面岩石掘进机边缘滚刀优化布置研究[J]. 现代隧道技术, 2016, 53(4): 90.

LIN Laikuang, GUO Jincheng, XIA Yimin, et al. Layout optimization of TBM gauge disc cutters[J]. Modern Tunnelling Technology, 2016, 53(4): 90.

[11] 张照煌, 乔永立. 全断面岩石掘进机盘形滚刀布置规律研究[J]. 工程力学, 2011, 28(5): 172.

ZHANG Zhaohuang, QIAO Yongli. Research on the layout of TBM disc cutter[J]. Engineering Mechanics, 2011, 28(5): 172.

[12] 曹旭阳, 张伟, 王欣, 等. TBM典型刀盘刀具布置方法及软件实现[J]. 工程机械, 2010, 41(1): 21.

CAO Xuyang, ZHANG Wei, WANG Xin, et al. Cutters arrangement for typical cutter disk of a TBM and its software realization[J]. Construction Machinery and Equipment, 2010, 41(1): 21.

[13] ROSTAMI J. Development of a force estimation model for rock fragmentation with disc cutters through theoretical modeling and physical measurement of crushed zone pressure[D]. Golden: Colorado School of Mines, 1997.

[14] 耿麒, 魏正英, 杜军, 等. 基于灰关联分析的全断面岩石掘进机滚刀布局优化方法[J]. 机械工程学报, 2014, 50(21): 45.

GENG Qi, WEI Zhengying, DU Jun, et al. Cutters′ layout optimization method of the full-face rock tunnel boring machine based on grey relational analysis[J]. Journal of Mechanical Engineering, 2014, 50(21): 45.