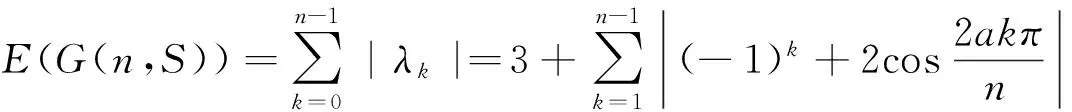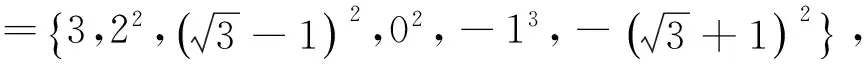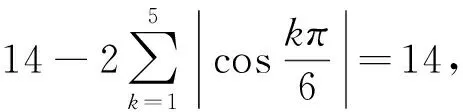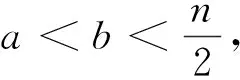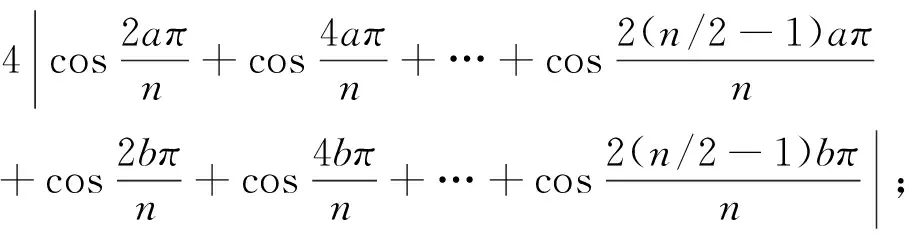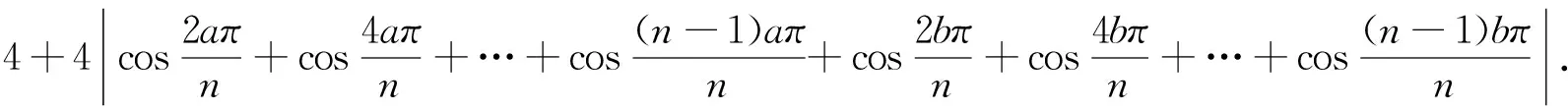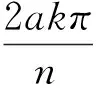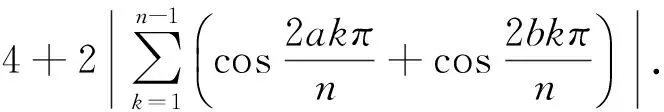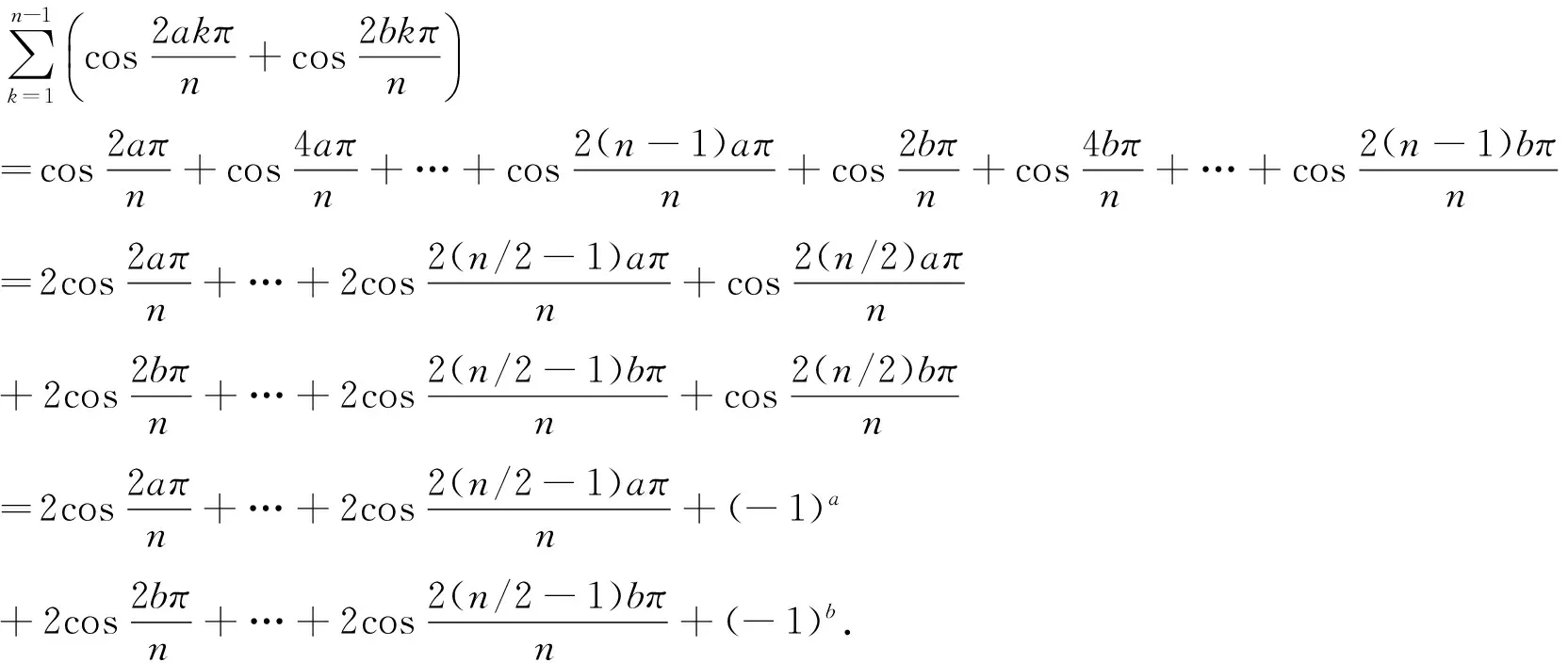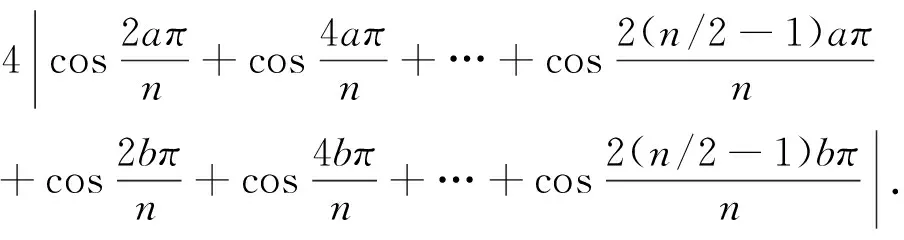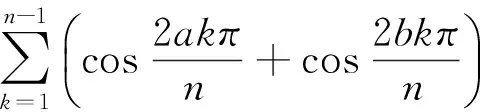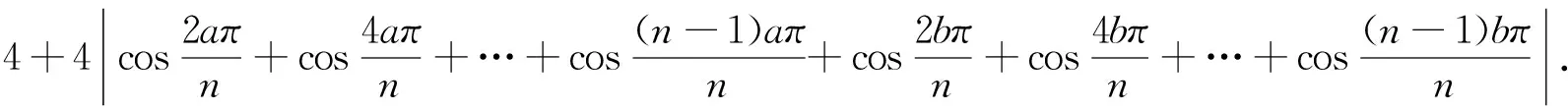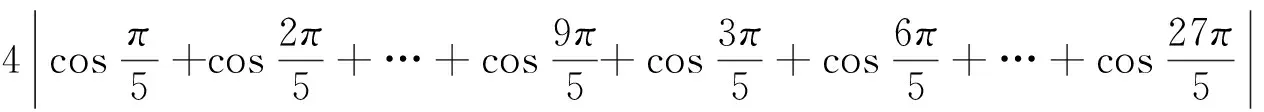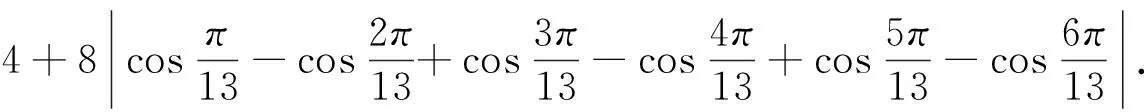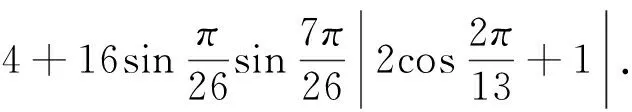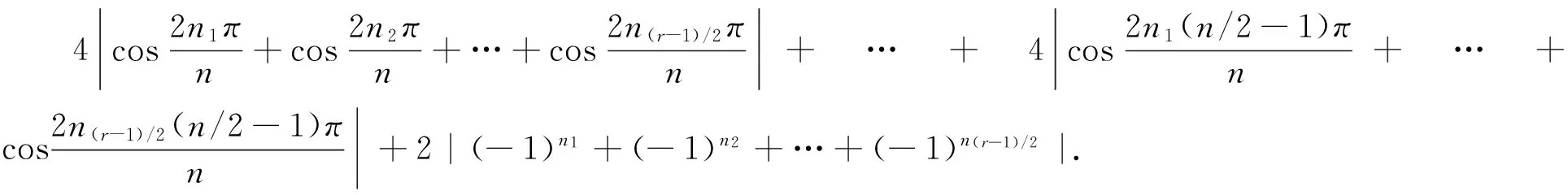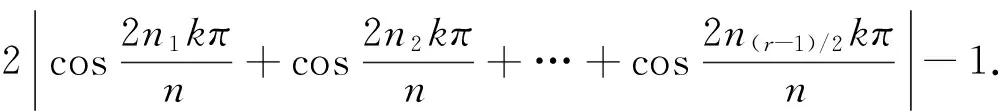某些循环图能量的下界
2018-04-19徐幼专周后卿
徐幼专,周后卿
(1.邵阳广播电视大学,湖南 邵阳 422000;2.邵阳学院 理学院,湖南 邵阳 422000)
图的能量来源于理论化学.20世纪 70年代,著名数学化学家I.Gutman[1]提出了简单图的能量的概念,将能量定义为图的特征值的绝对值之和.化学家在研究共轭的碳氢化合物的性质时,发现总π电能与共轭的碳氢化合物形成时所释放的能量密切相关,而且它过去常常被用来计算共轭烃的共振能量,所得结果和其他较为先进的方法所得到的结果一样好.于是,我们经常会用计算物质的 总π-电子能量来得到它的能量.在理论化学中,六角系统作为苯环的自然表示是一个很重要的图类,它的总π-电子能量是其化学构造和其稳定性的一个桥梁,并且在许多领域都有广泛应用.因此对其拓扑性质中总π-电子能量的研究,不但在理论上而且在实际中也具有重要意义.
π电能的计算最终归结为其分子图的所有特征值的绝对值之和[2-4].图的能量与图的特征值有关,即与图谱有关,图的谱理论与Huckel分子轨道理论之间存在明确的对应关系,如图的谱对应于分子能级,特征向量对应于分子轨道等等.图的能量问题实际上是矩阵(邻接矩阵,拉普拉斯矩阵,距离矩阵等等)的特征值问题,而特征值问题是矩阵理论的一个主要研究对象[5,6],许多科学与工程问题最终都转化成特征值问题来解决.因此,依据矩阵理论来研究图的能量是一个常用的研究方法.循环图是一类重要的图,它具有结构稳定的特点,许多化学分子式就是具有6个顶点的循环图的复制粘合叠加.
1 有关能量下界的一些结论
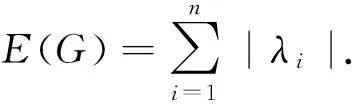
McCLELLAND[10]利用顶点、边和行列式,证明了下列结论:
如果G是一个具有n顶点m条边,邻接矩阵为A的简单图,则G的能量满足

对于二部图,GUTMAN[11]改写了上述下界,获得了下列结果:

CAPOROSSI[12]等人发现了一个简单的下界,只与边有关,他们证明了

DAS[13]等人改进了文献[10]的下界,他们推出了下列结论:
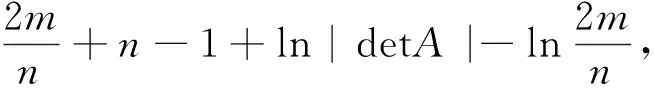
等式成立当且仅当G与完全图Kn同构.
利用矩阵特征值,FATH-TABAR[14]等人给出了下界:
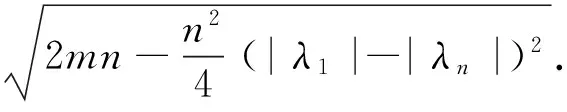
MILOVANOVIC[15]等人获得了下列结果:
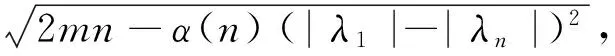
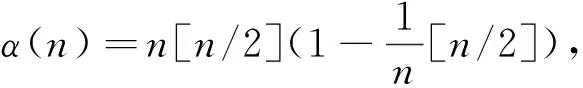
DAS[16]等人在此基础上有所改良,若|λ1|≥|λ2|≥…≥|λk|(kn),他们证明了
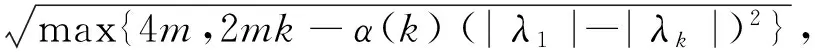
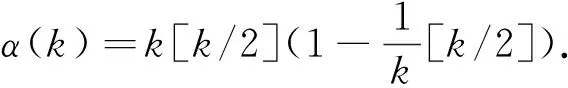
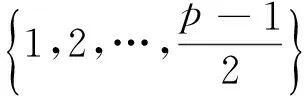
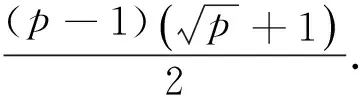
本文研究循环图能量的下界.
2 有关循环图的背景
一个图G称为循环图,如果它的邻接矩阵是一个循环矩阵,它是循环群上的Cayley 图.
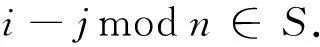
设循环图G(n,S)的邻接矩阵为
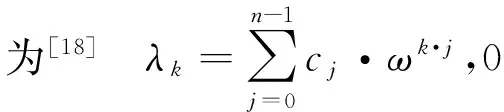
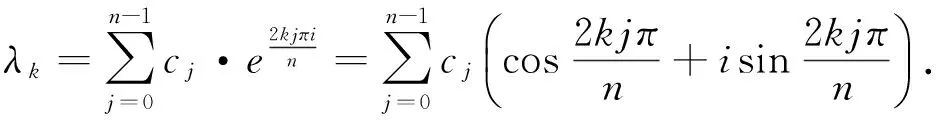
由于A是实对称矩阵,因此A的特征值为实数.从而在(1)式中有
所以,循环图的特征值为
假设S={n1,n2,…,np},ni∈{1,2,…,n-1},则G(n,S)是一个度为p的正则图,因此在c0,c1,…,cn-1中,只有p个元素等于1,其余的均为0.显然c0=0,从而有
(2.1)
其中,n1,n2,…,np分别表示它们在矩阵中所处的列数.
3 定理及证明
下面,我们证明本文的定理.
定理1若G(n,S)是一个具有n个顶点的3-循环图(即3度循环图),则

证明假设G(n,S)是一个具有n个顶点,m条边的3度循环图.由3n=2m可知,n一定为偶数,S的形式一定为S={a,n/2,n-a}(1a 所以, 则 1)当n为偶数时, 2)当n为奇数时, 证明假设G(n,S)是一个具有n个顶点,m条边的4度循环图.由4n=2m可知,n可为偶数也可为奇数.由(2.1)可知,此时的循环图的特征值为 显然λ0=4.于是,我们可推出该循环图的能量 1)当n为偶数时, 从而推出 2)当n为奇数时, 所以, 例如,取n=20,S={2,6,14,18}时,对于循环图G(20,S),直接求得它的特征值谱为Sp(G)={42,18,-18,-42}.所求能量为E(G(20,S))=32. 用定理2来求,则有 显然成立. 若取n=13,S={1,2,11,12}时,对于循环图G(13,S),直接求得它的特征值谱为Sp(G)={4,2.907 02,0.426 92,-0.170 92,-1.256 02,-1.700 82,-2.206 22}.所求能量为E(G(13,S))=21.335 6. 再利用定理2来求, 定理3若G(n,S)是一个顶点为n的r-循环图,S={n1,n2,…,nr},1n1<… 2)当r为偶数时, 证明1)若r为奇数,显然顶点数n必为偶数,则有 n1+nr=…=n(r-1)/2+n(r+3)/2=2n(r+1)/2=n 由(2.1)式有 于是,得到循环图的能量为 2)若r为偶数,n可为偶数也可为奇数.因为n1+nr=…=nr/2+n(r+2)/2=n, 从而,推出循环图的能量为 于是,定理得到证明. 参考文献: [1]GUTMAN I.The energy of graph[J].Ber.Math.Statist.Sckt.Forschungsz.Graz,1978(103):1-22. [2]GUTMAN I,RADENKOVIC S,DORDEVIC S,et al.Totalπ-electron and HOMO energy[J].Chemical Physics Letters,2016(649):148-150. [3]GUTMAN I.Total π-electron energy of conjugated molecules with non-bonding molecular orbitals[J].Zeitschrift für Naturforschung A,2016(71):161-164. [4]GUTMAN I,RADENKOVIC S,DORDEVIC S,et al.Extending the McClelland formula for totalπ-electron energy[J].Journal of Mathematical Chemistry,2017(6):1-7. [5]刘丽波.块复合矩阵之块C-特征向量的若干性质[J].吉林化工学院学报,2014(7):79-81. [6]徐长玲.块特征值的包含域[J].吉林化工学院学报,2015,32(8):50-52. [7]LI X L,SHI Y T,GUTMAN I.Graph Energy[M].New York,Springer-Verlag,2012. [8]MILOVANOVIC I Z,MILOVANOVIC E I,GUTMAN I.Upper bounds for some graph energies[J].Applied Mathematics and Computation,2017(289):435-443. [9]GUTMAN I,FURTULA B.Survey of graph energies[J].Mathematics Interdisciplinary Research,2017(2):85-129. [10] McCLELLAND B J.Properties of the latent roots of a matrix:The estimation ofπ-electron energies[J].The Journal of Chemical Physics,1971(54):640-643. [11] GUTMAN I.Bounds for totalπ-electron energy[J].Chemical Physics Letters,1974(24):283-285. [12] GAPOROSSI G,CVETKOVIC D,GUTMAN I.Variable neighborhood search for extremal graphs.2.Finding graphs with extremal energy[J].Journal of Chemical Information and Computer Sciences,1999(39):984-996. [13] DAS K C,MOJALLALL A,GUTMAN I.Improving McClelland’s Lower Bound for Energy[J].MATCH Communications in Mathematical and in Computer Chemistry,2013(70):663-668. [14] FATH-TABAR G H,ASHRAFI R.Some remarks on Laplacian eigenvalues and Laplacian energy of graphs[J].Mathematical Communications,2010(5):443-451. [15] MILOVANOVIC I Z,MILOVANOVIC E I,ZAKIC A.A short note on graph energy[J].ˇMATCH Communications in Mathematical and in Computer Chemistry,2014(72):179-182. [16] DAS K C,ELUMALAI S.On Energy of Graphs[J].MATCH Communications in Mathematical and in Computer Chemistry,2017(77):3-8. [17] SHPARLINSKI I.On the energy of some circulant graphs[J],Linear Algebra and its Applications,2006(414):378-382. [18] DAVIS P.Circulant Matrices[M].New York,John Wiley & Sons,1979.