基于TOPSIS和递归等权法的中长期负荷组合预测
2018-04-19赵爱芳朱珞敬
李 辉,陈 耀,丁 杰,赵爱芳,朱珞敬
(国网浙江省电力有限公司台州供电公司,浙江 台州 318000)
0 引言
电力系统规划是电力系统快速可靠发展的重要组成部分,而中长期负荷预测是电力系统规划的重要环节,其预测精度与规划方案的质量密切相关[1-3]。如何切实有效地提高中长期负荷预测精度,正逐步进入电力企业视线。此外,考虑到负荷具有社会属性,给预测工作带来了复杂的影响因素,因此,急需深入研究预测方法,解决预测精度不足的问题。
单一预测模型局限于固定的适用范围,难以应用于所有情况;相反,组合多个单一模型的预测结果,能够有效克服这种问题,提高预测精度[4-5]。目前,常用的组合方法有最小方差法、方差-协方差法、递归等权法和层次分析法等[6-9]。此外,众多文献提出了组合方法的改进及创新。文献[10]充分考虑电力需求与未来经济发展的关系,提出基于2个评价指标来计算各单一预测模型的权重。文献[11]引入理想点多属性决策算法,建立中长期负荷组合预测模型。文献[12]利用新鲜度函数和预测有效度的模糊自适应变权重建立组合模型,有效避免了组合模型中出现负权重的问题。文献[13]基于粗糙集理论与D-S证据理论建立多元回归分析法组合预测模型。
以下基于前人研究,采用TOPSIS(逼近理想点法)和递归等权法建立组合模型,以单一预测模型各个年份拟合的相对误差绝对值的倒数为属性集,单一预测模型的种类为方案集,通过TOPSIS筛选参与组合模型,利用递归等权法确定参与组合模型的权重,通过算例验证所提模型的实际应用价值。
1 TOPSIS法和递归等权法
1.1 TOPSIS算法原理
TOPSIS法又称逼近于理想解的排序方法,借助多属性问题的正理想解和负理想解给各方案进行排序[14]。所谓正理想解代表各方案中最佳方案,而负理想解则是各方案中的最差方案,其算法思想是先确定每个属性值的正理想解和负理想解,再求出各个方案与最佳方案及最差方案之间的加权欧氏距离,并据此确定方案集中各方案的优先顺序。若设属性集和方案集分别为X=[X1,X2, …,Xm]和 U=[U1,U2, …,Un],aij为方案 Ui按属性Xj进行测度得到的属性值,其具体建模步骤如下:
(1)由方案集和属性集建决策矩阵 A=(aij)n×m。
(2)为了消除不同物理量纲对决策结果的影响,决策时可根据式(1)将 A 规范化为 R=(rij)n×m。
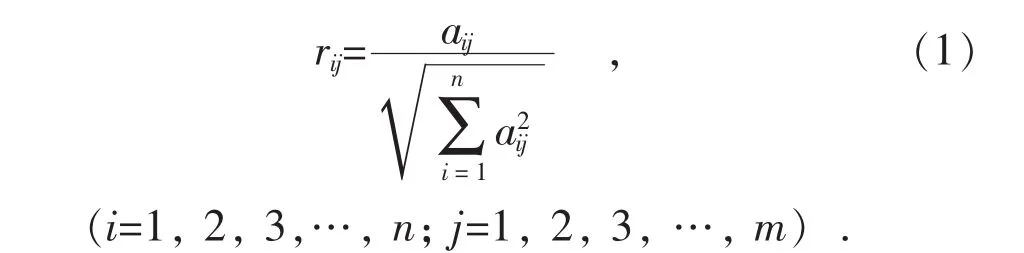
(3)构造加权规范化矩阵 Z=(zij)n×m。 若设各属性给定的权重为 W=[w1, w2, ..., wm], 则 zij=wj×rij。
(4)确定正理想解和负理想解。设正理想解z*的第j个属性值为,负理想解z0第j个属性为, 当属性为效益型时, 正理想解=max(z1j, z2j,..., znj), 负理想解=min(z1j, z2j, ..., znj)。
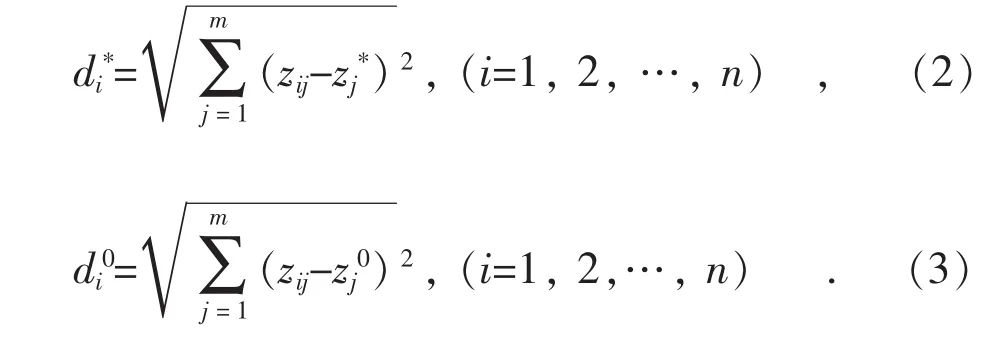
(6)计算各方案的综合评价指数Ci如式(4)所示,按Ci由大到小排序方案的优劣次序:
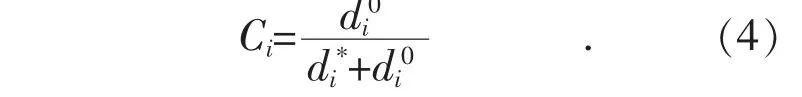
1.2 递归等权法
递归等权法具有简单、方便、组合效果优等特点。原理是对给定的n种预测模型进行简单平均组合,利用组合模型替换原n种模型中预测误差平方和最大的预测模型。继续进行简单平均组合,并做类似替换,直到达到设定次数或预测误差平方和达到设定值停止。具体步骤如下:
对式(5)所示n种预测模型,先进行简单平均组合,其形式记法为式(6),实际含义为式(7):
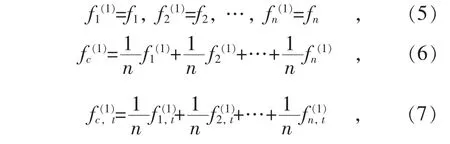
假设第i种预测模型在第一轮组合中误差平方和最大,则用组合模型fc(1)替换掉第i种模型进行第二轮平均组合,其预测值为:
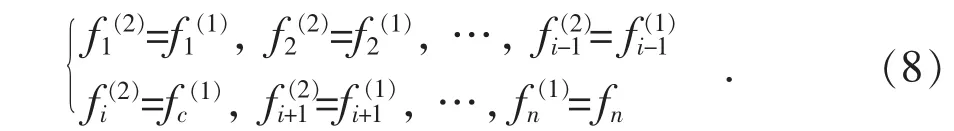
以此类推,经过l轮平均得到组合模型为∶
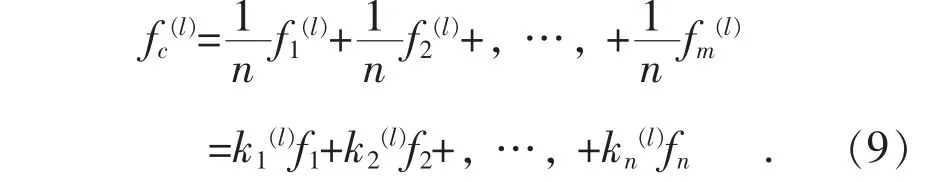
当fc(l)的预测误差平方和改进不大时,停止迭代,确定各模型的最终权重,否则继续迭代直到设定值停止。
2 组合模型的建立
组合原理是基于预测对象f的n种预测模型建立一个对f的综合预测结果。若用fit(i=1,2,…,n)表示第i种预测模型对t时刻的预测值,单一预测模型权重用w=[w1,w2,…,wn]T表示且满足式(10),则第t个时刻最终预测模型表达式如式(11)所示:
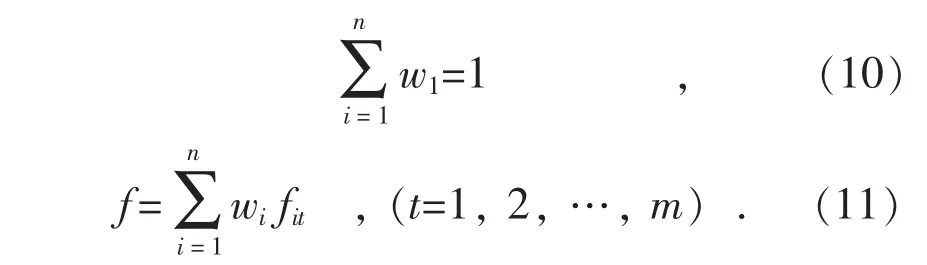
中长期负荷预测过程中,相应年份拟合的相对误差是反映各单一预测模型在该年份拟合精度的重要评价指标,综合各个年份的相对误差是反映模型整体拟合精度的关键。如何选取单一预测模型确定各单一模型的权重是组合的关键,以下利用TOPSIS法综合各年份拟合的相对误差筛选参与组合的单一模型,以递归等权法确定各单一模型的权重,其具体建模步骤如下:
(1)单一预测模型各个年份拟合的相对误差绝对值的倒数为属性集,取倒数目的是将属性类型设为效益型。用每个预测模型种类作为方案集。根据1.1小节步骤(1)和(2)建立A和R。
(2)确定各属性类型的权重。为了突出每个属性对方案集的影响,计算各方案集在该属性下的平均测度为aj′,以各属性平均测度在总平均测度的比重作为各属性类型的权重,计算公式为:

(3)根据 1.1 小节步骤(4)—(6)对各个预测模型进行排序,筛选参与组合的模型。
(4)利用递归等权法确定参与组合模型的权重。
3 算例分析
历史数据选取文献[15]中某省1998—2004年全省用电量,单一预测模型选取S型曲线模型、幂函数模型、人工神经网络模型、双曲线模型、Compertz模型、线性模型和对数模型共7种模型,分别以M1—M7进行编号,拟合的评价指标选取相对误差、MAPE(平均绝对百分比误差)、RMSE(均方根差);7种模型1998—2004年的拟合值如表1所示,拟合相对误差如表2所示。
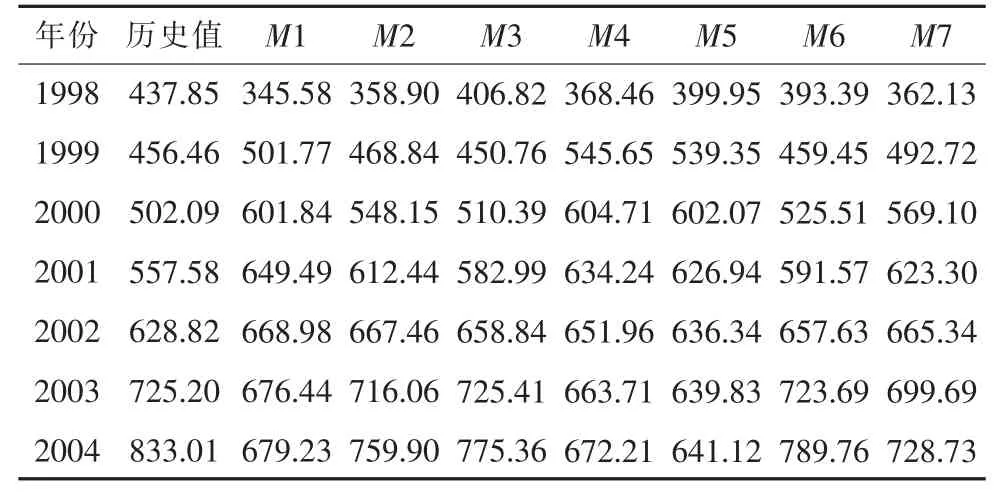
表1 7种单一模型1998—2004年拟合值108kWh
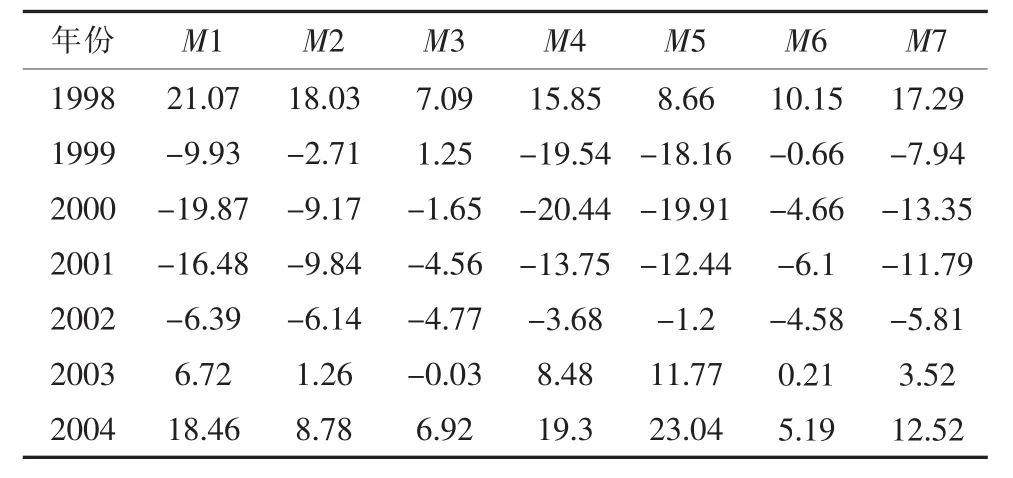
表2 7种单一模型拟合相对误差%
根据表2相对误差,利用1.1小节TOPSIS的建模步骤(1)和(2)建立决策矩阵 A,并以式(1)进行规范化建立R,如式(13)所示。根据式(12)计算各属性的权重为W=[0.01,0.06,0.02,0.02,0.04,0.83,0.01],根据 W 和 R计算 Z,如式(14)所示,根据1.1小节步骤(4)设定:
正理想点为 x+=[0.059 82,0.216 06,0.018 308,0.013 55, 0.039 044, 5.518 006, 0.009 92]。
负理想点为 x-=[0.020 13, 0.001 746, 0.001 478,0.003 694, 0.006 456, 0.003 652, 0.002 25]。
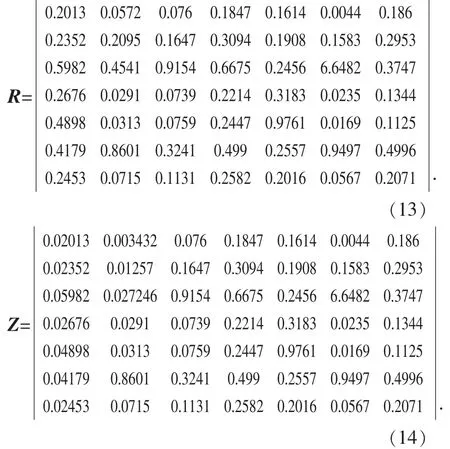
根据1.1小节步骤(5)和(6),得到正理想解欧式距离、负理想解欧式距离、综合评价指标及各方案集排序,如表3所示。
根据表3排序选取排名靠前的4个模型参与组合。将4种模型进行第一轮简单等权组合,即各模型初始权重取0.25,计算各模型最小拟合误差平方和进行比较,用前一轮组合模型替换掉预测误差平方和最大模型,逐步迭代计算,其迭代过程中误差平方和的变换趋势如图1所示。由图1可知,从第20次迭代开始误差平方和基本相等,取第34次迭代的数值作为最终的迭代次数,可求得预测误差平方和为5 934.5,其值与第35次迭代相同,停止迭代。计算此时各模型的权重分别为0.000 3,0.974 4,0.025 1,0.000 2。 根据权重进行组合预测并对组合模型以M8编号,预测结果表4所示。
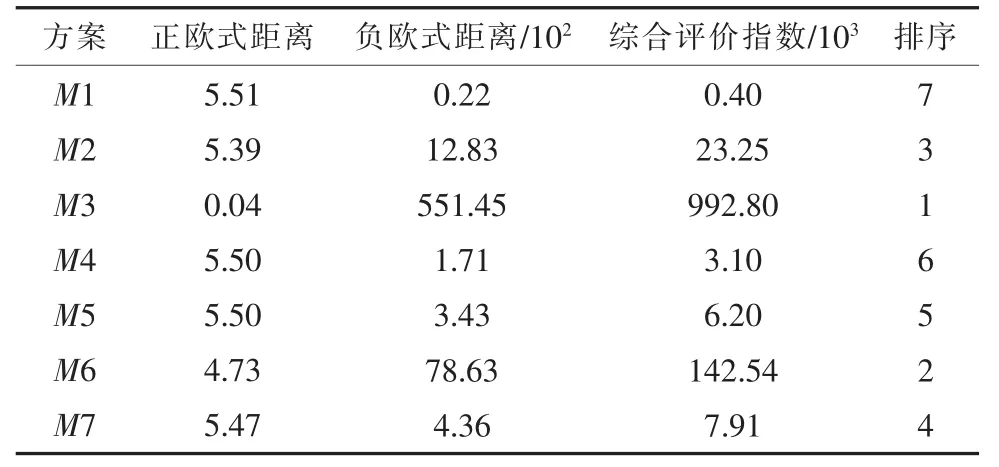
表3 单一模型筛选相关参数
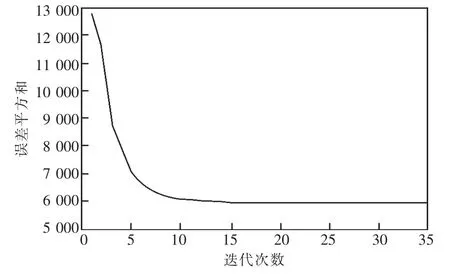
图1 误差平方和与迭代次数关系
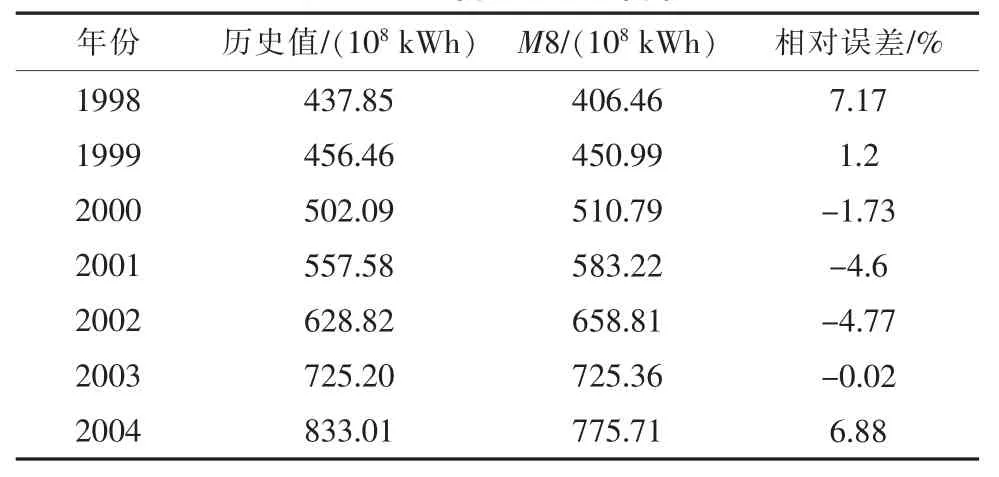
表4 组合模型拟合值
根据表4计算组合模型的MAPE和RMSE分别为 3.77%和 29.12×108kWh,M1—M8模型的MAPE和RMSE如图2、图3所示。由图可知,单一模型中最优拟合模型为M3模型,与M3相比较,M8的MAPE和RMSE与其基本相等,除M3外,M8模型MAPE和RMSE优于其他单一模型,考虑到神经网络M3模型可能具有过拟合的缺陷,而组合模型能有效克服这一缺陷。
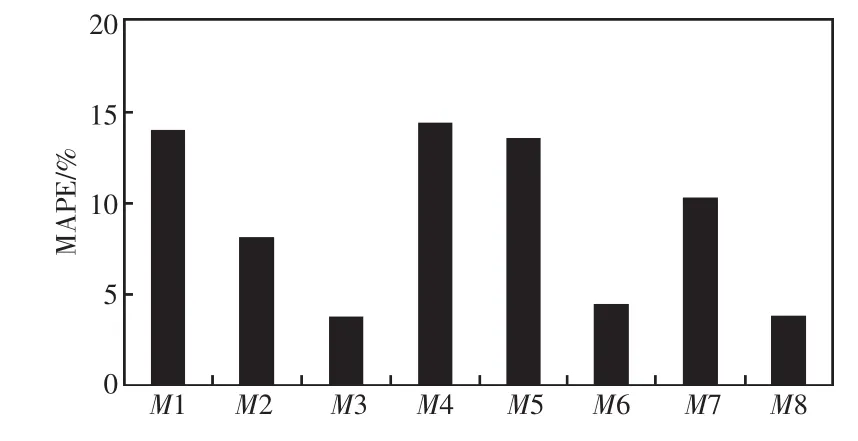
图2 MAPE分析
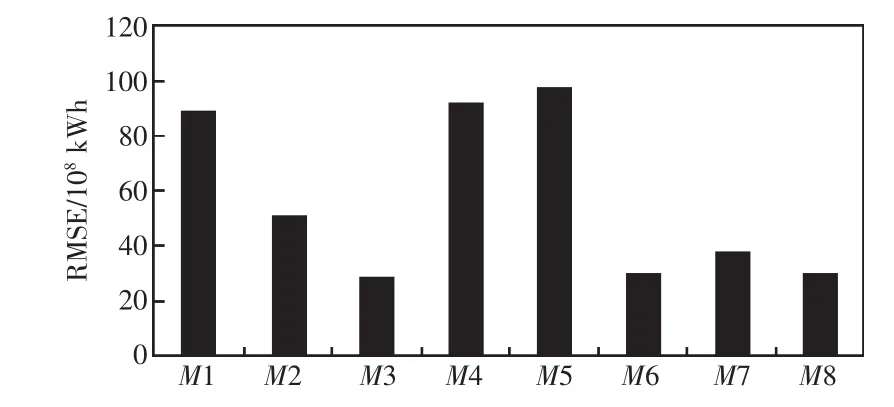
图3 RMSE分析
利用单一模型和组合模型预测2005年的全省用电量,其中2005年全省用电量实际值为946.33×108kWh,8种模型的预测值和相对误差如表5所示。由表5可知,组合模型预测精度与M6相近,除该模型外,组合模型预测精度优于其他模型。考虑到单一模型M1—M7具有适用性有限、获取信息不足以及过拟合等缺陷,组合模型结合单一模型的优缺点取长补短,能够提高预测的可信度。又由于未来负荷的波动性及不确定性,单一模型无法剖析负荷特性,相反组合模型可以综合利用单一模型最大限度地获取负荷的变化特性,具有较强的实用性和可操作性。
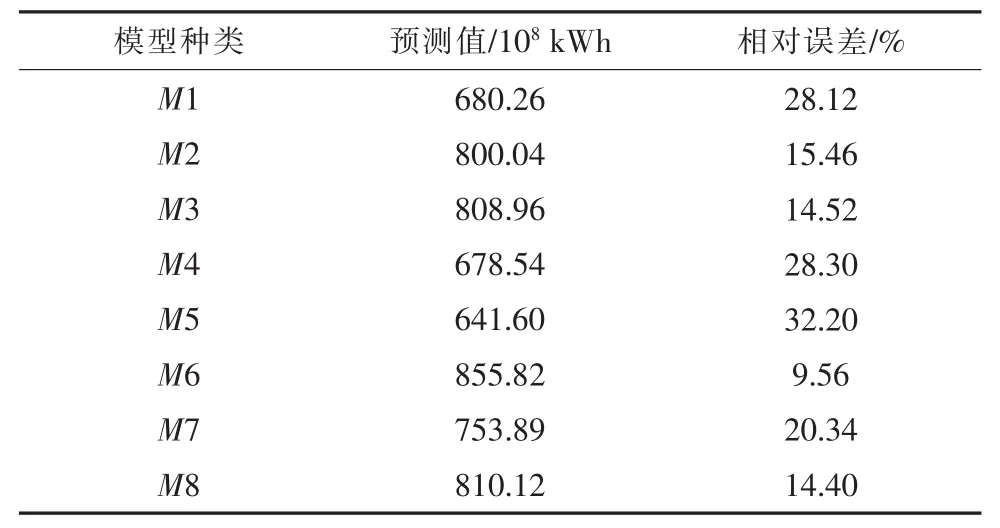
表5 各模型2005年预测值
4 结论
(1)以单一预测模型各个年份拟合的相对误差绝对值倒数为属性集、预测模型种类为方案集,利用TOPSIS法建立筛选模型,该筛选模型有效综合了各个年份的预测精度,提高了筛选的可靠性和有效性。
(2)用递归等权法确定参与组合模型的权重,并通过某省用电量数据进行预测,预测结果表明,所提模型不但具有较高的预测精度和可信度,而且实用性、可操作性更强。
(3)所建模型只是选取各年份拟合的相对误差绝对值倒数为属性集,实际预测中可以进一步扩增属性集提高预测精度。
参考文献:
[1]毛李帆,江岳春,龙瑞华,等.基于偏最小二乘回归分析的中长期电力负荷预测[J].电网技术,2008,32(19)∶71-77.
[2]李辉.用马尔可夫法改进残差GM(1,1)模型中长期负荷预测[J].陕西电力,2017,45(5)∶75-77.
[3]杨胡萍,李辉.基于Adaboost的改进多元线性回归算法中长期负荷预测[J].太原理工大学学报,2017,48(5)∶818-821.
[4]王栋,邵常宁,费建平,等.基于大客户和地方电厂数据管理预测平台的负荷还原预测方法研究[J].浙江电力,2015,34(12)∶11-15.
[5]李春祥,牛东晓,孟丽敏.基于层次分析法和径向基函数神经网络的中长期负荷预测综合模型[J].电网技术,2009,33(2)∶99-104.
[6]蒋燕,王少杨,封芸.基于递归等权组合模型的中长期电力负荷预测[J].电力系统及其自动化学报,2012,24(1)∶151-155.
[7]牛东晓,曹树华,卢建昌,等.电力负荷预测技术及其应用[M].北京:中国电力出版社,2009.
[8]贺辉.电力负荷预测和负荷管理[M].北京:中国电力出版社,2012.
[9]张栋梁,严健,李晓波,等.基于马尔可夫链筛选组合预测模型的中长期负荷预测方法[J].电力系统保护与控制,2016,44(12)∶63-67.
[10]温青,张筱慧,杨旭.基于负荷误差和经济发展趋势的组合预测模型在中长期负荷预测中的应用[J].电力系统保护与控制,2011,39(3)∶57-61.
[11]杨胡萍,李辉,占思凯,等.基于理想点多属性决策算法的中长期电力负荷组合预测[J].燕山大学学报,2017,41(1)∶63-67.
[12]孙广强,姚建刚,谢宇翔,等.基于新鲜度函数和预测有效度的模糊自适应变权重中长期电力负荷组合预测[J].电网技术,2009,33(9)∶103-107.
[13]陈毅波,郑玲,姚建刚.基于粗糙集理论与 D-S证据理论改进的多元回归负荷预测方法研究[J].电力系统保护与控制,2016,44(6)∶62-67.
[14]张锦爱.基于法的电网规划方案评估[J].安徽电力,2013,30(3)∶32-34.
[15]康重庆,夏清,刘梅.电力系统负荷预测[M].北京:中国电力出版社,2007.
[16]雷涛,吕勇.马淑慧.基于改进灰色理论的主动配电网中长期负荷控制[J].电网与清洁能源,2016,32(9)∶22-28.
[17]李辉.改进残差GM(1,1)模型在中长期负荷预测中的应用[J].广东电力,2017,30(9)∶81-85.
