基于复杂网络理论的系统脆弱度评估新方法

陈伟华，王 刚，叶仁杰，张 浩，刘 倩

（1.国网浙江省电力有限公司台州供电公司，浙江 台州 318000；2.强电磁工程与新技术国家重点实验室（华中科技大学），武汉 430077；3.华中科技大学同济医学院附属协和医院，武汉 430022）

0 引言

近几年，电力系统大停电事故受到越来越多的关注[1－3]。传统的电力系统研究主要是基于还原论思想，在将电力系统各元件建成的精确数学模型的基础上，将电力系统描述成一组巨维的微分代数方程，最后通过计算机仿真技术求解电力系统的运行状态。由于现代电力系统庞大的规模和复杂的特性，传统的还原论方法在深入分析电力系统的安全稳定研究中已经暴露出明显的不足。

复杂网络理论强调用整体论和还原论相结合的方法来分析系统，将个体及其相互作用或用演化的结构抽象成网络的节点和边，认为结构决定系统的功能，是研究复杂系统的一种新方法。电力系统作为典型的复杂系统，是复杂网络理论的重点研究对象。应用复杂网络理论为研究复杂电力系统提供了一个新的研究角度和方法，它关注电力系统中各组成部分相互关联作用的拓扑结构，从网络结构层面分析电力系统内在的、本质的特性。

早期引入复杂网络理论的电力系统研究，将系统抽象为无向无权网络[4-6]，这些研究忽略了实际电力系统本身的物理特性，不太适用于实际电力系统的定量计算和分析。因而，此后的研究中注重将电力系统本身的特性引入到复杂网络模型的研究中，将电力系统抽象成为加权网络。比较常见的改进方法是引入电气变量作为抽象模型的边的权值，这些电气变量包括：线路电抗值[7-9]、线路传输的有功功率[1，10-11]、网络拓扑失效时间概率[12]。

经典的复杂网络理论假设信息或能量沿着最短路径在节点间传播，当前部分基于复杂网络理论的电力系统研究仍采用这一假设，假设电力系统中的电能在节点间的传播是通过最短路径进行的[8，12-15]。然而这一假设并不符合电力系统的实际物理特性，电力系统中的电能并不是按照最短路径传播，而是满足基尔霍夫定律，沿任意可能的输电通道传播。为了避免在电力系统研究中使用最短路径概念，学者们提出了多种节点间电气距离的定义，其中文献[16]利用电压无功灵敏度矩阵将元素转换为节点间电气距离，文献[17]采用节点间的戴维南等值导纳来衡量节点间的电气距离，文献[18]使用节点间等值阻抗来描述节点间的电气距离。

当前，基于复杂网络的电网脆弱性研究绝大部分只考虑电力系统网络拓扑结构的影响，然而电力系统的安全稳定不仅与网络拓扑结构有关，也与当前的运行状态密切相关。因此，结合网络拓扑和运行状态成为了当前基于复杂网络的电力系统研究工作的趋势。文献[10]提出的指标综合考虑了线路的权重和功率传输，从全局有功功率传输和局部无功功率平衡2个层面衡量线路的脆弱性。文献[11]提出的静态重要度指标，基于复杂网络的介数概念，同时考虑系统当前的负荷水平。

以下结合电力系统网络拓扑和运行状态，提出了一种新的线路脆弱度指标，能快速有效地评估线路故障的严重性。

1 线路脆弱度评估指标参数

1.1 等效平均电气距离[18]

电力系统中节点间的电气距离表征了节点间的电气耦合关系，仅仅采用经典复杂网络理论的两点间最短路径所包含边的数目来表示，是不符合电力系统物理规律的。电力系统中电能的传播符合基尔霍夫定律，线路中传输的功率与线路的阻抗有关，采用节点间的等效阻抗来表征节点间的电气距离更符合电力系统的物理规律。同时线路阻抗只是电力系统固有参数，还不能反映出电力系统的运行状态。

电力系统节点i和j之间的等效电气距离可以定义为两点之间等值阻抗Zij，equ，数值上等于从节点i注入单位电流后节点i与j之间的电压Uij。由叠加原理（见图1）可以推得Zij，equ可以用系统节点阻抗矩阵元素表示：

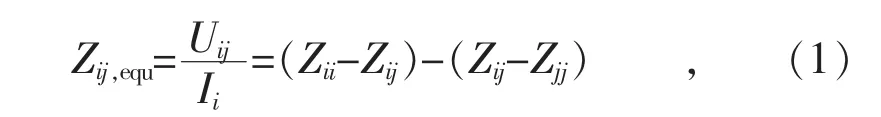
式中：Ii为节点的输入电流；Zii为节点i自阻抗；Zij为节点i和节点j的互阻抗；Zjj为节点i自阻抗。

图1 节点间等效电气距离计算原理

类似于经典复杂网络参数特征路径长度，电力系统网络的等效平均电气距离可以定义为所有节点对的等效电气距离的平均值：

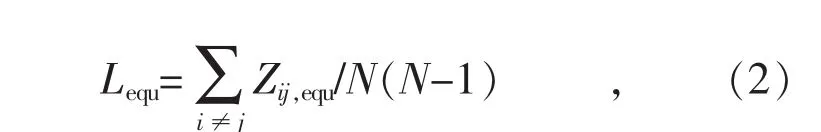
式中：N为节点总数；Lequ为系统等效平均电气距离。

由小世界理论[19-21]可知，系统节点间的平均距离越近，小世界特性越明显，从而系统在遇到故障后，故障传播的广度越大，系统呈现的脆弱性越大。

1.2 加权传输功率容量利用率

文献[10]的全局性指标平均传输距离是基于加权网络的参数传输路径加权长度之和LT，该参数定义为所有传输路径的权重和长度的乘积之和。文献[10]通过推导，将传输路径加权长度之和转换为线路的加权长度之和：

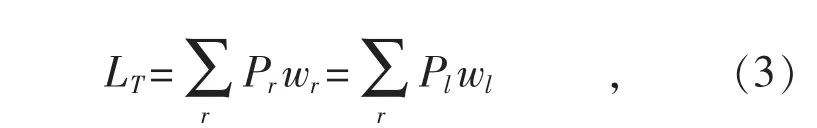
式中：r为任意一条传输路径，取值范围为传输路径集合R；l为任意一条传输线路，取值范围为加权网络的线路集L；wl为线路l的长度，即线路电抗；pl为线路l的权重，即传输的有功功率。

线路的加权长度之和表征了系统传输功率的效率，如果故障导致LT大幅增加，表明故障线路附近没有可替代的有功功率传输通道，有功功率不得不在系统中大范围迁移。然而对于低载线路，即使在功率转移后，线路的传输功率增加较多，但未超过线路功率输送限制，并不会影响线路的安全运行；对于重载线路，功率转移后，即使线路的传输功率增加不多，但接近或超过了线路传输功率输送限制，则会影响线路的安全稳定运行，并可能引发系统的连锁故障，威胁系统的安全稳定。因此，采用线路的加权长度之和并不能直观表示线路的脆弱程度，而线路输送的功率越接近线路的功率输送极限，线路的脆弱度越高，所以采用线路传输功率容量利用率（线路输送的有功功率与输送功率极限的比值）代替线路传输有功功率能更好地表征线路的脆弱程度。按照这个思路，改进文献[10]中线路的加权长度之和指标，可以用加权传输功率利用率Lp来表征系统的脆弱度：

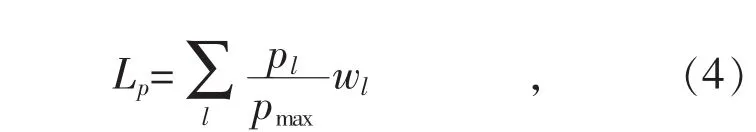
式中：pmax为线路的输送功率极限。

1.3 线路脆弱度指标

为评估线路故障后对系统全局安全稳定的影响，采用一种新的指标来衡量线路脆弱度。

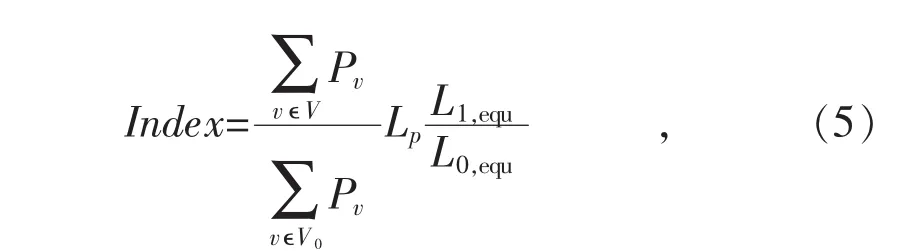
式中：L1，equ为线路故障后的等效平均电气距离；L0，equ为线路故障前的等效平均电气距离；Pv为节点v吸收的有功功率；V为线路故障后所有节点集合；V0为故障前所有节点集合。

加权传输功率容量利用率Lp表征了线路故障后的系统脆弱度；等效平均电气距离因子L1，equ/L0，equ表征了线路故障后系统等效平均电气距离的变化率，线路故障会增大电力系统等效平均电气距离，若该因子越大，由小世界理论[4，6]可知，该线路在正常运行时将会更大程度地起到减小网络特征路径长度的作用，表明该线路故障对电力系统拓扑结构的影响越大，电力系统越脆弱；系统负荷水平因子表征了线路故障后系统总负荷水平变化，由自临界理论的OPA（直流潮流停电）模型[11]可知，不同负荷水平电网遭受攻击表现出来的脆弱度不同，系统负荷水平越高，系统面临的风险越高。

2 系统脆弱度评估方法

本节利用新的输电线路脆弱度来筛选严重故障，能更好地反映系统脆弱程度，可以实时筛选出当前工况下最严重故障。具体步骤如下：

（1）初始化 i=1。

（2）利用直流潮流算法计算出系统功率分布，并通过系统的导纳矩阵取逆求得系统的阻抗矩阵。

（3）利用式（2）—（5）计算线路故障后系统脆弱度指标。

（4）令 i=i+1。 如果 i＞Nline（Nline为输电线路数目），计算完成；否则，转入步骤（2）。

3 仿真分析

本节采用IEEE 118节点系统作为测试系统，按上述评估方法的步骤，计算出各线路故障后的系统脆弱度指标。线路脆弱度指标由大到小排序，结果见表1，其归一化分布情况如图2所示。

由图2可知，线路故障后系统的脆弱度指标归一化值在0.5以上的线路只有2条，在0.1以上的线路只有12条，表明系统中只有少部分线路故障才会引起系统较严重的稳定问题。

为了说明线路故障后加权传输功率容量利用率Lp与等效平均电气距离因子Lequ/L0，equ之积能更有效地反应线路故障对网络拓扑的影响，提高线路脆弱性的辨识度，本节给出了加权传输功率容量利用率Lp的排序结果（见表2），以及考虑等效平均电气距离因子的指标 Lp（Lequ/L0，equ）的排序结果（见表 3）。

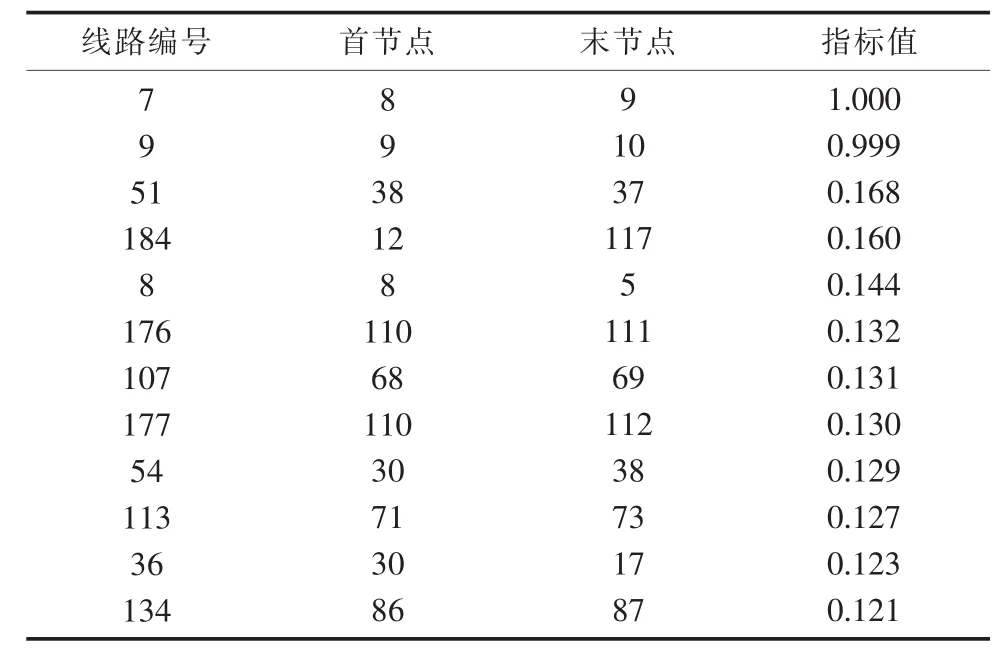
表1 线路脆弱度指标的筛选结果

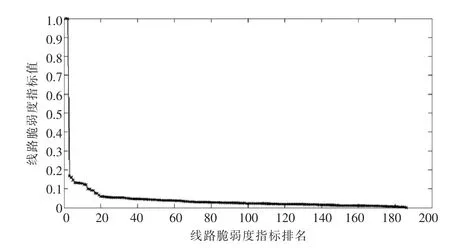
图2 IEEE 118节点系统脆弱度指标归一化分布情况

表2 加权传输功率容量利用率Lp的排序结果

由表2和表3可得，线路7和9故障后，两者加权传输功率容量利用率Lp指标相同，然而两者考虑等效平均电气距离因子的指标 Lp（L1，equ/L0，equ）略有差异。同时线路184和177等故障后，等效平均电气距离因子 L1，equ/L0，equ的值比较大， 两者考虑等效平均电气距离因子的指标 Lp（L1，equ/L0，equ）指标值较大，因此系统脆弱度排序变得较前。

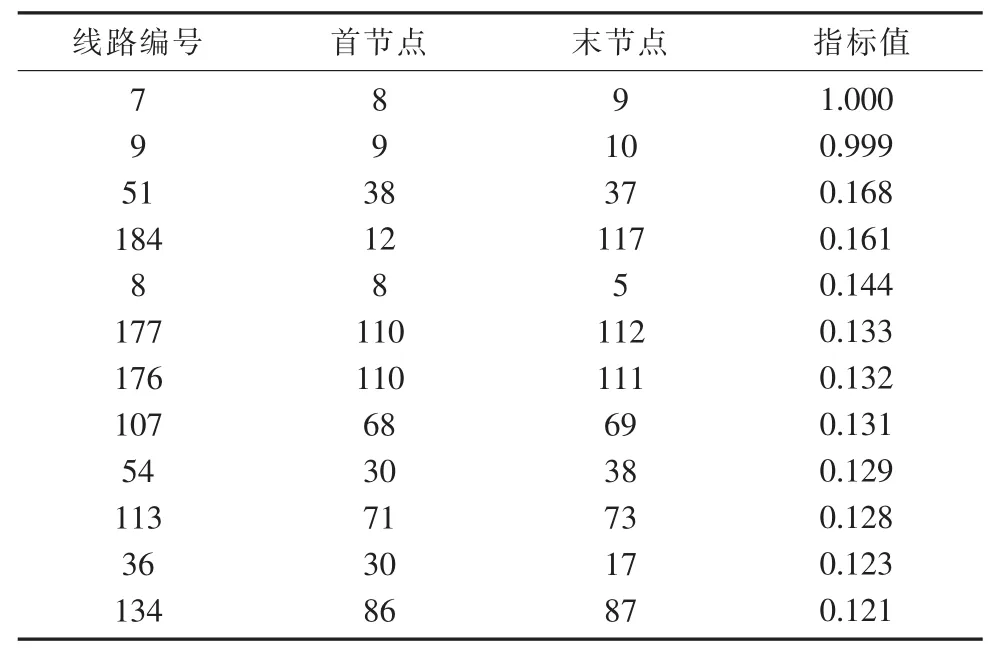
表3 考虑等效平均电气距离因子的指标Lp（Lequ/L0，equ）的排序结果

为进一步说明指标的有效性，将文中所提新指标其与文献[10]的全局性指标平均传输距离进行了分析与比较，详见表4。

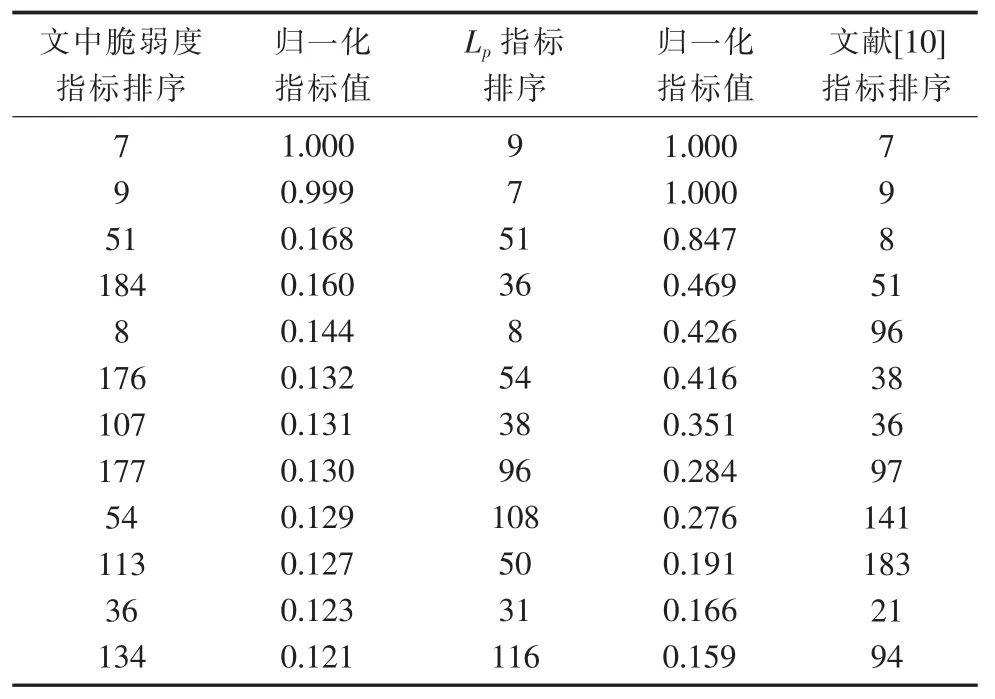
表4 线路脆弱度指标比较

（1）文中所述脆弱度指标Index和加权传输功率容量利用率Lp具有相似性。比如线路7，9，51同时对应着较大的脆弱度指标和加权传输容量利用率指标，这说明当线路传输功率接近其传输容量时，此线路将成为系统的脆弱环节。

（2）文中所提出的脆弱度指标Index考虑系统负荷水平及小世界特性，其不仅能聚焦线路本身传输容量利用率的影响（局部），也能考虑系统层级的网络结构及运行状态变化（全局），从而更好地筛选出脆弱线路，性能指标优于加权传输功率容量利用率Lp，从表4及IEEE 118节点系统图可以看出，利用脆弱度指标Index可以筛选出连接着重要发电机与负荷节点的184，177，176等线路，与线路7和9类似。

（3）文献[10]中全局指标排序较前的线路与文中加权传输功率容量利用率Lp排序比较相近，同时有些差异，表明这2个指标存在内在的相通性。由于前者只考虑线路的功率的加权和，并没有考虑线路的功率输送极限，不能完整体现线路的脆弱程度，而文中所提加权传输功率容量利用率Lp相较而言更加合理。同时文中所述线路故障系统脆弱度指标完整考虑了系统的负荷水平、系统的小世界特性，能更好地反映系统的脆弱程度。由IEEE 118节点系统连接图可知，线路184，177，176等连接着电力系统中重要发电机与负荷节点，与线路7和9的情况类似，而文献[10]并未有效找出这些脆弱线路，由此可以说明文中所提出指标的合理性和完整性。

4 结语

衡量系统脆弱性时，综合考虑系统的负荷水平、系统的运行状态和电力系统网络特征是当前电力系统线路脆弱度评估的趋势。文中提出的指标综合考虑了系统的负荷水平、网络的小世界特性以及线路的功率利用率，能很好评估线路故障后对电力系统静态安全稳定的影响。此外，文中以IEEE 118节点为测试系统，验证了指标和评估方法的有效性，并与当前常用的一种评估方法进行比较分析，验证了所提指标能更有效、全面地评估线路故障对电力系统安全稳定的影响。

后续可以进一步研究一套有效衡量电力系统脆弱程度的指标，定量地反映电力系统面临的脆弱情况。

参考文献：

[1]徐林，王秀丽，王锡凡.电气介数及其在电力系统关键线路识别中的应用[J].中国电机工程学报，2010，30（1）∶33－39.

[2]邓晖，黄弘扬，楼伯良，等.浙江多馈入交直流混联电网电压稳定性分析[J].浙江电力，2017，36（4）∶1－4.

[3]凌卫家，孙维真，叶琳，等.浙江交直流混联电网特性分析及运行控制[J].浙江电力，2016，35（9）∶8－14.

[4]丁明，韩平平.基于小世界拓扑模型的大型电网脆弱性评估算法[J].电力系统自动化，2006，30（8）∶7－10.

[5]ALBERT R，I ALBERT，G L NAKARADO.Structural vul nerability of the North American power grid[J].PHYSICAL REVIEW E，2004，69（1）∶2－6.

[6]ROBERTS J M.Small worlds∶The dynamics of networks between order and randomness[J].Contemporary Sociology－A Journal of Reviews，2001，30（2）∶209－210.

[7]谢琼瑶，邓长虹，赵红生，等.基于有权网络模型的电力网节点重要度评估[J].电力系统自动化，2009，33（4）∶21－24.

[8]魏震波，刘俊勇，潘睿，等.基于P、Q网分解的有向加权拓扑模型下的电网脆弱性分析[J].电力系统保护与控制，2010，38（24）∶19－22.

[9]魏震波，刘俊勇，王佳佳.基于网络数字化挖掘的电网拓扑结构辨识[J].电力系统自动化，2011，35（4）∶12－17.

[10]倪向萍，梅生伟，张雪敏.基于复杂网络理论的输电线路脆弱度评估方法[J].电力系统自动化，2008，32（4）∶1－5.

[11]王凯.基于复杂网络理论的电网结构复杂性和脆弱性研究[D].武汉：华中科技大学，2011.

[12]王民昆，魏震波，刘俊勇，等.基于可靠性加权拓扑模型下的电网脆弱性评估模型[J].电工技术学报，2010，25（8）∶131－137.

[13]曹一家，陈晓刚，孙可.基于复杂网络理论的大型电力系统脆弱线路辨识[J].电力自动化设备，2006（12）∶1－5.

[14]LATORA V，M MARCHIORI.Efficient behavior of smallworld networks[J].Physical Review Letters，2001（87）∶15－19.

[15]丁明，韩平平.加权拓扑模型下的小世界电网脆弱性评估[J].中国电机工程学报，2008（10）∶20－25.

[16]史进，涂光瑜，罗毅.电力系统复杂网络特性分析与模型改进[J].中国电机工程学报，2008，28（25）∶93－98.

[17]王锡凡，徐林，王秀丽.使用等值导纳进行电力系统小世界特性识别[J].中国电机工程学报，2009，29（19）∶20－26.

[18]BOMPARD E，R NAPOLI，F XUE.Analysis of Structural Vulnerabilities in Power Transmission Grids[J].International Journal of Critical Infrastructure Protection，2009，2（1－2）∶5－12.

[19]ALBERT R，A L BARABASI.Statistical Mechanics of Complex Networks[J].Reviews of Modern Physics，2002，74（1）∶47－97.

[20]NEWMAN M.The Structure and Function of Complex Networks[J].Siam Review，2003，45（2）∶167－256.

[21]S BOCCALETTI，V TATORA，Y MORENDO，et al.Complex Networks∶Structure and dynamics[J].Physics Reports－review Section of Physics Letters，2006，424（4－5）∶175－308.