基于BP-PSO的SVC附加阻尼控制大电网试验

郑连清，曾治强，唐永红

(1.输配电装备及系统安全与新技术国家重点实验室(重庆大学)，重庆 400044；2.国网四川省电力公司 电力科学研究院，四川 成都 610031)

0　引言

随着电力系统的发展，电力系统的稳定性已成为人们关注的重要问题。为了提高电力系统阻尼，可以通过安装附加阻尼控制的静止型动态无功补偿装置SVC来实现，通过控制TCR中晶闸管的开通角度来改变并联电网电容容量大小，进而提供可调的感性无功功率[1]。附加阻尼控制器SVC的设计方法多种多样：文献[2]根据阻尼转矩概念提出了从理论上分析SVC阻尼调节和电压控制之间的相互作用关系。文献[3]将模糊逻辑控制智能算法和神经网络用于SVC附加阻尼控制器的设计，该算法过度依赖专家的经验和知识。文献[4]提出基于PSO的SVC附加阻尼控制器参数优化设计，但是只适用于小型电网络优化。文献[5]提出新型混合SVC模型及其基于人工免疫算法的控制策略，提高了系统稳定性，但并未进行大电网试验。文献[6]进行了实时仿真试验，但是并未提出具体的SVC阻尼控制器设计方法。

对于全网SVC附加阻尼控制器的设计，由于网络结构复杂，模型阶数过高，数学模型建立困难，导致传统优化算法的目标函数难以确定。本文提出BP-PSO算法，在优化过程中调用已经训练好的BP神经网络来代替无法确定的目标函数，达到优化目的。基于PSASP-ADPSS进行全网机电-电磁试验，验证该算法优化后参数的有效性。

1　SVC工作原理

SVC的结构有很多，本文采用TCR型SVC，稳态时投入80%固定电容器，暂态时通过控制晶闸管触发角来控制TCR输出等效导纳实现无功平滑补偿[7-8]。SVC的主要功能是电压无功调节，同时可以通过附加阻尼控制来增加系统阻尼，达到抑制电网低频振荡的目的。本文所用SVC动态调节和暂态控制的策略框见图1。

图1　SVC动态调节和暂态控制策略框图

SVC动态调节和暂态控制策略框图，主要由3部分组成：暂态强补控制、暂态电压控制和阻尼控制。其中暂态强补控制是在电网发生严重故障时投入的功能。为提高试验的可靠性，投入暂态强补控制能解决发生严重故障时物理装置对变电站500 kV电压锁相不准确的问题。SVC装置暂态强补以变电站500 kV电压作为判断条件，进入暂态强补控制的门槛为任意一相电压低于0.6 p.u.(以500 kV的相电压为基准)，投入暂态强补的时间为0.9 s。

电压控制输入为变电站500 kV相电压标幺值，采用传统PI控制。

阻尼控制环节采用尖山—九江500kV 线路功率波动之和DP作为输入信号，该控制环节包括1个隔直环节、2个超前滞后环节和1个比例环节，其传递函数为：

(1)

式中：Tw为隔直环节时间常数；T1～T4为两个超前滞后环节时间常数；KW为控制器增益。通过控制阻尼环节参数，使输入功率在特定的频段波动超前或者之后输出一定角度，即可以增加系统阻尼。阻尼环节输入、输出关系表达式为：

BPSDC=H(s)DP

(2)

式中：BPSDC为阻尼环输出等效导纳；H(s)为阻尼环传函；DP为阻尼环输入。

2　SVC阻尼环节的参数优化

2.1　BP神经网络

1986年Rumelhart，Hinton和Williams提出一种ANN的误差反向传播训练算法(简称BP算法)，它包含输入层、隐含层和输出层，是一种经典的多层前向型神经网络。含有一个隐含层的网络，可以拟合任何函数在理论上已经得到证明[9-10]。BP算法的运算过程是通过两个部分组成：正向传播过程给出每个单元实际输出值，该值通过输入信息和输入层与隐含层关系得到(第一阶段)；反向过程，若在输出值未达到理想状态时，逐次逆向计算期望输出与实际输出的差值(称为误差)，而后依据此值调整权值。具体运算即为计算每一权重的发送单元的激活值与接收单元的误差值之积。BP神经网络结构图的结构见图2。

图2　BP神经网络结构图

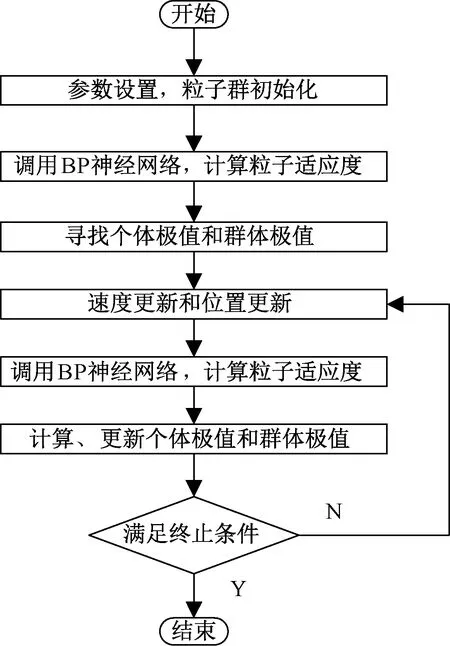
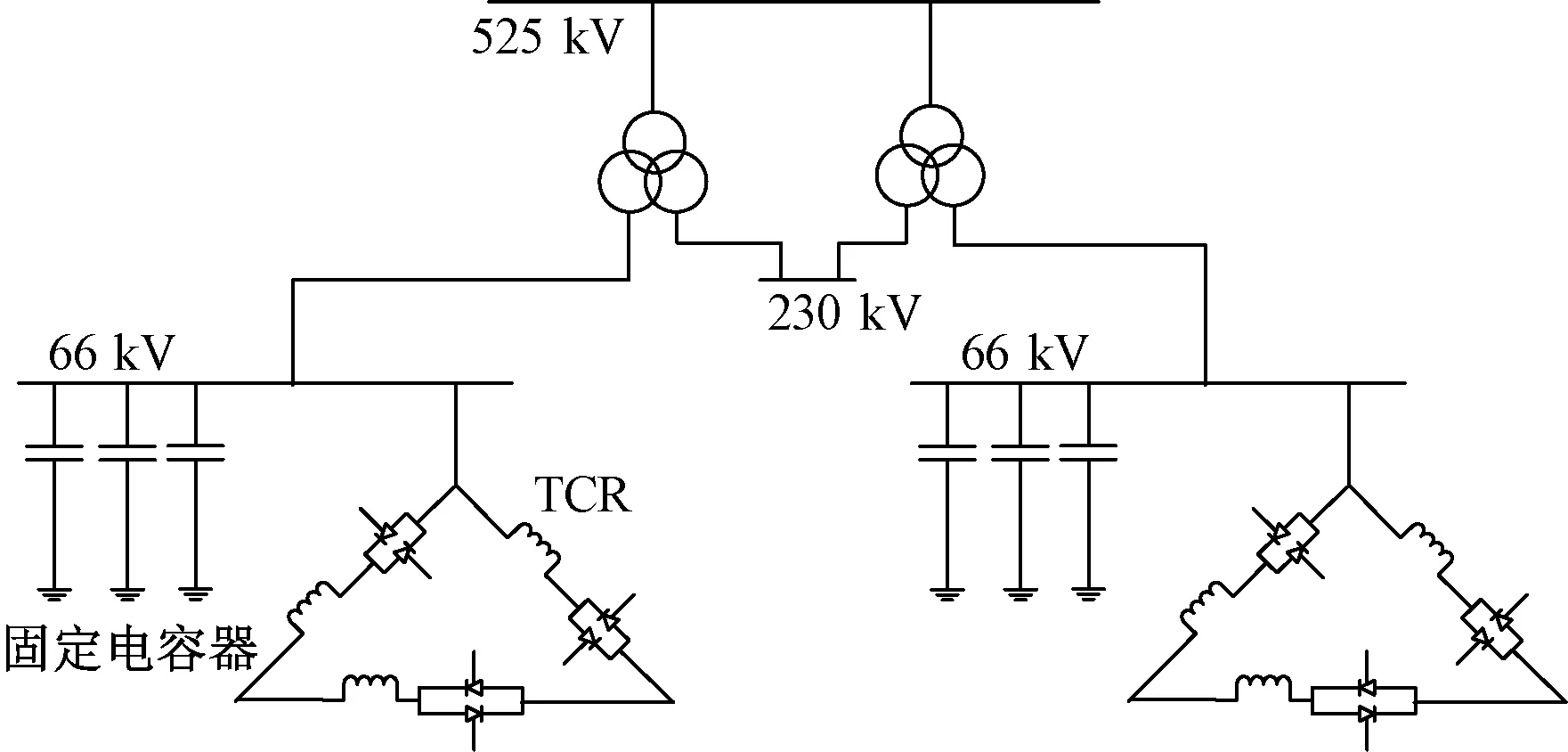
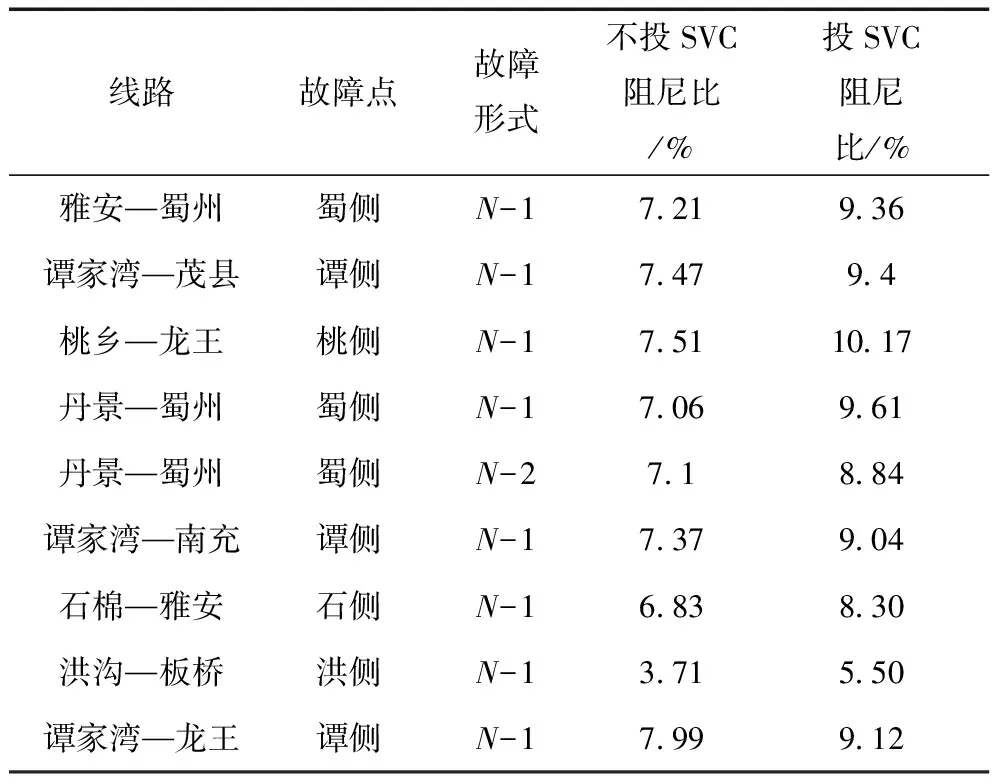
由于在线路近端、远端发生三相短路故障时，尖九有功波动频率大致为0.76 Hz，所以阻尼环隔直环节时间常数可取Tw=10 s、T2=3 s、T3=0.1 s，待优化参数为0

首先，根据所求目标函数和要优化的参数对BP神经网络进行训练。本文利用PSASP，基于同一潮流作业，对同一近端故障(雅安—蜀州N-1故障)进行暂态计算，得到尖九线路有功波动，通过PSASP曲线阅览室的Prony拟合，得到其阻尼比。KW=0(无阻尼控制)时，尖九线路有功波动Prony拟合如图3所示。

图3　Prony拟合分析

依据拟合结果得出，在无阻尼控制时，尖九有功波动阻尼比为7.211%。根据待优化参数取值范围，获取600组样本，其中500组作为训练样本训练BP神经网络，剩下100组作为测试样本。应用测试样本对训练好的BP神经网络进行准确性验证，BP神经网络的实际值和计算值如图4所示，可以看出，该网络能准确计算目标函数。

图4　BP神经网络训练结果

2.2　基于BP-PSO算法的参数优化设计

在BP-PSO算法中，所有粒子的行为都是作为群体行为而相互影响的：每个粒子的搜索趋势和行为都会被该种群中其他粒子的行为影响。在算法优化初期，需要对粒子群进行初始化，即在目标函数解空间的可行域中，随机产生一个粒子群[11-12]。所以这些通过初始化生成的粒子都是目标函数的可行解，并且由训练好的BP神经网络代替目标函数决定种群的适应度值。各个粒子将在可行解空间中运动，下一次粒子的行为(运动距离和运动方向)是取决于粒子这一次的搜索速度。在一次迭代结束后，由各个粒子统计出的群体极值pgd和个体极值pid对每个粒子的位置进行实时更新。

在BP-PSO算法中，每个粒子都是D维空间的一个点，其位置和速度都是D维空间的向量。例如，对于第i个粒子，它的位置表示为Xi=(xi0,xi1,xi2,…,xiDim)，i=1，2，…，N，其中N是粒子数目，Dim是粒子的维数。各个粒子逼近最优解的规则都是依据种群的群体极值pgd和自身的个体极值pid来选择决定其运动速度和方向。种群中不同粒子在运动过程的最优性是依据训练好的BP神经网络算出具体的个体适应度值决定的。下式给出进行优化迭代时，粒子的位置和速度更新公式：

vid(t+1)=wvid(t)+c1r1(pid-xid(t))

+c2r2(pgd-xid(t))

(3)

xid(t+1)=xid(t)+vid(t+1)

(4)

式中：r1、r2为[0，1]的随机数；w、c1和c2是分别为这3部分的权重系数。其中w称为惯性权重系数，c1和c2为粒子速度更新的加速因子。w的值越大搜索速度越慢但全局搜索能力强，进而难以达到最优值。上式可以看出粒子的速度公式包括以下3部分：(1)粒子上一时刻的搜索行为，即速度信息vi(t)，具有原先的速度信息；(2)自身的个体极值pid与当前位置的距离，该差值反映自身的搜索经验；(3)还涉及到了群体极值pgd来进行速度更新，该部分反映了各个粒子与整个群里的联系。为了使算法更加准确、快速，本文的w值依据文献[13]提出的线性递减惯性权重策略决定，在算法初期，有较大的w，后期逐渐递减，使寻优过程快速且不易陷入局部最优。w表达式如下：

式中：wstart为算法初始时的惯性权重；wend为当迭代次数达到最大值时的惯性权重，一般取wstart=0.9，wend=0.4；k为当前迭代代数；Tmax则为最大迭代次数[14～15]。

该算法的流程图见图5。

图5　BP-PSO算法流程图

种群规模为20，迭代代数为300。优化结果如下：T1=0.045 1、T3=0.029、KW=2.514 1。

利用MATLAB可以画出阻尼环节传函H(s)的伯德图见图6，可以看出在低频段0.7～2 Hz，阻尼环节输出之后输入一定角度。

图6　阻尼环的幅频和相频特性曲线

3　SVC投入大电网试验

3.1　SVC主电路参数

本试验基于全网模型作为电网系统的仿真模型。系统功率基准值为100 MVA，电压基准值为各母线的额定相电压。SVC装设在500 kV变电站低压侧(66 kV)，由1组180 MVar TCR、3组并联电容器组。见表1。

表1　SVC主电路参数表

SVC控制器有两种工作状态：自动状态和手动状态。处于自动状态时，SVC控制器投入动态调节和暂态强补功能，输出触发脉冲的角度由SVC控制器根据输入的电压功率信号进行动态调节。处于手动状态时，SVC控制器退出动态调节和暂态强补功能，输出触发脉冲的角度定为定角度调节角度(即定值所设定的角度值)，这种方式下TCR仅作为固定容量无功补偿设备。本文采用自动状态，稳态时投入3组60 Mvar电容器和TCR，TCR出力为80%，即输出等效导纳为144 Mvar。SVC控制器等值导纳输出范围标幺值为 -0.36～1.4 p.u.，无功出力为-144 Mvar(容性)～36 Mvar(感性)。

3.2　闭环试验系统

试验系统由PSASP-ADPSS共同完成，整个大电网在PSASP上进行建模，基于全网对整个系统进行自动子网划分，其中包括6个机电子网和1个电磁子网(500 kV变电站SVC部分)，电磁子网在ADPSS上搭建，并外接SVC实际控制器，通过并行计算和混合仿真方式实现全网的实时仿真。SVC接线示意图见图7，该图部分为电磁子网部分。

图7　SVC接线示意图

闭环试验系统组成见图8，ADPSS仿真装置通过物理接口(含功率放大器)向SVC控制器提供所需的电压、电流信号，同时接收SVC控制器发出的TCR各支路晶闸管的触发脉冲信号。SVC控制器从物理接口箱(含功率放大器)采集电压、电流信号，并通过物理接口箱(含功率放大器)输出触发脉冲信号至ADPSS仿真装置，从而在大电网仿真平台中实现对SVC控制器的闭环控制。

图8　闭环试验系统组成

3.3　SVC投入大电网试验

把由BP-PSO算法优化后的SVC控制参数代入SVC阻尼控制环节，对装设SVC的变电站近端、远端相关线路故障进行三相短路故障，分析SVC装置的动态无功调节和暂态强补功能对系统阻尼的影响。几种故障后尖九500 kV线路有功功率的阻尼比对比情况见表2。故障开始时间为5 s，并在0.1 s后切除故障。

表2　投与不投SVC阻尼比对比表

再次扫描近端、远端故障后，SVC控制器不投入和投入两种情况下二滩#1机组相对于三峡左#1机组功角振荡曲线的对比图、尖九有功波动图见图9 (a)～(c)。

图9　尖九有功(左)、二滩—三峡功角(右)

在雅安—蜀州N-1故障下，变电站500 kV母线电压、TCR无功出力波动图见图10，从下图可以看出，故障在5 s时开始，并在0.1 s后切除，在故障开始的0.9 s内，TCR电感全切，完全释放TCR无功出力，之后推出暂态强补，进步电压—阻尼环控制，动态调节TCR出力。

图10　雅蜀N-1，变电站500kV电压、TCR出力

结合上表的分析和各种故障方式下的二滩—三峡的功角图看出，投入SVC阻尼控制器后，通过SVC的暂态强补和阻尼控制功能有助于提高二滩机组相对于三峡机组间功角振荡的阻尼比。类似地，江边—三峡等机组的功角差、尖九有功功率的振荡阻尼比也较未投入SVC控制器时有所提高，均无阻尼比下降的情况。因此，经BP-PSO算法优化后的九江SVC装置具有提高系统阻尼的作用。

4　结论

(1)本文提出了BP-PSO算法用于SVC阻尼环节参数优化，利用训练好的BP神经网络代替目标函数求解PSO适应度，解决对于建模困难、目标函数难以确定的大电网的SVC参数优化。

(2)基于PSASP-ADPSS搭建SVC闭环试验系统，对大电网进行投入SVC试验，试验表明：BP-PSO算法优化之后的SVC阻尼控制器投入大电网与未投入SVC在各种故障下比较，尖九线路有功功率阻尼比大致可以提高2%～3%，该算法优化下的SVC可以很好地抑制大电网系统低频振荡，提高系统的暂态稳定性。

参考文献：

[1]付伟,刘天琪,李兴源,等.静止无功补偿器运行特性分析和控制方法综述[J].电力系统保护与控制,2014,42(22):147-154.

[2]刘隽,李兴源,汤广福.SVC电压控制与阻尼调节间的相互作用机理[J].中国电机工程学报,2008,28(1):12-17.

[3]KUMKRATUG P.Static var compensator based on fuzzy logic control for damping power system oscillation[J].American Journal of Applied Sciences,2011,8(10):1027-1031.

[4]吕锋,张健.基于PSO的SVC附加阻尼控制器参数优化设计[J].电力电容器与无功补偿,2016,37(2):11-15.

[5]陈赛赛,李可军,王卓迪,等.新型混合SVC模型及其基于人工免疫算法的控制策略[J].电力自动化设备,2016,36(4):93-99.

[6]胡涛,刘翀,班连庚,等.藏中电网SVC控制策略实时仿真及参数优化[J].电网技术,2014,38(4):1001-1007.

[7]朱金奇.TCR+FC型SVC原理及应用[J].电气传动自动化,2006,29(5):114-116.

[8]粟时平,左鹏辉,刘桂英.基于滚动投切型SVC的智能控制器的研究[J].电力科学与工程,2014(5):28-33.

[9]XIE R,WANG X,LI Y.Research and application on improved BP neural network algorithm[C]//Industrial Electronics and Applications.IEEE,2010:1462-1466.

[10]袁圃,毛剑琳,向凤红,等.改进的基于遗传优化BP神经网络的电网故障诊断[J].电力系统及其自动化学报,2017,29(1):118-122.

[11]李炳宇,萧蕴诗,汪镭.PSO算法在工程优化问题中的应用[J].计算机工程与应用,2004,40(18):74-76.

[12]郁磊.MATLAB智能算法30个案例分析[M].北京: 北京航空航天大学出版社,2015.

[13]EBERHART R C,SHI Y.Comparing inertia weights and constriction factors in particle swarm optimization[C].Evolutionary Computation,2000.Proceedings of the 2000 Congress on.IEEE Xplore,2000:84-88.

[14]马立新,王继银,项庆,等.三目标混合骨干粒子群算法的电力系统无功优化[J].电力科学与工程,2015(11):18-23.

[15]王东风,孟丽.粒子群优化算法的性能分析和参数选择[J].自动化学报,2016,42(10):1552-1561.