移动卫星通信系统强跟踪姿态估计算法研究

2018-04-18关钦锦

数字通信世界 2018年1期

关键词：时变增益滤波器

关钦锦

（南京六九零二科技有限公司，南京 210000）

1 强跟踪滤波算法

在强跟踪滤波算法中，进行滤波估计，要不断的调整时变增益阵Kk，根据正交性原理，可以得到最小均方误差阵，而且此时一定是处处正交[1]。

正交性原则：

在上式中，xk是在k时刻时，被估计的状态矢量，最小值为min，在k时刻的残差表示为εk。

因为没有确定模型，所以，一旦滤波器的状态估计值脱离了轨迹，残差就会表现出来。为了满足滤波的增益，会强迫强跟踪波跟踪真实的状态。

强跟踪波的系统模型：

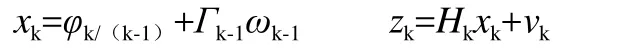
此时K和j的值取1，2到正无穷。

在上式中，φk/（k-1）代表的是状态量在（k-1）～k 的转移矩阵；k时刻的观测矩阵表示为Hk，k时刻的观测值为zk；在k-1到k时刻，系统噪声的观测值表示为Γk-1；ωk-1和vk-1都是零均值的高斯白噪声。

强跟踪滤波器

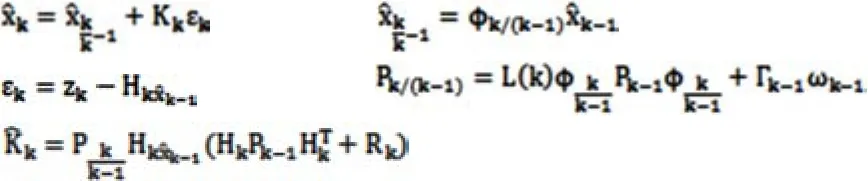
上式中，Lk代表着时变渐消因子矩阵，并且

Lk=diag（λ1（k），λ2（k），，λn（k））

其中，λ1（k）表示的是时变渐消因子，并且

λ0=tr（N（k+1））/tr（M（k+1））

在上式中，时变系数比例是γ，在先验信息中可以得到，tr表示矩阵的迹。

在k时刻，滤波的协方差矩阵表示如下：

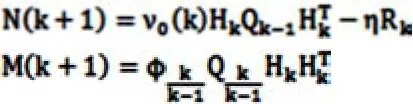
在上式中，0≤ρ≤1代表遗忘因子。在正常的情况下，ρ的取值为0.95；η≥1表示弱化因子，当取η的值为2时，状态值的估计结果更加的平滑。

2 渐消因子的推导以及计算

在强跟踪滤波中，引入一些渐消因子，实现调整一步预测方差阵。但是与此同时，也破坏了预测误差方差阵的对称性，因此可以引入镜像时变因子矩阵L（k）T，这样可以保证对称性。经过改进以后，预测协方差矩阵如下：

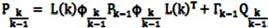
在初始算法中，计算时变因子时，需要用到先前的信息，导致初始算法存在不稳定性。所以，为了保证稳定性，将新时变因子的计算方法引入。

因为正交性原理是，所以我们可以推算出其充要条件是：

之后，将Kk表示的滤波增益引入后得到：

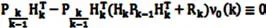
将上式进行简化，得到

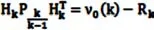
然后，引入Pk/（k-1）可以得到下式：

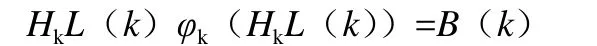
将上式中的 HkL（k）令成（λ1（k）h1，λ2（k）h2，，λn（k）hn），Hk=（h1，h2，，hn），然后代到上式中，并且整理一下，就可以得到：

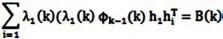
在这里，我们选用了迭代法。

将初始值λ（0）=（1，1，1，，1），从而得到了如下的迭代式：

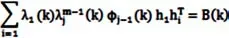
在上式中，迭代次数为m。

最终的时变因子结果如下：

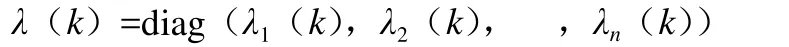
当 λi（m）≥1时，λ1=λi（m）；当 λi（m）小于1的时候，λ1的值为1。

3 仿真结果

结合强跟踪滤波器的特点，预处理实验数据，选择动态特性比较强的一些部分，可以更好的表现问题，在强机动和高动态的情况下，强跟踪滤波有较好的数据滤波结果。载体有较强的动态特性，并且真实的数据和量测的数据之间还有较大的误差。可以看出，载体在10s、35s以及50s出表现出了明显的跳变。将强跟踪滤波（STF）和扩展卡尔曼滤波器（EKF）的仿真数据的滤波结果进行分析对比，可以看出，两者都可以稳定跟踪载体动态，下图2是两者的对比。在突变节点，强跟踪滤波表现出更强的滤波效果。