SAR图像相干斑的非局部平均滤波算法
2018-04-18朱磊蔡飞飞王延年郭林源
朱磊, 蔡飞飞, 王延年, 郭林源
(西安工程大学电子信息学院, 710048, 西安)
SAR图像中大量随机散布着一种被称为相干斑的固有乘性噪声。相干斑的存在不仅严重影响了SAR图像的视觉质量,而且对SAR图像后续解译处理技术的有效性与可靠性也造成了明显干扰[1-2],因此,相干斑抑制算法研究一直是SAR图像处理研究领域的一项重要内容。
SAR图像抑斑算法可大致分为3类:空域滤波[3-5]、偏微分各向异性扩散滤波[6-8]及变换域滤波[9-11]。空域滤波出现最早,以经典LEE滤波[3]及其改进算法[4-5]等为代表。该类算法利用滑动窗口估计的局部统计量,自适应地控制对相干斑的平滑滤波,具有算法相对简单、实时性好等优点,但这类算法普遍存在抑斑性能受局域窗尺度选择影响大且噪声抑制不充分等问题。以经典各向异性(SRAD)扩散滤波[6]及其改进算法[7-8]等为代表的各向异性扩散滤波,可视为一种迭代运行的特殊空域滤波。该类算法大多利用滑动窗口估计的局部统计量来自适应控制扩散滤波的方向与强度,能在相干斑抑制与边缘细节保护上实现较好的平衡,同时也便于在扩散滤波中融入增强、腐蚀等其他处理。然而,这类算法往往至少需要经过数十次迭代运算,存在计算量较大,迭代运算次数难以准确预判及图像动态范围收缩明显等问题。近年来,具有多尺度分解、稀疏表示等优势的小波变换、轮廓波变换、二维S变换等采用阈值收缩的变换域抑斑算法[9-11],在相干斑抑制与细节保持方面展现了较为优异的性能,然而这类算法容易在抑斑图像中产生伪吉布斯条纹。大部分空域滤波或各向异性扩散滤波均属于局部加权平均,存在局域窗尺度过大容易导致图像细节损失,而窗尺度过小则易导致抑斑不彻底等问题。2005年,Buades等针对图像加性噪声抑制问题,提出了著名的非局部平均(NLM)滤波[12],从而为提升图像噪声抑制性能提供了一种新思路,而Sara、Chen、Deledalle等先后从变换域、空域等不同角度,将NLM思想应用于SAR图像乘性相干斑抑制领域并取得了令人鼓舞的抑斑效果[13-15]。
为此,本文尝试利用NLM滤波思想来提升SAR图像的抑斑性能,提出了一种以均值比与变差系数联合构建的NLM滤波算法(MR-NLM)。该算法主要有以下改进:①首次提出利用对乘性相干斑噪声具有恒虚警边缘检测性能的均值比,替代传统NLM滤波中的高斯加权欧氏距离来构建相似性测量参量,从而使得NLM滤波对SAR图像不同灰度值区域均具有程度相似的边缘保持能力与相干斑抑制水平;②利用能较好检测SAR图像同质区与边缘区的变差系数,替代传统NLM滤波中的常系数来构建衰减因子,从而使得NLM滤波能自适应控制在同质区和边缘区的平滑强度,确保在抑斑的同时,进一步保护边缘。实验结果表明,本文算法能有效提升SAR图像相干斑抑制与边缘保护性能。
1 经典NLM滤波
经典NLM滤波[12]在对加性噪声图像滤波时,通过估计非局部的大尺度搜索窗内每个像素与中心像素在小尺度相似窗下的高斯加权欧氏距离,来测量搜索窗内每个像素与中心像素之间的相似性程度,并以此作为确定每个像素加权系数大小的主要参量。
设位置i处观测值为X(i),有用信号为S(i),则噪声为N(i)的加性噪声图像模型为
X(i)=S(i)+N(i)
(1)
那么,经典NLM滤波算法对图像i位置像素进行非局部加权平均滤波,可描述为
(2)
式中:Ω(i)表示以i为中心的大尺度搜索窗;w(i,j)表示搜索窗内j像素对i像素的加权系数。加权系数w(i,j)的计算可表示为
(3)
式中:h为控制负指数衰减速度的衰减常数;B(i)为正则化因子,可表示为
(4)
其中DGWED(i,j)表示在搜索窗Ω(i)内i像素与j像素之间的高斯加权欧氏距离,可表示为
(5)
其中,ψ(i)与ψ(j)分别表示以i、j为中心的小尺度相似窗,Y(ψ(i))与Y(ψ(j))分别表示在相似窗ψ(i)与ψ(j)处的图像观测值矩阵,‖‖2,σ表示计算标准差为σ的高斯加权2-范数。
经典NLM算法由于采用了非局部的大尺度搜索窗来实施加权滤波,从而让更多的有效像素可以参与到滤波参数估计与噪声平滑处理中,使得提升噪声抑制与边缘保护性能成为了可能,而将高斯加权欧氏距离DGWED作为相似性测量参量,则让经典NLM滤波算法与传统局部平均算法不同,不会因加权窗尺度过大而导致滤波图像模糊。正是因为经典NLM滤波的上述优势,文献[14]将NLM滤波思想及DGWED应用到SAR图像相干斑抑制中并取得了不错的抑斑效果。然而,直接将DGWED应用到SAR图像中,会由于相干斑的乘性噪声属性,导致滤波算法抑斑强度在不同灰度值同质区大小差异明显,同时,也容易引起不同区域边缘检测的非恒虚警等问题。为此,本文提出利用对SAR图像乘性相干斑具有恒虚警边缘检测性能的均值比,替代DGWED构建相似性测量参量,并在下文分析了采用均值比与DGWED作为相似性测量参量的差异。
2 利用均值比与变差系数的NLM滤波新算法
本文提出了一种利用均值比与变差系数联合构建的NLM滤波算法(MR-NLM),该算法需先利用均值比估计相似性测量参量,再利用变差系数估计自适应衰减因子,然后利用相似性测量参量与自适应衰减因子联合估计负指数加权系数,最后对SAR图像实施非局部加权滤波,算法流程如图1所示。
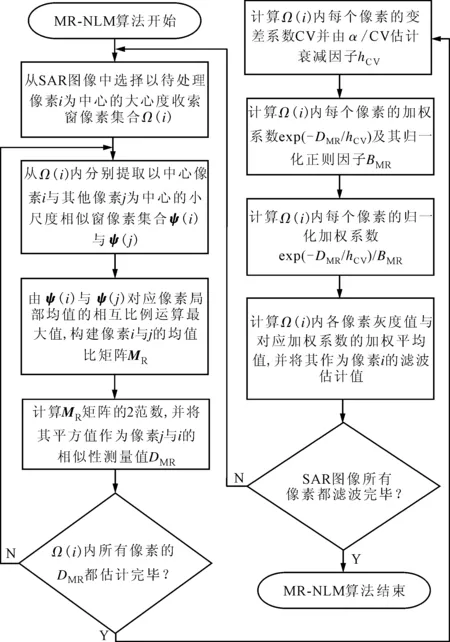
图1 本文MR-NLM算法流程图
2.1 利用均值比构建相似性测量参量
设位置i处观测值为X(i),回波信号为S(i),相干斑为N(i)的SAR图像乘性模型为
X(i)=S(i)N(i)
(6)
由式(6)易知,信号S(i)的值越大,则相干斑N(i)引起观测值X(i)偏离信号S(i)的程度也越剧烈。文献[16]已证明,与应用于加性噪声图像模型的梯度等差分运算不同,比率运算可实现对SAR图像乘性相干斑模型的恒虚警边缘检测。为此,本文提出利用均值比来构建相似性测量参量,从而使得NLM滤波对SAR图像不同灰度值区域均具有相似程度的相干斑抑制性能。
利用均值比构建的相似性测量参量可描述为
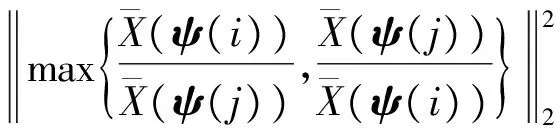
(7)
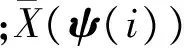
(8)

(a)5视真实SAR图像 (b)8视真实SAR图像

(c)A窗DMR矩阵 (d)B窗DMR矩阵 (e)A窗DGWED矩阵

(f)B窗DGWED矩阵 (g)E窗DMR矩阵 (h)F窗DMR矩阵

(i)E窗DGWED矩阵 (j)F窗DGWED矩阵图2 利用DMR与DGWED构建的相似性测量矩阵图像对比
图2以一个简单实例显示了DMR与DGWED分别作为相似性测量参量所表现出的差异。在图2a、2b两幅真实SAR图像中,分别在边缘与同质区选取A、B、E、F4处区域,然后利用DMR与DGWED计算各窗对应的相似性测量矩阵,并将相似性测量矩阵以图像形式展示在图2c~2j中。
根据相似性测量的要求,搜索窗内的像素与中心像素的相似程度越高,则其被分配的相似性测量值越小(因采用负指数衰减加权)。图2中,A与B窗的中心像素均刚好位于边缘上,因此,A与B窗内仅边缘附近像素与中心像素相似度高。由图2c~2f可见,利用DMR获得的测量矩阵图像,其边缘附近测量值明显低于两侧同质区且测量值比较平滑,展现了较好的边缘与同质区区分度,而利用DGWED获得的测量矩阵图像,虽也能区分边缘与同质区,但边缘两侧同质区测量值起伏较大,同质区部分像素测量值甚至与边缘区像素相近。因此,DMR能对A与B窗形成更好的相似性测量,这将使得采用DMR的本文算法能更好的保护边缘。由图2g与2h可见,高灰度值同质区的E窗与低灰度值同质区的F窗像素分配的DMR测量值差异小。由图2i与2j可见,高灰度值的E窗分配的DGWED测量值平均水平要明显高于低灰度值的F窗,这将导致采用DGWED的NLM滤波算法,在低灰度值区域的抑斑能力较强,而高灰度值区域较弱,造成不同区域相干斑抑制程度差异明显,而采用DMR的本文算法则可确保各区域之间具有相近的抑斑强度。
2.2 利用变差系数构建自适应衰减因子
传统NLM滤波算法在对图像平滑去噪时,采用单一常数作为衰减因子,显然存在弊端。当衰减因子取值较小时,NLM滤波算法对边缘细节保护较好,但噪声残留较多;当衰减因子取值较大时,噪声抑制较彻底,但容易导致边缘模糊。因此,只有NLM滤波算法对SAR图像同质区与边缘区域采用不同的衰减因子,方能兼顾相干斑抑制与边缘保护。
变差系数是一种能较好评估SAR图像局部起伏程度的参量,考虑到SAR图像大部分边缘引起的起伏一般较同质区相干斑引起的起伏更剧烈,因此,变差系数常被抑斑算法[3-4,6-8]用作检测边缘区与同质区的有效参量,其检测准确度随相干斑强度减弱而提高。变差系数的定义为
(9)
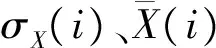

图3 图2a真实SAR图像的VCV矩阵图像
图3表明,VCV值在边缘区域偏高而同质区偏低,可见VCV对SAR图像不同区域具有较好的检测与区分能力。为此,本文提出利用VCV代替传统NLM滤波算法中的常数衰减因子,在NLM滤波中形成一种随SAR图像区域变化而自适应变化的衰减因子。同时,考虑到衰减因子在同质区应取较大值,以加大NLM滤波算法对同质区相干斑的抑制强度;而在边缘区域应取较小值,以减弱对边缘的过度平滑,因此本文提出的由VCV估计的自适应衰减因子定义为
(10)
式中:α为整体调节算法抑斑强度的衰减常数。
2.3 基于NLM滤波的非局部加权平均滤波
由式(7)构建的相似性测量参量与式(10)构建的自适应衰减因子,容易得出本文MR-NLM算法的加权系数为
(11)
式中:BMR(i)为正则化因子,可表示为
(12)
本文算法的非局部加权滤波运算可表示为
(13)
为验证本文MR-NLM算法的加权系数对边缘的有效保护,图4比较了MR-NLM算法与NL-CV算法[14]对图2a真实SAR图像边缘区域A与B窗的加权系数矩阵图像。显然,与NL-CV算法相比,本文MR-NLM算法仅对边缘附近像素分配了较大权值,而对边缘两侧同质区分配的权值较小且更均匀、起伏更小,因此,MR-NLM算法加权系数更有利于保护边缘。

(a)A窗NL-CV系数矩阵 (b)B窗NL-CV系数矩阵

(c)A窗MR-NLM系数矩阵 (d)B窗MR-NLM系数矩阵图4 图2a中A与B窗的NL-CV与MR-NLM系数矩阵图像
3 实验与结果
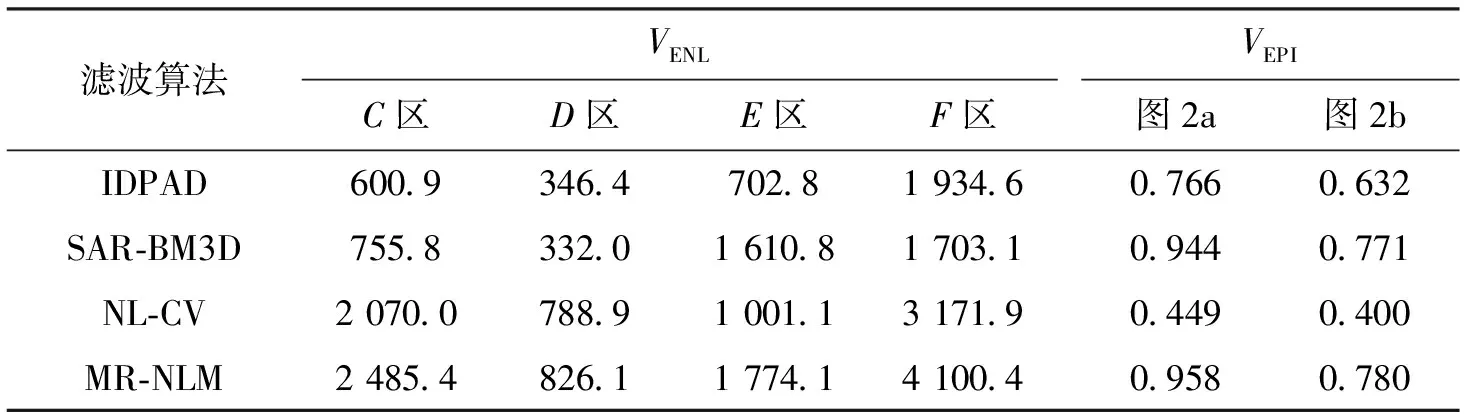
为了检验滤波算法的抑斑性能,分别采用本文MR-NLM算法、各向异性扩散IDPAD算法[7]、变换域SAR-BM3D算法[13]及空域NLM滤波算法(NL-CV)[14],对图2a与2b两幅真实SAR图像进行抑斑处理,并对抑斑性能进行视觉效果评估与参数性能比较,视觉效果比较包括抑斑图像的视觉效果比较以及抑斑图像的Canny边缘检测图像比较,实验结果如图5与图6所示。参数性能比较采用了文献[4]中使用的两个参数:等效视数VENL与边缘保持指数VEPI。VENL常用于评估抑斑能力强弱,其值越大说明抑斑算法的相干斑抑制能力越强;VEPI常用于评估边缘保持能力强弱,其值越接近于1表明抑斑算法的边缘保持性能越强。实验中VENL参数评估区域选择了图2a中的C区与D区以及图2b中的E区与F区,实验结果如表1所示。
为了客观体现各算法相干斑抑制与边缘保护的最好性能,各算法在对图2a与2b两幅SAR图像抑斑时,分别采用了各自最好的抑斑性能参数。各算法对图2a抑斑时采用的参数为:SAR-BM3D算法的视数L设置为5;IDPAD算法的局域窗尺度为5
×5像素,时间步长为0.05,迭代运算20次;NL-CV算法搜索窗尺度为21×21像素,相似窗尺度为7×7像素,衰减常数为85,高斯核标准差为8;本文

(a)SAR-BM3D算法

(b)IDPAD算法

(c)NL-CV算法

(d)MR-NLM算法图5 4种算法对图2a、2b两幅真实SAR图像的抑斑效果对比
滤波算法VENLC区D区E区F区VEPI图2a图2bIDPAD6009346470281934607660632SAR⁃BM3D75583320161081703109440771NL⁃CV207007889100113171904490400MR⁃NLM248548261177414100409580780

(a)图5a对应的边缘检测图像

(b)图5b对应的边缘检测图像

(c)图5c对应的边缘检测图像

(d)图5d对应的边缘检测图像图6 4种算法的抑斑图像对应的边缘检测图像对比
算法搜索窗尺度为21×21像素,相似窗尺度为7×7像素,衰减常数α为1.5;Canny算子的边缘检测阈值为0.08。各算法对图2b抑斑时采用的与图2a不同的参数为:SAR-BM3D算法的L为8;IDPAD算法迭代运算30次;NL-CV算法衰减常数为50;本文算法衰减常数α为3.6。
从图5所示的各算法抑斑图像对比可以发现:本文MR-NLM算法抑斑图像自然清晰,同质区相干斑抑制彻底,边缘保持充分,不存在SAR-BM3D算法抑斑图像中的伪吉布斯条纹,不存在IDPAD算法抑斑图像同质区中散布的块状起伏,不存在NL-CV算法抑斑图像高灰度值与低灰度值区域的明显差异。从图6所示的抑斑图像边缘检测图像对比可以发现:SAR-BM3D、IDPAD与NL-CV算法的边缘检测图像在高灰度值区域虚假边缘较多,本文算法边缘检测图像边缘平滑度更好,高灰度值区域虚假边缘更少。
由表1所示的抑斑性能参数比较容易发现:在表征相干斑抑制能力的VENL参数方面,本文MR-NLM算法在C~F4个同质区都展现了较其他3种算法更明显的优势,而这一结论与图5中本文算法抑斑图像所展示的更平滑的同质区,以及与图6中本文算法同质区边缘检测图像虚假边缘残留最少结果一致;在表征边缘保持性能的VEPI参数方面,本文MR-NLM算法略优于边缘保持性能优异的SAR-BM3D算法,但明显优于IDPAD与NL-CV算法,而这一结论与图5中本文算法抑斑图像所保留的更清晰的边缘,以及与图6中本文算法边缘检测图像边缘保持更完整结果一致。
4 结 论
本文将NLM滤波思路应用于SAR图像乘性相干斑噪声的抑制中,提出了一种以均值比与变差系数联合构建的NLM滤波新算法。该算法首次提出利用对乘性相干斑噪声具有恒虚警检测性能的局部均值比来构建NLM滤波的相似性测量参量,从而改良了传统相似性测量参量对边缘检测非恒虚警以及对不同灰度值同质区域相干斑抑制程度不均衡问题。同时,利用对SAR图像同质区与边缘区具有较好检测性能的变差系数来构建自适应的衰减因子,从而在抑斑的同时,进一步保护图像边缘。上述改进使得本文算法在抑斑图像视觉效果、相干斑抑制及边缘保护方面均优于多种传统算法。
参考文献:
[1]FELIX B, GERALDINE Q, THIMM Z, et al. Comparative analysis of edge detection techniques for SAR images [J]. European Journal of Remote Sensing, 2016, 49(1): 205-224.
[2]MORANDEIRA N S, GRIMSON R, KANDUS P. Assessment of SAR speckle filters in the context of object-based image analysis [J]. Remote Sensing Letters, 2016, 7(2): 150-159.
[3]LEE J S. Digital image enhancement and noise filtering by using local statistics [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1980, 2(2): 165-168.
[4]朱磊, 水鹏朗, 章为川, 等. 利用区域划分的合成孔径雷达图像相干斑抑制算法 [J]. 西安交通大学学报, 2012, 46(10): 83-88.
ZHU Lei, SHUI Penglang, ZHANG Weichuan, et al. A despeckling algorithm for synthetic aperture radar image using region subdivision [J]. Journal of Xi’an Jiaotong University, 2012, 46(10): 83-88.
[5]杨学志, 叶铭, 吴克伟, 等. 结构保持的双边滤波极化SAR图像降噪 [J]. 电子与信息学报, 2015, 37(2): 268-275.
YANG Xuezhi, YE Ming, WU Kewei, et al. A despeckling algorithm for synthetic aperture radar image using region subdivision [J]. Journal of Electronics & Information Technology, 2015, 37(2): 268-275.
[6]YU Y, ACTON S. Speckle reducing anisotropic diffusion [J]. IEEE Transactions on Image Processing, 2002, 11(11): 1260-1270.
[7]ZHU Lei, ZHAO Xiaotian, GU Meihua. SAR image despeckling using improved detail-preserving anisotropic diffusion [J]. Electronics Letters, 2014, 50(15): 1092-1093.
[8]朱磊, 韩天琪, 水鹏朗, 等. 一种抑制合成孔径雷达图像相干斑的各向异性扩散滤波方 [J]. 物理学报, 2014, 63(17): 445-455.
ZHU Lei, HAN Tianqi, SHUI Penglang, et al. An anisotropic diffusion filtering method for speckle reduction of synthetic aperture radar images [J]. Acta Physica Sinica, 2014, 63(17): 445-455.
[9]BHUIYANR M, AHMAD M, SWAMY M. Spatially adaptive wavelet-based method using the Cauchy prior for denoising the SAR images [J]. IEEE Transactions on Circuits and Systems for Video Technology, 2007, 17(4): 500-507.
[10] XU Bin, CUI Yi, LI Zenghui, et al. Patch ordering based SAR image despeckling via transform-domain filtering [J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2015, 8(4): 1682-1695.
[11] GAO Fei, XUE Xiangshang, SUN Jinping, et al. A SAR image despeckling method based on two-dimensional S transform shrinkage [J]. IEEE Transactions on Geoscience & Remote Sensing, 2016, 54(5): 3025-3034.
[12] BUADES A, COLL B, MOREL J M. A non-local algorithm for image denoising [C]∥Proceedings of
IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Piscataway, NJ, USA: IEEE, 2005: 60-65.
[13] SARA P, MARIANA P, CESARIO V A, et al. A nonlocal SAR image denoising algorithm based on LLMMSE wavelet shrinkage [J]. IEEE Transactions on Geoscience & Remote Sensing, 2012, 50(2): 606-616.
[14] CHEN Shaobo, HOU Jianhua, ZHANG Hua, et al. De-speckling method based on non-local means and coefficient variation of SAR image [J]. Electronics Letters, 2014, 50(18): 1314-1316.
[15] DELEDALLE C A, DENIS L, TUPIN F, et al. NL-SAR: A unified nonlocal framework for resolution preserving (pol)(in) SAR denoising [J]. IEEE Transactions on Geoscience & Remote Sensing, 2015, 53(4): 2021-2038.
[16] TOUZI R, LOPES A, BOUSQUET P. A statistical and geometrical edge detector for SAR images [J]. IEEE Transactions on Geoscience & Remote Sensing, 1988, 26(6): 764-773.
[本刊相关文献链接]
张欣,黄普明,文珺,等.一种适用于中高轨合成孔径雷达卫星的分辨率分析方法.2016,50(8):70-76.[doi:10.7652/xjtuxb201608012]
陈倩倩,张磊,徐刚,等.利用多通道联合稀疏重建的干涉逆合成孔径雷达三维成像算法.2014,48(12):100-106.[doi:10.7652/xjtuxb201412016]
董祺,张磊,徐刚,等.采用子孔径分割的逆合成孔径雷达成像包络对齐方法.2014,48(12):107-112.[doi:10.7652/xjtuxb201412017]
孟自强,李亚超,李浩林,等.双/多基地合成孔径雷达前视三维分辨力研究及运动参数设计.2014,48(8):29-35.[doi:10.7652/xjtuxb201408006]
杨桃丽,索志勇,李真芳,等.地球同步轨道合成孔径雷达干涉测量模型.2014,48(4):85-89.[doi:10.7652/xjtuxb 201404015]
侯兴松,张兰,肖琳.合成孔径雷达图像的贝叶斯压缩感知重构算法.2013,47(8):74-79.[doi:10.7652/xjtuxb201308013]
朱磊,水鹏朗,章为川,等.利用区域划分的合成孔径雷达图像相干斑抑制算法.2012,46(10):83-88.[doi:10.7652/xjtuxb201210015]
陈士超,武其松,吴玉峰,等.一种大斜视双基地合成孔径雷达的频率变标成像算法.2011,45(10):82-87.[doi:10.7652/xjtuxb201110015]
