耐用度服从三参数Weibull分布的机床刀具在变加工条件下的可靠性评估

王智明, 任丽娜, 段红燕, 杨海鱼

(兰州理工大学机电工程学院, 730050, 兰州)

金属切削刀具作为机床的重要组成部分,其可靠性对整个机床工艺系统的加工效率和稳定性有显著的影响。量化评估刀具的可靠性,及时更换不合格刀具[1-3],不仅可以降低生产成本,提高经济效益,而且还可以保证工件表面加工质量,因此准确评估刀具的可靠性具有重要的经济价值。

刀具寿命是刀具可靠性评估的主要指标之一,主要影响因素有切削速度v、进给量f、切削深度a等切削用量,因此以切削用量为主要模型参数的Taylor刀具寿命指数方程多元线性回归法为常见的刀具寿命评估方法之一[4-5]。但是,影响刀具寿命的因素众多,除切削用量外,还有刀具几何形状、刀具材料、工件材料、切削液及操作者的经验水平等。

概率统计法常用来评估刀具寿命及其可靠性。该方法认为刀具寿命为随机变量,且当刀具磨损形式为月牙洼磨损时,其寿命服从正态分布或对数正态分布;当磨损形式为刀面附着磨损时,寿命服从Gamma分布;大多数情况下,刀具寿命服从Weibull分布。其中,Iakovou等解决了刀具寿命为Gamma分布时的加工经济问题[6],Kwon等研究了金属陶瓷刀具寿命正态分布时的切削特性[7],Galante等给出了刀具寿命逆正态分布下的Taloy公式近似解法[8],樊宁等分析了刀具寿命服从对数正态分布时的可靠性[9],陈保家等提出了一种基于Logistic回归模型和刀具振动信号的可靠性评估方法[10],Letot等根据车削恶化指标预测了刀具的剩余寿命及可靠性[11]。

单一的统计分布模型未考虑切削用量等物理因素对刀具使用寿命及可靠性的影响,文献[12-13]综合统计分布模型和切削用量等可靠性主要影响因素,应用刀具寿命统计分布比例危险模型分析了刀具的可靠性。比例危险模型是Cox在1972年提出的生存数据分析的主要模型,认为对生存数据的建模需要考虑个体的异质性影响,因该模型在Weibull等统计分布模型的基础上综合了影响个体差异的协变量,后来被推广应用于可靠性分析领域[14]。李常有等分析了刀具在恒定加工及定期补偿条件下的刀具渐变状态可靠性[15-16]。然而,在机械加工中,为了满足工件不同的粗、精加工和表面质量等加工工艺要求,同一把刀具除切削用量不断变化外,加工部位及零部件类型亦不断变化[17-21]。如45°外圆车刀,不仅能车削轴类零件外圆面,也可以车削盘类零件端面或倒角。可见,由于刀具加工条件的变化,不能直接用不同加工条件下的工作时间进行可靠性分析,因此如何评价切削刀具在变加工条件下的可靠性便成为一个难题。

两参数Weibull分布可靠性模型可用常见的最小二乘法和极大似然法进行求解,且当其形状参数为1时,退化为更为简单的指数分布模型。因此,两参数Weibull分布模型具有参数估计简单和灵活性较强的特点,在可靠性分析中被广泛应用。当用该模型分析刀具的可靠性时,表示刀具在任意时间内均有可能发生故障。然而,根据工程实践经验可知,许多刀具在投入使用后的某一时间段内是不会发生故障的,且故障数据经双对数变换后在概率图上不是一条直线,此时用三参数Weibull分布模型分析刀具故障更为合适。这是由于三参数Weibull分布模型因位置参数的存在,可用来描述刀具在某一使用时间段内不发生故障的情况,且变换后的故障数据不在一条直线上[22-23]。

本文综合考虑切削用量等主要因素,建立刀具可靠性评估的三参数Weibull比例危险模型。模型含有6个参数,用常见的极大似然法求解时会产生含有6个变量的复杂方程组,且方程组没有封闭的解析解,需借助如迭代法的某一数值解法,计算量偏大。另一方面,根据Nelson[24]累积失效原理可知,刀具失效是在不同加工条件下累积失效的结果。据此,可以把刀具在不同加工条件下的工作时间折合在同一加工条件下对其进行可靠性分析。所以,本文基于Nelson累积失效原理,采用贝叶斯仿真方法估计模型参数,可避免求解复杂的方程组,减少了计算量。最后,结合实际案例给出了刀具变加工条件下的可靠度及故障率,解决了刀具在变加工条件下的可靠性分析难题,为刀具置换提供了理论指导。

1　刀具三参数Weibull比例危险模型

若刀具故障时间t服从三参数Weibull分布,则基准故障率和可靠度函数分别为

h0(t)=λβ(t-γ)β-1

(1)

R0(t)=exp[-λ(t-γ)β]

(2)

式中:λ、β、γ分别为Weibull分布尺度参数、形状参数及位置参数。

式(1)和式(2)未包含切削速度v、进给量f、切削深度a等参数,即三参数Weibull分布模型未考虑刀具切削用量等主要因素对刀具故障率及可靠性的影响。Cox比例危险模型[25-26]以单一统计分布模型的故障率或可靠度为基准,并结合了其他物理因素,克服了这种单一统计分布模型的上述缺点。因此,以三参数Weibull分布模型的故障率为基准故障率h0(t),综合考虑刀具切削用量等协变量Z=(v,f,a)的影响,用Cox比例危险模型描述故障时,刀具故障率为

h(t)=h0(t)exp(k,Z)=λβ(t-γ)β-1exp(k,Z)

(3)

式中:k=(k1,k2,k3)为模型参数,且

exp(k,Z)=exp(k1lnv+k2lnf+k3lna)=vk1fk2ak3

(4)

由比例危险模型可靠度和基准可靠度关系R(t)=R0(t)exp(k,Z)及式(2)、式(4)可知,刀具可靠度为

R(t)=exp[-λ(t-γ)βexp(k,Z)]=

exp[-λ(t-γ)βvk1fk2ak3]

(5)

相应的分布函数为

F(t)=1-R(t)=1-exp[-λ(t-γ)βvk1fk2ak3]

(6)

因此,由式(3)、式(5),得刀具寿命概率密度函数为

f(t)=h(t)R(t)=

λβ(t-γ)β-1vk1fk2ak3exp[-λ(t-γ)βvk1fk2ak3]

(7)

所以,不同切削用量下刀具故障时间ti(i=1,2,…,n)的似然函数为

(8)

式(8)两边取自然对数,得对数似然函数为

(9)

式(9)含有λ、β、γ、k1、k2、k3等6个未知变量,对式(9)各变量求偏导数并令其为0,会产生含有6个参数的方程组。该方程组通常没有封闭的解析解,常用数值方法求解,计算量较大,因此可结合模型参数的先验分布用贝叶斯仿真方法估计[13,27-28]。该仿真方法的思想如下:为了估计模型参数,可结合模型参数的先验分布及似然函数,应用贝叶斯原理,从参数满足后验分布中重复抽样产生所估计参数,直至找到稳定的马尔科夫链,然后舍弃过渡期抽样值,取收敛抽样均值即为参数估计值。贝叶斯仿真方法结合参数验前经验,消除了模型的不确定性,所得结果更加接近真实值,同时也避免了方程组的求解,减少了计算量。

2　刀具变加工条件下的可靠度及故障率

如前所述,在机床切削过程中,刀具切削用量及加工零部件不断变化,使得刀具的加工条件并非恒定不变,因此不能直接用不同加工条件下的工作时间进行可靠性分析。设刀具开始加工时间为t0,在m个不同加工条件末的加工时间分别为t1,t2,…,tm(m≥2,t0=0),则刀具在第m个加工条件末,顺序经历了m个加工条件,那么在第m个加工条件下的工作时间Δtm=tm-tm-1。若刀具在此时失效,则其失效是在m个不同加工条件下累积失效的结果。所以,用Nelson提出的累积失效模型[24],可以把刀具在m个不同加工条件下的工作时间折合在同一加工条件下对其进行可靠性分析。

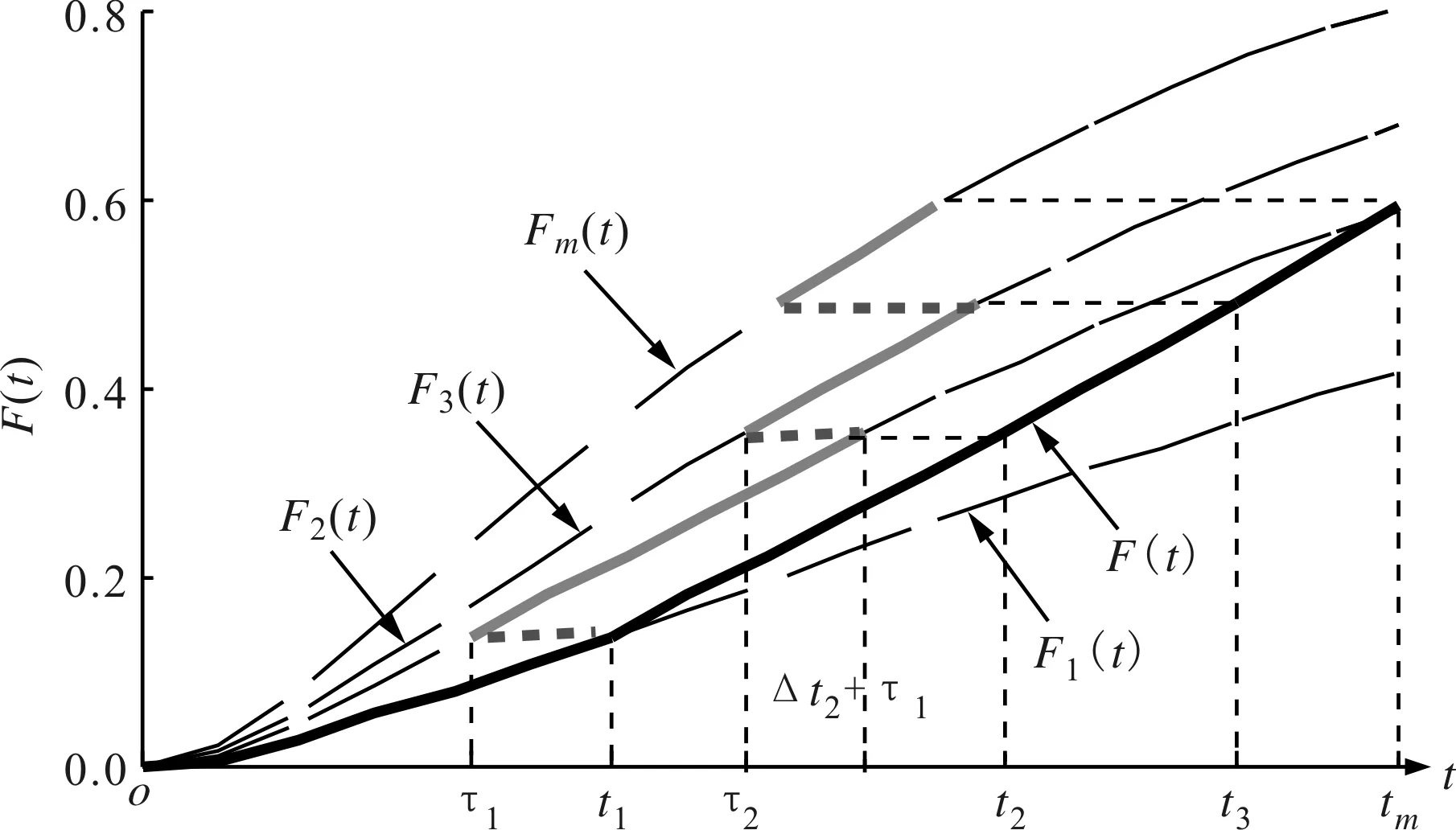
图1　累积失效模型分布函数

累积失效模型广泛应用于产品的加速寿命试验中,该模型假设产品的剩余寿命仅依赖于当时已累积失效部分和当时的应力水平,与累积方式无关。因此,刀具在第1个加工条件下工作t1时间的累积失效概率F1(t1)应与在第2个加工条件下工作某一段时间τ1的累积失效概率F2(τ1)相等,即F1(t1)=F2(τ1),如图1所示。换言之,刀具在第1个加工条件下的工作时间t1相当于在第2个加工条件下的工作时间τ1。所以,刀具在经历了2个不同的工作条件下的累积工作时间,相当于刀具只在第2个加工条件下的工作时间为Δt2+τ1,该时间折合到第3个加工条件下的工作时间τ2可由F2(Δt2+τ1)=F3(τ2)给出。不失一般性,前m-1个加工条件下的所有工作时间折合到只在第m个加工条件下的工作时间τm-1可由Fm-1(Δtm-1+τm-2)=Fm(τm-1)(τ0=0)递推获得。

可见,在整个加工过程中,刀具的分布函数F(t)为分段函数,其表达式如下

(10)

不失一般性,结合式(6)和式(10)最后一项,得

式中:Δtm-1=tm-1-tm-2(m≥2,t0=0)。令j=m-1,则化简后得刀具在第j(j=1,2,…,m)个变加工条件下的折合工作时间τj为

τj=γ+(tj-tj-1+τj-1-γ)·

(11)

式中:τ0=0。因此,由式(5)和式(10)最后一项,得刀具在第j个加工条件下的可靠度为

Rj(t)=R(t-tj-1+τj-1)=

tj-1≤t≤tj,t0=0,τ0=0,j=1,2,…,m

(12)

由式(3)得相应的故障率为

hj(t)=h(t-tj-1+τj-1)=

tj-1≤t≤tj,t0=0,τ0=0,j=1,2,…,m

(13)

3　案例分析

文献[18-19]分析了表1所示刀具寿命数据,认为刀具寿命服从两参数Weibull分布,但经分析计算发现,该组数据服从三参数Weibull分布。文献[18-19]中切削速度v、进给量f及切深a的单位分别为英尺/分钟(fpm),英寸/转(ipr),英寸(inches),结合金属机械加工工程背景,现将其分别改为m/min、mm/r、mm。

AIC、BIC信息准则是可靠性评估模型选择的常用标准[29],其值分别为

vAIC=-2max lnL+2m

vBIC=-2max lnL+mlnn

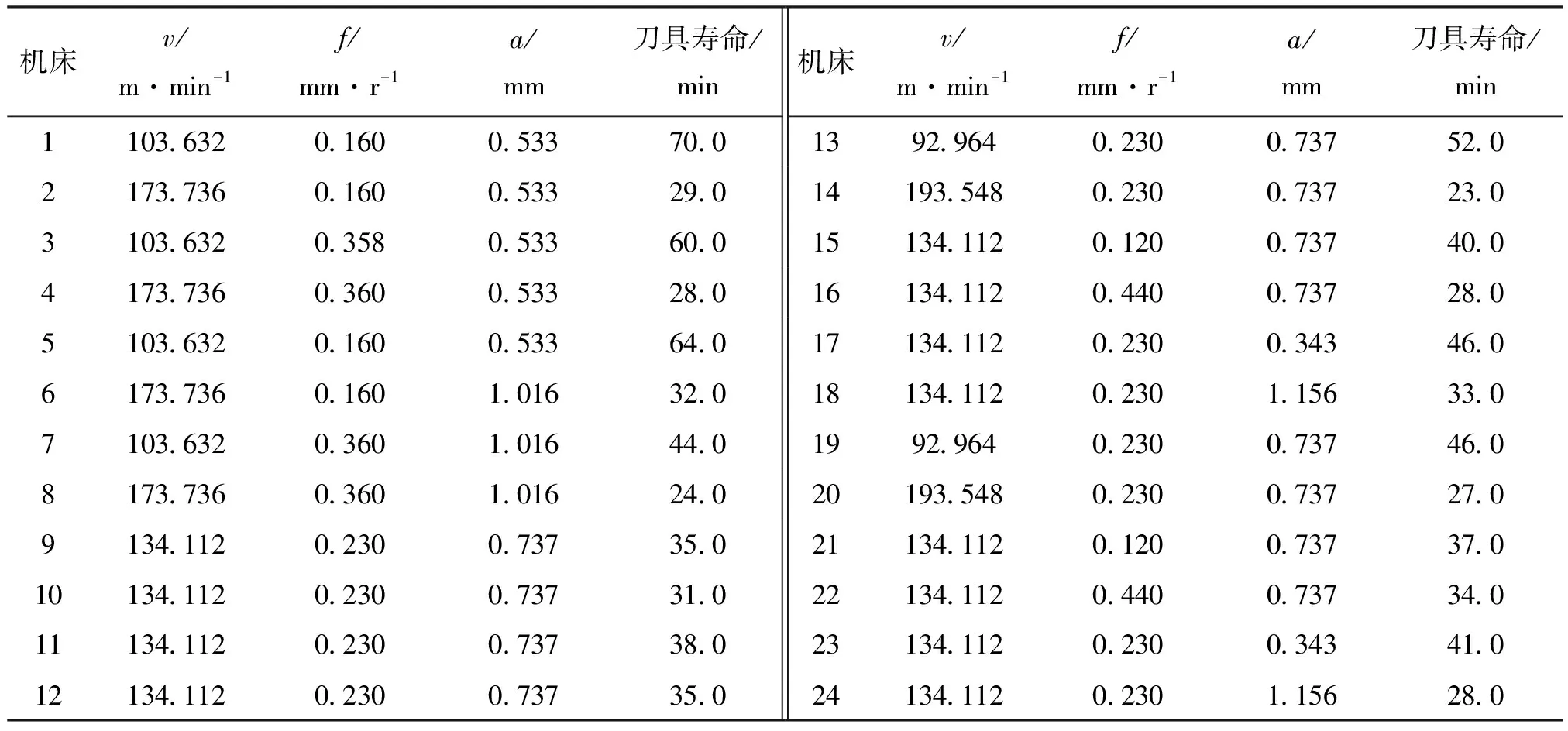
表1　机床刀具切削用量及刀具寿命

式中:m为模型参数个数;n为故障数据个数;lnL为对数似然函数。不同模型的刀具寿命如表2所示,vAIC、vBIC越小表明模型的拟合度越高。

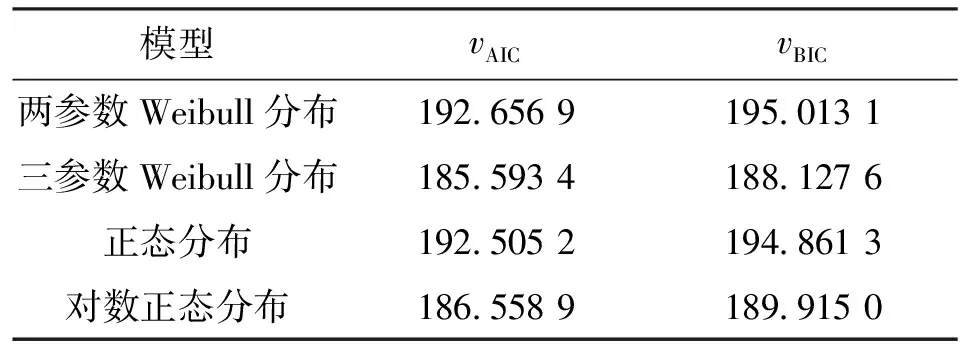
表2　刀具寿命统计分布选择比较

从表2可见,在两参数Weibull分布等众多分布模型中,三参数Weibull分布模型的vAIC、vBIC值均最小,表明三参数Weibull分布模型是描述刀具故障的最佳模型。因此,应用三参数Weibull比例危险模型,综合切削用量等协变量对刀具寿命的影响,采用贝叶斯仿真方法得到模型参数点估计和区间估计及各种误差如表3所示。

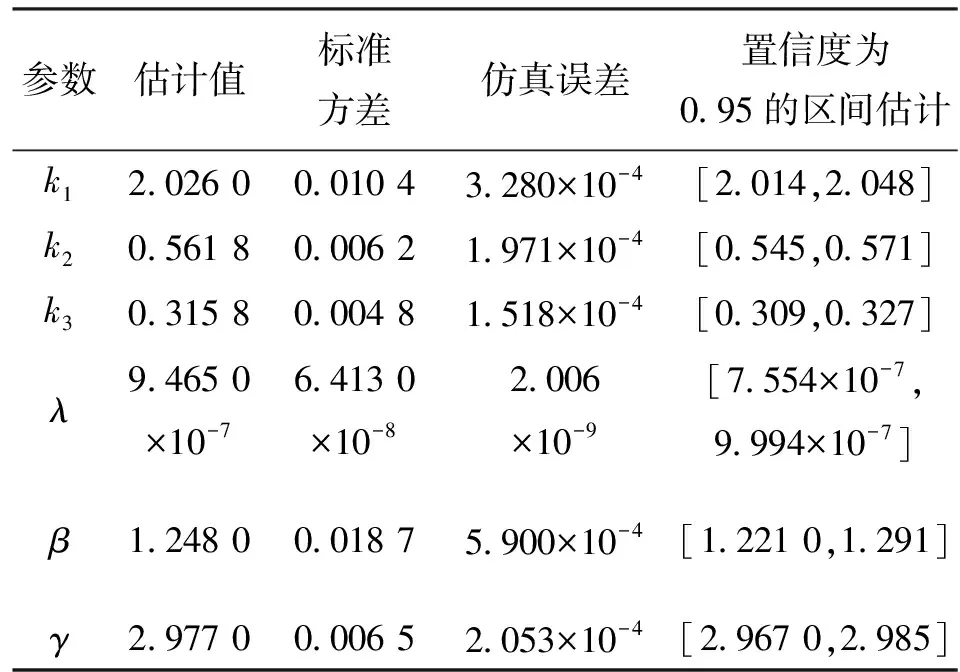
表3　切削刀具可靠性模型参数的贝叶斯估计

表4为变加工条件下刀具的顺序加工时间及切削用量。应用所提方法,根据式(11)得折合的等量切削时间分别为τ1=21.07 min,τ2=38.49 min,τ3=40.69 min。4个不同加工条件下的累积分布函数如图2所示。

在变加工条件下,刀具的可靠度及故障率均为分段函数,如在最后一个加工条件末t=80 min处,由式(12)和式(13)知其可靠度和故障率分别为

表4　变加工条件顺序加工时间及切削用量

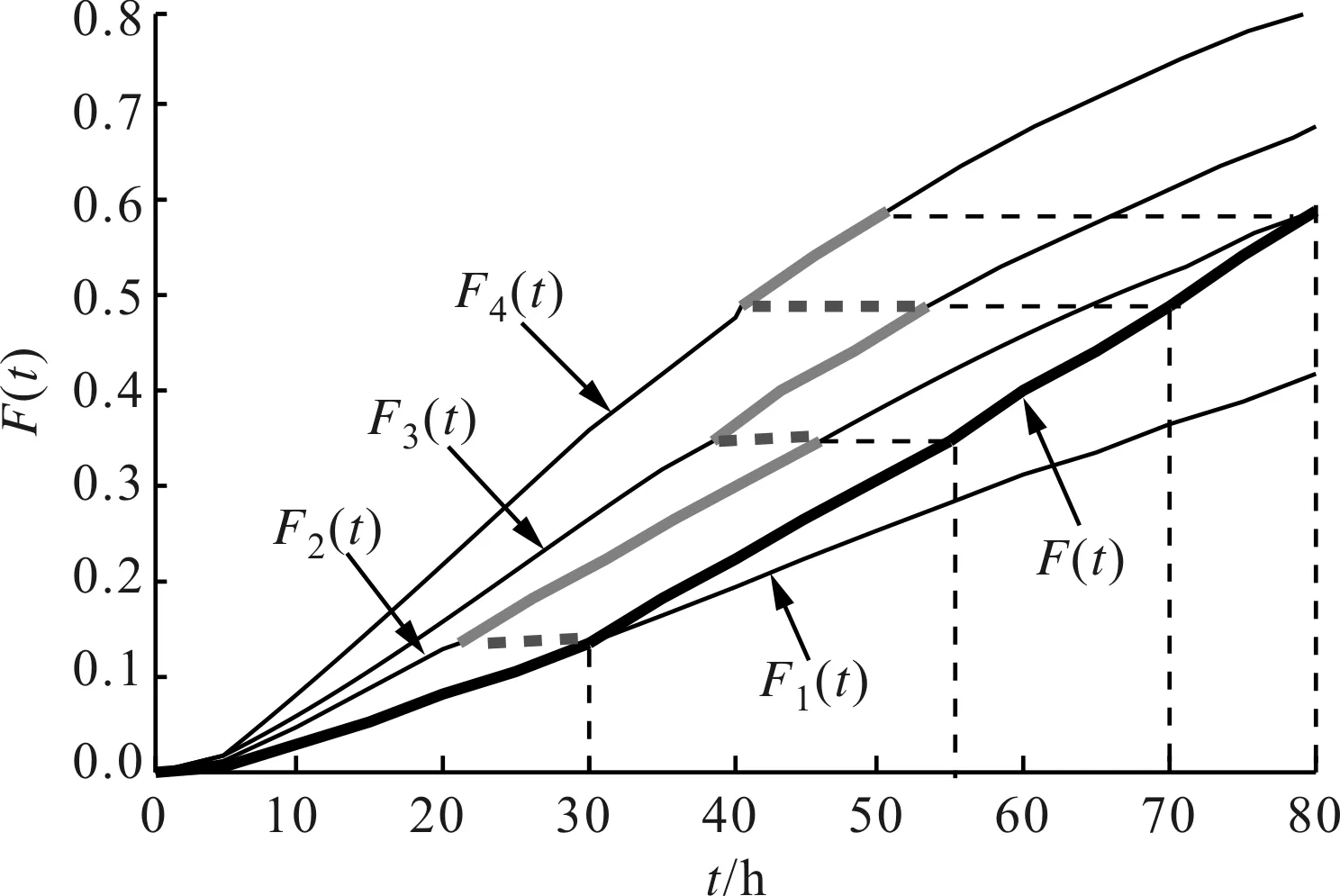
图2　变加工条件下刀具累积分布函数

可见,在最后一个加工条件末刀具可靠度已很低。此时,若不能满足生产要求,应根据最小可靠度或最高故障率进行置换。

所有不同加工条件下的刀具可靠度及故障率分别如图3和图4所示。图3显示在不同加工时间分界点,即上一加工时间末和下一加工时间开始点,刀具的可靠度相同,如R1(30)=R2(30)。在整个加工过程中,刀具可靠度函数分段连续单调下降,但刀具故障率在分界时间点表现为突变上跳,其函数为分段不连续单调增加。该特点和恒定加工条件下刀具可靠度单调非分段连续下降及故障率连续单调递增有所不同,表现出不同加工条件对刀具故障率的显著影响。如在本案例中的第4、第3两个不同加工条件下的时间分界点t=70 min处,刀具故障率之比为

刀具在其他分界点的故障率之比分别为h2(30)/h1(30)=1.494、h3(55)/h2(55)=1.213 5。可见,刀具在30、55、70 min 3个不同加工时间分界点的故障率分别增长49.40%、21.35%、33.94%,表现出刀具加工条件受切削用量、加工部位及不同类型等因素的影响。事实上,由式(5)、式(11)和式(12)可得

(14)

同样,直接由式(5)和式(12),得

Rj(tj)=R(tj-tj-1+τj-1)=

(15)

比较式(14)和式(15),有

Rj(tj)=Rj+1(tj),j=1,2,…,m

可见,在不同加工时间分界点上可靠度相等,即其可靠度函数是连续的。

对于故障率,有

(16)

由于切削用量的变化,式(16)显然不相等。本案例中hj+1(tj)/hj(tj)(j=1,2,3)均大于1,其故障率在3个不同加工分界点均为突变上跳,但需要指出的是,式(16)有可能小于1,即故障率在时间分界点也有可能突变下跳。

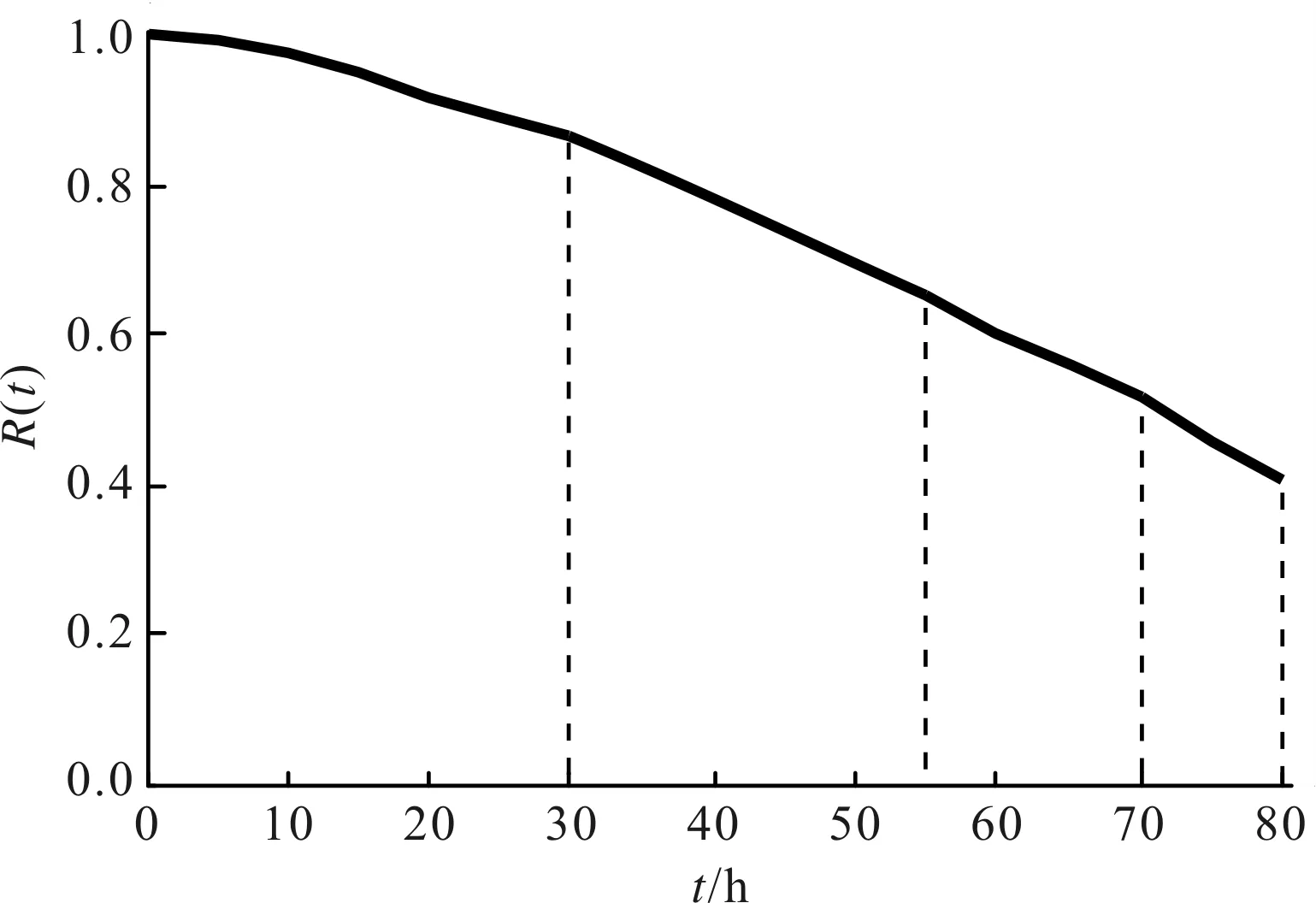
图3　所有不同加工条件下的刀具可靠度的规律

图4　所有不同加工条件下的刀具故障率的规律

4　结　论

综合统计分布模型和影响刀具寿命的切削用量等物理因素,在分析两参数Weibull分布等单一统计分布概率模型的基础上,建立了刀具可靠性评估的三参数Weibull比例危险模型。基于该模型,利用Nelson累积失效原理,确定了不同加工时间在同一加工条件下的折合时间。结合贝叶斯仿真模型参数估计方法,揭示了刀具在变加工条件下的可靠度和故障率的变化规律,为更换不合格刀具提供了理论依据。与恒定加工条件下刀具的可靠性(故障率)为单调连续下降(上升)不同,在变加工条件下,刀具可靠度及故障率函数均为分段函数,前者为分段连续单调递减,后者因受切削用量等的影响,表现为分段不连续单调递增,且在不同加工条件时间分界点突变上跳或下跳。

参考文献:

[1]CHEN J S. Optimization models for the tool change scheduling problem [J]. Omega, 2008, 36(5): 888-894.

[2]LETOT C, SERRA R, DOSSEVI M, et al. Cutting tools reliability and residual life prediction from degradation indicators in turning process [J]. International Journal of Advanced Manufacturing Technology, 2016, 86(1/2/3/4): 495-506.

[3]SALONITIS K, KOLIOS A. Reliability assessment of cutting tool life based on surrogate approximation methods [J]. International Journal of Advanced Manufacturing Technology, 2014, 71(5/6/7/8): 1197-1208.

[4]CHOUDHURY S K, APPA RAO I V K. Optimization of cutting parameters for maximizing tool life [J]. International Journal of Machine Tools and Manufacture, 1999, 39(2): 343-353.

[5]ORABY S E, HAYHURST D R. Tool life determination based on the measurement of wear and tool force ratio variation [J]. International Journal of Machine Tools & Manufacture, 2004, 44(12): 1261-1269.

[6]IAKOVOU E, IP C M, KOULAMAS C. Optimal solutions for the machining economics problem with stochastically distributed tool lives [J]. European Journal of Operational Research, 1996, 92(1): 63-68.

[7]KWON W T, PARK J S, KANG S. Effect of group IV elements on the cutting characteristics of Ti(C, N) cermet tools and reliability analysis [J]. Journal of Materials Processing Technology, 2005, 166(1): 9-14.

[8]GALANTE G, LOMBARDO A, PASSANNANTI A. Tool-life modelling as a stochastic process [J]. International Journal of Machine Tools & Manufacture, 1998, 38(10/11): 1361-1369.

[9]樊宁, 艾兴, 邓建新. 陶瓷刀具的磨损寿命可靠性 [J]. 机械工程学报, 2002, 38(4): 30-35.

FAN Ning, AI Xing, DENG Jianxin. Reliability of ceramic cutting tool life by wear [J]. Chinese Journal of Mechanical Engineering, 2002, 38(4): 30-35.

[10] 陈保家, 陈雪峰, 李兵, 等. Logistic回归模型在机床刀具可靠性评估中的应用 [J]. 机械工程学报, 2011, 47(18): 158-164.

CHEN Baojia, CHEN Xuefeng, LI Bing, et al. Reliability estimation for cutting tool based on logistic regression model [J]. Chinese Journal of Mechanical Engineering, 2011, 47(18): 158-164.

[11] LETOT C, SERRA R, DOSSEVI M, et al. Cutting tools reliability and residual life prediction from degradation indicators in turning process [J]. The International Journal of Advanced Manufacturing Technology, 2016, 86(1): 495-506.

[12] DING Feng, HE Zhengjia. Cutting tool wear monitoring for reliability analysis using proportional hazards model [J]. International Journal of Advanced Manufacturing Technology, 2011, 57(5/6/7/8): 565-574.

[13] 张石平, 王智明, 杨建国. 机床刀具可靠性及寿命评估 [J]. 计算机集成制造系统, 2015, 21(6): 1579-1584.

ZHANG Shiping, WANG Zhiming, YANG Jianguo. Tool reliability and life assessment for machine tools [J]. Computer Integrated Manufacturing Systems, 2015, 21(6): 1579-1584.

[14] CAI Gaigai, CHEN Xuefeng, LI Bing, et al. Operation reliability assessment for cutting tools by applying a proportional covariate model to condition monitoring information [J]. Sensors, 2012(12): 12964-12987.

[15] 李常有, 张义民, 王跃武. 恒定加工条件及定期补偿下的刀具渐变可靠性灵敏度分析方法 [J]. 机械工程学报, 2012, 48(12): 162-168.

LI Changyou, ZHANG Yimin, WANG Yuewu. Gradual reliability and its sensitivity analysis approach of cutting tool in invariant machining condition and periodical compensation [J]. Chinese Journal of Mechanical Engineering, 2012, 48(12): 162-168.

[16] LI Changyou, ZHANG Yimin. Time-variant reliability assessment and its sensitivity analysis of cutting tool under invariant machining condition based on Gamma process [J]. Mathematical Problems in Engineering, 2012(1): 542-551.

[17] ORAL A, CAKIR M C, GONEN D, et al. Experimental investigation of a novel machining strategy for rough turning using variable feed rate [J]. The International Journal of Advanced Manufacturing Technology, 2016, 87(1): 779-787.

[18] LIU H, MAKIS V. Cutting-tool reliability assessment in variable machining conditions [J]. IEEE Transactions on Reliability, 1996, 45(4): 573-581.

[19] LIU H, MAKIS V, JARDINE A K S. Scheduling of the optimal tool replacement times in a flexible manufacturing system [J]. IIE Transactions, 2001, 33(6): 487-495.

[20] RODRIGUEZ C E P, SOUZA G F M. Reliability concepts applied to cutting tool change time [J]. Reliability Engineering and System Safety, 2010, 95(8): 866-873.

[21] ARAMESH M, SHABAN Y, YACOUT S, et al. Survival life analysis applied to tool life estimation with variable cutting conditions when machining titanium metal matrix composites (Ti-MMCs) [J]. Machining Science & Technology, 2016, 20(1): 132-147.

[22] 郑锐. 三参数威布尔分布参数估计及在可靠性分析中的应用 [J]. 振动与冲击, 2015, 34(5): 78-81.

ZHENG Rui. Parameter estimation of three-parameter Weibull distribution and its application in reliability analysis [J]. Journal of Vibration and Shock, 2015, 34(5): 78-81.

[23] DJEDDI A Z, HAFAIFA A, SALAM A. Operational reliability analysis applied to a gas turbine based on three parameter Weibull distribution [J]. Mechanika, 2015, 21(3): 187-192.

[24] NELSON W. Accelerated life testing-step-stress models and data analyses [J]. IEEE Transactions on Reliability, 1980, 29(2): 103-108.

[25] COX D R. Regression models and life tables (with discussion) [J]. Journal of the Royal Statistical Society: Series BMethodological, 1972, 34(2): 187-220.

[26] MERRICK J R W, SOYER R, MAZZUCHI T A. A Bayesian semiparametric analysis of the reliability and maintenance of machine tools [J]. Technometrics, 2003, 45(1): 58-69

[27] JIANG H, XIE M, TANG L C. Markov chain Monte Carlo methods for parameter estimation of the modified Weibull distribution [J]. Journal of Applied Statistics, 2008, 35(6): 647-658.

[28] JAHEEN Z F, HARBI M M A. Bayesian estimation for the exponentiated Weibull model via Markov chain Monte Carlo simulation [J]. Communications in Statistics-Simulation and Computation, 2011, 40(4): 532 -543.

[29] 王智明, 杨建国, 王国强, 等. 多台数控机床的时间截尾可靠性评估 [J]. 哈尔滨工业大学学报, 2011, 43(3): 85-89.

WANG Zhiming, YANG Jianguo, WANG Guoqiang, et al. Reliability evaluation of multiple NC machine tools with time truncation [J]. Journal of Harbin Institute of Technology, 2011, 43(3): 85-89.