采用不同管排组合的换热器弹性管束壳程流体诱导振动响应
2018-04-18季家东葛培琪毕文波刘萍
季家东, 葛培琪, 毕文波, 刘萍
(1.安徽理工大学机械工程学院, 232001, 安徽淮南; 2.山东大学机械工程学院, 250061, 济南)
弹性管束换热器[1-3]利用内部流体所诱导的弹性管束振动,在实现不同温度的壳程、管程流体间强化传热的同时,为无源强化传热技术在换热器中的应用开辟了新的研究方向[4-5]。高效弹性管束换热器的设计应遵循的准则[6]是:在满足强化传热的参数范围内,对弹性管束的振动进行合理激发和有效控制,同时兼顾管束的疲劳寿命,确保其在强化传热的同时能长期运行不致破坏。这样,对弹性管束在壳程或管程流体诱导下的振动响应机理进行深入研究就成为高效弹性管束换热器设计的关键[6]。弹性换热器内的流体诱导振动是一个复杂的流固耦合问题,而现阶段的相关研究大多采用实验手段,具有很大的局限性[7]。对于换热器内多排弹性管束在壳程流体诱导下的振动响应进行分析,对进一步研究强化传热机理、改进管束结构及实现振动的合理激发和有效控制等都具有重要意义。
基于弹性管束换热器的工作原理,闫柯等对一种新型空间锥螺旋弹性管束进行了数值模拟和实验研究,发现在一定流速条件下,新型空间锥螺旋弹性管束的振幅增加缓慢,当流速超过某一值时,振幅随着流速的增加而迅速增大,而空间锥螺旋弹性管束的模态频率则随流速的增加而减小[8-9]。季家东等采用流固耦合的顺序求解法,研究了单排/多排弹性管束在均匀壳程流体或/和管程流体诱导下的振动响应,结果表明:弹性管束的振动主要由壳程流体诱导所致,两不锈钢连接体主要表现为面内振动,流速较低时存在明显的2倍谐频;均匀壳程流体诱导多排弹性管束振动时,迎流部分弹性管束的振动强度较大、频率较高,背流部分弹性管束的振动强度较小、频率较低,且各排弹性管束间的振动相互影响[10-12]。
本文以整体弹性管束换热器为研究对象,利用通用CFD分析软件CFX和ANSYS Workbench软件的瞬态动力学分析模块,采用流固耦合的顺序求解法对不同管排间距和管排数条件下多排弹性管束的振动响应进行了数值研究。
1 数值计算方法
1.1 几何模型
图1所示为弹性管束换热器及其壳程流体域示意图,其中:换热器筒体尺寸为Φ325 mm×10 mm;管程流体导入和导出管的尺寸为Φ45 mm×3 mm;壳程流体导入管尺寸为Φ60 mm×3 mm;壳程流体导出管尺寸为Φ73 mm×4 mm。

图1 弹性管束换热器及其壳程流体域示意图
除弹性管束外,换热器的其余各部分均由优质普通钢制成。管程流体导入、导出管和壳程流体导入管均焊接在下封头上,壳程流体导出管焊接在上封头上,其余各部分间均由螺栓连接。
图2所示为由4根紫铜弯管(半径分别为R1、R2、R3、R4,外径为d,壁厚为δ)和2个不锈钢连接体(Ⅲ、Ⅳ)组成的弹性管束的几何结构示意图,各排弹性管束通过Ⅰ、Ⅱ两端均匀固定在壳程流体导入、导出管上,管排间距为H,管排数为n。
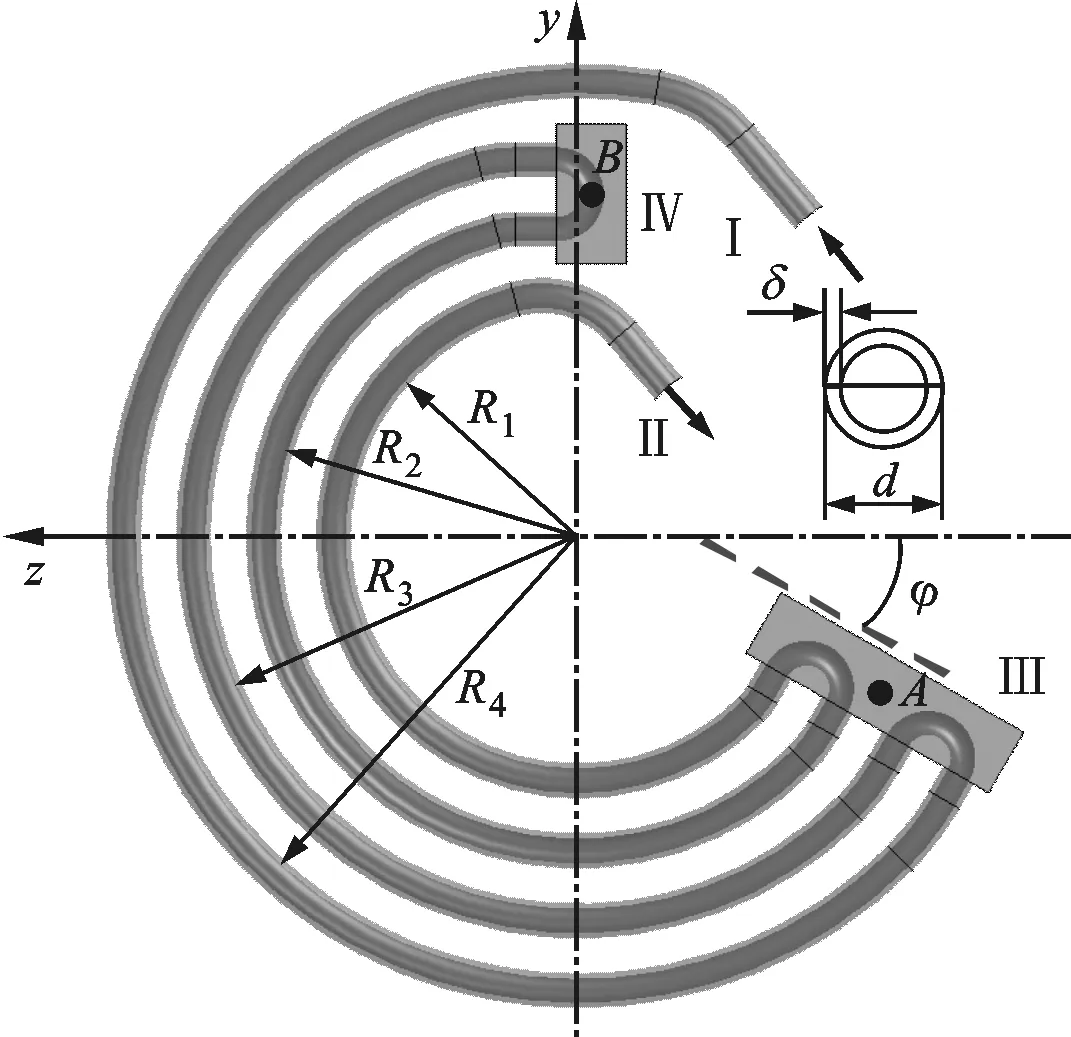
图2 弹性管束结构示意图
计算过程中,取弯管半径R1=70 mm,R2=90 mm,R3=110 mm,R4=130 mm;连接体Ⅲ和Ⅳ的尺寸分别为80 mm×20 mm×20 mm和40 mm×20 mm×20 mm;管束外径d=10 mm;管束壁厚δ=1.5 mm;夹角φ=45°;管排间距H=40,50,60,70 mm;管排数n=6,12。
为便于分析,换热器内的弹性管束由下至上依次编号为1,2,…。为了监测各排弹性管束在壳程流场诱导下的振动响应,在每排弹性管束2个不锈钢连接体上分别设置监测点Ai、Bi(i=1,2,…)。
1.2 网格划分
因换热器内各排弹性管束由弹性材料制成,在流体的诱导下较易产生振动,而换热器外壳,壳程流体导入管和管程流体导入、导出管均为钢结构,在流体诱导下基本不产生振动。为提高计算效率,在不影响计算结果的前提下,结构域部分仅保留各排弹性管束。
单排弹性管束的网格划分策略如图3所示,图中A、B两点是设立的监测点。从图3可以看到,每排弹性管束网格由四面体网格(不锈钢连接体)和六面体网格(紫铜弯管)组成,共9 366个单元、54 777个节点,最低网格质量为0.42。

图3 单排弹性管束网格划分策略
为便于进行网格划分,将壳程流体域分割为如图1所示的6个部分,各部分的网格分割域如图4所示。仅下封头域采用四面体网格,其余各分割域均采用六面体网格。为提高计算精度,管束周围流体域采用大密度网格,并布置6层边界层网格。

(a)上封头域 (b)下封头域 (c)管束域
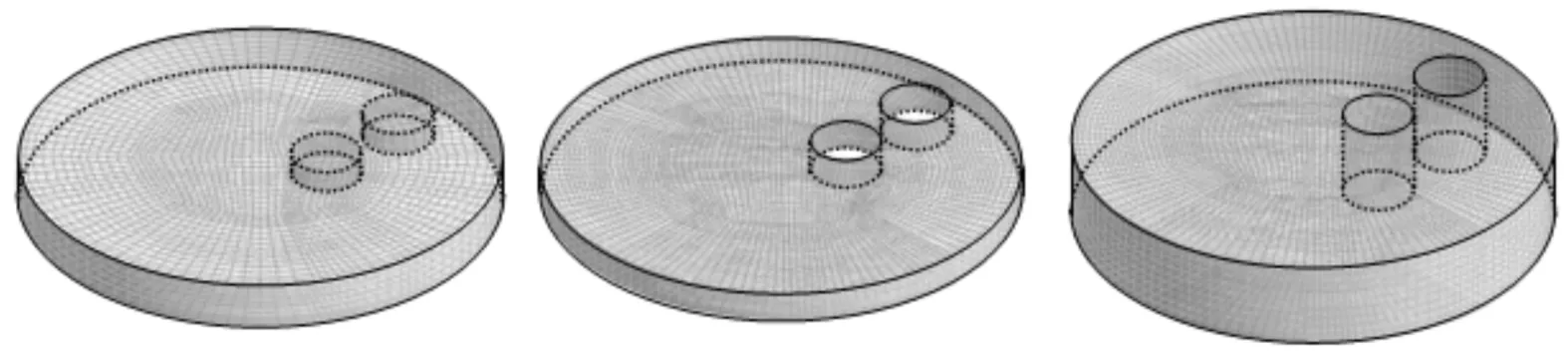
(d)上接域 (e)中接域 (f)下接域图4 弹性管束网格分割域
表1所示为各分割域的网格数量和质量,可知最低网格质量为0.36,出现在上封头域,为非流固耦合(FSI)计算区域,对计算结果基本无影响。
整体壳程流体域网格在CFX软件中通过复制、平移和连接形成,各分割域间的网格连接均采用通用网格界面(GGI)的方式。

表1 各分割域的网格数量和质量
这样,以管排间距H=60 mm的六排弹性管束换热器为例,壳程流体域总单元数
ne=58 932+175 249+203 578×6+
19 784+32 322×5+51 872=1 688 915
(1)
壳程流体域总节点数
nd=53 868+30 918+186 520×6+
16 929+27 390×5+46 370=1 404 155
(2)
这种流体域分割的网格划分策略,大幅提高了网格划分的精度、效率和灵活性。通过改变中接域的高度,可组装成不同管排间距的壳程流体域;通过改变管束域和中接域的复制数量,可组装成任意管排数的壳程流体域。
1.3 数值分析方法
基于本文的研究问题,将求解域分成壳程流体域和结构域,流-固耦合(FSI)求解采用顺序求解法在每个时间步长内独立进行,通过建立FSI交界面实现流体域和结构域间的数据传递。
壳程流体域采用CFX软件进行计算,流体介质为水,入口流速v为0.2 m/s或0.4 m/s(Re>2 300),属湍流流动,选用标准k-ε模型进行计算。边界条件设置:入口边界类型为Inlet,给定入口速度0.4 m/s;出口边界类型为Outlet,设置出口相对静压为0 Pa,计算环境设置为标准大气压(101.325 kPa);流体域内部与管束接触面设置为FSI交界面。
结构域采用ANSYS Workbench软件的瞬态动力学分析模块进行计算。边界条件设置:2个固定端I、II处截面为固定约束;各排弹性管束的外表面为FSI交界面,与流体域FSI交界面相对应;重力加速度为-x方向,取值为9.806 6 m/s2。
图5所示为双向FSI计算的基本流程,具体实施过程如下。

图5 双向FSI计算的基本流程
(1)基于初始边界条件,采用CFX求解器进行流体域计算,得到流体域FSI交界面的应力。
(2)将求解的应力传递到结构域FSI交界面,以此为初始条件采用ANSYS求解器对结构域进行瞬态动力学计算,得到结构域FSI交界面的位移。
(3)将求解的位移反向传递到流体域FSI交界面,基于新的边界条件进行下一个时间步长内流体域的计算。
(4)交替迭代,直至完成。
因网格较多,且FSI计算耗时,为得到壳程流场充分发展条件下弹性管束的振动响应,计算采用可大幅提高计算效率的粗算加精算的分步计算策略,具体步骤如下。
第1步:粗算,采用CFX软件对壳程流体域进行计算,直到内部流场获得充分发展。
第2步:精算,以粗算结果为初始条件进行FSI计算,直至监测点振动达到稳定,此时的振动响应即为壳程流场充分发展条件下弹性管束的振动响应。
1.4 结果验证
为进行网格独立性分析,基于3种不同的网格划分方案,对v=0.4 m/s时六管束换热器最底排弹性管束监测点在x方向的振动幅值Ax和频率fx进行了计算,结果如表2所示。
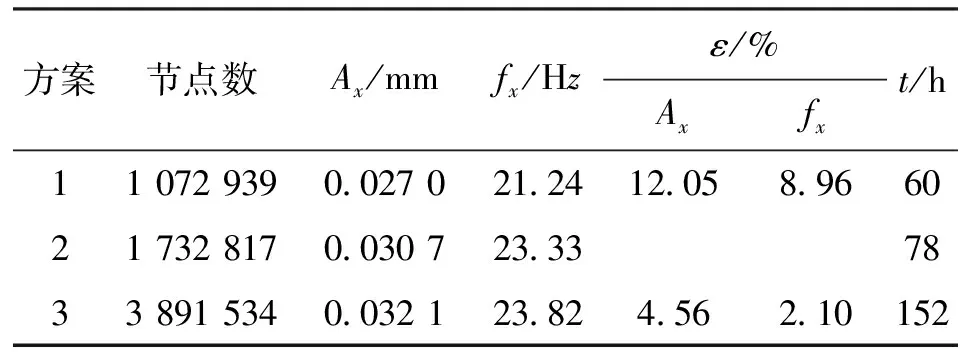
表2 网格独立性分析计算结果
ε:相对误差,以方案2的计算结果为基准;t:计算时间。
表2中,节点数为整个求解域的总节点数,方案2为上面提到的网格划分策略。兼顾计算精度和计算效率,选择方案2的网格作为计算用网格满足独立性要求。
为验证数值计算方法的正确性和准确性,利用文献[2]中实验用弹性管束的结构参数,建立与之相应的单排管束计算模型,对不同入口流速时2个监测点x方向的振动频率fx和加速度ax进行了计算,数值计算结果与实验测试结果的对比如表3所示。

表3 数值计算结果与实验测试结果的对比
由表3可知,数值计算结果与实验测试结果基本一致,虽然加速度的相对误差较大,但并未超过10%,由此验证了数值计算方法的正确性和准确性。
2 结果与讨论
2.1 振动响应分析
图6所示为监测点A1在x方向的位移(Sx)随FSI计算时间(tc)的变化。计算中如无特别说明,流体介质为水,v=0.4 m/s,H=60 mm,n=6。
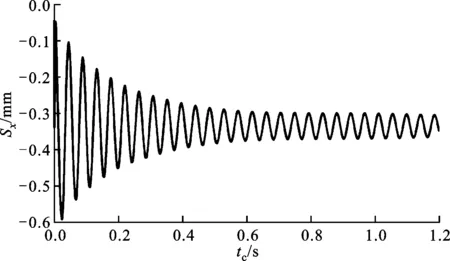
图6 位移随FSI计算时间的变化
从图6可以看到,随着FSI计算时间的增加,振动幅值逐渐减小并趋于稳定,当FSI计算时间tc=0.6 s时振动基本达到稳定,此时的振动响应即为壳程流场充分发展条件下监测点的振动响应。
表4所示为最底排(编号为1)和最顶排(编号为6)弹性管束监测点在不同方向的振动幅值和频率,从中可以看到:
(1)连接体Ⅲ上监测点的振幅较大、频率较低,连接体Ⅳ上监测点的振幅较小、频率较高,各排弹性管束同一连接体上的监测点在各方向的振动频率均一致,但幅值不同,这是因为在换热器内部结构的影响下,连接体Ⅲ所在区域流体的流动速度较高所致;
(2)各监测点的振动均以x方向的振动为主,说明弹性管束的振动主要表现为面外振动,这是因为流经弹性管束的流体速度沿x方向的分量较小,振动主要体现为纵向流诱振,使得沿弹性管束平面方向的振动幅值较大。
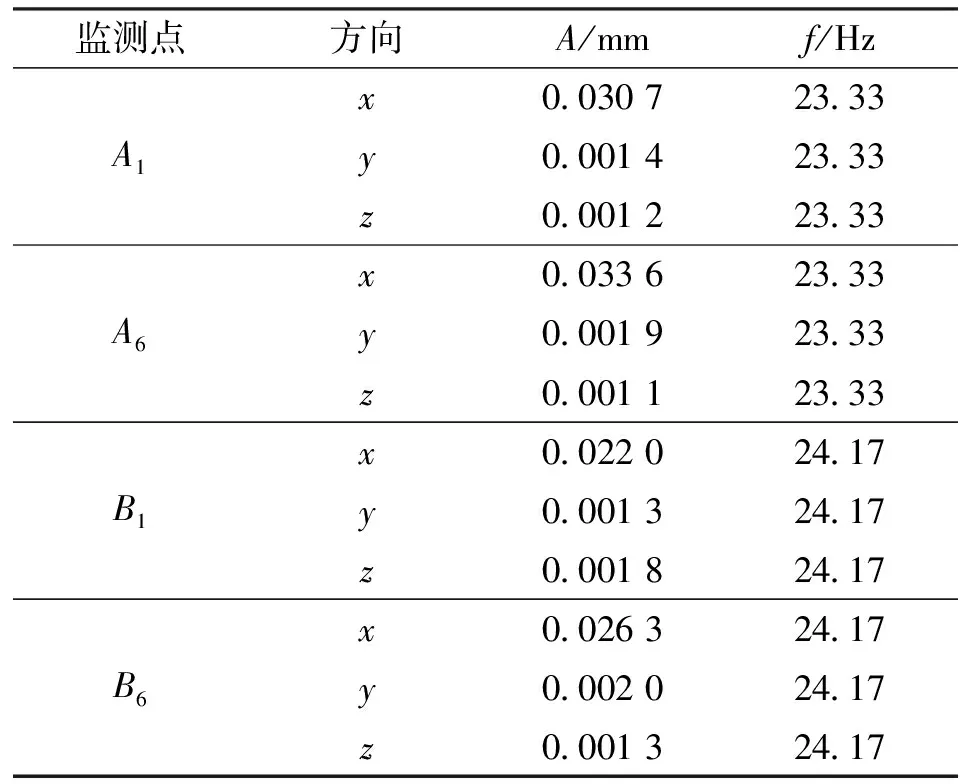
表4 监测点各方向的振幅和频率
表5所列为不同入口流速条件下,各排弹性管束上的2个监测点在x方向的振幅Ax随管束编号的变化数据,分析可知:
(1)各排弹性管束在相同监测点的最大相对误差均较大,说明各排弹性管束的振动不均匀,随着管束编号的增加,监测点振幅呈先增大后减小的趋势,这是因为流体绕流前几排管束后,生成了具有一定强度的脉动流,使得监测点的振幅逐渐增大,而随着绕流管排数的增加,流体流动的紊流性和不规则性逐渐增强,从而导致监测点的振动强度逐渐降低;
(2)各排弹性管束连接体Ⅲ的振幅均大于连接体Ⅳ的振幅,说明连接体Ⅲ的振动较剧烈,如前面所述,造成这种现象的原因是流经连接体Ⅲ所在区域的流体具有较高的流动速度。

表5 监测点振幅随管束编号的变化
注:带圆圈数字为管束编号。
综上所述,换热器内各排弹性管束存在振动不均的现象,这是影响弹性管束换热器使用寿命和传热效率的主要因素之一。结合高效弹性管束换热器的设计准则,这一结论可为进一步实现振动的合理激发和有效控制提供依据。
2.2 管排间距对振动响应的影响
通过改变中接域的高度,并利用CFX软件的网格复制、平移和连接功能,可组装成不同管排间距的壳程流体域。
表6所列为不同管排间距(H=40~70 mm)条件下,最底排(编号为1)和最顶排(编号为6)弹性管束2个监测点在x方向的振幅和频率。由表6可知:
(1)随着H的增加,各监测点的频率小幅降低,幅值基本呈先增大后减小的趋势,这是因为流体绕流多排弹性管束时,间距比H/d(管排间距与管束外径之比)存在一临界值,当H/d等于临界值时,管束振动强度最高,当H/d高于或低于这一临界值时振动强度都会降低。
(2)对振幅而言,监测点Ai振幅的最大变化幅度(A1处为34.78%,A6处为48.54%)高于监测点Bi振幅的最大变化幅度(B1处为29.41%,B6处为39.89%),而对频率而言,监测点Ai的频率降幅(0.21%)低于监测点Bi的频率降幅(1.87%),因此连接体Ⅲ上监测点的振幅受H的影响较大,连接体Ⅳ上监测点的频率受H的影响较大。

表6 不同管排间距时监测点x方向的振幅和频率
图7所示为不同管排间距(H=40,70 mm)时,各排弹性管束上的监测点在x方向的振幅随管束编号的变化。

(a)不锈钢连接体Ⅲ

(b)不锈钢连接体Ⅳ图7 不同管排间距时监测点振幅随管束编号的变化
从图7可以看到:
(1)对连接体Ⅲ而言,监测点振幅在H=40 mm时的最大相对误差为44.47%,在H=70 mm时的最大相对误差为11.28%,而对连接体Ⅳ而言,监测点振幅在H=40 mm时的最大相对误差为32.81%,在H=70 mm时的最大相对误差为25.09%,这是因为当H较小时,各排管束间的相互影响较强,使得振幅随管束编号的变化较剧烈;
(2)在H取不同值时,2个监测点的振幅随管束编号的递增基本呈先增大后减小的趋势,当H较小(40 mm)时连接体Ⅲ振动的均匀性较差,当H较大(70 mm)时连接体Ⅳ振动的均匀性较差,这是由于流体域高度改变造成连接体附近流场改变引起的。
综上所述,管排间距越小,各排管束间的相互影响就越强,管束振动的均匀性越差。在进行弹性管束换热器的设计时,应综合考虑换热器的传热特性、阻力性能和使用寿命,选择合适的管排间距。
2.3 管排数对振动响应的影响
通过改变管束域和中接域的复制数量,利用CFX软件的网格复制、平移和连接功能,可组装成管排数n为12的壳程流体域。表7所列为部分弹性管束2个连接体x方向的振幅和频率。

表7 部分监测点x方向的振幅和频率
从表7可以看到:
(1)各排弹性管束同一连接体上监测点的振动频率一致,且连接体Ⅳ上监测点的振动频率较高;
(2)各排弹性管束同一连接体上监测点的振幅随管束编号的增加呈先增大后减小的趋势,且连接体Ⅲ上监测点的振幅较大。
图8所示为管排数n=6,12时,各排弹性管束上监测点在x方向的振幅变化情况,从中可以看到:
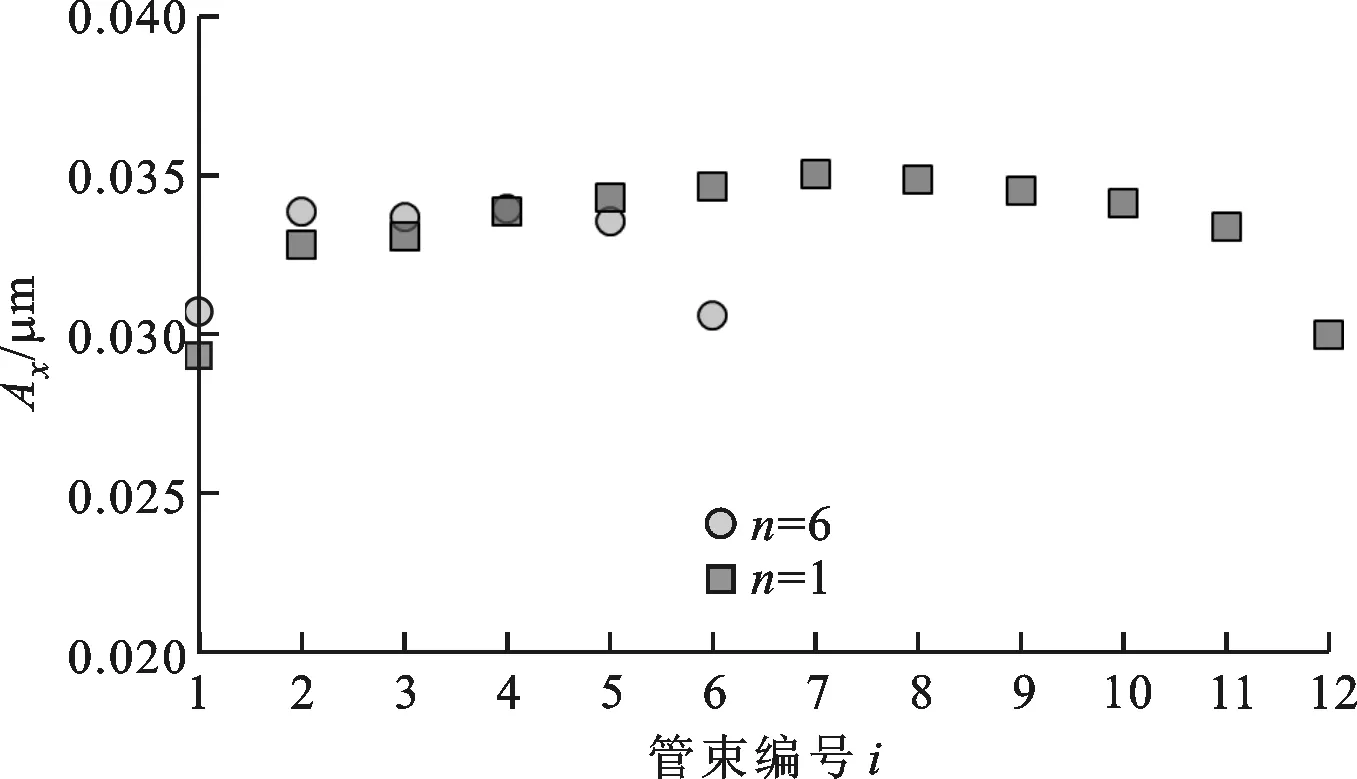
(a)不锈钢连接体Ⅲ

(b)不锈钢连接体Ⅳ图8 不同管排数时监测点振幅随管束编号的变化
(1)各排弹性管束同位置监测点的振幅随管束编号的增加先增大后减小,且这种变化趋势不受管排数的影响;
(2)与连接体Ⅳ上监测点的振幅相比,连接体Ⅲ上监测点的振幅较大,亦不受管排数的影响;
(3)对于n=12时各监测点振幅的最大相对误差来说,连接体Ⅲ的为16.53%,大于n=6时的10.00%,连接体Ⅳ的为28.70%,大于n=6时的25.17%,这说明随管排数增加,各排管束的振动不均匀性增强,因为管排数增加时壳程流体域的高度也增加,进而影响换热器内的流场分布。
综上所述,在本文的计算参数范围内,管排数不会影响内部管束振动的基本变化趋势。对于更多管排数对换热器传热特性的影响,还有待进一步探讨。
3 结 论
本文以整体弹性管束换热器为研究对象,基于流固耦合的顺序求解法,对不同管排间距和管排数条件下多排弹性管束的振动响应进行了数值研究,并通过与实验数据的对比,验证了数值求解方法的正确性和准确性。获得的主要结论如下。
(1)本文提出的粗算加精算的分步计算策略,可大幅减少计算时间,提高计算效率。
(2)在壳程流体诱导下,各监测点的振动主要表现为面外振动,且连接体Ⅲ(大连接体)的振动较剧烈;各排弹性管束的振动不均匀,监测点振幅随着管束编号的增加呈先增大后减小的趋势。
(3)当管排间距较小时,振幅随管束编号的变化较剧烈,各排管束间的相互影响较大;随着管排间距的增加,各监测点的频率小幅降低,振幅基本呈先增大后减小趋势;连接体Ⅲ上监测点的振幅受管排间距的影响较大,连接体Ⅳ(小连接体)上监测点的频率受管排间距的影响较大。
(4)各排弹性管束同位置监测点的振幅随管束编号的增加先增大后减小,连接体Ⅲ上监测点的振幅高于连接体Ⅳ上监测点的振幅,且这些变化规律不受管排数的影响;随管排数量增加,各排管束的振动不均匀性增强。
参考文献:
[1]CHENG Lin, LUAN Ting, DU Wenjing, et al. Heat transfer enhancement by flow-induced vibration in heat exchangers [J]. International Journal of Heat and Mass Transfer, 2009, 52(3): 1053-1057.
[2]宿艳彩. 弹性管束流体诱导振动及换热特性研究 [D]. 济南: 山东大学, 2012.
[3]YAN Ke, GE Peiqi, HONG Jun. Experimental study of shell side flow-induced vibration of conical spiral tube bundle [J]. Journal of Hydrodynamics, 2013, 25(5): 695-701.
[4]JI Jiadong, GE Peiqi, BI Wenbo. Numerical investigation on the flow and heat transfer performances of horizontal spiral-coil pipes [J]. Journal of Hydrodynamics, 2016, 28(4): 576-584.
[5]DUAN Derong, GE Peiqi, BI Wenbo, et al. Numerical investigation on the heat transfer enhancement mechanism of planar elastic tube bundle by flow-induced vibration [J]. International Journal of Thermal Sciences, 2017, 112: 450-459.
[6]JI Jiadong, GE Peiqi, BI Wenbo. Numerical analysis on shell-side flow-induced vibration and heat transfer characteristics of elastic tube bundle in heat exchanger [J]. Applied Thermal Engineering, 2016, 107: 544-551.
[7]季家东. 弹性管束换热器壳程分布式脉动流诱导管束振动研究 [D]. 济南: 山东大学, 2016: 16-18.
[8]闫柯, 葛梦然, 高军, 等. 空间锥螺旋管束流体诱导振动换热器及性能分析 [J]. 西安交通大学学报, 2011, 45(11): 22-26.
YAN Ke, GE Mengran, GAO Jun, et al. Performance of flow-induced vibration heat exchanger with conical spiral tube bundle [J]. Journal of Xi’an Jiaotong University, 2011, 45(11): 22-26.
[9]YAN Ke, GE Peiqi, HU Ruirong, et al. Heat transfer and resistance characteristics of conical spiral tube bundle based on field synergy principle [J]. Chinese Journal of Mechanical Engineering, 2012, 25(2): 370-376.
[10] 季家东, 葛培琪, 毕文波. 流体诱导弹性管束振动响应数值分析 [J]. 振动与冲击, 2016, 35(6): 80-84.
JI Jiadong, GE Peiqi, BI Wenbo. Numerical analysis on flow-induced vibration responses of elastic tube bundle [J]. Journal of Vibration and Shock, 2016, 35(6): 80-84.
[11] 季家东, 葛培琪, 毕文波. 换热器内弹性管束流体组合诱导振动响应的数值分析 [J]. 西安交通大学学报, 2015, 49(9): 24-29.
JI Jiadong, GE Peiqi, BI Wenbo. Numerical analysis on combination flow induced vibration responses of elastic tube bundle in heat exchanger [J]. Journal of Xi’an Jiaotong University, 2015, 49(9): 24-29.
[12] 季家东, 葛培琪, 毕文波. 换热器内多排弹性管束壳程流体诱导振动响应的数值分析 [J]. 振动与冲击, 2016, 35(20): 85-89.
JI Jiadong, GE Peiqi, BI Wenbo. Numerical analysis on shell-side flow induced vibration responses of multi-row elastic tube bundles in heat exchanger [J]. Journal of Vibration and Shock, 2016, 35(20): 85-89.
