Time-varying nonlinear dynamics of a deploying piezoelectric laminated composite plate under aerodynamic force

S.F.Lu·W.Zhang·X.J.Song

1 Introduction

In recent years,axially deploying cantilevered composite structures have been used[1,2]for novel variable-span wings of e.g.long-range missiles,extension of robot arms,and other similar applications.Because these types of structure are often used in high-speed operating environments,external disturbance or even their own axial motion can induce large-amplitude vibrations and cause geometrically nonlinear problems that affect both the stability and accurate operation of the structure.The nonlinear dynamic characteristics of the extension process of such cantilever structures remain unknown and would be interesting to analyze.

To conduct theoretical dynamic analysis,such structures are usually modeled as axially extendable cantilever laminated composite beams or plates.The nonlinear dynamic equation that describes their extension is usually a time varying partial differential equation or an ordinary differential equation.Unfortunately,in contrast to steady nonlinear dynamic systems,no systematic solutions of such time varying nonlinear dynamic equations are available at present.Therefore,investigations of this problem usually focus on time-varying dynamic modeling and numerical simulation.An equation for the motion of axially deploying cantilever beams was found by Tabarrok et al.[3]based on Newton’s second law,and the group studied the problem of linear vibration of a cantilever beam during its extension for constant speeds.The small-deformation transverse vibrations of cantilever beams of equal annular cross-section during extension at constant speed in an incompressible fluid were investigated by Taleb and Misra[4].They also analyzed the effects of relevant variables on the dynamic stability of the deploying beam.A flexible robot arm was modeled by Wang and Wei[5]as a removable slender cantilever beam,using Newton’s second law,to investigate its dynamic behavior during extension.An equation of motion for extendable flexible beams was deduced by Behdinan et al.[6]using Hamilton’s principle,and the time-varying dynamical behavior of the axially moving system investigated numerically.The dynamic properties of a deploying cantilever beam were investigated by Deng et al.[7]under various deploying laws using a precision integration method.The exact forced response of a translating string of arbitrarily varying length under constant tension with general initial conditions and external excitation was analyzed by Zhu and Zheng[8].The stability of an axially deploying beam in dense liquids was studied by Gosselin et al.[9],who also deduced the equation of motion for flexible slender cantilever beams with equal annular cross-section during axial extension at constant speed in a dense incompressible fluid.Furthermore,they analyzed the effects of extension speed on the structural stability.The vibration and stability of an axially moving cantilever beam in dense liquids were studied by Wang and Ni[10].The nonlinear dynamic response of axially deploying cantilever beams in supersonic flow was studied by Zhang et al.[11].Variable-span wings were modeled by Huang and Qiu[12]as extendable cantilever beams,and their transient aerodynamic response and fluttering characteristics during a morphing process under aerodynamic force investigated numerically.The linear vibration of an extendable cantilever plate model was studied by Wang et al.[13],who deduced the partial differential equation for its motion and analyzed the variations in frequency and dynamic stability during motion.A nonlinear dynamic equation for axially deploying cantilevered laminated composite plates under combined third-order nonlinear aerodynamic load and in-plane excitation was found by Zhang et al.[14].The group used Reddy’s high-order shear theory,and studied the nonlinear dynamical behavior of the time-varying structure using a numerical approach.The equation governing an axially moving viscoelastic plate was derived by Yang et al.[15]based on Newton’s second law,who also studied the complex natural frequencies for linear free vibrations as well as bifurcation and chaos for forced nonlinear vibrations of the plate using the finite difference method.The natural frequencies of nonlinear planar vibration of axially moving beams were investigated numerically by Ding and Chen[16]using Galerkin methods.Various scholars have studied the dynamical behavior of axially movable cantilever beam structures under external loads using experimental techniques[17–19].The results of the above-mentioned studies show that such axially deploying cantilever structures show complex dynamical behavior under external loads,and that nonlinear dynamic phenomena such as vibration amplitude jumps and divergences can readily occur in the vibration process.Therefore,control of large-amplitude vibration of cantilever structures during their extension remains a great challenge,and it would be highly desirable to improve the design and development of such structures.

Piezoelectric materials are widely used to study vibration suppression for plate–shell structures[20].A piezoelectric laminated composite plate made of piezoelectric material and fiber-reinforced composite benefits from the advantages of the latter,including high specific strength and stiffness and excellent fatigue resistance.Such structures also exhibit improved controllability because the fiber-reinforced composite and piezoelectric materials can be stacked in many ways in the laminated composite plate structure.Studies of the nonlinear dynamics of such piezoelectric laminated composite plates have been carried out for many years.The stretching and bending motions of piezoelectric laminated composite plates were studied by Reddy and Mitchell[21]using two different models.They developed a geometrically nonlinear theory for laminated composite plates with piezoelectric laminates. The nonlinear free and forced vibrations of piezoelectric functionally graded shells under electrothermal and third-order aerodynamic loads were studied by Rafiee et al.[22].The nonlinear dynamic response of a damaged piezoelectric laminated composite plate was investigated by Fu et al.[23]using a finite difference method.A dynamic equation based on high-order shear deformation theory and the von Karman equation wasfound by Huang and Shen[24].They investigated the nonlinear free and forced vibrations of a laminated composite plate with embedded piezoelectric actuators under electrothermomechanical loads using an improved perturbation method.A nonlinear vibration equation for a laminated composite plate with an embedded piezoelectric laminate was deduced by Dash and Singh[25]by applying high-order shear deformation theory.A control equation for piezoelectric functionally graded shells in a thermomagnetic environment was found by Wang et al.[26].The group used Reddy’s high-order shear plate theory and Hamilton’s principle.The one-to-two internal resonance problem of a piezoelectric laminated composite plate under external load was studied by Zhang et al.[27].The dynamic behavior of axial and transverse vibrations of a piezoelectric laminated composite plate was studied numerically by Zhang and Shen[28].Smart control of the vibration of a piezoelectric laminated composite plate was investigated by Wang et al.[29]using first-order shear deformation theory.Active control of the vibration of laminated composite shells containing piezoelectric fiber-reinforced composites was studied by Ray and Reddy[30].Some experimental and theoretical studies on vibration control of piezoelectric laminated composite plate structures were conducted by Qiu et al.[31]and Dong et al.[32]using several methods.In the present work,piezoelectric materials were used in an axially extendable cantilever laminated composite plate structure,and the nonlinear dynamic behavior of the deploying cantilever piezoelectric laminated composite plate,under the combined action of aerodynamic load and piezoelectric excitation,was studied.Using Reddy’s high-order shear deformation theory for laminates and Hamilton’s principle,a partial differential nonlinear model for the dynamics of the deploying cantilever was obtained.Considering the displacement boundary conditions of the structure,a time dependent modal function for structural vibration was found.The ordinary differential form of the time-varying nonlinear dynamic equation for the extendable cantilevered laminated composite plate was obtained by truncating the partial differential form of the nonlinear dynamic equation using the Galerkin method.Then,the effects of variables such as piezoelectric excitation and extension speed on the time-varying nonlinear dynamic stability of the cantilevered piezoelectric laminated composite plate during the extension process were analyzed,considering the characteristic of the piezoelectric material.

2 Equation of motion for deploying piezoelectric laminated composite plate

We consider a model of an axially deploying rectangular cantilevered piezoelectric laminated composite plate formed by bonding a polyvinylidene fluoride(PVDF)piezoelectric membrane with fiber-reinforced composites(Fig.1).Theinitial length of the plate isl0,the width isb,the thickness ish,and the Cartesian coordinate centerOxyis located at the center of the plate.The rectangular cantilever piezoelectric laminated composite plate extends along thex-axis at a time-varying speed with the formV=V0+Vdcos(Ω1t).The external piezoelectric excitation can be described asVe=Vzcos(Ω2t).The structure is also subjected to a transverse aerodynamic load?p;first-order linear piston theory was employed to study the effect of the aerodynamic load on the nonlinear dynamical behavior of the deploying cantilever piezoelectric laminated composite plate.

Based on Reddy’s[33]third-order shear theory for laminates,the displacement field of the laminated composite plate can be described as

whereu0,v0,andw0are the displacements of an arbitrary point on the middle surface inx,y,andzdirections,andφxandφyare angles along they-andx-axis,respectively.

Using von Karman’s geometry theory for the large deformation of a plate,the relationship between the strain displacementεi(i=x x,y y)and curvature displacementγi(i=x y,yz,zx)can be expressed as

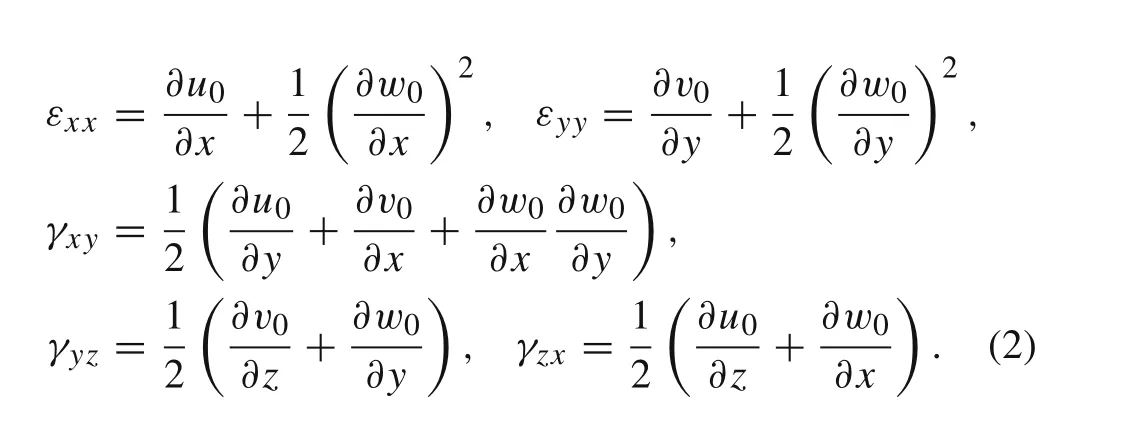
When introducing a piezoelectric laminate into the laminated composite plate,the relationships between the strain displacementεi(i=x x,y y)and curvature displacementγi(i=x y,yz,zx)become

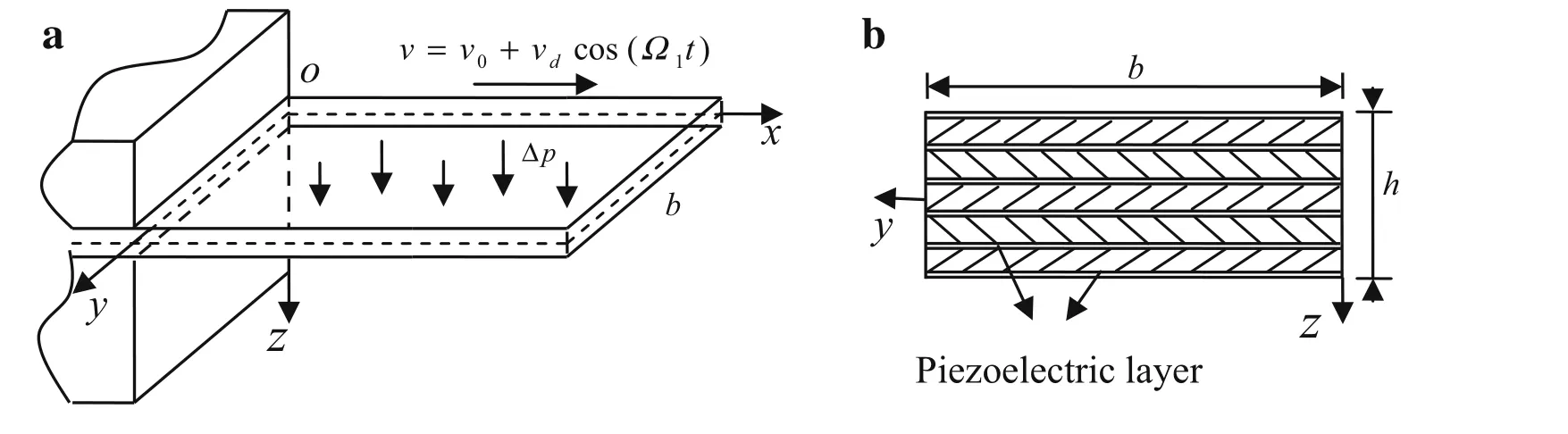
Fig.1 Model of axially deploying piezoelectric cantilever plate

whereeijis the piezoelectric constant andE kis the electric field strength.The stiffness coefficientQ ijcan be expressed as

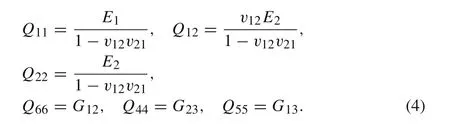
According to Hamilton’s principle,the nonlinear dynamic equation for the deploying cantilevered piezoelectric laminated composite plate can be expressed as

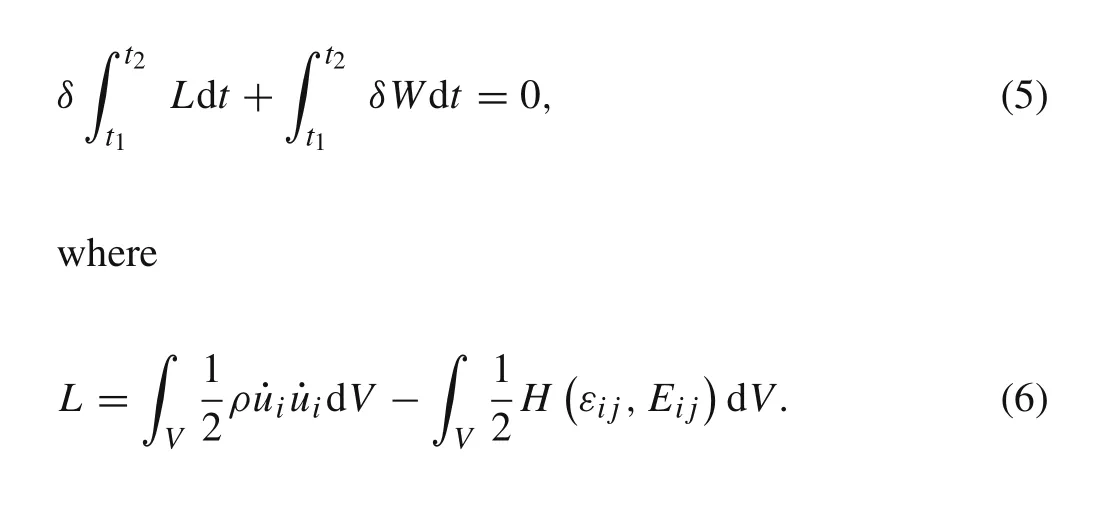
In Eq.(6),the variation of the kinetic energy can be written as

The potential energy of the piezoelectric laminate is

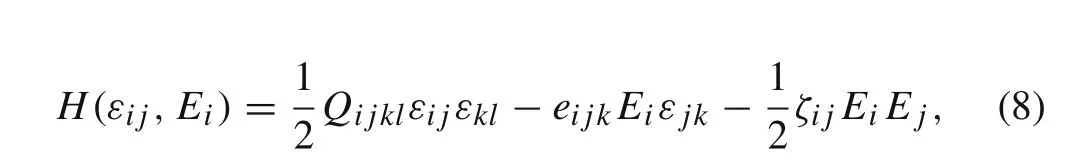
whereQ ijkl,eijk,ζij,andE iare the Young’s modulus,piezoelectric constant,permittivity,and electric field strength,respectively.

The relationship between the electric field strength,electric potential energy,stress,and electric displacement can be described by the following formulas[21]

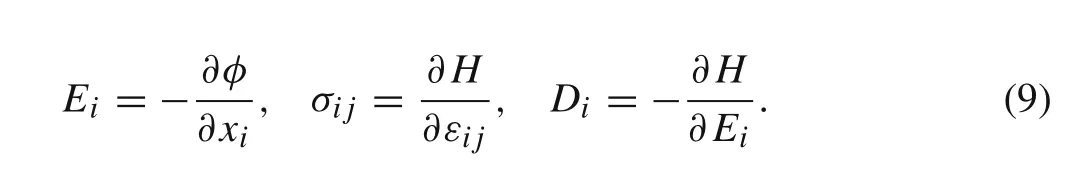
Thus,the variation of the potential energy for a piezoelectric laminated composite plate is

The virtual work of the external force on the system is

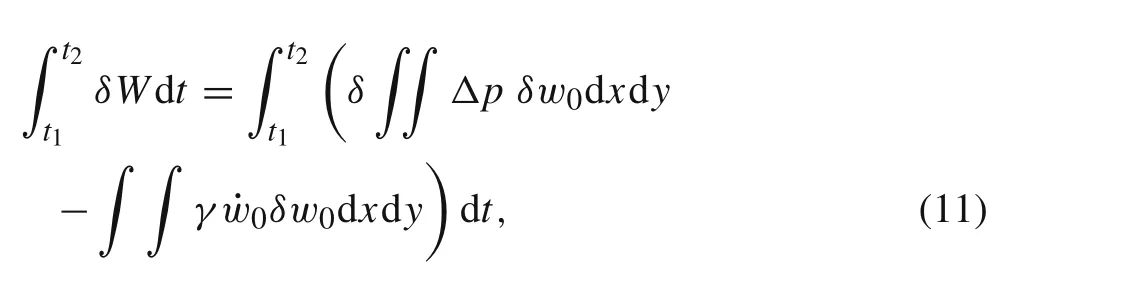
whereγis the structural damping coefficient.

By substituting Eqs.(7),(10),and(11)into Eq.(5)and considering Hamilton’s principle,the nonlinear dynamic equation for the deploying cantilevered piezoelectric laminated composite plate can be obtained as

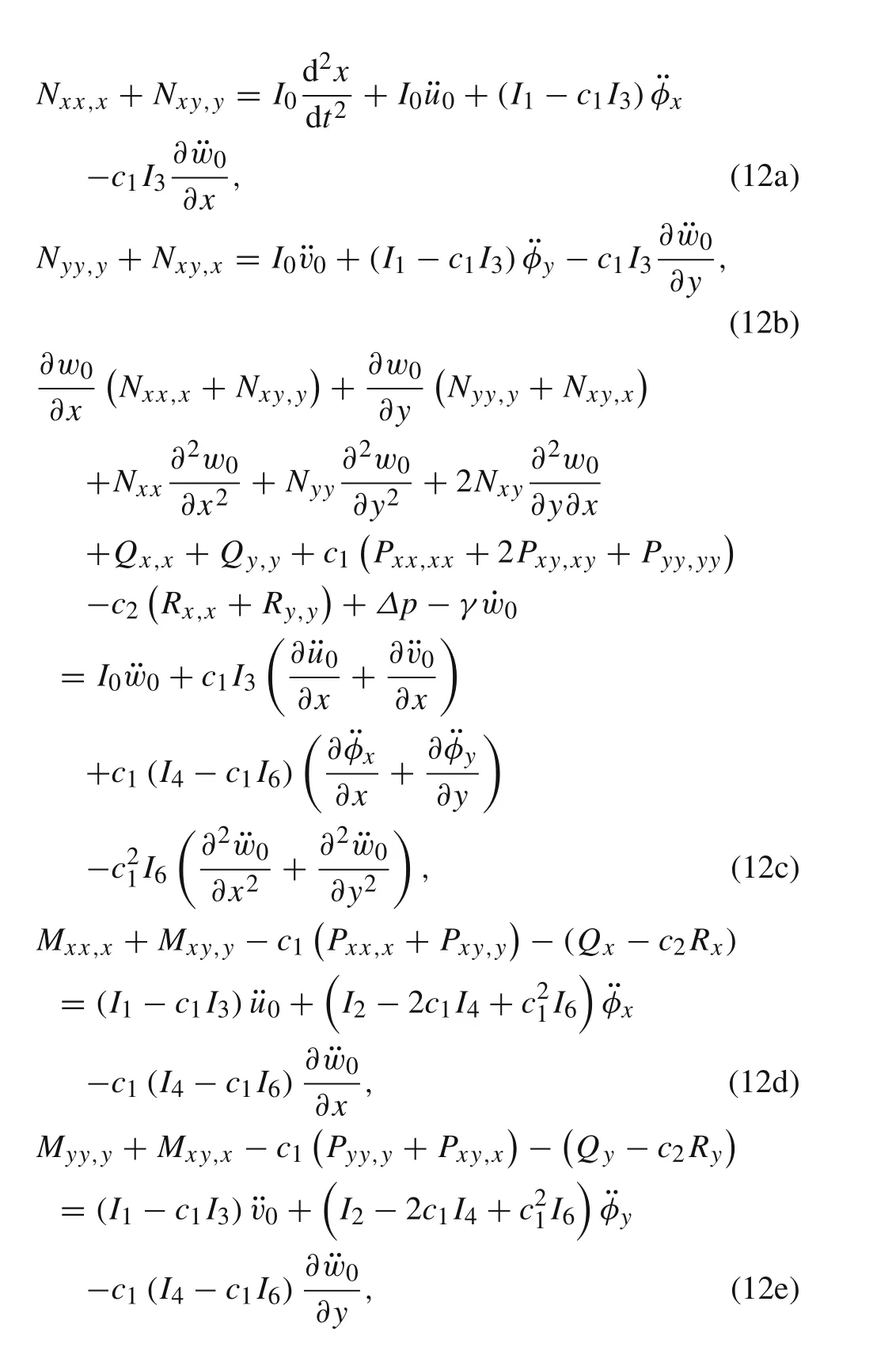
where?pin Eq.(12c)denotes the transverse aerodynamic load obtained by first-order piston theory[34].Since the length of the plate varies with time,the expression for the first-order aerodynamic force applied on the deploying cantilevered plate can be formulated as

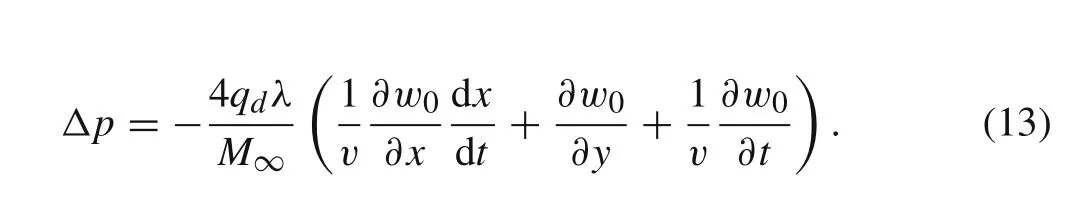
The moment of inertia can be calculated using the following equation

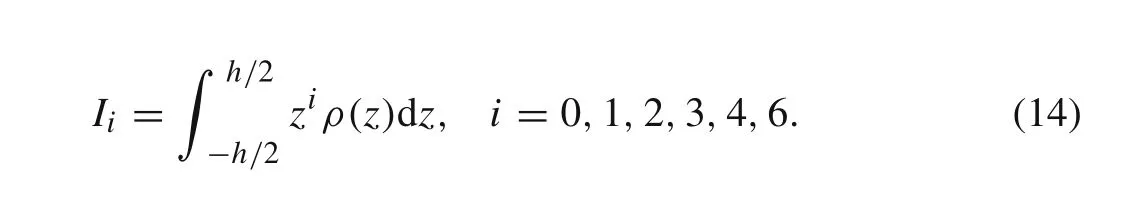
For an orthotropic piezoelectric laminated composite plate,the internal forces can be expressed as

whereeijis the piezoelectric constant,kis the number of the piezoelectric laminate,andE zis the electric field strength.The relationship between the electric field strength and applied voltageVeisE z=Ve/h z,whereh zis the thickness of the piezoelectric laminate.

Inserting Eqs.(15)and(16)into Eq.(12),the nonlinear dynamic equation for the deploying cantilever piezoelectric laminated composite plate,expressed in terms of generalized displacement variables,can be obtained as

3 Galerkin discretization

Due to the difficulty in finding an analytical solution to these partial differential equations describing the vibration of the system,they are usually discretized into equations of ordinary differential form for analysis.Moreover,as lower frequency vibrations are dominant in nonlinear vibration systems,truncation at the first two modes is accurate enough in this case.In this work,the Galerkin method was employed to perform second-order truncation of the nonlinear dynamics in Eq.(17)in partial differential form,selecting the following time-dependent modal function satisfying the displacement boundary conditions

whereX i(x)is the clamped–free beam function along thexaxis,Y j(y)is the free–free beam function along they-axis,andkiandk jare roots of the characteristic equation with the following relationship

wherelis an abbreviation forl(t).

Considering the effect of the change in the length of the plate along thex-axis as time varies,in the process of substituting the vibration mode function into the relevant equations to perform the Galerkin discretization,the accompanying compound derivative argument should be considered.Therefore,the following relational expressions are used for the derivation

Substituting the modal function Eq.(18)into Eq.(17),the Galerkin method is employed to perform the second-order discretization to obtain normalized ordinary differential equations.Because the main structural vibration is out of plane,u0,v0,φx,andφyare expressed using the transverse variablesw1andw2.The dimensionless two-degree of freedom(DOF)nonlinear dynamic equations describing the transverse vibration of the deploying cantilever piezoelectric laminated composite plate can then be formulated as

where the coefficientsαiandβi(i=1,2,...,10)consider timetexplicitly.

4 Numerical simulations

We selected as a model a deploying symmetric cross-ply piezoelectric laminated composite cantilever plate with the following parameters,constructed from PVDF membrane and fiber-reinforced laminates:l0=2.0 m,b=1.5 m,h=0.004 m,f0=2000 N/m2,Vd=0.005 m/s,Ω1=15,Ma=3.0 in hypersonic flow,Va=900 m/s,κ=1.4,and air densityρa=0.65 kg/m3at height of 10,000 m.The material properties of the fiber-reinforced composite composed of graphite–epoxy HT3/QY8911 include:E1=125.0 GPa,E2=7.2 GPa,G12=G13=4.1 GPa,G23=1.43 GPa,ν12=0.33,ν21=ν12E2/E1,ρ=1570 kg/m3,γ=350 N·s/m,with thickness of the piezoelectric layerh z=0.00015 m.Based on the time-varying two-DOF nonlinear dynamic Eq.(23),the nonlinear dynamical behavior of the cantilever piezoelectric laminated composite plate, extending from 2 to 4 m at various extending speeds under first-order aerodynamic force,was investigated numerically.

4.1 Nonlinear dynamical behavior of plate for extension speed V0=0.05

Figures 2–7 show the time history curves for the transverse first-and second-order modal vibration of the cantilever piezoelectric laminated composite plate during the extension process for different piezoelectric excitations.For better observation of the second-order vibration of the structure,the seemingly stable parts in sub figure b are magnified and shown in subfigure c.The effects of the applied voltage on the stability of the time-varying nonlinear dynamics can be observed in the time-domain plots.

The obtained time history curves well reflect the effects of changing the applied voltage on the stability of the time varying nonlinear dynamics.For applied voltage of0(Fig.2),the structural nonlinear dynamic behavior is consistent with that of the fiber-reinforced laminated composite plate without piezoelectric laminates,consistent with Ref.[14].More specifically,during the extension process to 2 m length,three different phases present either the first-or second-order vibration of the structure,including two jumps of vibration amplitude and a stable motion phase between them.Throughout the process,the vibration amplitude of the structure changes greatly,and the structure easily becomes unstable and divergent.For excitation voltage ofVz=130 V(Fig.3),the period of the two jumps in vibration amplitude increases,while the period of stable motion between them decreases.As the excitation voltage increases(Fig.4),the stable motion phase in both the first-and second-order vibrations of the structure gradually decreases and eventually vanishes.Hence,the nonlinear dynamical behavior is very unstable,as the structure experiences a second jump in vibration amplitude immediately after the first one.

On changing the polarity of the excitation voltage,we observe a change in the structural dynamical behavior.When the excitation voltage isVz=−40 V(Fig.5),it is found that the increasing trend in amplitude is slowed in both the first and second-order vibration.When the excitation voltage is increased toVz=−45 V(Fig.6)and the dimensionless time is aroundt=250,the first-and second-order jumps of the vibration amplitude are suppressed.On further increasing the excitation voltage toVz=−50 V(Fig.7),the cantilevered piezoelectric laminated composite plate accomplishes the extension from 2 to 4 m without a second vibration amplitude jump in the first-or second-order vibration.

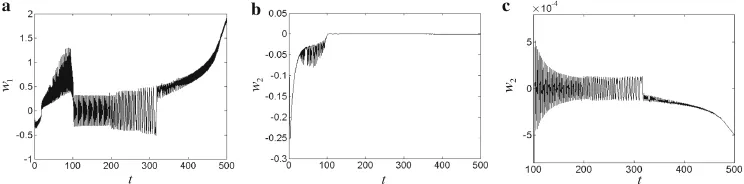
Fig.2 Time history curves for Vz=0 V

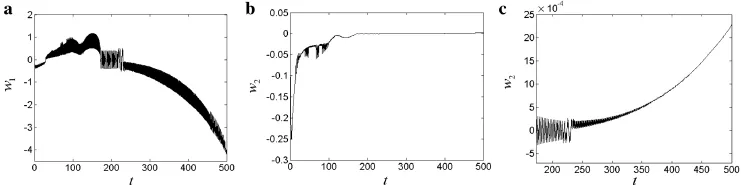
Fig.3 Time history curves for Vz=130 V

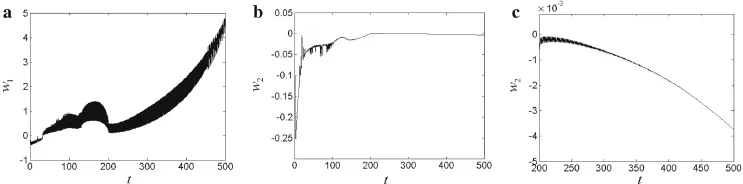
Fig.4 Time history curves for Vz=150 V

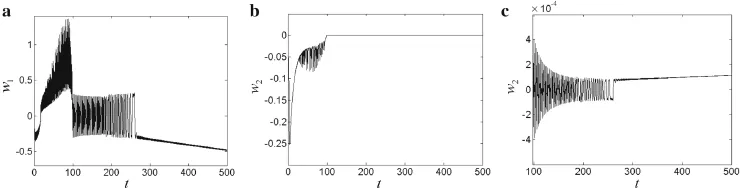
Fig.5 Time history curves for Vz=−40 V

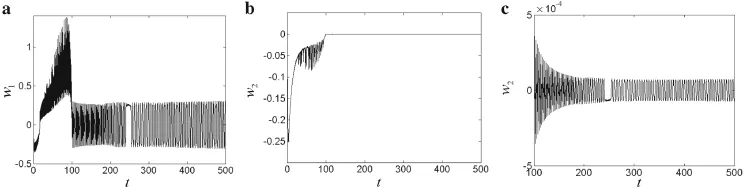
Fig.6 Time history curves for Vz=−45 V

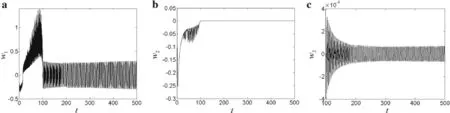
Fig.7 Time history curves for Vz=−50 V

Overall,the piezoelectric excitation has a significant impact on the stability of the structural nonlinear vibration.During the extension of the cantilever piezoelectric laminated composite plate from 2 to 4 m,when the excitation voltage is positive,the structural stability of the first and second-order vibrations gradually decreases.The stable motion phase of the system gradually shrinks in time,and the structure is liable to exhibit a second jump immediately after the first jump of the vibration amplitude.When the voltage is increased further,the vibration of the structure gradually deviates from the equilibrium position until the structure eventually diverges.On changing the polarity of the voltage,as the voltage increases in the negative direction,even though the first jump of the first two vibration amplitudes is not suppressed,the second jump in the first-and second-order vibrations is avoided.As a result,the scale of the vibration amplitude in the stable motion phase is reduced.By calculating the coefficients of the in-plane stiffness terms in Eq.(23),we note that the in-plane stiffness of the plate was improved with increase of the applied negative voltage.This increase of the in-plane stiffness leads to a corresponding increase of the structural vibration frequency,which explains why the nonlinear vibration amplitude was suppressed.

4.2 Nonlinear dynamic behavior of plate for extension speed of V0=0.10

To study the effects of changing the extension speed on the structural stability of the nonlinear dynamics,the time history response curves of the deploying cantilever piezoelectric laminate,extending from 2 to 4 m at extension speed ofV0=0.10 m/s,are shown in Figs.8–11.When the amplitude of the excitation voltage is increased from 0 to 150 V,the time-varying first-and second-order nonlinear vibrations gradually lose their stability,and the instability of the extension process is exacerbated.On gradually adjusting the negative excitation voltage,it was found that,when the excitation voltage wasVz=−150 V,the second jump of the structural vibration amplitude in the first-and second order vibrations was avoided.However,the first jump was not suppressed,although the scale of the vibration amplitude in the stable motion phase was suppressed.At the same time,the vibration amplitude during the stable motion phase was suppressed.In other words,choice of an appropriate excitation voltage can effectively suppress the nonlinear vibration of the system during the extension process.In addition,on comparison with Sect.4.1,it is found that the stability of the system gradually decreased during the extension process as the extension speed was increased.When the structure extended at higher speed,the negative applied voltage necessary to avoid the second jump of the amplitude of the first-and second-order structural vibrations also increased correspondingly.

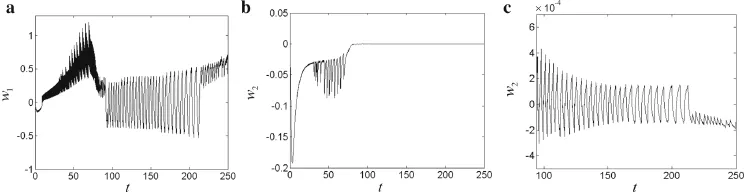
Fig.8 Time history curves for Vz=0 V

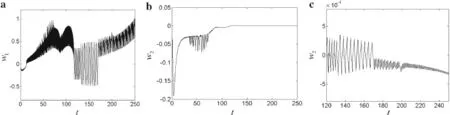
Fig.9 Time history curves for Vz=100 V

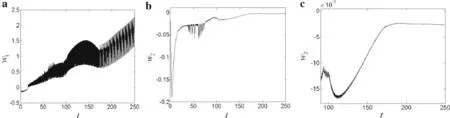
Fig.10 Time history curves for Vz=150 V

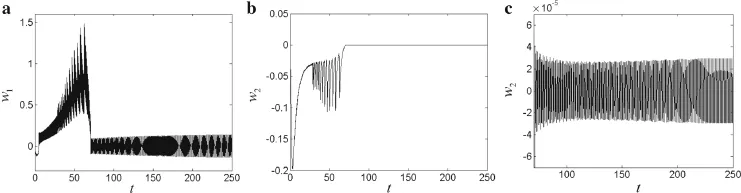
Fig.11 Time history curves for Vz=−150 V

5 Conclusions

Considering the piezoelectric material characteristics,the time-varying nonlinear dynamic behavior of a deploying laminated composite plate,under the combined action of first-order aerodynamic load and piezoelectric excitation,was investigated.The effect of the introduction of the piezoelectric material on the stability of the nonlinear dynamics of the composite piezoelectric laminate during the extension process was investigated numerically.The following conclusions can be drawn:

(1)Using Reddy’s third-order shear theory for laminates and von Karman’s geometric relation for large deformation,and applying Hamilton’sprinciple,a nonlinear dynamic model in partial differential form for the deploying laminated composite plate,considering the combined action of aerodynamic load and piezoelectric excitation,was developed.Based on a selected time-dependent modal function,we performed second-order discretization using the Galerkin method,resulting in the derivation of a time-varying nonlinear dynamic model describing the transverse vibration of the deploying cantilever piezoelectric laminated composite plate.

(2)Using the obtained ordinary differential equation,the time-varying nonlinear dynamic behavior of the deploying cantilever piezoelectric laminated composite plate was simulated numerically,and the effect of the piezoelectric effect on the time-varying nonlinear dynamical behavior discussed.The results reveal that,when the applied voltage is positive,the extension process becomes more unstable,and the time varying structural divergence is exacerbated.As a result,the piezoelectric laminated composite plate is more liable to failure and destruction.When the applied voltage was set to a negative value,the polarity of the voltage changed,and it was found that not only was the increasing trend of the vibration amplitude of the time-varying structure suppressed,but also the vibration amplitude was suppressed.Thus,the piezoelectric material has a significant impact on the nonlinear dynamic stability of the fiber-reinforced laminated composite plate,and choice of a suitable voltage and polarity can effectively suppress the nonlinear vibration of the deploying cantilever laminate.The applied negative voltage enhances the in-plane stiffness of the time-varying structure,which leads to a corresponding increase of the structural vibration frequency and suppression of the nonlinear vibration amplitude.It is also found that increasing the extension speed can decrease the nonlinear dynamic stability of the structure during the extension process.Therefore,the applied excitation voltage required to suppress the divergence of the nonlin-ear vibration amplitude should be increased correspondingly when the structure extends at higher speed.

AcknowledgementsThe project was supported by the National Natural Science Foundation of China(Grants 11402126,11502122,and 11290152)and the Scientific Research Foundation of the Inner Mongolia University of Technology(Grant ZD201410).

1.Lee,B.H.K.,Price,S.J.,Wong,Y.S.:Nonlinear aeroelastic analysis of airfoil:bifurcation and chaos.Prog.Aerospace Sci.35,205–334(1999)

2.Arrison,M.,Birocco,K.,Gaylord,C.,et al.:2002–2003 AE/ME morphing wing design.Virginia Tech Aerospace Engineering Senior Design Project Spring Semester Final Report.(2003)

3.Tabarrok,B.,Leech,C.M.,Kim,Y.I.:On the dynamics of an axially moving beam.J.Frankl.Inst.297,201–220(1974)

4.Taleb,I.A.,Misra,A.K.:Dynamics of an axially moving beam submerged in a fluid.J.Hydronaut.15,62–66(1981)

5.Wang,P.K.C.,Wei,J.D.:Vibration in a moving flexible robot arm.J.Sound Vib.116,149–160(1987)

6.Behdinan,K.,Stylianou,M.,Tabarrok,B.:Dynamics of flexible sliding beams non-linear analysis.Part I:formulation.J.Sound Vib.208,517–539(1997)

7.Deng,Z.C.,Zheng,H.J.,Zhao,Y.L.,et al.:On computation of dynamic properties for deploying cantilever beam based on precision integration method.J.Astronaut.22,110–113(2001).(in Chinese)

8.Zhu,W.D.,Zheng,N.A.:Exact response of a translating string with arbitrarily varying length under general excitation.J.Appl.Mech.75,519–525(2008)

9.Gosselin,F.,Paidoussis,M.P.,Misra,A.K.:Stability of a deploying/deploying beam in dense fluid.J.Sound Vib.299,124–142(2007)

10.Wang,L.,Ni,Q.:Vibration and stability of an axially moving beam immersed in fluid.Int.J.Solids Struct.45,1445–1457(2008)

11.Zhang,W.,Sun,L.,Yang,X.D.,etal.:Nonlinear dynamic behaviors of a deploying-and-retreating wing with varying velocity.J.Sound Vib.332,6785–6797(2013)

12.Huang,R.,Qiu,Z.P.:Transient aeroelastic responses and flutter analysis of a variable-span wing during the morphing process.Chin.J.Aeronaut.26,1430–1438(2013)

13.Wang,L.H.,Hu,Z.D.,Zhong,Z.:Dynamic analysis of an axially translating plate with time-variant length.Acta Mech.215,9–23(2010)

14.Zhang,W.,Lu,S.F.,Yang,X.D.:Analysis on nonlinear dynamics of a deploying cantilever laminated composite plate.Nonlinear Dyn.76,69–93(2014)

15.Yang,X.D.,Zhang,W.,Chen,L.Q.,et al.:Dynamical analysis of axially moving plate by finite difference method.Nonlinear Dyn.67,997–1006(2012)

16.Ding,H.,Chen,L.Q.:Nonlinear dynamics of axially accelerating viscoelatic beams based on differential quadrature.Acta Mechanica Solida Sinica 22,267–275(2009)

17.Matsuzaki,Y.,Torii,H.,Toyama,M.:Vibration of a cantilevered beam during deployment and retrieval:analysis and experiment.Smart Mater.Struct.4,334–339(1995)

18.Liu,K.F.,Deng,L.Y.:Experimental verification of an algorithm for identification of linear time-varying systems.J.Sound Vib.279,1170–1180(2005)

19.Liu,K.F.,Deng,L.Y.:Identification of pseudo-natural frequencies of an axially moving cantilever beam using a subspace-based algorithm.Mech.Syst.Signal Process.20,94–113(2006)

20.Fuller,C.R.,Elliott,S.J.,Nelson,P.A.:Active Control of Vibration.Academic Press,San Diego(1996)

21.Reddy,J.N.,Mitchell,J.A.:On refined nonlinear theories of laminated composite structures with piezoelectric laminae.Sadhana 20,721–747(1995)

22.Rafiee,M.,Mohammadi,M.,Sobhani Aragh,B.,et al.:Nonlinear free and forced thermo-electro-aero-elastic vibration and dynamic response of piezoelectric functionally graded laminated composite shells,PartI:Theory and analytical solutions.Compos.Struct.103,179–187(2013)

23.Fu,Y.M.,Wang,X.Q.,Yang,J.H.:Nonlinear dynamic response of piezoelastic laminated plates considering damage effects.Compos.Struct.81,353–361(2007)

24.Huang,X.L.,Shen,H.S.:Nonlinear free and forced vibration of simply supported shear deformable laminated plates with piezoelectric actuators.Int.J.Mech.Sci.47,187–208(2005)

25.Dash,P.,Singh,B.N.:Nonlinear free vibration of piezoelectric laminated composite plate.Finite Elem.Anal.Des.45,686–694(2009)

26.Wang,Y.,Hao,Y.X.,Wang,J.H.:Nonlinear vibration of a cantilever FGM Rectangular plate with piezoelectric layers based on thirdorder plate theory.Adv.Mater.Res.415–417,2151–2155(2012)

27.Zhang,W.,Yao,Z.G.,Yao,M.H.:Periodic and chaotic dynamics of laminated composite plated piezoelectric rectangular plate with one-to-two internal resonance.Sci.China Ser.E Technol.Sci.52,731–742(2009)

28.Zhang,H.Y.,Shen,Y.P.:Vibration suppression of laminated plates with 1–3 piezoelectric fiber-reinforced composite layers equipped with interdigitated electrodes.Compos.Struct.79,220–228(2007)

29.Wang,S.Y.,Quek,S.T.,Ang,K.K.:Vibration control of smart piezoelectric composite plates.Smart Mater.Struct.10,637–644(2001)

30.Ray,M.C.,Reddy,J.N.:Active control of laminated cylindrical shells using piezoelectric fiber reinforced composites.Compos.Sci.Technol.65,1226–1236(2005)

31.Qiu,Z.C.,Zhang,X.M.,Wu,H.X.,et al.:Optimal placement and active vibration control for piezoelectric smart flexible cantilever plate.J.Sound Vib.301,521–543(2007)

32.Dong,X.J.,Meng,G.,Peng,J.C.:Vibration control of piezoelectric smart structures based on system identification technique:Numerical simulation and experimental study.J.Sound Vib.297,680–693(2006)

33.Reddy,J.N.:Mechanics of Laminated Composite Plates and Shells:Theory and Analysis.CRC Press LLC,Boca Raton(2004)

34.Ashley,H.,Zartarian,G.:Piston theory-a new aerodynamic tool for the aeroelastician.J.Aeronaut.Sci.23,1109–1118(1956)