Measurement of the flow structures in the wakes of different types of parachute canopies

Sylvio Pasqualini·Zheyan Jin·Zhigang Yang

1 Introduction

As a type of aerodynamic decelerator,parachutes have been widely used in life-saving and recovery systems.Based on their geometries,parachutes can be classified into round parachutes,cross-type parachutes,and ribbon parachutes.Because most parachutes use fabric canopies,the fabric flexibility results in apparent changes in the canopy geometry during both inflation and terminal descent phases[1].Moreover,because of the fabric permeability,small air flow can go through the canopy surface.The unsteady flow in the wake,together with the flexible fabric canopy,leads to unavoidable fluid–structure interaction[2].Further insight into the flow fields in the wakes of the flexible canopies not only allows us to have a better understanding of the unsteady aerodynamics pertinent to the parachutes,but offers important knowledge for scientists to develop superior parachutes as well[3].

Through the years,scientists have carried out extensive investigations into the aerodynamic characteristics of different types of parachutes[4–16].For example,Peterson et al.[7]reported a review on the characteristics of parachute canopies from deployment phase to terminal descent phase.Furthermore,Levin and Shpund[8]changed the geometry of the cross parachute canopies to optimize their aerodynamic performance.In their work,Stein et al.[9]numerically investigated the interactions between two approaching parachute canopies in a cluster of parachutes.Also,Yagiz et al.[10]reported the influence of the geometry of three parachute canopies on the tangential force coefficient.In their work,Johari and Levshin[11]studied the interaction of a line vortex aligned with the axis of fully inflated parachute canopies.Then,Han et al.[12]proposed multi-node models to calculate the shape of full-filled cross parachutes.The study by Xue et al.[13]numerically investigated the effects of suspension lines on the flow field around a rigid supersonic parachute mode.In addition,Xue et al.[14]performed 3-D simulations to investigate the supersonic flow over rigid parachute models and focused on the effects of the trailing distances and the ratio of the diameter of capsule to canopy.The work of Gao et al.[15]presented the fluid–structure interaction(FSI)phenomenon of a parachute during finite mass inflation with low speed and altitude.Moreover,Gao et al.[16]performed the inflation simulations of a full-scale model disk-gapband parachute from the Mars Science Laboratory(MSL)mission.

Fig.1 Configuration of the parachute models.a Ribbon.b 8-branches.c Cross

Fig.2 The parachute model and forebody support structure in the wind tunnel

Fig.4 Illustrations of the laser sheet arrangement behind the cross parachute canopy.a Position A.b Position B

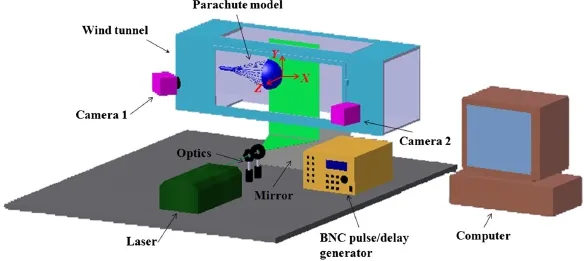
Fig.3 Experimental setup

Recently,some researchers have used particle image velocimetry(PIV)to carry out the flow field measurements on several types of parachute models.For example,Desabrais[17]investigated the flow field in the wake of a flexible generic round parachute canopy.Also,Wernet et al.[18]obtained the velocity distributions of the shock locations during the canopy shock oscillations on a rigid supersonic parachute model.In their work,Schairer et al.[19]conducted unsteady flow measurements in the wake of a tension-cone decelerator in the subsonic flow.The study by Sengupta et al.[20]measured the velocity field upstream of the Orion drogue parachute model.More recently,by using stereoscopic particle image velocimetry(stereo-PIV),Jin et al.[21]studied the effect of Reynolds number on flow structures in the wake of a circular parachute canopy.In addition,Jin et al.[22]also investigated the influence of the arm ratio of the cross canopy on the wake structures in terms of velocity,vorticity,and Reynolds stress.

Although much research has been performed on different parachute models in the past[1–22],the quantitative measurements to reveal the flow structures in the wakes of the parachute canopies with different geometries,but the same surface area have not yet been investigated.Since parachutes can be classified into different types based on their geometries,it would be interesting to know the effects of the geometry of the flexible parachute canopies on the flow structures in their wakes.In this study,an experimental investigation was carried out to characterize the flow structures in the wakes of three different parachute canopies by using stereo-PIV technique.All these three parachute canopies had the same surface area.The objective of this study is to further our understanding of the unsteady aerodynamics related to the flexible parachute canopies.

Fig.5 Instantaneous vorticity results when Re=33,314.a Ribbon.b 8-branches.c Cross(position A).d Cross(position B)

2 Experimental

2.1 Parachute models

Three parachute models were made of the solid cloth of a used personnel parachute(Fig.1).These models had the same surface area(S=0.015 m2)and were named ribbon canopy,8-branches canopy,and cross canopy,respectively.The constructed length,the thickness,and the cloth density of these canopies was 150.0 mm,0.1 mm,and 34.92 g·m−2,respectively.The arm ratio(i.e.,AR=L/W,whereLis the length andWis the width)of the cross canopy was measured to be 2.10.

Figure 2 shows the inflated canopy and the supporting mount at the test section of the wind tunnel.Nylon suspension lines were used to attach the canopy to a fore body.The number of nylon suspension lines for ribbon canopy,8-branches canopy,and cross canopy was 28,24,20,respectively.The detailed information of fore body,suspension lines,stainless steel rods,and retention line has been given in our previous studies[21,22].

2.2 Experimental setup

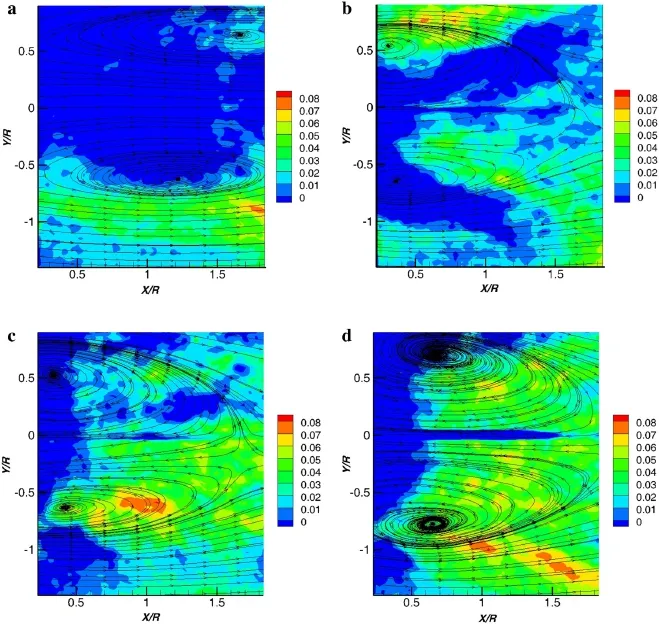
Fig.6 Streamlines and the ensemble-averaged normalized z-component of the velocity(Uz/U∞)with Re=33,314.a Ribbon.b 8-branches.c Cross(position A).d Cross(position B)

The present experimental investigation was performed in a low speed wind tunnel.During the experiments,the speed of the incoming airflow,U∞,changed from 3.36 to 7.50 m·s−1.By using the constructed length of the canopy as the characteristic length,the Reynolds numbers varied in the range 33,314?R e?74,362.The current experimental setup is shown in Fig.3,which has been described in our previous study[21,22].It should be noted that the angle displacement arrangement with the Scheimpflug condition was used in the present stereo-PIV measurements.In addition,in the images obtained by the charge coupled device(CCD)cameras,each pixel represented an actual distance of 0.095 mm.The interested readers are referred to Refs.[21,22]for details.

3 Results and discussions

In this study,the room temperature was kept at(21.5±0.5)°C,while the relative humidity of the surrounding air was held at(62.0±2.0)%.In order to avoid the laser lights reflected by the parachute canopies,we did not record the flow field information immediately downstream of the parachute canopies.In addition,as shown in Fig.3,the apex of the parachute was chosen to be the origin of the coordinate system.A parameter,R,was defined as the constructed radius,which was half of the constructed length(L).The region of interest was selected at a region where 0.22R?x?1.85Rand−1.4R?y?0.9R.Figure4 illustrates the laser sheet arrangement behind the cross parachute canopy.Position A represents the flow over arm and position B represents the flow through gap.For each case,the image acquisition rate of the stereo-PIV measurement was chosen at 4.0 Hz and it was different from the frequency of the “breathing”phenomenon of the parachute canopies.In addition,a sequence of 350 stereo-PIV images was captured for each case.

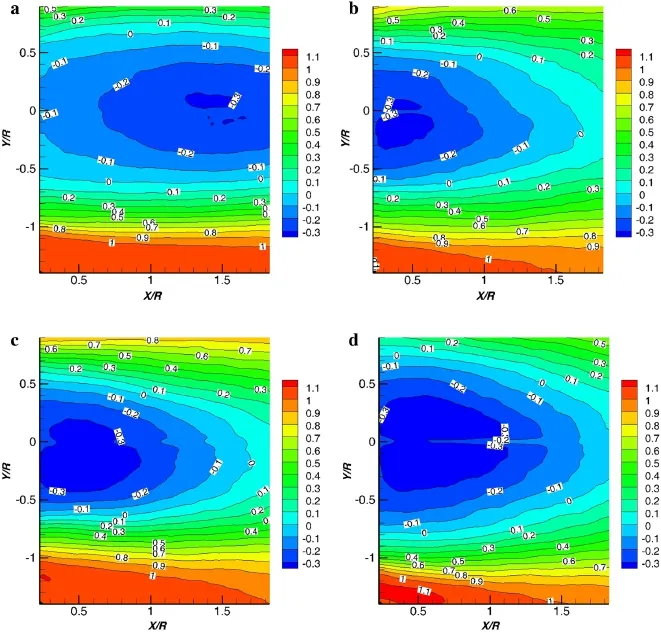
Fig.7 Ensemble-averaged normalized x-component of the velocity(Ux/U∞)with Re=33,314.a Ribbon.b 8-branches.c Cross(position A).d Cross(position B)

By following the procedures of the previous studies[21,22],the normalized Reynolds stress(¯τ)and turbulence kinetic energy(TKE)were defined,the uncertainties of,which were about 5%.In addition,the time-averaged projected areas of these parachute canopies were obtained to be less than 105.0 cm2,which meant that the blockage ratios were less than 4.2%.

Figure 5 shows the instantaneous vorticity distributions in the wakes of different types of parachute canopies at Reynolds number of 33,314.For all the canopies,vortices of different intensities appeared in their wakes.However,the vortices in the ribbon canopy case were found to have less vorticity than those of the other cases.Such a phenomenon might be because of the many small orifices distributed on the surface of the ribbon canopy.When air flow penetrates the ribbon canopy,they create many small-scale jet flows,which induce vortices with relatively lower intensity.Similar to the observation in Ref.[6],for the cross canopy,a larger turbulent wake was found in the flow through gap(position B)in comparison with the flow over arm(position A).In our results,concentrated vorticity regions could be found near thex-axis,which were because of the existence of retention line and should be neglected.

Figure 6 shows the streamlines and ensemble-averaged normalizedz-component of the velocity(Uz/U∞)distributions in the wakes of these three parachute canopies at Reynolds number of 33,314.For all cases,a recirculation zone formed in the wake,which was similar to that of the circular parachute canopy case[21].However,the recirculation zone in the wake of the ribbon canopy seemed to be totally different from those of the other cases.It occurred at a further downstream region than the others.In addition,the recirculation zone of the flow over the arm of the cross canopy(position A)was smaller than that of the flow through the gap(position B).Moreover,the distributions of thez-component of the velocity of the ribbon canopy were also dramatically different from those of the other cases.Because of the influence of the gravity of the canopies,the retention line might not hold the parachute canopies perfectly horizontal,which could result in the asymmetry of the recirculation zones in the wakes of these parachute canopies.

Fig.8 The transverse profiles of ensemble-averaged normalized x-component of the velocity with x=1.5 R.a Ribbon.b 8-branches.c Cross(position A).d Cross(position B)

The ensemble-averaged normalizedx-component of the velocity results(Ux/U∞)in the wakes of different kinds of parachute canopies at Reynolds number of33,314 are shown in Fig.7.In order to better explain the results,Z Ux=0was used to represent the velocity zone confined byUx/U∞=0.Generally speaking,three features can be observed from these results.Firstly,the center of the velocity zoneZ Ux=0of the ribbon canopy located further downstream than those of the other cases.Secondly,as for the cross canopy,the size of the velocity zoneZ Ux=0of the flow through gap(position B)was much larger than that of the flow over arm(position A).Thirdly,the size of the velocity zoneZ Ux=0of the flow at either position A or position B of the cross parachute in the present study was smaller than that of the circular parachute tested by Jin et al.[21].The possible reason for such a phenomenon might be due to that the cross shape allowed the airflow to move around more easily than the circular shape.

In the present study,the transverse profiles of the variables in the wakes of different kinds of parachute canopies at different Reynolds numbers were also obtained and analyzed.For example,at location wherex= 1.5R,the transverse profiles ofx-component of the velocity are shown in Fig.8.The results indicated that the effect of the Reynolds number on the transverse profiles of thex-component of the velocity was insignificant for all these canopies.In addition,the minimum values of thex-component of the velocity for the ribbon canopy case were generally lower than those of the other canopies.In addition,the transverse profiles were not symmetrical with respect to thex-axis,which corresponded to the results in Figs.6 and 7.

Fig.9 Ensemble-averaged normalized vorticity(ωz L/U∞)with Re=33,314.a Ribbon.b 8-branches.c Cross(position A).d Cross(position B)

Figure 9 shows the ensemble-averaged normalized vorticity distributions(ωz L/U∞)in the wakes of these parachute canopies at a Reynolds number of 33,314.For all cases,the majority of the vorticity appeared near the area wherey≈ −1.0Rand decayed rapidly.As for the cross canopy,the concentrated vorticity region at position A was located closer to thex-axis when compared to that at position B.Near thex-axis,two parallel concentrated vorticity regions appeared,which were induced by the existence of retention line and should be neglected.However,the error induced by the existence of retention line was more obvious at position B(Fig.9d)than that at position A(Fig.9c).The possible explanation for this phenomenon might be that the combination of the unsteady wake flow and the flexible canopy produced unavoidable fluid–structure interaction between the canopy and the airflow.Since the canopy was restricted by the retention line,the strong interaction between the canopy and the airflow certainly induced the retention line to move.When the canopy was placed at different positions,the fluid–structure interaction between the canopy and the airflow was different,which might induce the retention line to move in a different way.Since our stereo-PIV setup could only measure a fixed vertical region,the movement of the retention line in that region might be different,which led to the different results at the location wherey≈0.

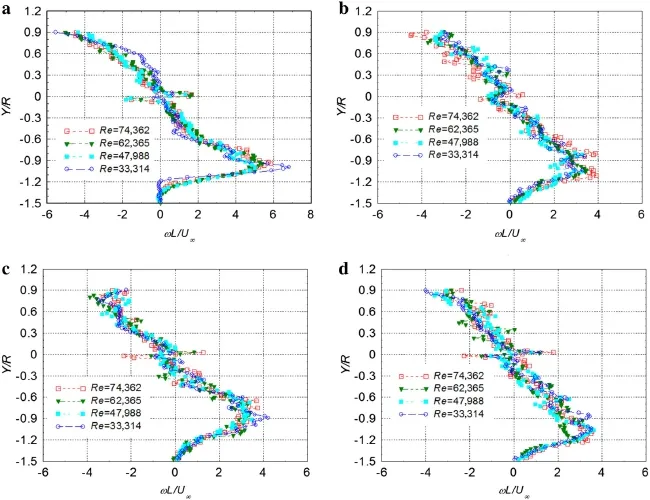
Fig.10 The transverse profiles of ensemble-averaged normalized vorticity where x=1.5 R.a Ribbon.b 8-branches.c Cross(position A).d Cross(position B)

Figure 10 shows transverse profiles of ensemble-averaged normalized vorticity at different Reynolds numbers.For all cases,a vorticity protrusion was present near the region withy≈ −1.0R,which was corresponded to the vorticity concentrated region in Fig.9.When the Reynolds number increases,the ensemble-averaged normalized vorticity distributions change minor.Large fluctuations appear in the normalized vorticity in the area withy≈0,due to the retention line.This should be neglected.Moreover,for all these cases,at the region wherey≈ −1.4R,the ensemble-averaged normalized vorticity values reduced approximately to 0.It should be noted that the fluctuations appeared in the transverse profiles of the vorticity.This phenomenon might be explained by two factors.Firstly,when Johari and Desabrais[1]studied the vortex shedding in the near wake of a circular parachute canopy,their mean vorticity field was obtained by averaging 1000 instantaneous fields.However,their vorticity results also presented a fluctuated feature.Thus,we think that the highly turbulent and unsteady characteristics of the wake of the canopy might play an important role.Secondly,the geometric difference between the different canopies in the present study and the round canopy[1]might be a reason,which led to a more turbulent flow.

The normalized Reynolds stress distributions in the wakes of these three canopies at a Reynolds number of 33,314 are shown in Fig.11.As can be seen,the Reynolds stress levels of the ribbon canopy were much lower than those of the other canopies.As for the cross canopy,at position A,the majority of the Reynolds stress appeared within the area where−1.0R?y?1.0Rand decayed rapidly.At position B,the regions with concentrated Reynolds stress were further extended to the locations where|y|＞1.0R.Lower values of the Reynolds stress were found at position B,compared to position A.It should be noted that the Reynolds stress distribution of the 8-branches canopy was similar to that of the cross canopy at position A.

Fig.11 Normalized Reynolds stress distributions when Re=33,314.a Ribbon.b 8-branches.c Cross(position A).d Cross(position B)

The transverse profiles of normalized Reynolds stress in the wakes of the parachute canopies are shown in Fig.12.As expected,the Reynolds stress levels of the ribbon canopy were much lower than those of the other canopies and the maximum absolute Reynolds stress value was about 0.015.Even though the transverse profiles of Reynolds stress of the 8-branches canopy was similar to those of the cross canopy at position A,the Reynolds stress values were relatively smaller.As for the cross canopy,the absolute Reynolds stress values at position A were relatively higher than those at position B where−1.0R ＜y＜−0.6R.Moreover,for all these cases,at the region wherey≈−1.4R,the Reynolds stress values reduced to be approximately 0.

Figure 13 shows the normalized turbulent kinetic energy results at a Reynolds number of 33,314.As can be seen,the turbulent kinetic energy levels of the ribbon canopy were much lower than those of the other canopies.In addition,since the flow through gap formed a larger turbulent wake than the flow over arm(Figs.5 and 7),such a phenomenon was also reflected in TKE distributions.The influence region of TKE at position B(Fig.13d)was found to be larger than that at position A(Fig.13c).Moreover,as for the 8-branches canopy,TKE concentrated in the region where−1.1R＜y＜−0.5R.In our results,dark regions could also be found near thex-axis,which were caused by the retention line and should be neglected.

The transverse profiles of normalized turbulent kinetic energy are shown in Fig.14.The results also demonstrated that the TKE values of the ribbon canopy were smaller than those of the other canopies.The maximum TKE value for the ribbon canopy was found to be about 0.04,while for other two canopies,the maximum TKE value was about 0.09.As for the 8-branches canopy,the dependence of TKE on Reynolds number was minor,and the largest discrepancies between the case whenRe=74,362 and the other three cases appeared in the region where−1.0R＜y＜−0.6R.As for the cross canopy,the TKE values at position B were relatively higher than those at position A where−1.2R＜y＜−0.9R.Moreover,for all these cases,at the region wherey≈ −1.4R,the TKE values decreased to be less than 0.015.

Fig.12 The transverse profiles of normalized Reynolds stress where x=1.5 R.a Ribbon.b 8-branches.c Cross(position A).d Cross(position B)

These results clearly show that the geometry of the parachute canopies has apparent effects on the wake flow structures.Regarding this,when designing a parachute canopy,it is recommended to perform a comprehensive investigation on the flow structures in the wake of the canopy.This helps to obtain a better understanding of the relationship between the change of the canopy shape and the final aerodynamic performance of the parachute.In addition,data obtained in this paper can be used for validations of theoretical models and simulations in computational fluid dynamics.

Fig.13 Normalized turbulent kinetic energy distributions when Re=33,314.a Ribbon.b 8-branches.c Cross(position A).d Cross(position B)

4 Conclusions

Flow structures in the wakes of three types of parachute canopies were investigated using stereo-PIV.These parachute canopies were fabricated with the same surface area,and their geometries included ribbon canopy, 8-branches canopy,and cross canopy.We measured and analyzed both flow through the gap and over the arm of the cross parachute.The obtained results showed that the variation of the geometry of the parachute canopies had significant influences on the flow structures in the turbulent wakes of these canopies.The increase of Reynolds number does not lead to a dramatic variation in the distributions of thexcomponent of the velocity,vorticity,Reynolds stress,and turbulent kinetic energy in the wakes of these parachute canopies.The recirculation zone in the wake of the ribbon canopy formed at a further downstream region than that of the others.In addition,the normalized Reynolds stress and normalized turbulent kinetic energy of the ribbon canopy were found to be less than those of the others.

Fig.14 The transverse profiles of normalized TKE where x=1.5.a Ribbon.b 8-branches.c Cross(position A).d Cross(position B)

AcknowledgementsThis work was supported by the Science and Technology Commission of Shanghai Municipality (Grant 15ZR1442700)and the Fundamental Research Funds for the Central Universities.

1.Johari,H.,Desabrais,K.J.:Vortex shedding in the near wake of a parachute canopy.J.Fluid Mech.536,185–207(2005)

2.Cockrell,D.J.:The aerodynamics of parachutes,AGARD-AG-295(1987)

3.Maydew,R.C.,Peterson,C.W.:Design and testing of high performance parachutes,AGARDograph 319(1991)

4.Jorgensen,D.S.:Cruciform parachute aerodynamics.[Ph.D.thesis],University of Leicester,UK(1982)

5.Shen,C.Q.,Cockrell,D.J.:Aerodynamic characteristics and flow around cross parachutes in steady motion.J.Aircr.25,317–323(1988)

6.Shen,C.Q.,Cockrell,D.J.:Flow Field Characteristics Around Cuplike Bluff Bodies,Parachute Canopies,AIAA-91-0855-CP.AIAA,San Diego,CA(1991)

7.Peterson,C.W.,Strickland,J.H.,Higuchi,H.:The fluid dynamics of parachute inflation.Annu.Rev.Fluid Mech.28,361–387(1996)

8.Levin,D.,Shpund,Z.:Canopy geometry effect on the aerodynamic behavior of cross-type parachutes.J.Aircr.34,648–652(1997)

9.Stein,K.,Tezduyar,T.,Kumar,V.,etal.:Aerodynamic interactions between parachute canopies.J.Appl.Mech.70,50–57(2003)

10.Yagiz,O.E.,Albayrak,K.,Yildirim,R.O.:Experimental investigation of three rotating parachutes.J.Aircr.43,1574–1577(2006)

11.Johari,H.,Levshin,A.:Interaction of a line vortex with a round parachute canopy.J.Fluid.Struct.25,1258–1271(2009)

12.Han,Y.H.,Wang,Y.W.,Yang,C.X.,et al.:Numerical methods for analyzing the aerodynamic characteristics of cross parachute with permeability.In:AIAA Aerodynamic Decelerator Systems(ADS)Conference,Florida,AIAA 2013-1283,Mar 25–28(2013)

13.Xue,X.,Koyama,H.,Nakamura,Y.,et al.:Effects of suspension line on flow field around a supersonic parachute.Aerosp.Sci.Technol.43,63–70(2015)

14.Xue,X.,Nishiyama,Y.,Nakamura,Y.,et al.:Parametric study on aerodynamic interaction of supersonic parachute system.AIAA J.53,2796–2801(2015)

15.Gao,X.,Zhang,Q.,Tang,Q.:Fluid-structure interaction analysis of parachute finite mass inflation.Int.J.Aerosp.Eng.28,1438727(2016)

16.Gao,X.,Zhang,Q.,Tang,Q.:Numerical modelling of Mars supersonic disk-gap-band parachute inflation.Adv.Space Res.57,2259–2272(2016)

17.Desabrais,K.J.:Velocity field measurements in the near wake of a parachute canopy.[Ph.D.thesis],Mechanical Engineering Department,Worcester Polytechnic Institute,Worcester,MA,USA(2002)

18.Wernet,M.P.,Locke,R.J.,Wroblewski,A.:Application of stereo PIV on a supersonic parachute model.In:47th AIAA Aerospace Sciences Meeting,AIAA 2007-0070,Jan 5–8(2007)

19.Schairer,E.T.,Heineck,J.T.,Walker,L.A.,et al.:Simultaneous,unsteady PIV and photogrammetry measurements of a tensioncone decelerator in subsonic flow.In:15th International Sympo-sium on Applications of Laser Techniques to Fluid Mechanics,Lisbon,Portugal,July 5–8(2010)

20.Sengupta,A.,Longmire,E.,Ryan,M.,et al.:Performance of a conical ribbon drogue parachute in the wake of a subscale Orion command module.In:Aerospace Conference,2012 IEEE,Big Sky,MT,Mar 3–10(2012)

21.Jin,Z.,Pasqualini,S.,Qin,B.:Experimental investigation of the effect of Reynolds number on the flow structures in the wake of a circular parachute canopy.Acta Mech.Sin.30,361–369(2014)

22.Jin,Z.,Pasqualini,S.,Yang,Z.:Experimental investigation of the flow structures in the wake of a cross parachute canopy.Euro.J.Mech.B Fluids 60,70–81(2016)