基于自适应Voronoi检测器的故障检测算法

尹中川　徐遵义　韩绍超　王俊雪

(山东建筑大学计算机科学与技术学院　山东 济南 250101)

0　引　言

现代工业随着技术水平的不断推进，工业生产现场人员不断减少，生产规模不断扩大，工业生产设备也随之大型化、复杂化，在石化、冶金、电力等过程工业尤为显著，设备故障停机会造成巨额损失。而在积累的历史数据中又很难获取足够的故障样本来训练诊断模型。如何在没有或少量的故障样本下，利用设备正常工作时的数据样本来判别设备运行的情况，准确预测故障，对保障设备安全运行，提高工业生产效益具有十分重要的意义。

生物免疫系统能够在不需要先验知识的条件下，通过自我学习，逐渐提高自身的免疫能力，达到有效防御外来物质，保护本体的机制。根据生物免疫系统的这种机制，Forrest等[1]提出了用于异常检测的二进制反面选择算法。之后，Dasgupta[2]教授领导的课题组，又提出了等径实值检测器。文献[3]在此基础之上，提出了可变半径实值检测器。此后又有学者相继提出了超球体检测器、超矩形检测器和超多类型检测器等[2,8,10]。上述检测器都在一定程度上减少了检测器的数量，提高了对正常样本的覆盖率[3-5]。但并没有完全覆盖自体空间并消除检测器之间的孔洞。

如何设计一种检测器既能保证检测器数量上的简约，又能消除检测器之间的孔洞并完全覆盖正常样本，对提高检测精度和效率，具有重要意义。

1　传统实值否定选择算法

否定选择算法借鉴生物免疫系统中胸腺T细胞生成时的否定选择过程，模拟了免疫细胞的成熟过程，删除通过系统对异常变化的成功检测而使免疫系统发挥作用[3]。成功检测异常的关键是系统能够准确区分自己和非己信号。算法通过随机产生检测器，并上出那些检测到自体的检测器。算法包括耐受和检测两个重要阶段[5]，具体步骤见算法1。

算法1否定选择算法

1) 随机产生半径相同的候选检测器。

2) 对每一个候选检测器计算与每一个自体元素间的亲和度，如果检测器识别出了任何一个自体元素，那么删除该检测器，否则认为该检测器已经成熟，将其加入检测器集合中；步骤1)和步骤2)如图1所示。

图1　检测器的成熟过程

3) 将待测数据与成熟检测器集合中元素逐个对比，如果出现匹配，则证明待检测数据为非自体数据，即异常数据。步骤3)如图2所示。

图2　数据检测识别过程

传统实值检测器的每个检测器的半径都是相同的，这导致了较高的重复覆盖率，增加了检测器的数量，以及不能很好地匹配一些形状复杂的非自体空间。可变半径的实值否定选择算法是在实值否定选择算法的基础上，产生半径可变的检测器，且当两个检测器的重复覆盖率超过临界值时，会将较小的检测器删除。这样既提高了检测器的覆盖率，也减少了检测器的数量空洞，但增加了检测器训练过程的时间。

2　自体空间确定

否定选择算法的首要工作是确定自体空间，之后用来筛选成熟的检测器。因此自体范围的精确度直接影响到了检测精度[8-9]。本文基于密度的聚类获取位于自体空间边界的低密度样本，通过这些边界样本确定自体空间的边界。下面介绍使用OPTICS聚类方式获取自体空间的边界样本的过程。

OPTICS聚类是基于密度的聚类方式，其思想和DBSCAN非常类似，但是和DBSCAN不同的是，OPTICS算法可以获得不同密度的聚类[7]。具体流程见算法2。

算法2OPTICS聚类算法

输入：数据样本D，初始化所有点的可达距离和核心距离为MAX，半径ε，和最少点数MinPts。

1) 建立两个队列：有序队列(核心点及该核心点的直接密度可达点)，结果队列(存储样本输出及处理次序)。

2) 如果D中数据全部处理完，则算法结束，否则从D中选择一个未处理且未核心对象的点，将该核心点放入结果队列，该核心点的直接密度可达点放入有序队列，直接密度可达点并按可达距离升序排列。

3) 如果有序序列为空，则回到步骤2)，否则从有序队列中取出第一个点。

(1) 如果该点不在结果队列判断该点是否为核心点，不是则回到步骤3)，是的话则将该点存入结果队列。

(2) 该点是核心点的话，找到其所有直接密度可达点，并将这些点放入有序队列，且将有序队列中的点按照可达距离重新排序，如果该点已经在有序队列中且新的可达距离较小，则更新该点的可达距离。

4) 重复步骤3)，直至有序队列空。

5) 算法结束。

3　冯洛诺伊检测器

冯洛诺伊图又叫泰森多边形，是由一组连接两相邻点直线的垂直平分线组成的连续多边形组成[6]。冯洛诺伊图是对空间的一种剖分，其特点是多变形内的任何位置离该多边形的样点的距离最近，离相邻多边形内样点的距离远，且每个多边形内含且仅包含一个样点。

3.1　自适应冯洛诺伊检测器

本文针对实值否定选择算法无法消除孔洞的缺陷，依据OPTICS[7]聚类，根据数据的密度来区分自体空间的边界数据，依靠冯洛诺伊图来划分问题空间的区域。并借助冯洛诺伊图只依靠周围点来建立的原理，针对实时的检测效果，对检测器进行实时更新。

3.2　存储结构定义

数据节点定义

typedef struct DataNode{

//位置信息

}

冯洛诺伊网格节点定义

typedef struct VorinoiPoint{

int position[MaxDimension];

//位置信息

struct VorinoiPoint * nextPoint[Max];

//邻边节点

}

检测器结构定义

《花间集》皆唐末五代时人作，方斯时天下岌岌，生民救死不暇，士大夫乃流宕如此，可叹也哉！或者亦出于无聊故耶？笠泽翁书。

typedef struct Detector{

struct DataNode * core;

//检测器核心点

struct VorinoiPoint * points[Max];

//检测器边缘端点

}

3.3　自适应冯洛诺伊检测器生成算法

自适应冯洛诺伊检测器生成算法的基本步骤如下：

(1) 通过Optics聚类生成对应的核心距离矩阵。

(2) 根据3σ准则筛选出内外边界数据。

(3) 根据筛选出的数据生成冯洛诺伊网格图。

(4) 外边界数据所在网格即为冯洛诺伊检测器。自适应冯洛诺伊检测器生成算法如图3所示。

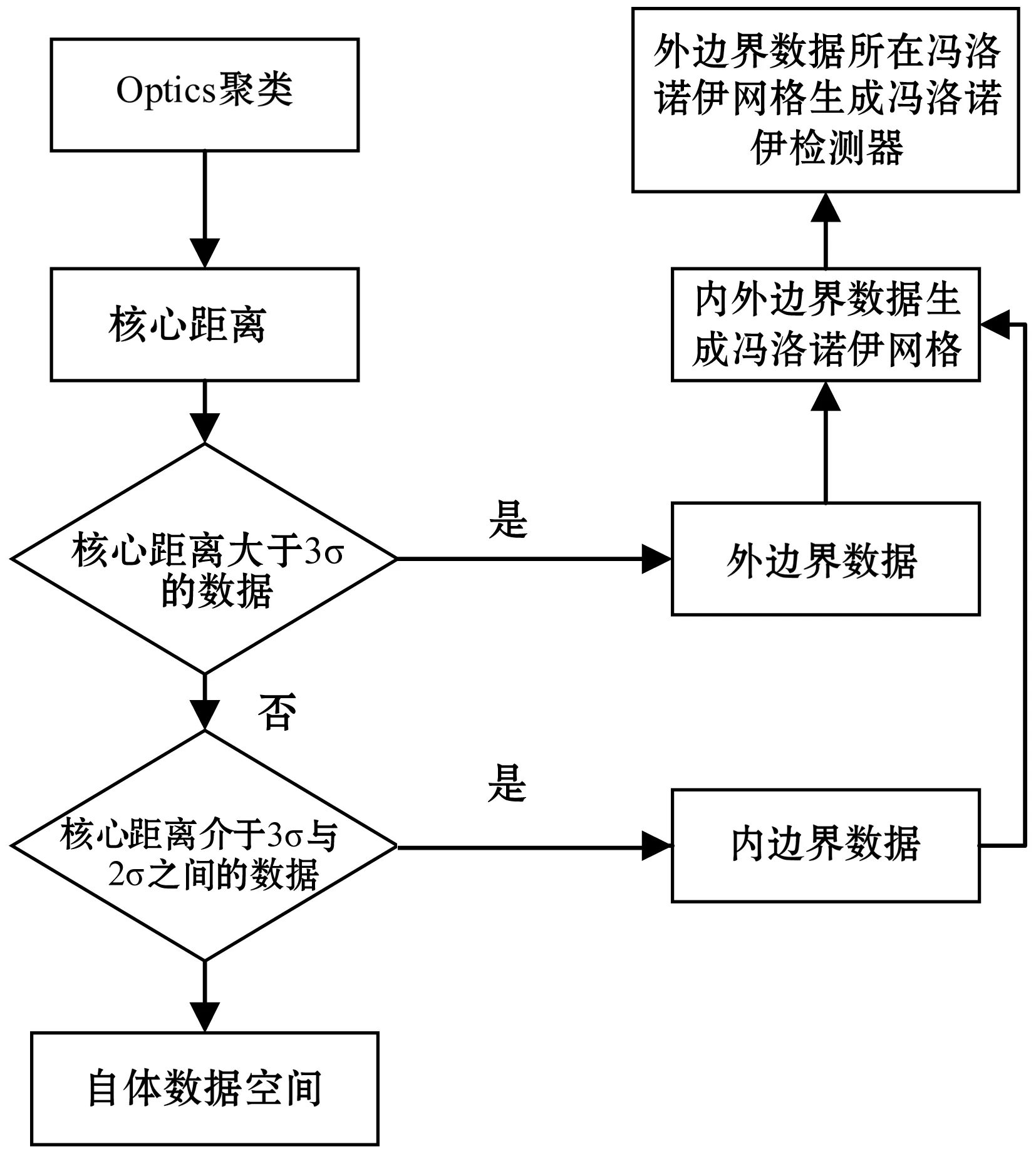
图3　自适应冯洛诺伊检测器生成算法

3.4　自适应冯洛诺伊检测器在线更新算法

自适应冯洛诺伊检测器在线更新算法的基本思想:新的冯洛诺伊网格的生成只依赖对应网格的相邻网格，当出现错误检测时，将误判点插入检测器内，与周围最近的几个检测器一起重新生成一个新的检测器，并更新周围的检测器。步骤见算法3。

算法3自适应冯洛诺伊检测器在线更新算法

1) 对所有检测器到错误检测数据按照距离进行排序，并生成队列。

2) 访问队首检测器，并出队，以错误点到检测器核心点的中位线生成冯洛诺伊边界直线y=f(x)，且设置边界的两端点为空，添加到新的检测器边界中。

3) 访问队首并出队，以错误点到该检测器的核心点的中位线生成新的冯洛诺伊边界直线，若新的冯洛诺伊边界直线与存在的新检测器边界平行，且位于错误点的一侧，则进行下一步；否则，将直线加入到新的检测器边界中，并更新边界端点。

4) 若新的检测器的边界断电是否所有都非空，则输出新的检测器，并根据周围检测器对应的新检测其边界，更新生边界；否则返回3)。

4　实验分析

4.1　Iris数据仿真实验

由于工业生产中的数据具有连续性，而正常数据与异常数据也具有线性可分的特性，考虑到Iris数据非线性可分样本存在，在对Iris数据进行实验之前需要使用多项式核函数对Iris数据进行空间变换[11]。

核函数公式：

K(Xi,Xj)=(Xi·Xj+1)2

为了方便实验结果的观察，Iris数据进行核函数变换后，再利用主元分析法(PCA)进行降维，将数据压缩到二维，最后设定virginica数据中的30个为空间中的自体样本。分别使用RNSA算法和V-detector算法与Voronoi-RNSA算法生成检测器，比较它们在95%期望覆盖率下的检测器的生成时间和数量以及对非virginica数据的识别率。

RNSA算法、V-detector算法和Voronoi-RNSA算法生成的检测器数量分别为67 718和15，检测器生成时间分别为33.06、4.05和5.28 s，对非virginica数据的识别率分别为90%、91%和98%。可以看出Voronoi-RNSA算法相对于传统否定选择算法训练时间较短，识别率较高。三种算法生成图像如图4-图6所示。

图4　RNSA算法检测器生成图

图5　V-detector算法检测器生成图

图6　Voronoi-RNSA算法检测器生成图

从图4中可知由于RNSA算法检测器存在大量冗余，且由于半径固定，自体空间的边界匹配并不理想。

从图5中可知V-detector算法相对RNSA算法，精简了检测器的数量，且在自体边界附近可生成半径较小的检测器，边界匹配度有一定程度提高。但由于检测器是随机生成的，需要大量的迭代计算才能对边界的匹配度进一步提高。

从图6中发现，Voronoi-RNSA算法边界由自体空间的外边界数据点确定不需要迭代计算且检测器的数量依赖于边界的复杂程度，且不存在孔洞。自体空间由外边界和内边界数据确定，在自体样本充足的情况下，可以精确描述自体边界。

4.2　中国华北某电厂振动类型数据实验分析

华北某电厂轴承振动历史数据共29个测点，数据具有海量、无标签的特点，且故障样本极少，无法人为指定自体样本空间。

首先对数据进行主元分析，得到两个主成分，其贡献度超过98%。能够表征绝大部分数据信息。之后，分别使用RNSA算法和V-detector算法与Voronoi-RNSA算法生成检测器，比较它们在90%期望覆盖率下生成的检测器对自体空间边界的匹配情况。三种算法生成图像如图7-图9所示。

图7　RNSA算法检测器生成图

图8　V-detector算法检测器生成图

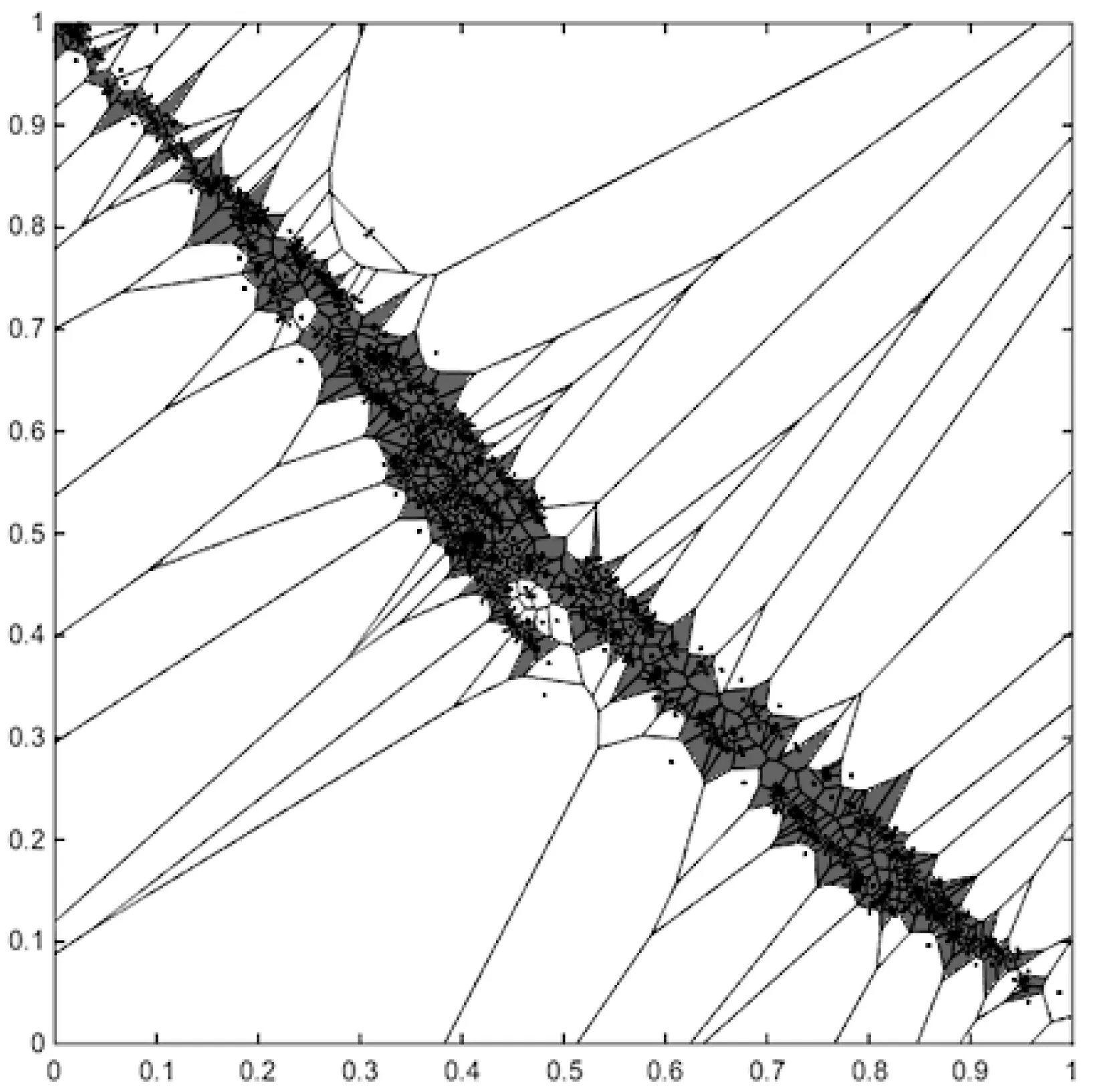
图9　Voronoi-RNSA算法检测器生成图

如图7所示，RNSA算法在生成大量检测器后，自体空间边界附近仍然具有大量孔洞存在，真实的检测精度难以保证。

如图8所示，V-detector算法对自体空间边界的匹配度有所提高，但仍然存在孔洞。算法收敛后，检测器的随机生成机制很难在孔洞处生成新的检测器。

如图9所示，Voronoi-RNSA算法使用内外边界数据生成自体空间与检测器，检测器可以很好地匹配自体空间边界。此外，还可以添加有限的异常数据，对边界检测器进一步优化。

以上实验表明，传统的否定选择算法不可避免存在着孔洞，而这些孔洞更多存在于自体数据的边界，然而真实数据往往具有连续性，故障数据很可能会存在于自体数据的边界附近。因此真实的检测精度要比检测器的覆盖率低很多。Voronoi-RNSA算法基于内外边界数据生成检测器，能够避免孔洞的产生，提高了检测精度，极大地提高了否定选择算法在实际故障检测中的精度。此外，Voronoi检测器能够根据实际的误判来实时修改自体边界，从而检测系统在一个较长时间运行训练后，能够得到更高的检测精度。

5　结　语

否定选择算法是人工免疫系统中的重要环节，RNSA算法采用实值空间编码抗原和抗体生成检测器，V-detector算法采用了可变半径的检测器，也已经取得了较好检测效果。然而，使用传统的检测器定义方式会导致三个缺陷：(1) 无法避免非自体空间中孔洞的产生，从而在达到一定的覆盖率后很难再提升，会有一定的误报率；(2) 无法避免检测器的重复覆盖，检测器的实际覆盖效率并不高，导致检测器的数量过多；(3) 检测器的耐受训练过程占用大量时间，检测器生成效率过低。

针对上述问题，针对机械设备的数据特点提出了一种基于自适应冯洛诺伊检测器的否定选择算法(Voronoi-RNSA)。首先通过OPTICS聚类找到自体空间的外边界和内边界数据，之后根据内外边界数据生成冯洛诺伊网格，外边界所在的冯洛诺伊网格即是生成的检测器。该检测器生成方式极大地减少了检测器耐受训练时间，并避免了重复覆盖的问题，大大提高了检测器实际覆盖效率，减少了检测器的数量，从理论上排除了孔洞的产生。实验证明，Voronoi-RNSA算法比经典的RNSA算法和V-Detector算法具有更高的检测精度和更好的检测器生成质量。

由于冯洛诺伊网格图在高维空间中生成过慢，使用Voronoi-RNSA算法对高维数据进行故障检测，需要将高维数据压缩到低维空间后在进行，从而影响了其在高维数据中的应用推广。而自体空间的描述精度直接影响到检测器耐受过程，是影响检测精度的重要因素。因此，可针对高维数据和自体空间的界定进行进一步的研究。

[1] Forrest S, Perelson A S, Allen L, et al. Self-Nonself Discrimination in a Computer[C]// Research in Security and Privacy, 1994. Proceedings. 1994 IEEE Computer Society Symposium on. IEEE, 1994:202-212.

[2] Dasgupta, Dipankar, Yu, Senhua, Nino, Fernando. Recent Advances in Artificial Immune Systems: Models and Applications[J]. Applied Soft Computing, 2011, 11(2):1574-1587.

[3] Chen L F. An improved negative selection approach for anomaly detection: with applications in medical diagnosis and quality inspection[J]. Neural Computing & Applications, 2013, 22(5):901-910.

[4] 徐学邈, 王如根, 侯胜利. 基于反面选择原理的智能融合故障检测模型及其应用[J]. 系统工程与电子技术,2009,31(8): 2030-2032.

[5] Tao Yuan, Hu Min, Yu Yanlin. A Novel Negative Selection Algorithm for Recognition Problems[J]. International Journal of Hybrid Information Technology,2015,8(11):101-112.

[6] 陈文, 李涛, 刘晓洁,等. 一种基于自体集层次聚类的否定选择算法[J]. 中国科学:信息科学, 2013, 43(5):611-625.

[7] 张凤斌, 王天博. 实值n维混沌映射否定选择算法[J]. 计算机研究与发展, 2013, 50(7):1387-1398.

[8] 孙添, 何国良. 基于K-均值聚类和泰森多边形的异常值检测方法[J]. 重庆文理学院学报, 2016, 35(2):10-13.

[9] 党秋月, 陆月明. 基于OPTICS可达图的自动识别簇方法[J]. 计算机应用, 2012, 32(A02):19-21.

[10] Aydin I, Karakose M, Akin E. Chaotic-based hybrid negative selection algorithm and its applications in fault and anomaly detection[J]. Expert Systems with Applications, 2010, 37(7):5285-5294.

[11] 芦天亮,郑康锋,傅蓉蓉,等.基于阴性选择算法的异常检测系统黑洞覆盖优化[J].通信学报,2013(1):128-135.

[12] Li Dong, Liu Shulin, Zhang Hongli. A negative selection algorithm with online adaptive learning under small samples for anomaly detection[J]. Neurocomputing, 2015, 149(C):515-525.

[13] 刘颖慧.基于人工免疫系统的异常状态检测及故障诊断研究[D].上海：上海交通大学，2013.