基于收缩应变法的地铁铝合金地板FSW数值模拟
2018-04-17魏诗萌闫占奇杨鑫华
魏诗萌 ,闫占奇 ,迟 哲 ,杨鑫华
(1.大连交通大学材料科学与工程学院,辽宁大连116028;2.中车长春轨道客车股份有限公司,吉林长春130062;3.辽宁省轨道交通装备焊接与可靠性重点实验室,辽宁大连116028)
0 前言
铝合金因其较高的比强度、良好的工艺性等特点被逐渐广泛应用于轨道车辆车体结构中[1]。传统的MIG焊在焊接铝合金时常出现裂纹、气孔、未熔合、未焊透等焊接缺陷[2]。搅拌摩擦焊作为一种新兴的焊接工艺具有不易产生气孔和裂纹等缺陷[3],不产生烟尘、飞溅和辐射,避免危害焊工人身健康,生产效率高[4]。但搅拌摩擦焊与传统的熔化焊均存在焊接过程中加热与冷却不均匀,因此搅拌摩擦焊的焊后变形与残余应力的精确预测与控制成为实际生产需要考虑的一个重要问题。
有限元分析方法是预测焊后残余应力和焊接变形的方法之一,但仍存在诸多问题。传统的热弹塑性法计算结果精确,但计算时间长,收敛困难,不适用于大型构件有限元分析[5-6]。上田幸雄等人提出的固有应变法较好地提高了焊接有限元分析模拟计算效率[7-9]。大连交通大学杨鑫华等人在分析焊后变形与残余应力产生的机理后结合固有应变理论,实现了基于收缩应变方法来解决大型构件焊接变形仿真计算[10]。收缩应变是指构件在经过热循环后残留在构件中并引起残余应力和变形产生的应变(也有学者称其为残余应变),是焊接残余应力与变形的根源,其大小和分布规律是影响变形仿真计算的关键。收缩应变可通过实验数据和经验数据分析或热弹塑性计算结果获得。
本研究围绕某型号地铁铝合金地板搅拌摩擦焊接变形控制问题,在分析地板结构与工艺的基础上,截取地板局部型材结构,建立合适的热源模型,同时考虑局部模型在整体结构的连接状态与约束位置,建立边界条件,进行有限元分析。在获得焊核及热影响区收缩应变分布基础上,实现了地板整体结构FSW仿真计算。通过与实测结果对比,验证了该方法的可行性与合理性,为实际生产中实现面向变形控制的焊接工艺优化提供了方法参考。
1 地板局部结构模型建立与收缩应变提取
1.1 地板局部结构模型建立
截取全尺寸地板模型中尺寸300 mm×700 mm的焊缝结构作为局部模型,划分网格如图1所示。焊缝区最小单元尺寸1 mm×1 mm×1 mm,为节省计算时间,提高计算效率,远离焊缝处采用较大的网格进行划分。局部结构整体单元数为97 650个。对局部结构进行顺序热力耦合计算过程中,材料各项性能随着温度变化而改变,6005A-T6的材料属性如图2所示。
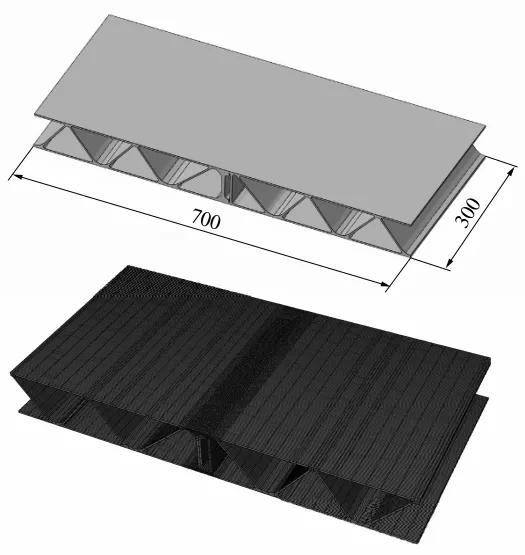
图1 地板局部几何与网格模型
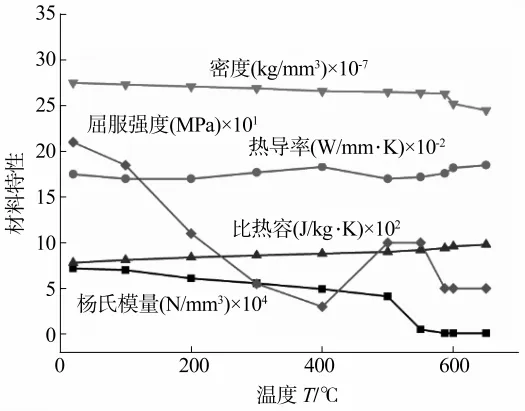
图2 6005A-T6的材料属性
边界条件设置对仿真计算结果影响很大。在局部模型边界条件设置过程中,既要考虑局部结构与型材整体连接关系,又要尽可能体现实际生产过程中地板两端有挡块、两侧有压爪等机构保证焊接过程的刚性约束(见图3)。因此,在局部结构焊缝下与焊缝两侧施加Z向约束,两端施加X向约束,两侧施加YZ约束来保证精度。
1.2 热源模型与搅拌头的力作用模型
搅拌摩擦焊的总热量来源于两部分:一是搅拌头和工件之间摩擦产生,二是焊接区域材料的塑性变形。在模拟中假设这些热量分布在3个区域:一是轴肩和工件之间的接触面,二是圆锥形搅拌针侧面作用的区域,三是搅拌针底面作用的区域。根据文献[11]中关于地板搅拌摩擦焊的建模与分析内容,建立搅拌摩擦焊热源模型。

图3 实际焊接过程中的工装应用
1.2.1 轴肩产热模型
轴肩表面示意如图4所示。R1为搅拌头轴肩半径,R2为搅拌针根部半径,轴肩产热的有效区域为R1与R2之间的圆环面积。假设搅拌头顶锻压力均匀作用在轴肩上,则半径r、宽度为dr的微圆环上的摩擦力为
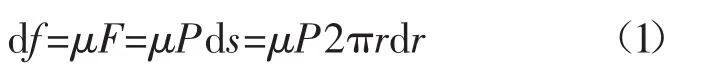
式中 μ为摩擦系数;P为轴肩压力。
微圆环上的力矩为

对其积分得到扭矩为
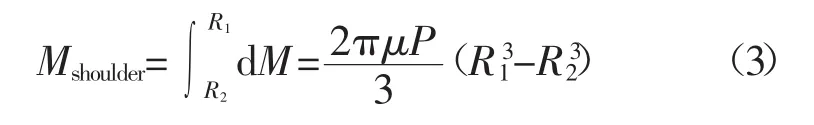
从而轴肩产热功率为
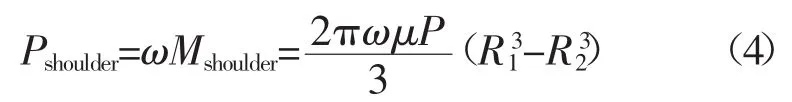
轴肩产热热流密度为
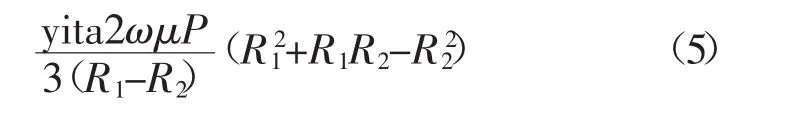
式中 yita为产热总效率。

图4 轴肩表面示意
1.2.2 搅拌针产热模型
(1)搅拌针侧面产热模型。
搅拌针示意如图5所示,圆锥角为2α,搅拌针根部和端部半径分别为R2和R3,取微圆台半径为r,厚度为 ds,则侧面积为

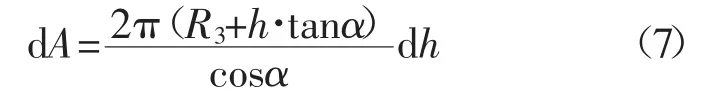
则圆锥台搅拌针的侧面积为

微圆环产生的力矩为
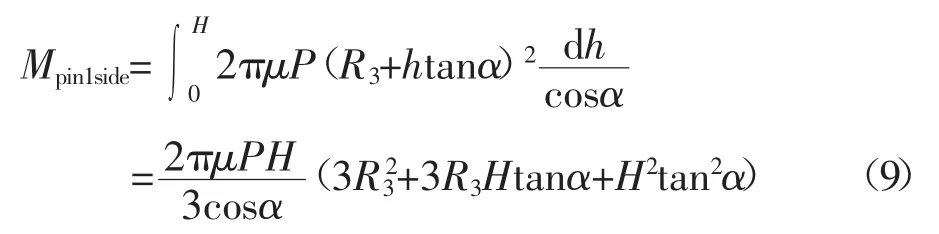
搅拌针侧面产热功率为
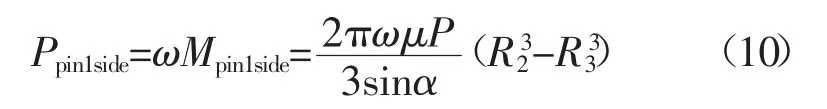
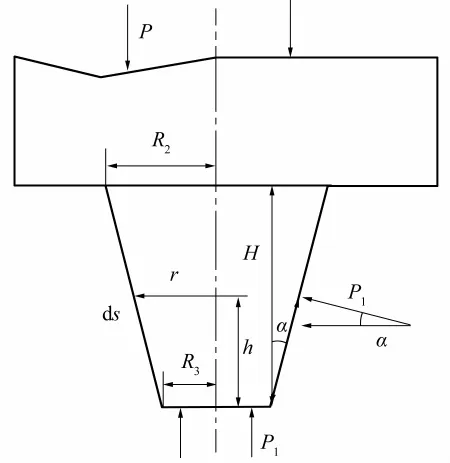
图5 搅拌针示意
(2)搅拌针底面产热模型。
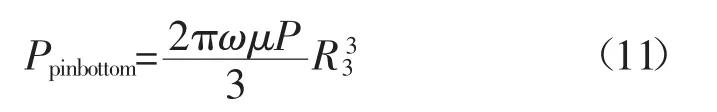
搅拌针产热热流密度为
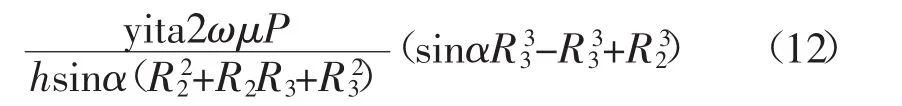
1.2.3 搅拌头力学模型
文献[12]表明[12],搅拌头的机械作用会对搅拌摩擦焊接残余应力的分布产生显著影响,也会影响焊接残余变形,力学模型同样引入了搅拌头的力学作用,将搅拌头的下压力考虑为均匀分布的面力,添加在模型上表面搅拌头作用区域内。搅拌头的工作扭矩考虑为搅拌头范围内分布的圆周切向力,切向力以体力的方式添加到搅拌头作用区域内靠近上表面的一层积分点上[13]。
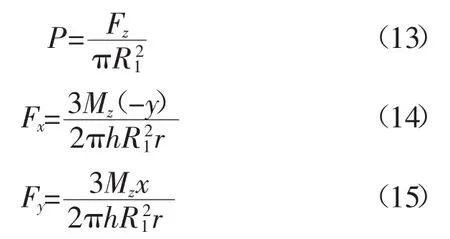
式中 Fz为搅拌头的下压力;Mz为转矩;P为添加到模型上的压力;Fx,Fy为添加到模型上的切向力;x,y为积分点的坐标值。
1.3 局部模型收缩应变计算
根据生产过程中实际采用的搅拌针形状、尺寸和相应工艺参数,包括搅拌头倾角、主轴转速、焊接速度、顶锻力等,在有限元分析中采用相同参数对搅拌头轴肩尺寸、顶锻压力等进行赋值,基于Abaqus有限元仿真平台,实现局部模型FSW焊接过程的仿真计算。
1.3.1 焊接仿真模拟结果与分析
通过顺序热力耦合计算得到的焊接温度场如图6所示,模拟得到的温度场与实际测量结果在分布趋势上完全一致,但温度数值上略有误差,焊缝最高温度约为520℃。利用该温度场进行力学分析计算,从热载荷的角度来看是可接受的。值得注意的是,温度场模拟中使用的热源模型是对称模型,所以得到的温度场分布关于焊缝中心线对称,这与一些实验结果稍有区别。实际搅拌摩擦焊接中,因为前进侧和返回侧受到的搅拌摩擦作用不同,所以温度分布不对称,前进侧略高于返回侧。Buffa等人[14]研究温度场分布,发现将温度场近似处理为对称分布虽然会对接头残余应力分布造成一定的影响,但这种影响并不显著。

图6 局部结构温度场
通过顺序热力耦合计算得到的局部模型的Mises应力场如图7所示,在稳定焊接阶段的Mises应力最大值为225 MPa,其最大区域主要集中在焊缝处,低于6005A-T6的屈服极限241 MPa,考虑到加工硬化等因素的影响,Mises应力值在理想范围内。
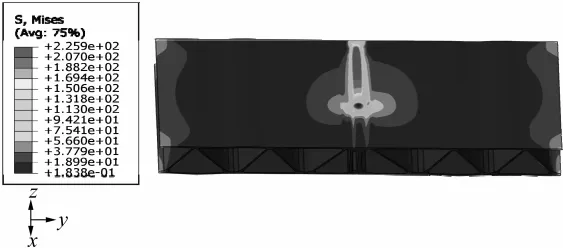
图7 局部结构应力场
1.3.2 收缩应变的提取
收缩应变法预测焊接变形是利用焊缝及其附近的收缩应变作为初始应变,只进行一次弹塑性有限元计算获得整个结构的焊接变形。需提取局部模型稳定焊接时焊缝和热影响区附近的塑性应变作为整体模型计算时的初始应变。
稳定焊接阶段整体收缩应变、横向收缩应变、纵向塑性应变如图8所示。塑性应变区域均集中在焊缝处,数值上由焊缝表面为负到焊缝内为正变化,在型材其他结构应变值几乎为0,因此仅提取焊缝附近的应变值,即可针对整体地板模型进行计算。由于在焊缝范围内应变值变化较为稳定,且垂向应变值与横向、纵向应变值相差悬殊,在确保计算精度的前提下提高计算效率,将纵向、横向应变以平均值的形式求出,垂向应变值为0施加在整体地板模型上。
2 地铁地板仿真模拟与实际结果对比
构件在实际焊接过程中受到局部不均匀加热与冷却的影响,在冷却后残余的应变是导致构件产生焊接变形与残余应力的源头,其大小与分布状态最终决定焊后焊接变形趋势和残余应力分布状态。
焊接过程中高温和材料非线性发生在焊缝附近的很小区域内,该区域的塑性变形是导致整体结构变形的根本原因(见图9);远离焊缝区域是弹性变形区,当焊接过程结束,弹性变形会消失,对释放后的焊接变形没有太大影响。如果得到焊缝及其附近区域的收缩应变的大小和分布状态,将其作为初始应变赋予地板的焊缝及热影响区附近,就可通过一次线性计算快速获得地板的焊后变形与残余应力。
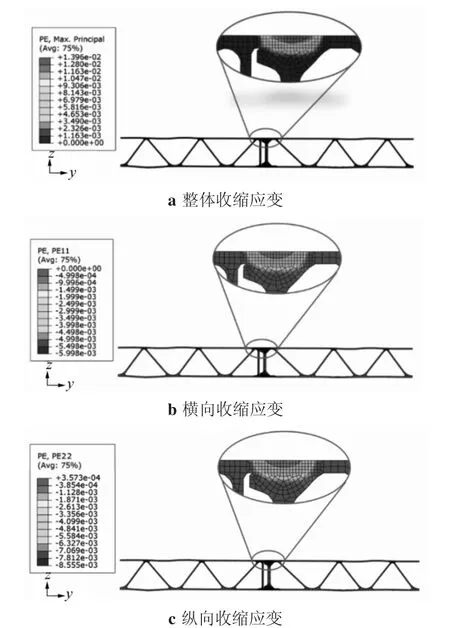
图8 收缩应变提取示意

图9 焊缝附近变形引起整体变形
2.1 地板整体有限元模型建立
地板模型由两块19 110 mm×497 mm×70 mm、一块19110mm×575mm×70mm和一块19 110 mm×452 mm×70 mm的地板型材依次对接而成,如图10所示。焊缝附近的结构与前文所提取的局部型材结构完全一致。采用8节点六面体单元划分几何体网格,模型单元总数351 972,为保证计算精度,细化焊缝及热影响区的单元,独立分组,结构与地板局部模型一致。为提高计算效率,采用缩减积分单元,单元类型为C3D8R。

图10 地板几何模型
在建立地板网格模型后,对其进行材料、几何约束以及输出的预定义场等相关设置。采用收缩应变法计算时,无需考虑温度对材料属性的影响,仅输入密度、塑性等机械物理性能。
约束条件与地板局部模型完全一致,如焊缝下的垫板,焊接时位于焊缝两侧的压铁、地板两端的挡块、地板两侧的压爪等。仿真中焊接顺序的制定严格按照实际的焊接顺序进行。
2.2 基于收缩应变的地铁地板有限元计算
通过收缩应变法计算得到的地板整体焊接变形云图如图11所示,地板整体变形趋势为整体上凸的翘曲变形。经分析,引起翘曲变形的原因为:①焊缝处产生的横向收缩所引起的翘曲变形,在现有工艺条件下,正面反面每条焊缝在垂向变形相互叠加下导致了地板整体为上凸的翘曲变形;②焊缝区域由于焊接过程中焊缝上下表面不均匀受热,引起局部塑性变形并产生了比容不同的组织,形成焊缝拉应力;③拉应力的作用点处在焊缝附近,产生横向弯曲所需的弯矩,使得结构产生横向的挠曲变形。从模拟数值上看,变形较大区域出现在地板中部,这可能是因为中部两条焊缝之间距离较近,产生翘曲变形在横向上相互叠加造成的。并且由于焊接起始端与结束端重叠,最大值也位于此处。
2.3 仿真与实测结果的对比分析
严格按照制定的焊接顺序、搅拌头转速等工艺进行焊接,焊接完成后,采用测量样板测量地板模型变形,为避免实际生产中可能导致的实验误差,进行多次实验,并对实验结果进行平均化处理,其挠度值由两侧向中间依次增大,最大挠度值约为3.8 mm。
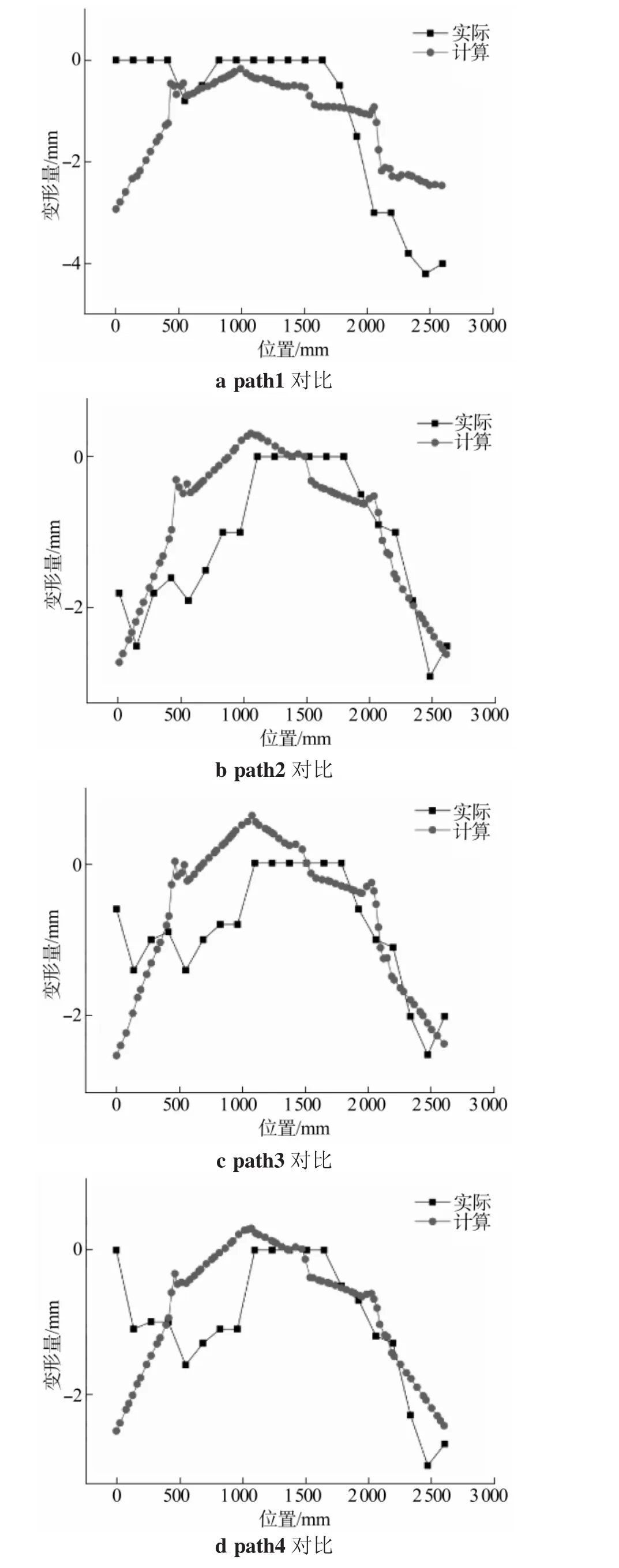
为便于比较实测与模拟结果,并考虑到地板长度因素,在地板正面选取将地板沿长度方向等分的7条参考线(见图12)作为基准,将模拟结果与实验数据进行对比来验证该方案的可行性。模拟结果与实验数据对比如图13所示。

图11 焊接变形云图

图12 参考线示意图
由图13可知,在整体变形趋势上,模拟结果与实际测量结果的契合度较高,除path5有一部分变形趋势与实际有出入外,其他部分变形趋势与实际测量结果几乎一致。整体变形趋势呈山峰状,峰值集中在约1 000 mm。在趋势相近部分,模拟结果与测量结果相差最大不超过0.5 mm。造成模拟与实际测量结果不同的原因可能为:①在实际焊接生产过程中,尤其是在焊接背面焊道与测量时,整体吊装地板的过程中容易对地板两侧产生垂向拉伸作用,导致模拟结果在起始和结束端与测量结果有一定误差;②在进行有限元分析建模与计算时,为提高建模和效率,收缩应变是经过平均简化的应变;③仿真的边界条件设置方法也会在计算过程中加大对地板的刚性影响,一定程度上影响计算结果,从而导致产生误差。
3 结论
(1)建立了地铁地板局部结构的几何与网格模型,运用顺序热力耦合方法对地板局部结构进行有限元分析计算。焊后残余应力最大值为230 MPa,小于6005A-T6铝合金的屈服极限241MPa;焊接过程中焊缝最高温度约为520℃,低于6005A-T6铝合金的熔点。
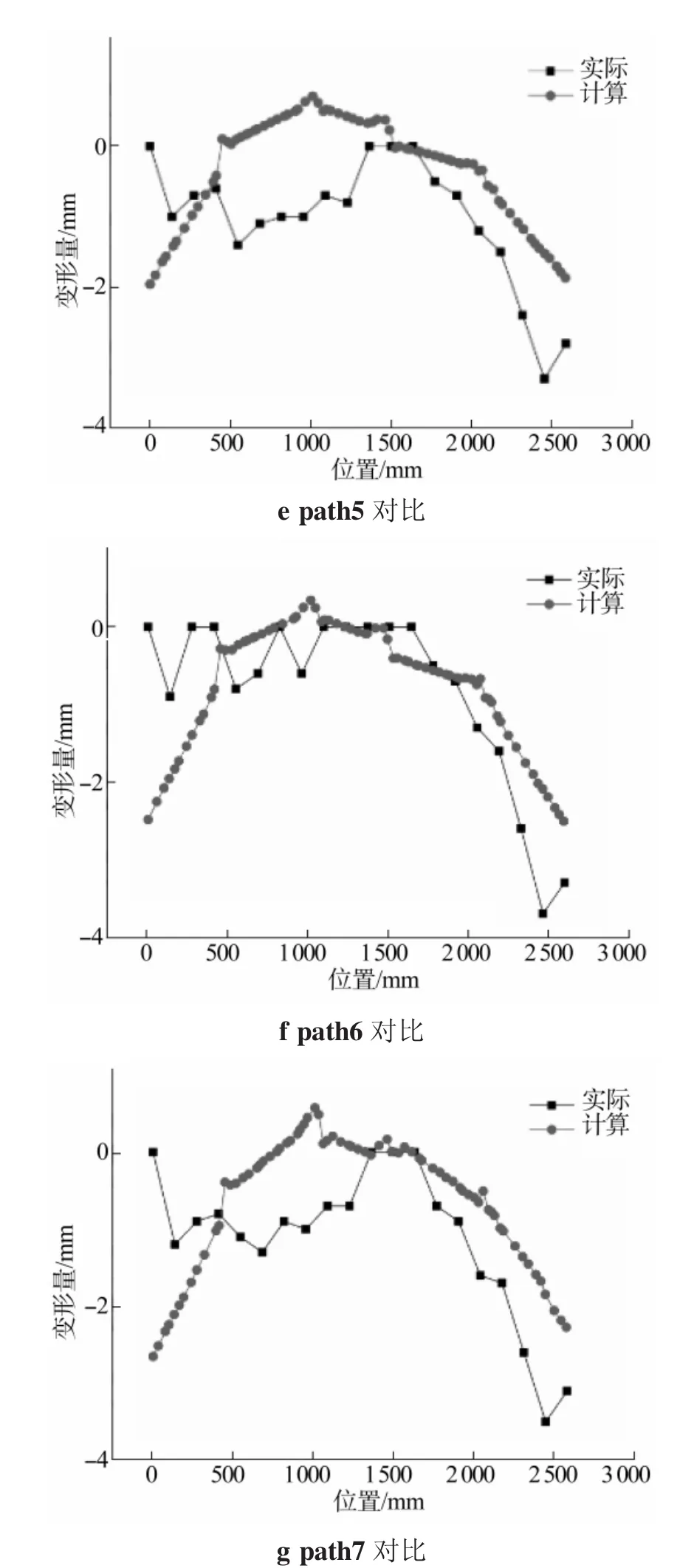
图13 模拟结果与实际测量结果对比
(2)从地板局部结构有限元分析结果中提取收缩应变,利用收缩应变法完成6005A-T6铝合金地板有限元模拟计算,经过有限元分析得到的地板焊接变形控制在理想范围,焊后变形最大值为3.5 mm。
(3)对比模拟结果与实验结果,变形趋势与实际测量情况一致,模拟结果与实际测量结果相差不超过0.5 mm。表明该方法对此类大型结构进行焊接变形仿真是可行的,为实现焊接顺序的优化设计等相关研究提供方法基础。
参考文献:
[1]杨巨平.铝合金材料在铁路货车上的应用研究[J].铁道车辆,2015,53(6):24-5.
[2]李会,郭继祥,何小勃,等.铝合金MIG焊常见焊接缺陷分析及预防措施[J].电焊机,2013,43(4):72-6.
[3]李程锦,王陆钊,刘其鹏,等.搅拌头几何参数及倾角对搅拌摩擦焊接质量影响的数值分析[J].大连交通大学学报,2017,38(5):70-74.
[4]朱卫,钟磊,岳译新.基于铝合金型材搅拌摩擦焊热力耦合有限元分析研究[J].电力机车与城轨车辆,2015(6):25-29,36.
[5]刘文龙.搅拌摩擦焊接全过程热力耦合有限元模拟研究[D].江西:南昌航空大学,2013.
[6]吴言高,李午申,邹宏军,等.焊接数值模拟技术发展现状[J].焊接学报,2002,23(3):89-92.
[7]Wang J,Ueda Y,Murakawa H,et al.Improvement in numerical accuracy and stability of 3-D FEM analysis in welding[J].Welding Journal,1996,75(4):129-134.
[8]汪建华.焊接变形和残余应力预测理论与计算——发展及应用前景[A].第十次全国焊接会议论文集(第1册)[C].天津,2001.
[9]汪建华,戚新海.压缩机焊接变形的三维数值模拟[J].机械工程学报,1996,32(1):85-91.
[10]迟哲,刘亚良,王陆钊,等.基于固有应变法的地铁侧墙FSW 焊接变形仿真[J].电焊机,2017,47(10):1-8.
[11]陈婷.搅拌摩擦焊温度场数值模拟研究[D].辽宁:东北大学,2012.
[12]Li T,Shi QY,Li H K.Residual stresses simulation for friction stir welded joint[J].Science&Technology of Welding&Joining,2007,12(8):664-670.
[13]鄢东洋,史清宇,吴爱萍,等.搅拌头机械载荷在搅拌摩擦焊接中的作用的数值分析[J].金属学报,2009,45(8):994-999.
[14]Buffa G,Hua J,Shivpuri R,et al.Design of the friction stir welding tool using the continuum based FEM model[J].Materials Science&Engineering A,2006,419(1-2):381-388.
