刚性淹没球冠状植被水流特性试验研究

赵　芳，Aristotelis　Mavrommatis，Anastasios　Stamou，槐文信，杨中华

（1.武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉　430072；2.中冶南方工程技术有限公司，湖北 武汉　430233；3.雅典国家技术大学 应用水力学实验室，希腊）

1　研究背景

水生植被具有极高的生态服务价值，研究水生植被作用下的水动力特性有助于深入理解植被与水流的相互作用，对于生物多样性的维护、污染物的净化和输移、河湖的生态修复等有着重要意义。越来越多的学者关注并参与到与植被相关的研究中，如淹没植被水流［1-3］、挺水植被水流［4-5］及漂浮植被水流［6-7］，根据植被的柔韧性又可分为刚性植被［8］和柔性植被［9］，植被的存在主要会影响河道水流的流速分布、紊动结构及能量。

流速分布是预测河道过流能力的重要指标，水流流速分布与植被排列方式、植被形状、植被密度、水深等密切相关。对于植被区域充分长且全覆盖河道的水流，大多学者将水流在垂向上进行分层或分区研究。Hsieh和Shiu［10］将淹没植被水流分成了三层，可渗透的土壤层、植被层、自由水层，基于多孔介质理论推导出纵向流速的分析解，植被可以阻碍水流流动并有效防止土壤侵蚀。Huai等［11］在研究刚性淹没植被水流流速的分析解时，沿垂向将水流分为三层：内植被层、外植被层和植被上层，内植被层和植被上层采用混合长度理论求解动量方程，其中植被上层将植被作为边界层修正混合长度，外植被层提出的流速公式含有经验参数，需要大量试验数据进行拟合。刘昭伟等［12］基于混合长度紊流模型得到了表征植被水流垂向流速分布的常微分方程，将灌木植被形态考虑在内，假定灌木直径满足双曲函数，得到了流速的分析解。陈正兵和江春波［13］基于环境流体力学代码（EFDC），代入植被阻力经验公式，分析不同植被密度和植被高度水流的流速和水位，认为滩地种树能明显减小滩地流速并不同程度地抬高主河道水位。Bai等［14］通过试验模拟单个分岔树状植被水流，结果表明横向上尾流发展符合Boussinesq涡黏性规律，纵向上混合长度随着距离的增大而增大，但涡黏性和混合长度在垂向上随高度的增加而减小，这与传统的边界层垂向发展的植被水流研究结果有一定差异，也说明植被形状对河道水流的影响较大。

已有研究成果表明，植被的垂向形状变化对于水流结构有很大的影响。尽管已有不少关于淹没刚性植被水流的研究，但大多数研究都是将刚性植被概化为细圆柱在实验室尺度下进行研究。天然河道中也有许多树状植被，如乔灌木、丁香、紫薇、北海道黄杨、紫叶小檗、腊梅、红王子锦带、红瑞木等景观植物，因此研究树状植被水流是有必要的。本文采用概化的树状植被，旨在研究树状植被影响下的河道水流的水动力特性。

2　实验方法

2.1实验装置实验在雅典国家技术大学应用水力学实验室长16 m，宽0.5 m，高0.5 m的水槽中进行，该水槽底坡为0.001。实验过程中由进口阀门和电磁流量计控制流量，水槽末端安装有可以调节高度的薄壁闸门，用以控制水深，水流可以视为恒定均匀流。

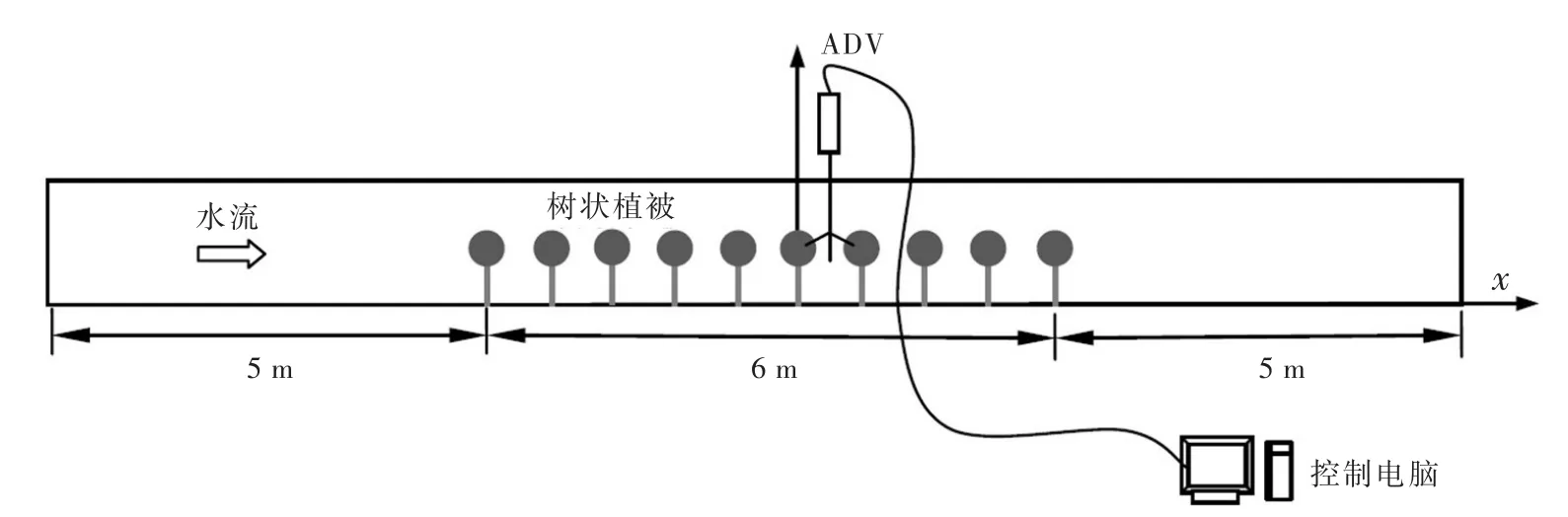
图1　水槽实验设备

实验采用MicroADV（Acoustic Doppler Velocimeter）测量，MicroADV常常被用于实验室尺度的三维流速场的测量，其工作原理基于多普勒效应，当信号由发生器发出，遇到运动中的物体，信号受到反射，而反射回来的声波频率与原信号频率会有一个差值，这个偏差效应被称为多普勒频移效应。ADV探头前端的3个信号接收器朝向交汇于一个区域，即为流速测试区域，测试区域为高5.6 cm，直径4.5 mm的圆柱体。发生器布置在3个探头中间，MicroADV通过发射换能器发出16 MHz频率的3束声波，经过水体的传导，到达距离发射换能器5 cm远的采样点，被水体中的示踪粒子等微粒反射回来，信号被接收传感器收集，通过配套软件计算可得到测试区域内部物体的移动速度与方向。由于MicroADV采样点的空间分辨率为4.5 mm，因此要求采样点距离边壁至少10 mm，为避免采样点与壁面重合，本次实验中近壁区域第一个采样点距水槽底部的最小距离为5 mm，测试值作为参考，第二点距离壁面10 mm。MicroADV的采样频率为25 Hz，各个测点采样时间为120 s，共3000个，以得到流速的时间统计平均值。

树状植被用空心橡胶圆柱和塑料球来模拟（图1），橡胶圆柱直径为6 mm，高5 cm，中间插入长度适中的有机玻璃棒，并固定于水槽底部的插孔内；塑料球直径为3 cm。植被区域长6 m，宽0.5 m，植被间距10 cm×10 cm。植被区域距离水槽最前端和最末端均为5 m。定义x方向为水流方向，y方向为横向，z方向为垂向，坐标原点距植被区前缘4 m，见图2。为了减小水槽边壁对测量的影响且考虑流动充分发展，ADV测量区域位于距植被起始位置下游4 m处的中心位置。垂向测线（图2（b）中灰色点）主要分布在4株植被之间。

2.2实验工况实验共选取了4种较为典型的工况，实验流量为22.42～40.94 L/s，雷诺数为44 533～81 313，弗劳德数为0.115～0.433，为缓流。各工况的实验参数如表1所示，植被密度一定，主要变化流量和水深。

图2　测量区域示意图

表1　各种工况模型参数

3　结果与讨论

3.1平均流速分布

3.1.1纵向流速分布树状植被水流的纵向流速分布不同于常规的圆柱状或是长方体状的植被水流，植被几何形状的改变使得水流结构更加复杂，以工况4为例，根据试验测得的流速数据，经过处理得到了各条测线上无植被与有植被情况的纵向流速的垂向分布图（图3），其中图3（d）为树状植被下游0.5、1、1.5和2 m处的纵向流速的垂向分布，将无植被工况的纵向流速作为参考，无植被工况的纵向流速符合对数率分布，图中点划线表示树冠的上下边界。树冠的存在使得流速在树冠层（z/h=0.625～1）附近减小，主要是由于树干到树冠形状突变造成的。

植株正下游（垂线B）位于树冠植被正后方，受到植被阻力影响最大，在植被层内的纵向流速变化最大，相对其他垂线位置的纵向流速要小得多，在同一横断面（x=5 cm）上，当z/h＜2时，植株正下游（垂线B）的纵向流速最小，垂线A次之；树冠植株空隙中心（垂线C）的纵向流速较大且分布较为均匀，没有在树冠层出现流速突减，但相较于无植被情况，受植被阻力影响，在z/h＜1.5范围内流速减小，z/h＜1.5流速增大。取靠近树冠植被的纵断面（y=2.5 cm）比较垂线A、E、H的纵向流速分布（图3（b）），垂线E、H离树冠植被较近，在树冠顶部以下变化剧烈，相较于垂线A，纵向流速在z/h＜1范围内更小，最小值达/U0=0.15，z/h＜1时流速变化基本一致。在另一纵断面（y=5 cm）比较垂线C、D、F和G的纵向流速分布（图3（c）），垂线D、F、G的纵向流速分布几乎一致，最小流速为/U0=0.35，刚好位于树冠与树干交界处，与树冠植株空隙中心（垂线C）的区别仅仅在z/h=0.625附近流速突减。植被区下游2 m范围内的纵向流速仍受到植被阻力的影响，在z/h＜1.75时，离植被区越远，纵向流速越大。

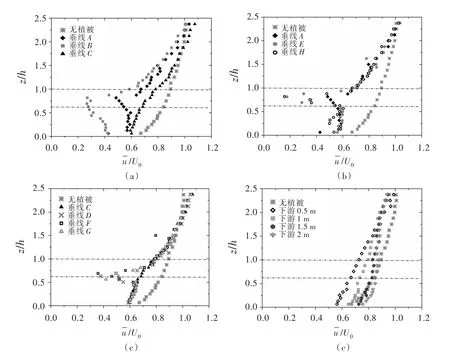
图3　工况4不同位置无量纲纵向流速/U0垂向分布（点划线表示树冠的上下边界）

图4显示了相同植被密度（N=100 m-2）不同流量和水深的树状植被工况在垂线A-D上的纵向流速分布对比。工况1和工况2、工况3和工况4水深相同，流量不同；对于水深H=15.4 cm（z/h=1.925），工况 1的纵向流速/U0在垂线A-D位置稍大于工况 2，说明流量或雷诺数越大，无量纲纵向流速/U0越小，但此关系对于水深H=25 cm（z/h=3.125）已经不明显，工况3和工况4在4个位置处的纵向流速分布基本相同，说明在水深较大时，无量纲的纵向流速的垂向分布规律几乎不受流量和雷诺数的影响。工况1和工况3、工况2和工况4流量相同，水深不同；整体来说，水深越小，纵向流速越大。

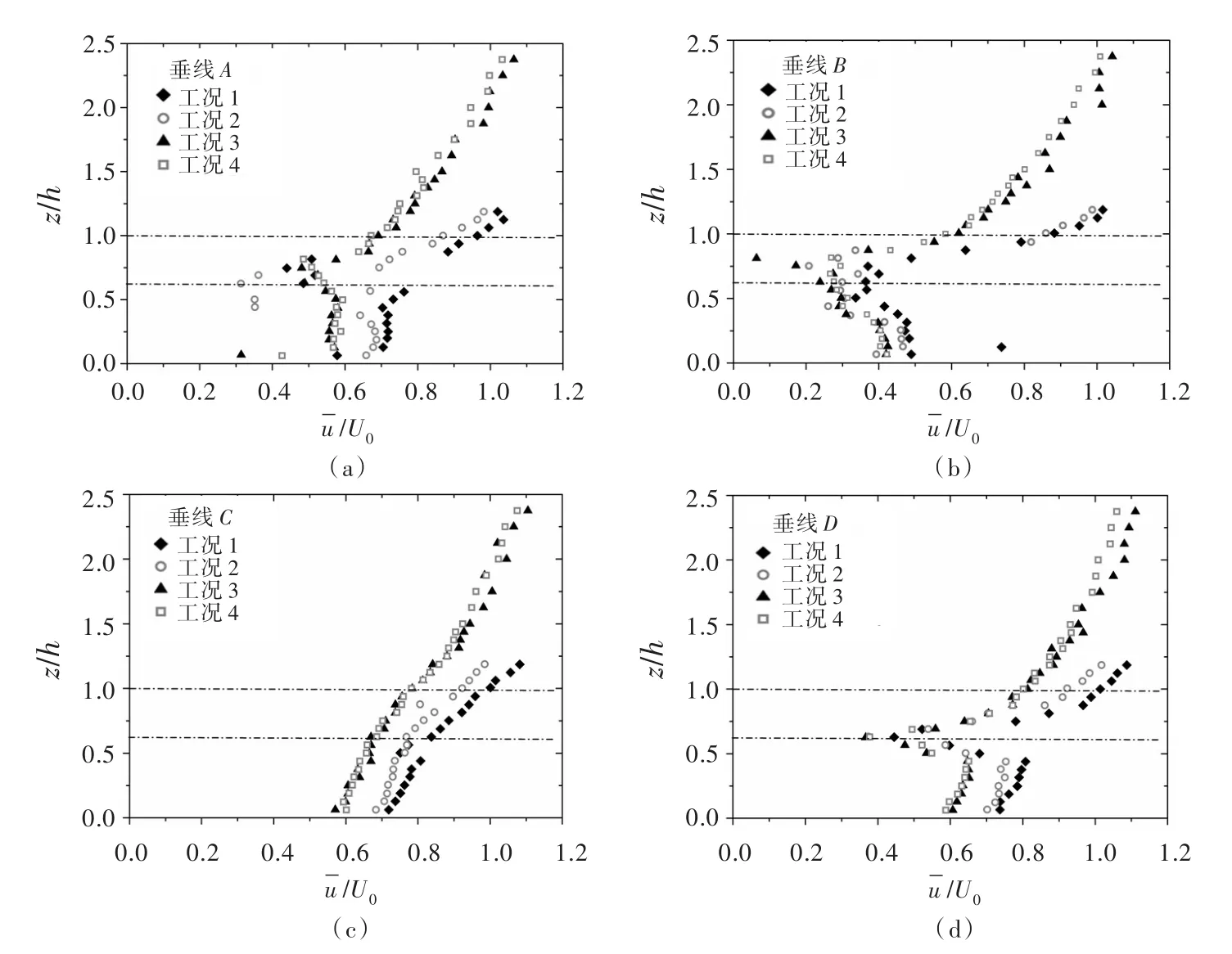
图4　4种工况无量纲纵向流速/U0垂向分布对比

3.1.2垂向流速分布考虑到水流结构受植被形状的影响较大，有必要研究树冠状植被水流的垂向流速变化。主要对比了不同测线位置与无植被情况的垂向流速差异，见图5。其中垂线B的垂向流速变动最大，尤其在树干层树冠层出现负的最大值其次是位于中心断面上的垂线D、F和G，在树冠层垂向流速既有正的最大值也有负的最大值，垂线C的垂向流速变化最小。

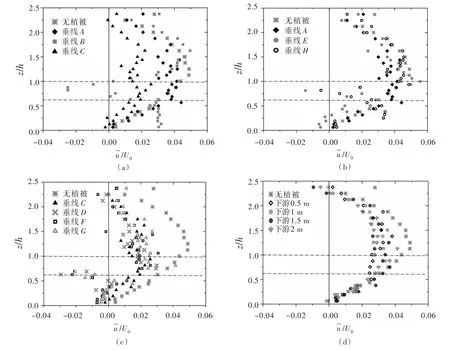
图5　工况4不同位置无量纲垂向流速/U0垂向分布

3.2紊流特性紊动强度的变化对水流中悬浮物、污染物传输有一定影响，因此研究树状植被水流的紊动强度很有必要。紊动强度（urms）是反映水流中流速脉动强弱程度的一个特征值，通常用表示，其中脉动流速为纵向流速，为纵向流速时均值。

工况4的纵向紊动强度在不同垂线位置的变化见图6，所有垂线上的紊动强度均大于无植被情况下的紊动强度，垂线A的紊动强度最大，最大值urms/U0=0.32位于树冠层，植株正下游（垂线B）的紊动强度略大于树冠植株空隙中心（垂线C），植株正下游（垂线B）上紊动强度最大值位于树冠层内，而树冠植株空隙中心（垂线C）的最大值位于树冠顶部稍上位置（z/h=1.1）。垂线E和H上的紊动强度最大值也是位于树冠顶部稍上位置，最大值小于树冠植株空隙中心与植株正下游位置的横向中点位置（垂线A）位置处的紊动强度最大值，在树干层（z/h＜0.625）垂线E和H上的紊动强度大于垂线A的紊动强度。垂线D、F和G的紊动强度最大值位于树冠底部（z/h=0.625），最大值urms/U0=0.2，除了在树冠层靠下位置紊动强度的剧烈变化，垂向上其他位置的紊动强度和树冠植株空隙中心（垂线C）的紊动强度几乎一致。植被区下游4个位置的紊动强度随着距离的增加而减小。

图6　工况4不同位置无量纲纵向流速紊动强度urms/U0垂向分布

3.3紊流结构采用象限分析法研究树冠植被对紊流结构的影响［15-16］。象限分析是将瞬时脉动流速（u′，w′）分布在平面坐标系对应的4个象限Q1、Q2、Q3和Q4内（图7），得到每个象限内对应的雷诺应力贡献值Si，M。第一象限Q1（u′＞0，w′＞0）为外向交互流态；第二象限Q2（u′＜0，w′＞0）为喷射流态；第三象限Q3（u′＜0，w′＜0）为内向交互流态；第四象限Q4（u′＞0，w′＜0）为下扫流态。

通过脉动流速u′，w′与时间的关系（图8），可以很清楚地看到在不同时刻各种流态交替出现，选取工况4垂线C上树冠顶部位置（z/h=1），根据以上流态判别条件，可在图中很明显地看到“喷射”和“下扫”流态。

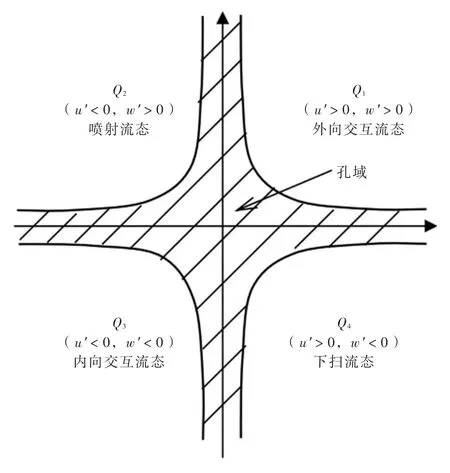
图7　象限分析与孔域示意图

图8　工况4垂线C上z/h=1位置处的脉动流速随时间的变化

Lu和Willmarth［15］在象限分析中定义了“孔域”，见图7阴影部分，孔域是由4条双曲线作为边界围成的区域，其中M为表征孔域大小的参数，在不同阈值参数M下，各流态对雷诺应力的贡献值Si，M可表示为（i=1，2，3，4）：

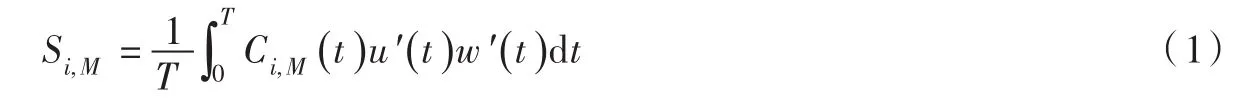
M=0表示将所有的瞬时脉动流速统计起来。图9就为M=0时的象限分析。M常见取值3或4［17］，为极端事件，要求以工况4为例进行分析，将雷诺应力贡献值用植被顶端摩阻流速的平方进行无量纲处理S为水力坡度，0.001；H为水深，h为树冠植被高度，取8 cm。

从图9可以看出，垂线A在树干层（z/h＜0.625）和自由水层（z/h＞1），Q2和Q4占主导，“喷射”和“下扫”流态起主要作用，随着水深增大，“喷射”和“下扫”流态的作用在树干层增大而在自由水层有所减小，在树冠层（0.625＜z/h＜1），Q3“内向交互”的作用也较为明显，很难说明那种流态的作用最大。垂线B在树干层Q1和Q3起主导作用，其作用在树冠下边界（z/h=0.625）尤为明显，在树冠层Q1和Q3的作用减小，Q2和Q4起主导作用，在自由水层依然是Q2和Q4占主导，但Q4的作用略大于Q2，说明在0.625＜z/h＜2.2范围内主要为“下扫”流态。垂线C在整个水深上Q2和Q4占主导，且0＜z/h＜1.5范围内“下扫”流态起主导作用，z/h＞1.5后“喷射”作用占主导。垂线D的紊动结构在树干层和自由水层中Q2和Q4起主导作用，在树冠层的大部分区域Q2和Q4占优。

总体来说，下扫作用主要在植被层占主导，喷射作用主要在自由水层占主导，两种作用转化的临界点位于树冠植被上方；位于植被正后方的位置较为特殊，在树干层内内向交互和外向交互作用占优，树干层以上下扫和喷射起主导作用。

4　结论

通过对淹没树冠状植被水流水动力学特性的实验研究，可以得出以下结论：

（1）受树冠状植被的影响，水流结构较为复杂。除了树冠植株空隙中心（垂线C）附近，纵向流速分布在树冠层先减小后增大，垂向流速也在树冠层附近剧烈变化；位于植株正下游（垂线B）的纵向流速最小，树冠植株空隙中心与植株正下游位置的横向中点位置（垂线A）次之，树冠植株空隙中心的纵向流速较大且分布较为均匀，没有在树冠层出现流速减小；在相同流量条件下，水深越小，纵向流速越大。

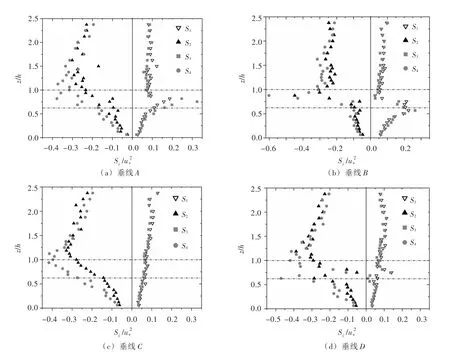
图9　工况4在不同垂线处的象限分析

（2）相对于无植被情况下的紊动强度，树冠植被区域的紊动强度较大；树冠植株空隙中心与植株正下游位置的横向中点位置（垂线A）的紊动强度最大，植株正下游（垂线B）的紊动强度次之，且紊动强度最大值位于树冠层，而树冠植株空隙中心（垂线C）的最大值位于树冠顶部稍上位置；垂线E和H上的紊动强度最大值也是位于树冠顶部稍上位置，最大值小于树冠植株空隙中心与植株正下游位置的横向中点位置处的紊动强度最大值，在树干层（z/h＜0.625）垂线E和H上的紊动强度大于树冠植株空隙中心与植株正下游位置的横向中点位置（垂线A）的紊动强度。

（3）通过象限分析研究树冠植被水流的紊流结构，下扫流态主要在植被层占主导，喷射流态主要在自由水层占主导，两种流态转化的临界点位于树冠植被上方；位于植被正下游的位置较为特殊，在树干层内内向交互和外向交互作用占优，树干层以上下扫和喷射起主导作用。

参考文献：

［1］GHISALBERTI M，NEPF H M.Mixing layers and coherent structures in vegetated aquatic flows［J］.Journal of Geophysical Research，2002，107（C2）：3011.

［2］POGGI D，PORPORATO A，RIDOLFI L，et al.The effect of vegetation density on canopy sub-layer turbulence［J］.Boundary-Layer Meteorology，2004，111（3）：565-587.

［3 ］NEZU I，SANJOU M.Turburence structure and coherent motion in vegetated canopy open-channel flows［J］.Journal of Hydro-environment Research，2008，2（2）：62-90.

［4］TANINO Y，NEPF H M.Laboratory investigation of mean drag in a random array of rigid，emergent cylinders［J］.Journal of Hydraulic Engineering，2008，134（1）：34-41.

［5］AUGUSTIN L N，IRISH J L，LYNETT P.Laboratory and numerical studies of wave damping by emergent and near-emergent wetland vegetation［J］.Coastal Engineering，2009，56（3）：332-340.

［6 ］PLEW D R.Depth-averaged drag coefficient for modeling flow through suspended canopies［J］.Journal of Hydraulic Engineering，2011，137（2）：234-247.

［7］HUAI W，HU Y，ZENG Y，et al.Velocity distribution for open channel flows with suspended vegetation［J］.Advances in Water Resources，2012，49（8）：56-61.

［8］赵芳，槐文信，胡阳，等.双层刚性植被明渠水流特性实验研究［J］.华中科技大学学报（自然科学版），2015，43（1）：85-90.

［9］槐文信，唐雪，王伟杰.柔性淹没植被对生态河道洪水波影响研究［J］.华中科技大学学报（自然科学版），2016，44（4）：111-115.

［10］HSIEH P C，SHIU Y S.Analytical solutions for water flow passing over a vegetal area［J］.Advances in Water Resources，2006，29（9）：1257-1266.

［11］HUAI W X，ZENG Y H，XU Z G，et al.Three-layer model for vertical velocity distribution in open channel flow with submerged rigid vegetation［J］.Advances in Water Resources，2009，32（4）：487-492.

［12］刘昭伟，陈永灿，朱德军，等.灌木植被水流的流速垂向分布.水力发电学报，2011，30（6）：237-241.

［13］陈正兵，江春波.滩地植被对河道水流影响［J］.清华大学学报（自然科学版），2012，52（6）：804-808.

［14］BAI K，MENEVEAU C，KATZ J.Near-wake turbulent flow structure and mixing length downstream of a fractal tree［J］.Boundary-layer Meteorology，2012，143（2）：285-308.

［15］LU S S，WILLMARTH W W.Measurements of the structure of the Reynolds stress in a turbulent boundary layer［J］.Journal of Fluid Mechanics，1973，60（3）：481-511.

［16］张英豪，赖锡军，姜加虎.含苦草水流紊流结构典型剖面的象限分析［J］.水动力学研究与进展（A辑），2015，30（5）：526-532.

［17］POGGI D，PORPORATO A，RIDOLFI L，et al.The effect of vegetation density on canopy sub-layer turbulence［J］.Boundary-Layer Meteorology，2004，111（3）：565-587.