洪家渡水电站厂房后高边坡变形特征研究
2018-04-17
(中国电建集团贵阳勘测设计研究院有限公司,贵州 贵阳 550081)
岩石高边坡是山区工程建设中的主要地质环境和工程承载体,其稳定性决定着工程全生命周期的安全和效益。人工边坡的破坏失稳一般在其变形发展到一定程度后发生,因此对坡体的变形进行监测,了解其变化规律,可在边坡发生失稳破坏前采取有效的工程处理措施,确保安全。
本文以洪家渡水电站厂房后高边坡近15年的变形观测数据为基础,结合工程地质情况,全面分析该高边坡变形特征,采用数理统计的方法建立边坡变形统计回归模型,定量分析影响边坡变形的各因子权值,可判断边坡稳定和预测边坡变形趋势。
1 工程概况
1.1 工程地质及开挖支护简介
厂房后高边坡开口线高程为1025.00~1070.00m,开挖高20~75m,每层开挖高13m。高程1036.00m以上开挖坡比1∶0.45~1∶0.65,以下为垂直开挖。
边坡开挖出露地层为玉龙山段T1y2-5~T1y2-4厚层、中厚层微~新鲜灰岩;顶部出露部分九级滩段T1y3-1泥灰岩夹页岩及第四系残坡积的碎块石夹少量黏土。边坡岩层N70°~75°E,NW∠28°~31°,为斜顺向或逆向坡。发育裂隙共89条,其中最为发育的一组裂隙产状N50°~70°E,SE∠60°~75°,充填方解石及泥质,剪性。主要断层有F8、F13,其中F8为正断层,斜穿下游侧坡,产状N80°E,SE∠50°,破碎带宽1~3m,影响带宽3~5m,断层带溶蚀破碎严重,且发育溶洞;F13为逆断层,斜穿下游侧坡,于高程1036.00~1049.00m边坡交汇,产状N55°E,NW∠40o,破碎带宽0.5~1.5m,影响带宽2~5m,断层带局部溶蚀破碎严重。断层带及溶洞周边裂隙发育,岩体破碎。典型地质剖面如图1所示。

图1 边坡典型地质剖面
厂房开挖边坡为斜顺向或逆向坡,且发育的F8断层均与坡体呈大角度相交,边坡整体稳定性较好,但坡体裂隙较为发育,特别是受N40°~60°W,SW∠55°~75°组裂隙(该组裂隙与坡体倾向基本一致)与其他结构面切割的影响,边坡多处存在不稳定体。同时,下游侧坡风化溶蚀较严重,溶洞发育。因此为保证厂房开挖边坡安全,采取的工程处理措施为
a.对边坡松动块体进行清除,危岩体采用随机锚杆进行加固。
b.对边坡均进行系统锚杆、挂网喷混凝土支护,大部分边坡进行钢筋混凝土护坡。
c.规模较小的溶洞(其发育深度小于5m)若存在充填物时,首先清除充填物后再采用混凝土回填,空腔溶洞直接用混凝土回填;对于规模较大的溶洞,回填水平深度3~8m,并清除回填段内充填物,溶洞周边布设锚杆进行加固后用混凝土回填。
d.对残缺马道均用混凝土进行修复。
e.在高程997.20m、高程1025.00m处设置两层排水洞对坡体进行排水处理。
1.2 监测布置
根据《水利水电工程边坡设计规范》(SL 386—2007)和《土石坝安全监测技术规范》(DL/T5259—2010)规定:厂房后开挖所形成的边坡为1级,其内部变形为永久监测项目。因此,在厂横0-016.00、A—A断面、厂纵0-004.50、厂纵0+013.68这四个断面布置多点位移计对边坡沿深度方向的水平位移进行长期监测,判断边坡位移深度。监测仪器分布统计见表1,空间位置如图2所示。
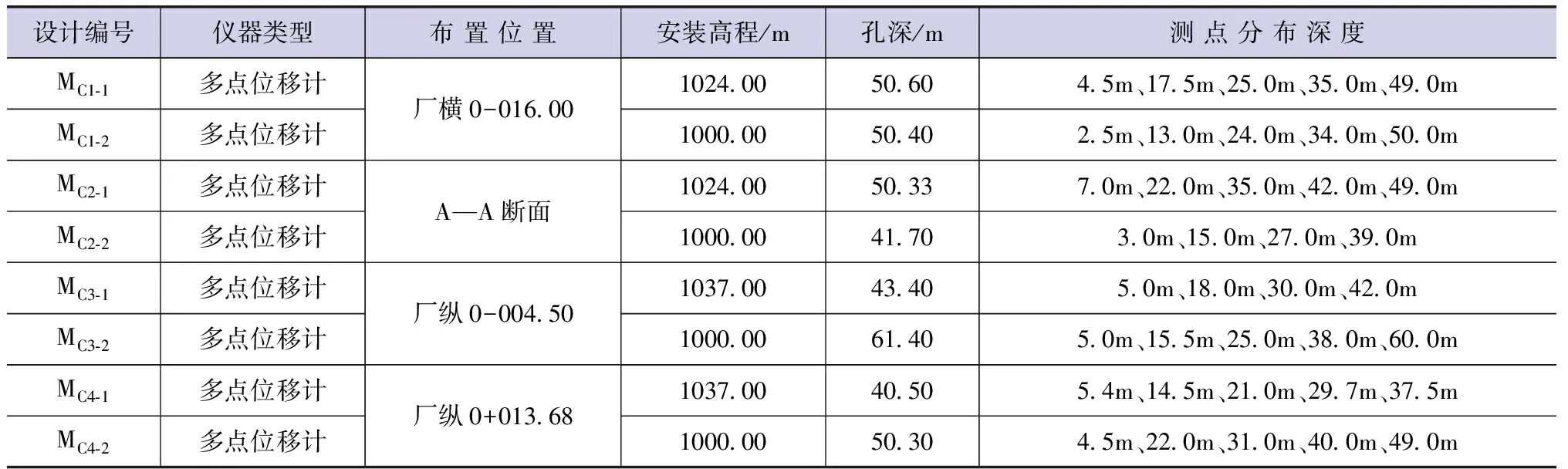
表1 厂房后高边坡监测仪器

图2 厂房后高边坡监测布置
2 边坡变形特征分析
2.1 厂横0-016.00剖面
由图3、图4可知:MC1-1、MC1-2各深度测点位移未与降雨量呈现一定的相关性变化,即在每年降雨量较多的5—8月期间及短期暴雨前后,边坡位移未见趋势性变化。
边坡历史最大位移均发生在浅表层,且多发生在施工开挖阶段,随着时间的推移,各测点位移呈周期性波动变化,目前已处于稳定状态。
2.2 A—A剖面
由图5、图6可知:MC2-1、MC2-2各深度测点位移量值不大,且未与降雨量呈现一定的相关性变化。
边坡历史最大位移均发生在浅表层,且多发生在施工开挖阶段。其中MC2-1各深度处测点位移在支护完成后基本保持不变;MC2-2监测历史最大位移1.80mm,最大位移接近其多年位移平均值,表明位移波动幅度较小,测值稳定。各深度处测点位移在2012年之前均呈现周期性波动的缓慢增大趋势,之后则基本呈现较为稳定的周期性波动变化,规律性较好,位移已基本收敛。
2.3 厂纵0-004.50剖面
由图7可知:MC3-1监测历史最大位移3.42mm,发生在孔口处,最大位移接近其多年位移平均值,表明位移波动幅度较小,其余各测点位移均不大,未见明显异常变化。各测点位移主要发生在开挖前期,随着时间推移,各测点位移均呈现周期性波动变化,规律性较好,已基本收敛。

图3 多点位移计位移MC1-1位移与降雨量变化过程线

图4 多点位移计MC1-2位移与降雨量变化过程线

图5 多点位移计MC2-1位移与降雨量变化过程线
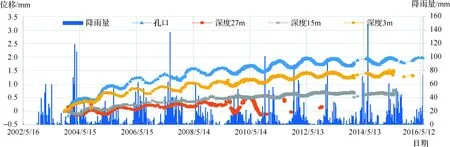
图6 多点位移计MC2-2位移与降雨量变化过程线

图7 多点位移计MC3-1位移与降雨量变化过程线
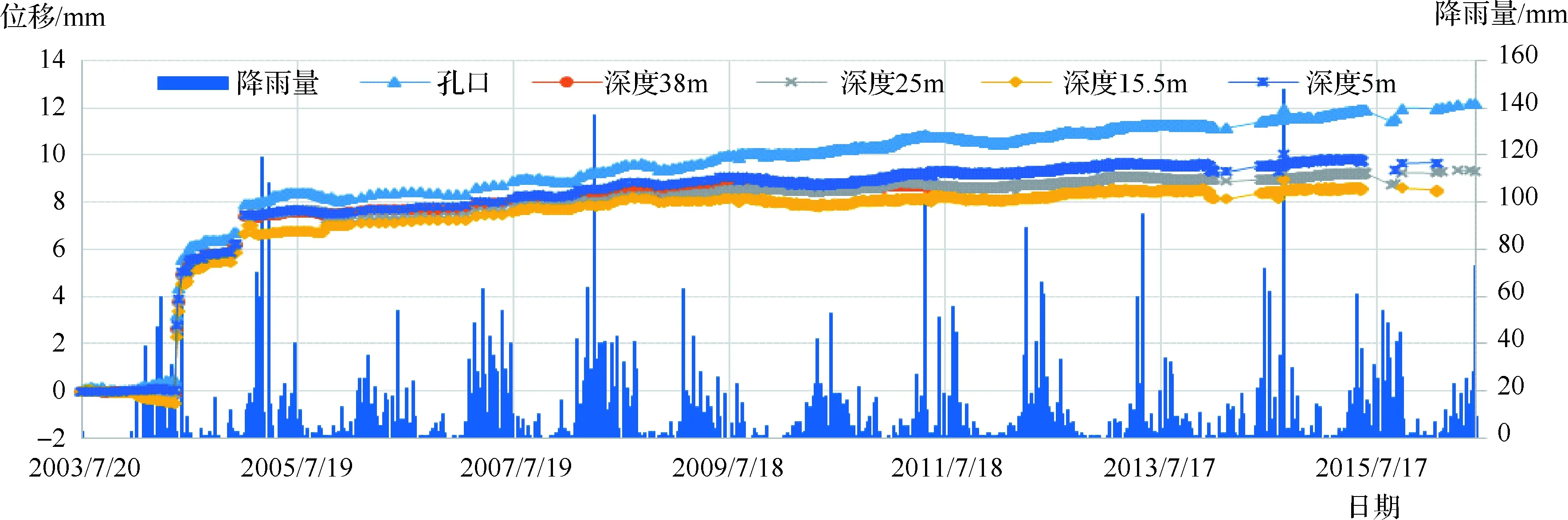
图8 多点位移计MC3-2位移与降雨量变化过程线
由图8可知:MC3-2监测历史最大位移12.18mm,发生在孔口处。各测点历史实测位移的量值均明显大于同断面高程处MC3-1各测点位移,但位移主要由施工期开挖引起,开挖期间所发生的位移均接近8mm。随着时间推移,各测点位移变化趋缓,但均呈现缓慢增大趋势,且孔口处位移变化速率略大于其他各深度处测点位移速率。从2005年至今,各测点年变化速率分别为0.344mm/a、0.153mm/a、0.150mm/a、0.180mm/a。该套多点位移计穿过断层F8,该断层溶蚀破碎严重,是导致多点位移计出现缓慢变形的主要原因。
另外,各深度测点位移亦未与降雨量呈现相关性变化。
2.4 厂纵0+013.68剖面
由图9可知:MC4-1各深度处测点实测位移在2011年5月之前基本趋于稳定,之后缓慢启动第二次位移过程,至2013年11月份开始出现明显增大趋势,变形速率增大。从2013年至今,各测点年变化速率分别为0.234mm/a、0.114mm/a、0.154mm/a、0.134mm/a、0.074mm/a。同时,各深度测点位移与降雨量呈现微弱的相关性,即在短期降雨量较为集中以及暴雨前后有小幅增大,但滞后明显。分析原因主要为该段边坡两面临空,且岩溶发育,岩体完整性差,从而引起坡体产生蠕变变形。
由图10可知:MC4-2仅孔口处测点位移呈现缓慢增大趋势,近几年年变化速率为0.222mm/a。其余各测点实测位移变化平缓,基本收敛,其中位于22m和31m深度处的测点实测位移未见收敛,且与孔口处位移方向相反,而位于4.5m深度处的位移基本不变,表明在深度4.5~22m区间内可能存在破裂面。同时,各深度测点位移与降雨量未呈现明显的相关性。

图9 多点位移计MC4-1位移与降雨量变化过程线

图10 多点位移计MC4-2位移与降雨量变化过程线
3 边坡变形模型建立及成果分析
3.1 模型建立
大量工程表明,温度、降雨量与边坡变形存在一定的相关性,时效也将对边坡变形产生一定影响。因此综合考虑温度、降雨量和时效三个因素影响,边坡变形统计模型可表示为
δ=δT+δP+δθ
(1)
式中δ——位移量因子,mm;
δT——温度分量因子;
δP——降雨量分量因子;
δθ——时效分量因子。
3.1.1温度分量
从多年观测资料来看,坝址气温基本上呈年周期性变化,温度因子可选用周期的谐波作为因子,由此求得温度分量δT如下:
(2)
式中ai——回归系数(i=1~4);
t——监测日至始测日的累计天数/d。
3.1.2降雨量分量
降雨对边坡位移的影响具有一定滞后作用,影响时段一般在15d以内,因此采用前期平均降雨量作为影响因子:
(3)
式中Pm——前m天平均降雨量,m为1、3、5、15,mm;
bj——降雨量变化引起位移分量的回归系数。
3.1.3时效分量
边坡产生时效变形的原因极为复杂,参照类似工程经验,采用式(4)来表示位移变化的时效分量,即
δθ=c1θ+c2lnθ
(4)
式中θ——累计观测天数除以100的值;
c1、c2——时效分量的回归系数。
3.2 成果分析
根据监测成果可知,边坡位移主要发生在浅表层,因此选取多点位移计浅层实测位移资料进行回归分析,成果见表2和表3。
由表2可知:边坡变形回归模型总体精度较高,拟合复相关系数介于0.90~0.97(除MC4-1),基本能够反映边坡变形的真实情况。
由表3可知:各影响因子在边坡变形中的贡献依次为:坝址气温>时效>降雨量,表明坝址气温和时效为引起边坡变形的主要因素,降雨量的影响微弱。
目前坝址气温呈年周期性变化,降雨量也呈较好的正态分布特征,各年度内的变幅相近,而时效因子呈增大趋势。因此,时效变形是引起边坡蠕变的主要原因。
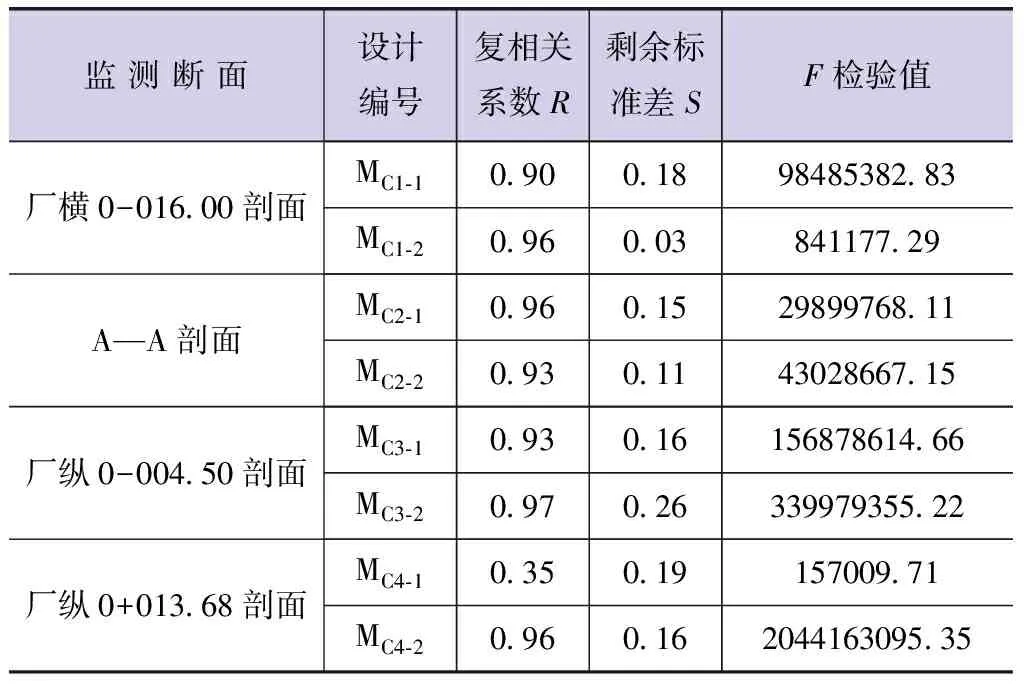
表2 拟合成果检验

表3 拟 合 成 果
4 结 论
a.厂房后高边坡历史位移量值均不大,且主要发生于浅表层,各部位坡体位移的年变化速率介于0.074~0.344mm/a,变化速率小。目前边坡总体处于稳定状态,其中正后方边坡已稳定,侧方边坡靠近河道的区段,由于边坡两面临空,岩溶发育,岩体较破碎,岩体完整性差,坡体存在蠕变变形。
b.建立的边坡变形回归模型精度较好,测点拟合复相关系数介于0.90~0.97,拟合成果表明坝址气温和时效变形对坡体浅层位移影响最大,降雨量的影响微弱,与实际监测成果吻合。该模型可作为判断边坡稳定和预测边坡变形趋势的有效手段之一。
c.在该模型的基础上,后续可根据边坡长序列的观测数据不断更新调整模型,以确保其长期回归预测结果的精准。
[1]陈兰,仲云飞,吴邦彬,等.逐步回归算法在边坡安全监测中的运用[J].长江科学院院报,2013(1):21-25.
[2]谈小龙,徐卫亚,刘大文,等.高边坡变形的组合预测模型及其应用[J].水利学报,2010(3):294-299.
[3]刘海洋,郝哲.基于时序分析的边坡变形预报与变形行为特征[J].沈阳大学学报(自然科学版),2012(2):81-86.
