梁的独立覆盖分析方法

,

(长江科学院 材料与结构研究所，武汉　430010)

1　研究背景

梁、板、壳是工程结构中的常见形式，其特点是结构不同方向的尺寸差别较大，比如梁的长度远大于其他方向的尺寸。最初的梁板壳力学分析是根据材料力学和弹性力学的经典解，但只适用于简单结构形式及边界条件。随着计算技术的发展，以有限元法为代表的数值计算方法，因其能处理任意复杂的结构形式和边界条件而成为梁板壳分析的主要方法。作为有限元法的经典著作，文献[1]对梁板壳问题有如下描述：梁、板和壳仅仅是三维实体的一种特殊形式，至少对于弹性问题而言，处理起来并没有理论上的困难，但这类结构的厚度与其他尺度相比非常小，完全三维的数值处理方式不仅使计算代价过高，而且还经常会导致严重的数值病态问题。

因此，通常的梁板壳分析基于2个基本假设：①垂直于中面的横截面，在变形过程中始终保持为平面(支撑点和集中荷载作用点附近除外)；②沿厚度方向产生的直接应变可以忽略。由此推导出不同于实体分析的控制方程，并发展了各种梁板壳有限单元类型，但其中一些问题有一定的复杂性，直至今日还在研究。

考虑到梁是三者中具有代表性的基本模型，本文以二维梁(单位宽度的矩形截面梁)为例进行讨论，但本质上是着眼于梁板壳类问题的一般性方法。这里参考文献[1]和[2]，将梁(进一步引申至板壳)的分析思路及主要存在的问题归纳如下。

(1)Euler-Bernoulli梁理论。在基本假设的基础上再引入“直法线假设”——变形后的截面仍垂直于中面，适用于细长梁(截面尺寸h与梁长l之比很小)，忽略剪应变。这是经典的梁弯曲理论，对应于薄板壳的Kirchhoff理论，都是求解以挠度为未知量的4阶微分方程，在理论上要求插值函数满足C1连续性，处理起来远比仅要求C0连续性的实体单元复杂，这是梁板壳分析的主要难点(也是相关研究的主推力)。虽然采用Hermite插值函数构造C1梁单元并无困难，但构造C1板壳单元却相当棘手，因而从有限元法最早发展开始，就有大量研究投入其中。文献[1]和[2]介绍了各种方案，但都有各自的问题：协调板单元往往过于刚硬，而且总的来说位移函数比较复杂；非协调方式相对简单，比如仅在结点上保持C1连续，但要进行“分片检验”以保证收敛性，而有些单元只在特殊的网格形式下才能通过“分片检验”。另外，梁板壳单元与实体单元的连接一般需要特殊的技巧。

(2)Timoshenko梁理论。仅考虑基本假设，变形后的横截面不一定垂直于中面，适用于粗短梁(h与l之比并非很小)，考虑剪应变。其对应于厚板壳的Reissner-Mindlin理论，挠度和转角独立插值，将C1连续简化为C0连续。然而退化到求解细长梁或薄板壳时会出现剪切自锁，虽然可以采用减缩积分的措施，但又可能遇到奇异性问题。同时，通常采用的线性单元缺乏描述纯弯曲状态的能力，收敛很慢。

还有采用其他的变分原理或杂交元等方式。综上所述，梁板壳吸引着不少研究者应用各种数学、力学知识和技巧，从而产生出非常丰富的研究成果，而使用者也常常面临着采用“哪个单元”的困惑。

本文采用基于独立覆盖的数值流形方法(简称独立覆盖流形法)，提出梁的独立覆盖分析方法，几乎可以避免现有方法的所有问题。以下首先简要介绍独立覆盖流形法的基本思想，然后分别采用完全多项式、独立的挠度和转角、非独立转角的3种近似场函数定义方式，相应地实现梁的实体分析、Timoshenko梁、Euler-Bernoulli梁，并给出考虑局部坐标系的独立覆盖流形法公式和具体的积分方法，为梁板壳分析提供全新的解决方案。

2　独立覆盖流形法简介

2012年，笔者在石根华博士的建议下，在流形法中首次引入“独立覆盖”[6-7]，即单位分解函数φi=1、近似函数V就是给定级数Vi的覆盖区域;独立覆盖之间为窄条形(三维为窄带状)的覆盖重叠区域，其单位分解函数取为有限元线性形函数以实现覆盖函数的线性过渡。首先研究了矩形独立覆盖。2013年提出任意形状的独立覆盖[8]，如图1所示，3个任意形状的独立覆盖用条形(包括条形交叉处的过渡单元)连接，这样，覆盖的划分不仅能适应求解域的物理边界，还能严格施加本质边界条件(而一般的流形法采用硬弹簧施加边界条件)。比如，将图2所示的细长曲梁划分为4个独立覆盖，其间用条形相连，在梁的两端通过条形与定义了边界条件的结点相连。2015年笔者在文献[9]中正式命名“基于独立覆盖的数值流形方法”，其中，独立覆盖和条形都是基本的计算单元(或称为覆盖网格)，但强调独立覆盖的主体作用。

图1　任意形状的独立覆盖及其条形连接Fig．1　Independentcoverswitharbitraryshapeconnectedthroughstrips图2　曲梁的独立覆盖划分及其条形连接Fig．2　Acurvedbeamdividedbyindependentcoversconnectedthroughstrips

3　梁的独立覆盖函数

暂且设梁的长度和厚度方向分别沿着整体坐标系的x和y轴，如图3所示。本节给出完全多项式、独立的挠度和转角、非独立转角的独立覆盖函数，这些近似函数不限于描述纯弯曲变形，而是包含轴向的更一般的变形。

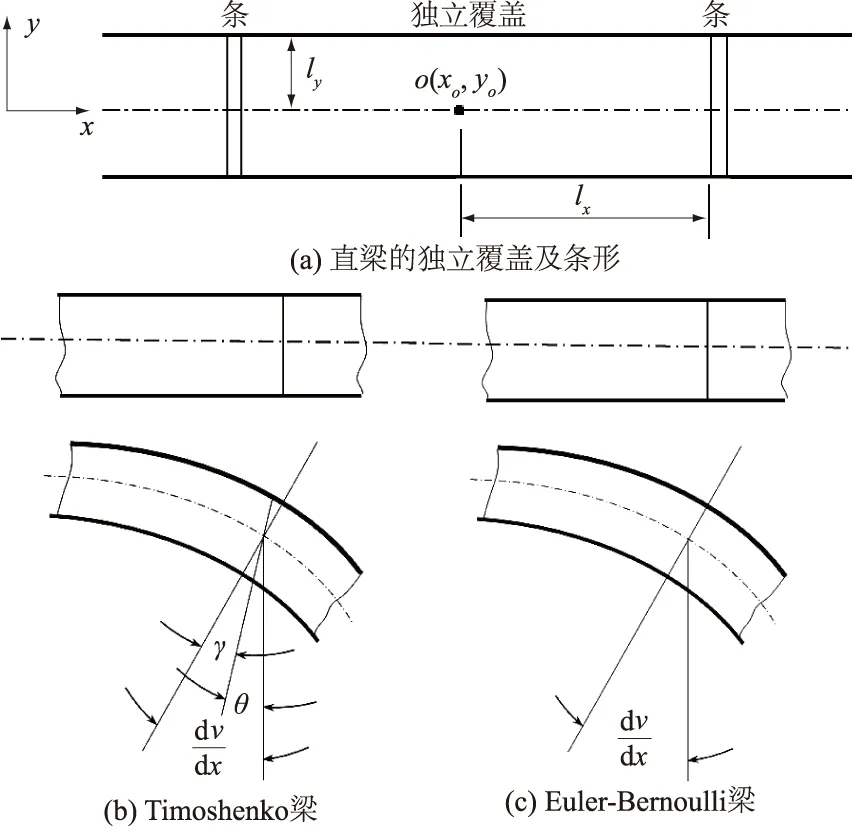
图3　整体坐标系下的直梁及其变形Fig.3　Straight beams and their deformation underthe global coordinate system

3.1　实体分析——完全多项式的覆盖函数

将梁作为二维实体，在独立覆盖中，设x和y方向的位移分别为u和v，采用完全多项式表示为

(1)

式中:ank,bnk为待求的多项式系数;p为设定的多项式最高阶次。图4显示了从0阶到3阶的完全多项式，单个方向上总的项数为p(p+1)/2。

(a) 长度方向

(b) 厚度方向

图4多项式列表
Fig.4Polynomialsmatrix

每个单项式f(x,y)=xn-kyk，而在实际计算中将其替换为做了归一化处理的局部表达式为

(2)

从而避免了将梁作为实体计算时可能出现的数值病态，其中，(x0，y0)取为该独立覆盖的梁中心坐标，lx和ly分别表示2个方向的尺度，lx可取为长度方向的覆盖大小的一半，ly取其平均厚度的一半，如图3(a)所示。以下为方便起见，仍表述为f(x,y)=xn-kyk的形式。

3.2　Timoshenko梁——考虑基本假设的覆盖函数

如图3(b)所示的梁的变形形态，参考文献[1]，设

(3)

式中:根据基本假设(2)——沿厚度y方向的变化可忽略，设梁中面两方向位移分别为f1(x)和f3(x)，则在截面上，梁的挠度保持为f3(x)；再根据基本假设(1)，用yf2(x)描述水平向纤维沿厚度方向呈线性变化的伸长量，其中f2(x)代表独立定义的截面转角θ，它与变形后的垂直截面转角dv/dx的差别为剪应变γ。

如图4所示，在实体计算的基础上，只需考虑多项式列表中的虚线左侧的各单项式，而将虚线右侧的各单项式所对应的自由度约束，使其不参与计算，就能很容易地实现式(3)，其中：f1(x)和yf2(x)分别对应于长度列表中沿虚线方向的第1排(1，x，x2，…)和第2排(y，xy，x2y，…)，f3(x)对应于厚度列表中虚线左侧的一排。

从图4还可看出，当u和v取同阶多项式时，v=f3(x)比θ=f2(x)高1阶。而在有限元法中，Timoshenko梁单元在处理细长梁所遇到的剪切自锁来源于挠度和转角的阶次相同，其解决方案多是基于使挠度高于转角1次的考虑[2]。因此，本文方法自动避免了剪切自锁问题。另外建议阶次p≥2，就能解决有限元法的线性单元难以描述纯弯曲的问题。

3.3　Euler-Bernoulli梁——考虑“直法线假设”的覆盖函数

如图3(c)所示，设截面转角θ=dv/dx=f′3(x)，进一步将图4长度列表中的虚线左侧一排的自由度约束，则由式(4)模拟出“直法线假设”。

(4)

式(4)暗含着保持f3(x)导数连续性的要求，然而在独立覆盖和条形之间的界面上，导数一般是不连续的，存在不协调问题，而且造成在条形内也不能严格满足式(4)。笔者在文献[9]中指出独立覆盖流形法的一大特点：随着覆盖函数阶次的提高，近似场函数的导数趋向于连续的真实解，具有收敛性。因此与文献[1]介绍的能通过“分片检验”的多种非协调单元一样，本文方法也是收敛的。

综上所述，本文方法可完全采用实体计算方式，应用实体计算程序直接求解，而且仅需去掉一些自由度就可以模拟出梁的假设。考虑到梁板壳分析的特殊性，还需要引入局部坐标系，在局部坐标下同样采用上述方式约束一些自由度。

图5　局部坐标系下的梁的独立覆盖Fig.5　Independent covers on beams under the localcoordinate systems

4　局部坐标系下的独立覆盖流形法公式

如图5(a)和图5(b)所示，以相邻的2个独立覆盖为例。在第i(i=1，2)个独立覆盖内，以梁中面的中点(x0i，y0i)为原点建立局部坐标系xi-yi，xi轴与整体坐标x轴的夹角为αi。

对于第3节中的方式(1)——实体分析和方式(2)——Timoshenko梁，局部坐标系下的独立覆盖位移统一表示为

(5)

式中:pi为该独立覆盖所取的多项式最高阶次;Nink和dink分别为对应于某个单项式的覆盖函数矩阵和待求未知量列阵。式中的xi和yi相当于式(2)中的x-x0和y-y0，只需再除以常数lx和ly的幂次就可以实现单项式的局部表达。

引入转换矩阵Li，转换到整体坐标系下的位移,即

(6)

如图5所示，在独立覆盖1和独立覆盖2的条形重叠区域,有

(7)

式中w1和w2是对应于2个覆盖的单位分解函数，取为梁中面上A，B两点之间的一维有限单元的线性形函数[2]，由A,B两点的整体坐标确定,m=2。显而易见，只需考虑i=1并令wi=1，式(7)就成为独立覆盖内的位移表达式(6)。因此不失一般性，以下公式都在条形区域内推导。

(8)

(9)

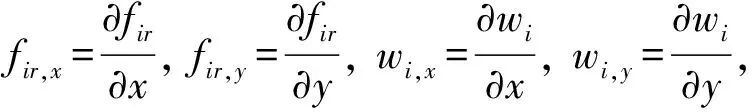
(10)

其中:

(11)

考虑局部坐标和整体坐标的转换,即

(12)

则有:

(13)

对于本文主要讨论的单位宽度的矩形截面梁，单元刚度矩阵的子矩阵为

(14)

式中：Ω为计算单元的区域；r，s依次对第1个和第2个多项式覆盖函数的所有项进行循环;D为平面应力的弹性矩阵,其表达式为

(15)

(16)

分布荷载的子向量为

(17)

式中:qxi和qyi分别为水平向和竖向的荷载集度;l为分布荷载的作用线。集中荷载类似。

对于第3节中的式(3)——Euler-Bernoulli梁，按照式(4)去掉多项式的某些项，覆盖函数实际表示为

(18)

应变矩阵、刚度矩阵和荷载向量的推导类似，具体过程从略。

图6　局部坐标下梁的独立覆盖及其连接Fig.6　Independent coverson beams under the localcoordinate systems

将上述单元刚度矩阵和荷载向量组集成整体刚度矩阵和荷载向量，然后加上边界条件，就可以求解线性方程组得到多项式的系数。本文暂时只考虑全约束的边界条件。可以采用流形法一般使用的硬弹簧的施加方式，或者用条形与边界结点相连实现边界条件的严格施加。后者如图6所示，如果要在梁的一端(C截面)施加位移和转角的全约束，则在C结点处定义局部坐标系x1-y1(也可与整体坐标系一致)和结点覆盖函数，C结点与相邻独立覆盖之间的条形参与计算，但C结点的部分自由度不计入整体自由度。具体处理方法以及其他边界条件情况见文献[10]。

5　积分方法

若计算单元内的材料参数为常数，则式(16)中的被积函数就只需考虑fir,xfjs,x等4项。以fir,xfjs,x为例，有

(19)

5.1　实体积分

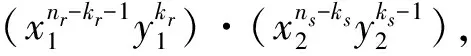
对于梁板壳这样在厚度方向尺寸很小的特殊结构，还可采用特殊的积分方式。以下首先针对本文主要讨论的单位宽度的矩形截面梁，在每个独立覆盖、或直梁上的条形区域内，给出简化的一维积分公式，然后讨论更一般的积分方式。

5.2　一维积分公式

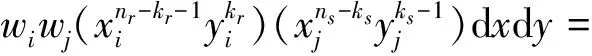
(20)

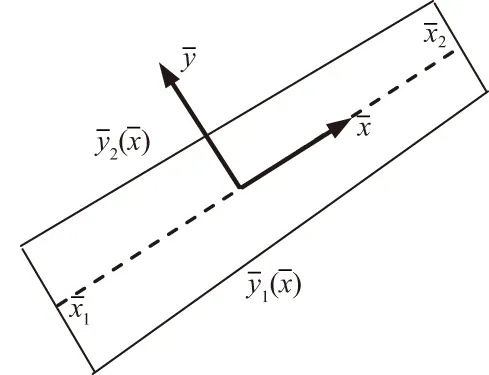
图7　局部坐标系下梁的计算单元Fig.7　 An element onthe beam under the localcoordinate system

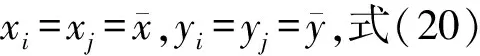
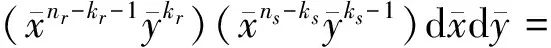
(21)

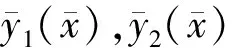
5.3　一般的积分思路

综上所述，本文给出的适应于梁这种特殊结构的积分思路是：先沿截面积分、再沿轴向积分，其中对于复杂截面，前者也可采用数值积分方式。这种方法也为多层复合材料以及非线性本构的模拟提供了条件。

6　算　例

6.1　矩形截面梁受分布荷载作用

如图8所示左端固定的悬臂梁，梁长10 m，截面尺寸为1 m。梁的弹性模量E=300 000 kN/m2，泊松比μ=0。在上表面承受线性分布的横向荷载，集度为：x=0 m处1 kN/m，x=10 m处0 kN/m。划分为5个独立覆盖。

图8　承受线性分布荷载的悬臂梁Fig.8　A cantilever beam subjected to a uniformdistributed load

本算例采用实体计算程序，包括实体积分方式和硬弹簧约束方式，仅仅在独立覆盖函数的选取上按第3节的方法分别实现实体分析、Timoshenko梁和Euler-Bernoulli梁。采用3阶多项式，自由端的挠度见表1，梁上表面的水平向应力见图9，均与材料力学解[12]符合得很好。表中同时给出了各种计算方式的自由度以及采用同一迭代求解器[13]及同一收敛标准的方程组迭代次数，可见，相对于完全实体的计算方式而言，Timoshenko梁和Euler-Bernoulli梁引入了假设，计算量大幅下降(考虑自由度和方程迭代次数的减少)，本例在3阶情况下的计算量分别小于实体分析的30%和20%。

表1　梁的各种计算方式对比Table 1　Comparison of various computing methods

图9　悬臂梁上表面σx应力Fig.9　Curves of σx of the upper surface ofcantilever beam

采用完全多项式的实体分析，其意义在于整体应力的准确性。如表2所示，当采用4阶完全多项式时，悬臂梁上表面的σy应力与施加的分布荷载符合很好(x<4 m区域在加密网格后也会如此)，另外，上表面的τxy以及下表面的τxy和σy均接近于0。而引入假设后，上述应力是不受控制的。

表2　悬臂梁上表面σy应力(采用4阶完全多项式)Table 2　Values ofσy of the upper surface of cantileverbeam (using 4-order polynomials)

注：括号内的数值为理论值

6.2　直梁的自由端受剪力作用

如图10(a)所示，直梁的几何尺寸、材料参数和约束情况同前例，在梁的自由端作用10 kN的剪力荷载。为验证局部坐标系下的公式和程序的正确性，分别考虑梁沿着水平向、垂直向和45°的3个方向。

本算例采用Timoshenko梁的计算方式及一维积分公式，并在固定端布置一个窄条以准确施加边界条件。采用3阶多项式，3个方向计算得到的自由端的挠度均为0.134 m，与材料力学解的0.133 m很接近。梁的上表面水平向应力几乎与材料力学解完全一致，各截面的平均剪应力均为10 kN/m2。

如图10(b)所示，再考虑变截面梁，固定端处的梁高为2 m，自由端处为1 m，其间为线性变化。自由端的挠度为0.027 7 m，与实体分析的计算结果一致。固定端顶部的水平向应力为149.28 kN/m2，与材料力学解的150.00 kN/m2很接近。

图10　悬臂梁的自由端受剪力作用Fig.10　 A cantilever beam subjected toa shear load at the free end

图11　折梁底部受剪力作用Fig.11　A folded beamsubjected to a shearload at the bottom

6.3　折　梁

如图11所示，各为10 m长的2段直梁折转90°相连，均划分为1个独立覆盖，梁的截面高度仅为0.1 m。弹性模量E=3×108kN/m2，泊松比为0。左端固定，底部施加2.5 kN的剪力荷载。

本算例采用Timoshenko梁的计算方式及一维积分公式(转折处条形区域仍采用实体积分)，并在左侧的固定端布置一个窄条以准确施加边界条件。

采用3阶多项式，计算得到荷载施加点的水平向位移为-0.133 m，垂直向位移为-0.05 m，与材料力学的结果一致。固定端顶部的水平向应力为14 980 kN/m2，与材料力学解的15 000 kN/m2很接近。

本例中值得关注的是，独立覆盖的长度与高度之比达到100∶1，但未出现有限元法的Timoshenko梁单元在求解细长梁时的剪切自锁现象。另外采用完全多项式进行实体分析，得到几乎一样的结果，也未出现影响计算精度的数值病态。

7　结　语

本文提出梁的独立覆盖分析方法，其思路可以直接推广到三维的梁板壳分析，特别是板壳，适用于Kirchhoff理论、Reissner-Mindlin理论，甚至是完全的实体分析。在积分方式上可以先沿厚度、然后在中面积分，当然，转折处的实体积分是否可以简化还有待研究。

本文不限于讨论梁的分析方法，而是希望找到一条解决梁板壳类问题的新途径。实际上，梁的分析相对简单，目前的有限元法已能很好地应对，然而板壳分析仍需改进。相对于有限元法而言，本文方法的特点是：

(1)与实体分析采用同一模式(包括基于实体的平衡微分方程等控制方程)，仅需在独立覆盖函数的选择上采用完全多项式或使其中的某些项不参与分析，就可以分别实现实体分析。仅要求近似场函数的C0连续性，比Euler-Bernoulli梁和薄板壳的Kirchhoff理论所要求的C1连续性要简单得多。这种方式还便于与实体单元的连接，即：不管是实体还是梁板壳，都可以在各自的独立覆盖中根据所在区域的特点定义覆盖函数(完全多项式或者引入某些假设)，只需通过覆盖重叠区域内的线性变化的单位分解函数连成整体。这是独立覆盖流形法的基本路径，方法单一却十分有效。

(2)对于Timoshenko梁理论和厚板壳的Reissner-Mindlin理论，本文方法在覆盖函数的选取上具有挠度比转角高1阶的内在特性，从而避免了有限元法在求解细长梁或薄板壳时的剪切自锁。同时，只要覆盖函数阶次>1，就具备了描述纯弯曲的能力。建议采用这种挠度和转角独立定义的方式，厚或薄的梁板壳均适用。

(3)通常应用的多项式阶次不会太高，这种情况下，本文方法(即使是完全的实体分析)不存在由于厚度远小于其他尺度而导致的数值病态。

本文方法之所以能避免梁板壳有限元存在的问题，是因为在独立覆盖中直接给定能准确模拟梁板壳变形的近似函数，而有限元法用单位分解函数(即有限元法基于插值方式的形函数)来构造近似函数，所受的限制太多，比如结点个数与多项式阶次的匹配、网格形状与网格连接的影响等等。本文方法同样引入梁板壳的基本假设而减小计算规模，并提供了从低阶到高阶函数的多种选择，因此与有限元法相比计算代价不会太高。高阶相对于低阶的优势是逼近快，虽然公式推导相比常规有限元的常数变量稍显复杂，但此过程是一劳永逸的。

致谢:感谢石根华博士的指导！

参考文献：

[1]ZIENKIEWICZ O C, TAYLOR R L.有限元方法[M].5版.庄茁，岑松,译.北京: 清华大学出版社, 2006.

[2]王勖成．有限单元法[M]．北京：清华大学出版社，2003.

[3]SHI G H. Manifold Method of Material Analysis[C]∥U.S. Army Research Office. Transactions of the Ninth Army Conference on Applied Mathematics and Computing. Minneapolis Minnesota, U. S. A. June 18-21, 1991:51-76.

[4]BABUSKA I, MELENK J M. The Partition of Unity Method[J]. International Journal for Numerical Methods in Engineering, 1997, 40(4):727-758.

[5]ZHENG H, LIU Z J, GE X R. Numerical Manifold Space of Hermitian Form and Application to Kirchhoff’s Thin Plate Problems[J]. International Journal for Numerical Methods in Engineering, 2013, 95(9): 721-739.

[6]祁勇峰, 苏海东, 崔建华．部分重叠覆盖的数值流形方法初步研究[J].长江科学院院报, 2013,30(1):65-70.

[7]SU Hai-dong, QI Yong-feng, GONG Ya-qi,etal. Preliminary Research of Numerical Manifold Method Based on Partly Overlapping Rectangular Covers[C]∥DDA Commission of International Society for Rock Mechanics. Proceedings of the 11th International Conference on Analysis of Discontinuous Deformation (ICADD11). Fukuoka, Japan, August 27-29, 2013, London :Taylor & Francis Group, 2013: 341-347.

[8]苏海东, 祁勇峰, 龚亚琦,等. 任意形状覆盖的数值流形方法初步研究[J]. 长江科学院院报, 2013, 30(12): 91-96.

[9]苏海东，颉志强，龚亚琦, 等．基于独立覆盖的流形法收敛性及覆盖网格特性[J]. 长江科学院院报，2016,33(2)：131-136.

[10] 苏海东，颉志强．独立覆盖流形法的本质边界条件施加方法[J]. 长江科学院院报，2017，34(12)：140-146.

[11] 苏海东,祁勇峰,龚亚琦．裂纹尖端解析解与周边数值解联合求解应力强度因子[J]．长江科学院院报, 2013，30(6)：83-89.

[12] 申向东．材料力学[M]．北京：中国水利水电出版社，2012.

[13] 林绍忠. 用预处理共轭梯度法求解有限元方程组及程序设计[J]. 河海大学学报, 1998, 26(3): 112-115.