小净距隧道群稳定性判定因素及施工顺序优化研究

2018-04-17，，，，

长江科学院院报 2018年4期

，，　，，

(1.山东科技大学土木工程与建筑学院，山东青岛　266590；2.中铁隧道勘测设计院有限公司，天津　300133)

1　研究背景

岛式地铁车站进站口处需开挖多个隧洞，以满足列车及人员进站要求。由于功能限定，隧道净距较小，且隧道群净高较大，时常需要穿越不同性质地层，导致隧道群开挖时会产生显著的时空效应及群洞效应，对隧道群施工时的整体稳定产生重要影响。因此，探究隧道群稳定性主要判定指标并明确合理的开挖顺序，对于提高隧道群的整体稳定具有重要意义。

由于隧道群整体稳定为一个综合性指标，某些判定因素在现场测试中难以测量，且对多个判定指标进行分析时，指标之间多以无干扰、相互独立的方式分析为主[1-3]，很难分析各判定指标间的关联性以及某一判定指标对隧道群稳定性的影响程度。灰色关联理论与有限差分法相结合[4-5]，为隧道群稳定性判定指标的主次关系及隧道群施工方案最优化提供了新的研究思路。考虑到隧道群施工稳定性可由最大拱顶沉降、塑性区体积、夹岩最大剪应力、锚杆最大轴力等判定指标来评价[6-8]，且各指标之间可能存在不确定、模糊的耦合作用，特选用对样本容量要求较低的模糊灰色关联度模型进行分析[9-10]。如今，较多学者利用灰色关联分析法对隧道及稳定性影响因素进行了分析[11-14]，但对稳定性判定因素之间的主次关系所做的研究甚少； Wu等[15]、王渭明等[16]分别利用灰色关联分析法对公路建设、巷道挖掘进行了施工顺序的优化选择，但是利用该方法对隧道群施工方案优化研究方面少有先例。

基于上述原因，本文选取工程典型性施工方案，采用有限差分软件对隧道群进行数值模拟，结合模糊灰色关联模型，分析模拟隧道群稳定性判定指标的关联程度，建立相关判定指标对隧道稳定性反映程度的评价方法，可理清各判定指标对隧道群稳定性反馈度的主次顺序，并为隧道群施工顺序提供最优解。

2　隧道群模型建立及结果分析

2.1　模型构建及开挖方案选取

青岛地铁3号线敦化路站位于南京路与敦化路交叉路口南侧，为地下一层分离岛式车站，车站线位为南北向，沿南京路敷设。车站所处地段北高南低，地面高差较大，主体埋深处于地下15～21 m之间。

本文所选分析区域位于敦化路车站南侧，且处于南端站厅以北位置，其整体平面布置如图1所示。研究区域共包含4条线路隧道，其中，左、右线隧道为结构主体，台阶法施工，断面尺寸为9.5 m×10.15 m；中线隧道采用全断面开挖工法，断面尺寸为3 m×4 m；上线隧道为南侧下行通道，CRD法施工，宽11 m，高6.1 m，与中线隧道相距5.35 m，与主体结构最小净距4.2 m，断面如图1所示。该地地质以上软下硬为特性的土岩复合地层为主，隧道群上覆全风化、下卧微风化花岗岩层，共穿越3种不同岩性地层。考虑因隧道施工引起地层沉降突变，采用小导管、注浆锚杆对相关部位进行超前加固。因研究区域尺寸较大，为避免隧道开挖引起端部效应放大，故左、右、下侧距离取至距隧道外边缘2.5倍隧道净宽，且受垂直于相应侧面的铰接约束。以该实际工程为背景，建立如图2所示的隧道群分析模型。

图1　隧道群断面示意图Fig.1　Schematic diagram of tunnel group section

图2　隧道群三维计算模型Fig.2　Three-dimensional models of tunnel group

由于各隧道之间净距很小，故考虑采取相应工程措施对夹岩部位及左、中、右3线隧道拱顶位置进行加固。数值计算过程中，注浆加固及小导管超前支护采用提高加固区围岩参数进行模拟，初期支护、二次衬砌采用实体弹性单元模型，锚杆选用cable单元，钢支撑选用beam单元。隧道群围岩参数取值参照工程勘测资料，选用参数如表1所示。

多孔隧道群洞效应的存在，使隧道群某条线路隧道施工对相邻隧道围岩应力、变形及隧道群整体稳定产生重要影响。探究隧道群洞合理开挖顺序，可保证隧道群施工中具有可靠的整体稳定性能。结合工程现场实际情况，确定4线隧道6种典型隧道施工模拟方案，如表2所示。

表1　围岩物理力学参数Table 1　Physical and mechanical parameters ofsurrounding rock

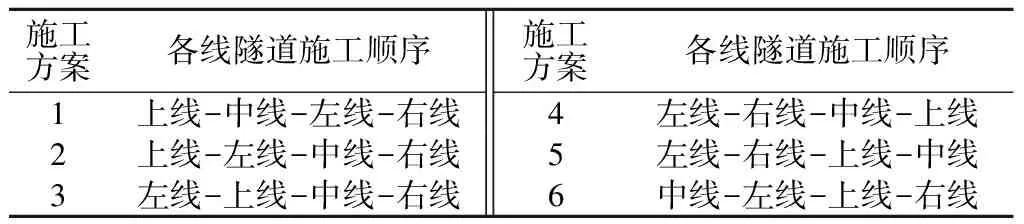
表2　隧道群施工方案及对应施工顺序Table 2　Schemes and sequences of tunnelgroup construction

2.2　破坏准则确定及模拟结果分析

Von Mises模型可被描述为岩体受中主应力影响的弹塑性屈服模型，其应力偏张量第二不变量固定为某一定值时，该点即进入塑性状态。由于该模型塑性势函数与屈服函数相同，因而具有明显的相关流动性[17]。对此，采用与Mohr-Coulomb相匹配的修正Drucker-Prager模型，该模型不仅将静水压力引入Von Mises屈服准则，且其采用非关联流动法则，屈服面与塑性势面唯一对应[18]，因而能较好地适应于存在静水压力的岩体工程。当应力空间为三维状态时，Drucker-Prager破坏准则可定义为

(1)

式中：I1为应力张量第一不变量；J2为应力偏量第二不变量；aφ及k为材料相关参数。

aφ和k均为应力罗德角θσ的相关函数，即：

(2)

(3)

其中,

(4)

式中：a为常系数；σ1，σ2，σ3为主应力值；c，φ分别为岩土材料的黏聚力及内摩擦角，该数据可由工程地质勘察资料查得。

由式(4)可知，应力罗德角反映空间一点的受力状态形式。θσ取不同值，材料在该点的受力状态不同。对于发生纯剪破坏的材料，σ1= -σ3=τ，σ2=0，因而θσ=0°，将其代入式(3)及式(4)，可得：

aφ=(sinφ)/3,

(5)

k=ccosφ。

(6)

基于受扰动围岩弹塑性及非正交流动性性质，当进行隧道群施工性态分析时，选用修正的Drucker-Prager模型，并结合青岛敦化路站南侧区域工程实际情况，采用FLAC3D数值模拟对6套典型施工方案进行比较，以深入揭示不同施工顺序下隧道围岩变形、结构受力、塑性区分布等稳定性演化规律，由此得到不同施工顺序下其模拟结果判定指标取值(如表3所示)，各方案判定指标的变化情况图3所示。

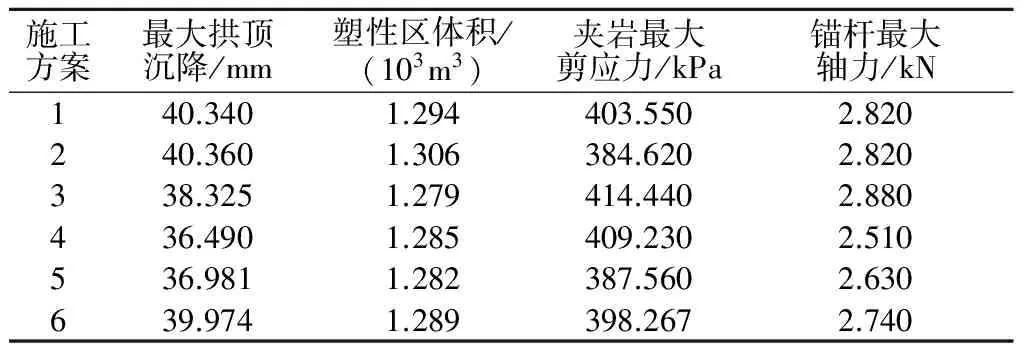
表3　基于数值模拟的各方案判定指标取值Table 3　Values of determinant indexes in differentsimulation schemes

图3　各施工方案判定指标变化曲线Fig.3　Curves of determinant indexes variation indifferent simulation schemes

隧道群稳定性判定指标数值越小，所得效果越好。由图3知：执行方案4时，隧道最大拱顶沉降与锚杆最大轴力为6个方案的最小值，但围岩塑性体积及夹岩最大剪应力最小值分别产生于方案3及方案2中。因而对隧道群施工方案的选取不能根据模拟数据进行直观判定，且4种隧道稳定性判定指标之间关联度、各判定指标对隧道群稳定性的重要程度也难以根据上述图表进行直观反映，故采用模糊灰色关联分析法对所得模拟值进行处理，以期解决上述问题。

3　隧道群施工稳定性判定因素模糊灰色关联分析模型

3.1　灰色关联分析模型

灰色关联分析模型可用于对隧道群稳定性判定指标的作用程度进行量化分析，可由灰色关联度表示参考序列与比较序列之间的关系，关联度数值越高，表明该关联度相对应的比较序列对参考序列影响程度越重要。

参考序列及比较序列的选取为关联分析过程的首要任务。将不同施工顺序下影响隧道群稳定性的某个因素取值进行统计，并使其作为参考序列，其每组数据均可反映隧道群稳定性在某一确定表现因素下的发展变化趋势，其表现形式为

Yi=yikk=1,2,…,m。

(7)

式中：Yi为隧道群稳定性影响因素分析模型中的参考序列矩阵；yi(k)为该参考序列中第k个组成元素；m为该参考序列组成元素的个数。

比较序列为影响隧道群施工稳定性判定因素所组成的数据序列。对于改变施工顺序而引起的隧道群整体稳定性判定因素关联分析中，其施工顺序假设为m种，而被研究隧道群稳定性判定因素有n+1个(当进行施工方案优选分析时，施工顺序假设为n种，稳定性判定因素为m+1个)，则灰色关联分析模型中的参考序列矩阵Yi所对应的比较序列Zi为

Zi=zikk=1,2,…,m,i=1,2,…，n。

(8)

对于所选的研究因素，其物理含义及量纲各异。为提高灰色关联分析的精度，保证分析后所得结果质量，需对有关隧道群稳定性的不同量纲的特征参数进行无量纲化处理。对于不同的研究对象，选用不同的无量纲处理方法。对隧道群稳定性判定因素进行关联分析时，原始数据选用min-max阈值法进行无量纲处理，其转换矩阵Yt(k)与Zj(k)中的元素可表示为：

(9)

(10)

式中：maxzi(k)，minzi(k)分别为zi(k)的最大值和最小值；maxyi(k)，minyi(k)分别为yi(k)的最大值和最小值。

对隧道开挖方案优选分析时，由于所选隧道群稳定性判定指标为“越小越好”的成本型参数，故以每个分析指标的最小值作为参考序列进行分析，比较序列无量纲转换形式可表示为

(11)

灰色关联度模型中无量纲转换后比较序列对参考序列的关联系数ξtj(k)可表示为

(12)

隧道群稳定性判定因素灰色关联模型中的分辨系数θ可由以下方法确定:

(13)

当0≤ΘΔ≤1/3时，θ的范围为

ΘΔ≤θ≤1.5ΘΔ。

(14)

当ΘΔ>1/3时，θ的范围为

1.5ΘΔ≤θ≤2ΘΔ。

(15)

ΘΔ满足式(14)时，表示关于隧道群稳定性判定因素的关联分析模型中的参考序列或对比序列取值出现异常；ΘΔ满足式(15)时，说明灰色关联模型中的参考序列或对比序列数据正常。

3.2　模糊灰色关联度模型

为提升隧道群稳定性判定因素灰色关联分析模型的测评精准率，采用Euclid距离对参考序列及比较序列的差异程度进行有效表示[19]。结合隧道群施工顺序及稳定性判定因素实际选取情况，参考序列或比较序列的权重可表示为

ωjk=ω1k,ω2k,…,ωmkk=1,2,…,n。(16)

则关联模型中的Euclid灰色关联度r′tj可表示为

(17)

由于参考序列及比较序列之间存在较大概率的线性比例关系，为降低因此导致的计算结果误差，采用夹角余弦法所得的模糊隶属系数rtj与灰色关联系数r′tj相结合的方法，得到关于隧道群稳定性判定因素的模糊灰色关联度Rtj，即

(18)

式中：rtj表示参考序列与比较序列之间的相似度，由两者夹角余弦值进行确定。

4　结果分析

4.1　隧道群稳定性判定因素关联程度分析

4.1.1最大拱顶沉降作为参考序列

结合表3所述各施工方案稳定性判定指标取值(下同)，当最大拱顶沉降s作为参考序列Y时，则可由塑性区体积v、夹岩最大剪应力τ、锚杆最大轴力f组成比较序列向量矩阵Z。Y和Z各自表现形式为：

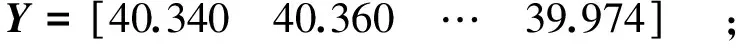
(19)

(20)

将式(19)和式(20)根据式(9)和式(10)进行无量纲处理后可得系数矩阵为

(21)

根据式(13)—式(15)计算可得绝对差均值与最大绝对差的比值ΘΔ=0.344>1/3，故分辨系数θ修正后的取值区间为0.516≤θ≤0.688，此处取θ=1.75ΘΔ=0.601，将θ代入式(12)后计算得各判定因素灰色关联系数矩阵为

(22)

考虑工程实际，各判定因素对隧道群稳定性表现特征不存在本质区别，即本文取相同权重ωjk=1/18。由式(17)及式(18)可得当参考序列为最大拱顶沉降s时比较序列Euclid灰色关联度r′1、模糊隶属度余弦值r1、模糊灰色关联度R1的计算结果，如表4所示。

表4　参考序列为最大拱顶沉降时的3种关联度分析结果Table 4　Results of correlation analysis with maximumvault settlement as reference series

由表4可知：当塑性区体积v、夹岩最大剪应力τ、锚杆最大轴力f对隧道最大拱顶沉降s的模糊灰色关联度R1=[R1vR1τR1f]=[0.755 0.593 0.784]，由此可知R1f>R1v>R1τ。因此，隧道最大拱顶沉降与锚杆最大轴力之间的模糊灰色关联度较高，说明锚杆最大轴力对隧道最大拱顶沉降有较大影响。

4.1.2塑性区体积作为参考序列

当塑性区体积v作为参考序列Y时，则可由隧道拱顶最大沉降s、夹岩最大剪应力τ、锚杆最大轴力f组成比较序列向量矩阵Z。Y和Z各自表现形式为：

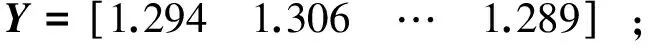
(23)

(24)

将式(23)和式(24)根据式(9)和式(10)进行无量纲处理后可得系数矩阵为

(25)

根据式(13)—式(15)计算可得绝对差均值与最大绝对差的比值ΘΔ=0.366>1/3，故分辨系数θ修正后的取值区间为0.549≤θ≤0.732，此处取θ=1.75ΘΔ=0.641，将θ代入式(12)后计算得各判定因素灰色关联系数矩阵为

(26)

与表4类似，可得当参考序列为塑性区体积v时比较序列Euclid灰色关联度r′2、模糊隶属度余弦值r2、模糊灰色关联度R2的计算结果，如表5所示。

表5参考序列为塑性区体积时的3种关联度分析结果
Table5Resultsofcorrelationanalysiswithplasticzonevolumeasreferenceseries

判定指标r′2r2R2s0．6340．8870．761τ0．6880．3850．536f0．8550．7510．803

由表5可知：隧道拱顶最大沉降s、夹岩最大剪应力τ、锚杆最大轴力f对塑性区体积v的模糊灰色关联度R2=[R2sR2τR2f]=[0.761 0.536 0.803]，由此可知R2f>R2s>R2τ。因此，隧道塑性区体积与锚杆最大轴力之间的模糊灰色关联度较大，说明锚杆最大轴力对隧道塑性区体积有较大影响。

4.1.3夹岩最大剪应力作为参考序列

当夹岩最大剪应力τ作为参考序列Y时，则可由最大拱顶沉降s、塑性区体积v、锚杆最大轴力f组成比较序列向量矩阵Z。Y和Z各自表现形式为：

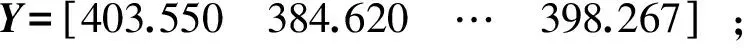
(27)

(28)

将式(27)和式(28)根据式(9)和式(10)进行无量纲处理后可得系数矩阵为

(29)

根据式(13)—式(15)计算可得绝对差均值与最大绝对差的比值ΘΔ=0.457>1/3，故分辨系数θ修正后的取值区间为0.686≤θ≤0.914，此处取θ=1.75ΘΔ=0.800，将此代入式(12)后计算得各判定因素灰色关联系数矩阵为

(30)

与表4类似，可得当参考序列为夹岩最大剪应力τ时比较序列Euclid灰色关联度r′3、模糊隶属度余弦值r3、模糊灰色关联度R3的计算结果，如表6所示。

表6　参考序列为夹岩最大剪应力时的3种关联度分析结果Table 6　Results of correlation analysis with maximumshear stress as reference series

由表6可知：隧道拱顶最大沉降s、塑性区体积v、锚杆最大轴力f对夹岩最大剪应力τ的模糊灰色关联度R3=[R3sR3vR3f]=[0.620 0.552 0.709]，由此可知R3f>R3s>R3v。因此，夹岩最大剪应力与锚杆最大轴力之间的模糊灰色关联度较大，说明锚杆最大轴力对夹岩最大剪应力有较大影响。

4.1.4锚杆最大轴力作为参考序列

当锚杆最大轴力f作为参考序列Y时，则可由最大拱顶沉降s、塑性区体积v、夹岩最大剪应力τ组成比较序列向量矩阵Z。Y和Z各自表现形式为：

(31)

(32)

将式(31)和式(32)根据式(9)和式(10)进行无量纲处理后可得系数矩阵为

(33)

根据式(13)—式(15)计算可得绝对差均值与最大绝对差的比值ΘΔ=0.317<1/3，故分辨系数θ修正后的取值区间为0.317≤θ≤0.476，此处取θ=1.25ΘΔ=0.396，将此代入式(12)后计算得各判定因素灰色关联系数矩阵为

(34)

与表4类似，可得当参考序列为锚杆最大轴力f时比较序列Euclid灰色关联度r′4、模糊隶属度余弦值r4、模糊灰色关联度R4的计算结果，如表7所示。

表7参考序列为锚杆最大轴力时的3种关联度分析结果
Table7Resultsofcorrelationanalysiswithmaximumaxialforceofboltasreferenceseries

判定指标r′4r4R4s0．5600．9250．743v0．8170．7510．784τ0．5760．7160．646

由表7可知：隧道拱顶最大沉降s、塑性区体积v、夹岩最大剪应力τ对锚杆最大轴力f的模糊灰色关联度R4=[R4sR4vR4τ]=[0.743 0.784 0.646]，由此可知R4v>R4s>R4τ。因此，锚杆最大轴力与塑性区体积之间的模糊灰色关联度较大，说明塑性区体积对锚杆最大轴力有较大影响。

4.1.5结果讨论

根据以上分析，当各判定指标分别为参考序列时，计算所得隧道群稳定性判定因素的模糊灰色关联结果如表8所示。

表8　模糊灰色关联分析结果汇总Table 8　Summary of fuzzy grey relational analysis

注：∑表示某一列判定因素关联度相加值，为该因素对隧道群稳定性的综合反映

根据表8可知,各判定因素综合测评值∑=[∑s∑v∑τ∑f]=[3.124 3.091 2.775 3.296]，显然∑f>∑s>∑v>∑τ。由此表明锚杆最大轴力是4个指标中最主要的判定因素，该指标在隧道群稳定性判定因素中起主导作用，其次为最大拱顶沉降和塑性区体积，夹岩最大剪应力在隧道群稳定性判定因素中所起作用影响甚微。并且，当以其余3个隧道群稳定性判定指标作为参考序列时，最大锚杆轴力与各参考序列的关联度均为最大值，说明锚杆最大轴力对隧道群稳定性判定指标均有重要影响。因而，在隧道群施工中，应着重动态监测夹岩处锚杆，采取相关措施降低最大轴力值，确保隧道群施工的安全稳定。

4.2　隧道群施工开挖顺序方案优选

4.2.1灰色关联度分析

最大拱顶沉降s、塑性区体积v、夹岩最大剪应力τ以及锚杆最大轴力f等判定指标均为“越小越好”的成本型参数，故相对最优方案的参数指标(参考序列)为

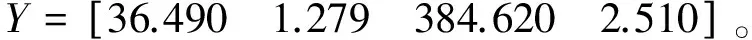
(35)

最大拱顶沉降s、塑性区体积v、夹岩最大剪应力τ、锚杆最大轴力f所组成的矩阵为比较序列Z，则

(36)

据式(9)和式(11)对式(35)和式(36)进行无量纲处理后可得系数矩阵为

根据式(13)—式(15)计算可得绝对差均值与最大绝对差的比值ΘΔ=0.352>1/3，故分辨系数θ修正后的取值区间为0.528≤θ≤0.704，此处取θ=1.75ΘΔ=0.616，将θ代入式(12)后计算得各判定因素灰色关联系数矩阵为

(38)

考虑工程实际，各判定因素对隧道群稳定性表现特征不存在本质区别，即本文取相同权重ωjk=1/24。由式(17)及式(18)可得当参考序列为成本型参数时各施工方案的Euclid灰色关联度r′5、模糊隶属度余弦值r5、模糊灰色关联度R5的计算结果，如表9所示。

表9　各施工方案顺序有关的灰色关联分析Table 9　Grey relational analysis for differentconstruction schemes

图4　不同施工方案下Von Mises等效应力云图Fig.4　Nephogram of Von Mises equivalent stress in different construction schemes

表9表明：各施工方案相关参数对相对于成本型参数的模糊灰色关联度R5=[R51R52R53R54R55R56]=[0.828 0.819 0.815 0.909 0.875 0.822]，显然有R54>R55>R51>R56>R52>R53，且R54与R55数值相差较小。模糊灰色关联度越大，表明评价方案与理想方案的接近程度越高，因此方案4与方案5为隧道施工顺序的优选方案。

4.2.2等效应力方法验证

Von Mises应力是基于剪切应变能的一种等效应力，是对单元体的形状改变能达到一定程度时材料开始产生屈服的体现，该等效应力为正应力与剪切应力分量的组合，使我们可以快速确定模型中最危险区域。6种不同开挖方案下的Von Mises等效应力云图如图4所示。

等效应力越大，围岩越易进入塑性状态。由Von Mises应力云图可知，6种开挖方案下等效应力集中区域均位于隧道断面周边区域，且最大等效应力位于左线及右线隧道拱脚位置处，说明该位置易产生塑性屈服，左线隧道与上线隧道中间夹岩、右线隧道与上线隧道中间夹岩位置处具有较大的等效应力，说明该位置围岩需采取措施进行加固以防止隧道因产生塑性屈服导致的失稳破坏。同时对比6个施工方案等效应力云图可知，方案4及方案5上线隧道与中线隧道中间夹岩以及中线隧道底板下方低应力区范围较大，说明此位置围岩不易产生塑性破坏；方案4与方案5的最大等效应力值低于其他施工方案的最大等效应力值，说明采用方案4或方案5施工可保证隧道群具有较好的安全稳定性。结合模糊灰色关联度分析所得结论，方案4与方案5为隧道群施工的优选方案。

5　结　论

(1)运用FLAC3D软件对地铁车站4线隧道群洞6种典型开挖方案进行数值模拟，结合模糊灰色关联分析理论，将模拟所得隧道群稳定性4因素进行关联度分析，得出4种判定因素对隧道群稳定性的影响程度及隧道群施工最优方案。

(2) 锚杆最大轴力是判定隧道群稳定性的最主要因素，其次为最大拱顶沉降和塑性区体积，夹岩最大剪应力是隧道群稳定性判定的次要因素。

(3) 依靠模糊灰色关联分析理论，方案4与方案5中各影响参数与成本型参数的关联度较大，说明“左线-右线-中线-上线”及“左线-右线-上线-中线”的隧道开挖顺序为优选方案，对比分析各施工方案的Von Mises等效应力验证该施工方案的准确性。

参考文献：

[1]郑颖人，邱陈瑜，张红，等. 关于土体隧洞围岩稳定性分析方法的探索[J]. 岩石力学与工程学报，2008，27(10): 1968-1980.

[2]张志强，何本国，关宝树. 节理岩体隧道围岩稳定性判定指标合理性研究[J]. 现代隧道技术，2012，49(1): 12-19.

[3]杨臻，郑颖人，张红，等. 岩质隧洞围岩稳定性分析与强度参数的探讨[J]. 地下空间与工程学报，2009，5(2): 283-290.

[4]PENG G H， DENG X G， YU L. Optimization Layout of Slope Displacement Monitoring Points Based on Numerical Computation[J]. Electronic Journal of Geotechnical Engineering，2012，17: 2851-2860.

[5]付建军，邱山鸣，赵海斌，等. 基于灰色关联度的边坡稳定影响因素分析[J]. 长江科学院院报，2011，28(1): 53-57.

[6]李利平，李术才，张庆松，等. 小间距隧道施工性态监测与稳定性分析[J]. 岩土力学，2006，27(增1): 333-338.

[7]仇文革，孔超，刘凯. 城市复杂隧道群中超小净距夹岩稳定性研究[J]. 中国铁道科学，2014，35(6): 41-47.

[8]陈秋南，赵磊军，谢小鱼，等. 浅埋偏压大跨花岗岩残积土小净距隧道合理间距研究[J]. 中南大学学报 (自然科学版)，2015，46(9): 3475-3480.

[9]ZHANG X，JIN F，LIU P D. A Grey Relational Projection Method for Multi-attribute Decision Making Based on Intuitionistic Trapezoidal Fuzzy Number[J]. Applied Mathematical Modelling，2013，37(5): 3467-3477.

[10] 陈强，周先雁. 岩锚梁稳定性影响因素模糊灰色关联分析模型及其应用[J]. 中南大学学报 (自然科学版)，2015，46(9): 3488-3495.

[11] 靳晓光，李晓红，高芃，等. 隧道围岩位移的灰色优化模型预测[J]. 重庆大学学报(自然科学版)，2002，25(1): 1-5.

[12] 何伟. 灰色系统理论在隧洞工程中的应用研究[D]. 西安: 西安理工大学，2010.

[13] 李炎延，郑颖人，康楠. 隧洞稳定性影响因素的敏感性分析[J]. 地下空间与工程学报，2015，11(2): 491-498.

[14] 谭鹏，曹平. 基于灰色关联支持向量机的地表沉降预测[J]. 中南大学学报(自然科学版)，2012，43(2): 632-637.

[15] WU C H，HSIEH T Y，CHENG W L，etal. Grey Relation Analysis of Causes for Change Orders in Highway Construction[J]. Construction Management and Economics，2004，22(5): 509-520.

[16] 王渭明，吕显州，秦文露. 半煤岩巷道快速综掘截割顺序优化研究[J]. 采矿与安全工程学报，2015，32(5): 771-777.

[17] 郑颖人，沈珠江，龚晓南. 广义塑性力学——岩土塑性力学原理[M]. 北京：中国建筑工业出版社，2002.

[18] 赵尚毅，郑颖人，刘明维，等. 基于 Drucker-Prager 准则的边坡安全系数定义及其转换[J]. 岩土力学与工程学报，2006，25(1): 2730-2734.

[19] 乔景顺. 变权欧氏距离模型在边坡稳定性评价中的应用[J]. 长江科学院院报，2013，30(7): 81-85.