不同流量下渐扩段局部水头损失数值模拟

　

(陕西铁路工程职业技术学院，陕西 渭南　714000)

1　研究背景

天然河道的基本平面形态有顺直型、弯曲、蜿蜒摆动、分叉等，河道流路渐缩或渐扩现象很普遍，在渐缩或渐扩过程中会产生局部水头损失。在实际工程中，局部水头损失的计算对水利工程的设计有重要的指导意义。在吴持恭[1]水力学课本中对于局部水头损失有相关研究，其是在模型试验的基础上，根据连续性方程、动量方程结合在2个渐变流断面上忽略沿程水头损失建立的能量方程得到1个经验的局部水头损失公式。

目前对局部水头损失的研究大多集中在利用模型试验得出，或者是对文献[1]公式进行进一步的简化以此得出较为接近实际的局部水头损失公式。赵宝峰等[2]结合实验考虑了两段面间的沿程水头损失，对hj进行推导计算，对公式重新修正；张沁[3]采用RNGκ-ε紊流模型对Re>4 400时的圆管中突然扩大和突然缩小的局部水头损失进行数值模拟；李栋浩等[4]通过对一定水头时不同突缩比塑料圆管的局部水头损失试验，分析了局部阻力系数与流速、管径及温度之间的关系；吴永妍等[5]通过物理模型试验研究了从梯形明渠到马蹄形隧洞进口过渡段的水面衔接特点和局部水头损失规律；李梅华等[6]在考虑局部阻碍的情况下得出明渠恒定非均匀流的水面线变化曲线规律；闫旭峰等[7]运用声学多普勒流速仪测量了渐变河道模型的水流结构；谢海英[8]利用Spalart-Allmaras湍流模型，对雷诺数Re<5 500时管路中突然扩大的局部水头损失进行了数值模拟。上述文献大多研究的是突扩或突缩断面的水头损失，对于渐扩或渐缩断面研究甚少，研究时更多的是利用手算减小计算的步长，以使两断面近似为缓流断面从而利用能量方程进行计算。这种计算方法在实际应用中要求精度不高的情况下是可行的，但比较麻烦。本文针对这种方法提出利用MIKE软件模拟的电算办法，并利用实例进行验证，证明MIKE软件计算的合理性和实用性。

图1　河道断面计算简图Fig.1　Sketch of channelsection

图2　渐扩段计算简图Fig.2　Sketch of graduallybroadened channel

2　模型建立

本文计算实例由明渠段、渐扩段、明渠段组成，上游9.6 m×3 m矩形明渠，长99.7 m，下游16.2 m×4 m矩形明渠，长71.8 m，中间渐扩段长10 m，计算简图如图1。

其中2-2断面至3-3断面间为渐变段，由于从上游矩形明渠过渡到下游矩形明渠过程中，不仅会产生沿程水头损失，还会受到局部水头损失的影响，因此较为准确计算渐变段水面线变化规律，需将此10 m长断面划分为一段段的河段，且划分越细,最终水面线计算结果越精确，本文在渐变段中选取20个断面，断面划分情况见图2。其中，每2个断面间仍有4个断面。

3　模拟工况及数值模拟条件

本文采用DHI MIKE21软件的水动力(HD)模块进行模拟，水动力模型的控制方程有：

质量守恒方程

(1)

x方向动量方程

(2)

y方向动量方程

(3)

式中：ζ为表面水位(m)；t为时间(s)；p，q为沿x和y方向的通量密度(m3/ms)；d为水位随时间的变化量(m)；h是水深(m)；C为谢才系数(m1/2)；ρw为水密度(kg/m3)；τxx，τxy为有效切应力分量(N/m2)；f为风摩擦系数，无量纲；V，Vx分别为风速及其在分方向速度(m/s)；Ω为科氏系数(s-1);pa为大气压(N/m2)。

本文是在清水定床工况下模拟30，45，60，75，90 m3/s 5种不同流量情况下渐扩段局部水头损失的变化规律。河道底坡为0.52%，糙率0.017，上游入口条件为流量，即取上游恒定水流条件，下游出口条件取为稳定水深水流条件，计算中固壁按定边界条件处理。采用交替格式隐式算法(Alternating Direction Implicit Method，ADI)计算，用这种交替方向隐式迭代法对动量方程、质量方程等进行迭代求解方程组。然后利用双精度扫描法(DOUBLE SWEEP)对其每个方向及单独网格线上产生的数学矩阵进行求解。计算中划分的三角网格数为1 798、网格节点数为1 041、网格平均面积为1.0 cm2。

4　计算结果与分析

4.1　流场分析

几种不同流量下渐扩段流场图，图中流速单位为m/s，如图3所示。

图3　各流量下渐扩段流速矢量分布Fig.3　Distribution of flow velocity vector in graduallybroadened channel under different discharges

根据图3可知：

(1)从上游明渠段进入渐扩段时均发生水位突降现象，且流量越大,突降越厉害，因此局部水头损失就发生在此部位。

(2)流量越大，在渐扩段流速扩散影响的范围越大，且流量越大，水流经过渐扩段后水位要经过很长一段时间才能达到平衡。

(3)不管是从上游明渠到渐扩段还是从渐扩段到下游明渠段的转折点部分流速均很大，且流速方向不规律，这是因为在从明渠到渐扩段和从渐扩段到下游明渠段过程中流速发生重分布现象，壁面流速还未适应断面的变化因此呈不规律现象分布。

4.2　水位变化

在4.1节中对5种流量下渐扩段流场分布进行了分析，本节对水位进行定量分析，并与经验值进行对比。根据文献[1]经验公式计算渐扩段沿程水面线变化趋势，与数值模拟计算值进行对比，沿渐扩段选取20个断面，对比结果见图4。

图4　水位的MIKE软件计算值与文献[1]经验公式值的对比Fig.4　Comparison of water level between MIKEsimulation and formula[1] calculation

文献[1]中经验公式计算方法为

(4)

式中hj为局部水头损失。

根据图4可得以下结论：

(1)流量越大，MIKE模拟值与经验公式计算值相差越小，这是因为随着流量的增大，断面速度分布的不均匀性逐渐减小，这与文献[8]所得结论相一致。

(2)虽然各个流量下模拟值与计算值有差别，但总体上来说二者符合较好，说明利用MIKE软件进行模拟水头损失是可行的合理的。

4.3　水头差对比

图5为渐扩段开始段与结束段水头差的MIKE软件计算值与文献[1]经验公式值的对比图。

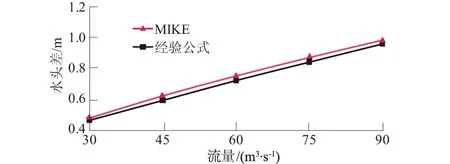
图5　水位差的MIKE软件的计算值与文献[1]经验公式值的对比Fig.5　Comparison of water head between MIKEsimulation and formula[1] calculation

根据图5可知：

(1)计算值与模拟值在渐扩段开始与结束段水头差很接近，说明MIKE模拟渐扩段水头差是合理的。

(2)流量越大，水头差越大，这个规律不管是经验值还是模拟值都是适用的，这是因为流量越大，在从上游明渠段经过渐扩段时，对渐扩段两边墙的冲击越大，水位下降越快，这与前面4.1节流场分布得出的结论相一致。

5　结　语

本文利用MIKE的水动力学模块对渐扩段水头损失进行研究，并与经验公式计算值进行对比，最终得出MIKE软件模拟水头损失是合理可靠的，且流量越大，水头损失影响越大。利用MIKE软件进行模拟不仅大大减小了计算的难度和复杂程度，而且还能够较准确地模拟出水头损失量，这与利用经验公式相比，计算方便又准确得多，经验公式计算此次10 m长断面试算水面线需要的时间远远大于模拟时间，试想若是天然河道花费的时间更是可想而知，因此本次模拟对于类似工程具有一定的实用价值。

参考文献：

[1]吴持恭.水力学上册[M].北京：高等教育出版社，2007.

[2]赵宝峰,金英子,卢玉邦,等. 对突然扩大局部水头损失的初探[J]. 东北农业大学学报,1997,28(2):71-74.

[3]张沁. 圆管突然扩大与突然缩小的局部水头损失系数的研究[J]. 科学技术与工程,2014,14(28):159-162.

[4]李栋浩,王文娥,葛茂生,等. 突然缩小圆管局部水头损失系数试验研究[J]. 水利与建筑工程学报,2011,9(4):22-24.

[5]闫旭峰,易子靖,刘同宦,等. 渐变河道水流结构及局部水头损失特性研究[J]. 长江科学院院报,2011,28(9):1-5.

[6]吴永妍,刘昭伟,陈永灿,等. 梯形明渠-马蹄形隧洞过渡段流动形态与局部水头损失研究[J]. 水力发电学报,2016,35(1):46-55.

[7]李梅华,李娴. 局部水头损失对明渠非均匀流水面曲线的影响[J]. 黄河水利职业技术学院学报,2005,17(3):10-11.

[8]谢海英. 管路突然扩大时局部水头损失的数值模拟[J]. 水资源与水工程学报,2013,24(3):152-153，160.