改进差分进化算法在物流配送中的多目标优化研究

张　新

(绍兴职业技术学院信息工程学院,浙江 绍兴 312000)

0　引言

物流配送是物流中的重要环节，它解决了物资到消费者的最后一公里问题，关系到消费者对企业的满意度和降低物流管理成本两方面。物流配送能力将直接影响物流企业的市场竟争力。为了满足用户的需要、降低物流配送成本，如何科学地规划和部署配送，已成为物流企业管理者必须考虑的问题[1]。

车辆路径问题(vehicle routing problem,VRP)最早在1959年由Dantzig提出。它是指配送中心在了解客户个性化要求的前提下(如客户物品对应单一车辆)，安排配送物品的车辆从配送中心出发，并使车辆完成所有配送服务后返回配送中心。为了解决车辆路径规划问题，1992年，J.Lawrence等人首先研究了进化算法，使带有时间窗口车辆路径问题(vehicle routing problems with time windows,VRPTW)问题得到了较好的解决。2006年，为了解决多目标VRP问题，Tan等人采用了混合多目标进化算法，较好地解决了带有时间窗口要求的VRP问题。

本文采用改进的差分进化算法，对物流配送中的车辆运输路径规划优化，提高了物流配送的经济效益，实现了物流管理的精准化和科学化[2-3]。

1　多目标物流配送及其模型

1.1　多目标物流配送问题

物流配送是物流管理中的重要环节，优化配送要素十分关键。物流配送的最大目标是让用户满意，同时要合理规划配送计划，使车辆运输成本最小化。配送过程指物资由车辆运输，从配送中心出发按时间节点要求及时送到消费者手中；然后车辆返回配送中心。这个过程涉及两个优化目标：车辆与路径。物流配送的车辆路径规划在配送过程中要满足用户物资送到时间等个性化的约束，是带有时间窗要求的多目标VRP问题。假设车辆出发点与结束点同是配送中心、所有配送车辆的最大载重质量和速度是定值、顾客的货物只能由一辆车配送并且车辆不可重复到达顾客点、顾客对配送时间有明确的要求，则路径和车辆优化目标是达到配送成本最小化[4-5]。

1.2　问题模型研究

物流配送路径优化可以采用无向连通图进行描述。假设图G=(V，E)表示无向连通图。其中，V为无向连通图中的点，代表一个顾客点或配送中心，V={vi|i=0,1,...,n}；E为两点之间的边，它代表顾客(包括配送中心)之间的距离,E={ei,j|i,j=0,1,...，n且i≠j},i、j为顾客号,n为顾客数量。本研究是带有时间窗口的VRP问题。它涉及几个约束条件：车辆载重约束、配送时间节点约束、顾客被访问次数约束等[6]。

假设配送中心需要为n个不同地点的顾客配送物资,用S表示顾客；配送中心有足够的车辆数m来满足配送需求，用K表示配送车辆,那么V={S0，S1，…，Sn},K={1,2,…，m}。差分进化算法一般采用实数方式编码，顾客点编号为1，2,…,n,并且规定配送中心为编号0[7]。T为配送所需总成本，由配送距离dij和单位车辆路程配送成本Pk计算所得。dij表示顾客之间的距离；每位顾客的货物量为gi，配送车辆的最大载重质量为Q，配送车辆是否到达顾客i处用yik表示。

带有时间窗口的物流配送多目标函数主要由两部分组成：配送成本最低和配送所用车辆最少。

式(1)和式(2)分别表示配送总费用最低和配送用车最少。

(1)

式中：T为配送总成本；dij为配送距离；Pk为车辆单位配送成本；xijk为顾客之间的车辆直达性。

(2)

式中：K为配送车辆数；x0jk为车辆从配送中心到顾客的直达性。

模型的主要约束条件如下。

式(3)表示顾客i和顾客j之间的车辆k可达性，即车辆k是否配送到顾客i处。

(3)

式中：xijk为顾客之间的车辆直达性；yjk为车辆可达性。

式(4)表示车辆可到达顾客点，且只到达一次。

(4)

式中：xijk为顾客之间的车辆直达性。

式(5)表示配送车辆载重受限，不能超重运输。

(5)

式中：gi为顾客的货物量;yik为车辆是否到达顾客点；Q为配送车辆的最大载重。

式(6)～式(8)表示车辆在不重复到达顾客点的情况下返回配送中心。

(6)

(7)

(8)

式(9)、式(10)对时间窗口进行约束控制。

sik+tij-K(1-xijk) ≤sjk

(9)

ai≤sik≤bi

(10)

式中：sik为车载k到达某一顾客处的时间要求；i=1,2,…,n;k=1,2,…,m。

2　差分进化算法

差分进化(differentialevolution,DE)算法是一种启发式优化算法。它最早在1995年，由Storn和Price首次共同提出，主要用于求解实数优化问题。该算法具有结构简单、容易实现、收敛快速和鲁棒性强的特点，目前在电磁学、模式识别、数据挖掘、人工神经网络等方面取得了较好的应用成效。

2.1　基本算法概述

DE算法的主要算法过程与其他进化算法大致相同，主要操作有变异、交叉和选择。算法起始于初始种群。初始种群随机产生。首先进行变异操作：从种群中随机选取两个不同个体进行差向量操作；随机选取不同的个体作为第三个个体，把差向量加权后按照一定的规则与第三个个体求和，其结果就是变异个体。然后进行交叉操作：按规则选定目标个体，把变异得到的变异个体与目标个体进行参数混合，产生试验个体。最后，进行选择操作，把试验个体与目标个体进行比较。如果试验个体的适应度值更优，则试验个体将取代目标个体；否则，保留目标个体。

DE算法的主要步骤为：①基本参数包括NP、F、CR；②随机产生初始化种群；③计算种群适应度值；④终止条件不满足时，进行循环，依次执行变异、交叉、选择运算，直到满足终止条件。

2.2　改进的差分进化算法

为了解决带有时间窗口的多目标物流配送优化问题，本文对基本差分算法进行了适当的改进，以下通过具体案例加以分析说明。假设配送顾客数量为8个，配送车辆的最大载重质量和行车速度统一为2 000 kg和60 km/h，顾客对配送时间有要求。

①编码与初始化种群。

首先，进行编码处理。采用自然数1～8分别表示8位顾客，并把8位顾客数字通过随机排位组合，以形成的8位数向量作为初始种群个体。这个8位向量代表车辆到达顾客处的顺序，其中的分段代表配送车辆数。如果随机产生的个体向量Xi(t)为425|681|73，则表明配送车辆为3，3辆车的配送顺序分别为：4-2-5，6-8-1，7-3。

②变异操作的改进。

变异操作的改进基本思想为：首先，选定一个随机向量Xr1(t)作为变异目标；然后，对Xr1(t)的各分矢量作乘2处理，得到新的向量Xr2(t)；最后，随机另外选取一个向量Xr3(t),将Xr2(t)-Xr3(t)，得到Vi(t+1)。分析向量Vi(t+1)各分量值：如大于限定的最大值则用其减最大值；如小于限定的最小值则用其加最大值，从中删除分向量值为0 的分向量；如出现重复分向量就留下排在前面的分向量。按序补上向量Xr1(t)中没有出现的分向量值，即可得到新的变异向量Vi(t+1)。案例说明如下。

设定：

Xr1(t)=4 2 5 6 8 1 7 3；

Xr3(t)=5 4 2 7 8 3 1 6；

Xr2(t)=2×Xr1(t)=8 4 10 12 16 2 14 6；

Vi(t+1)=Xr2(t)-Xr3(t)=3 0 8 5 8 -1 13 0。

分析Vi(t+1)，得中间结果： 3 8 5 7。

修正后变异向量Vi(t+1)=3 8 5 7 4 2 6 1。

③交叉操作。

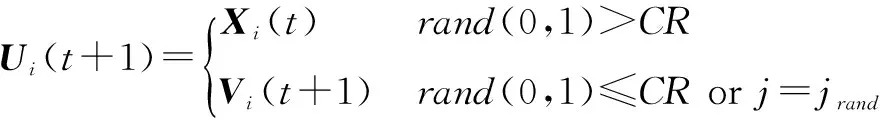
(11)

式(1)中：rand(0,1)取0～1之间的随机数；CR为确定交叉概率，取0～1之间的实数；jrand的取值为1～n(n=8)之间的自然数。这就保证了Ui(t+1)向量至少有一个分量来自目标向量。

④选择操作。

(12)

通过执行步骤②～步骤④的循环操作，可得最大进化代数。

⑤选择Pareto最优解。

建立初始为空的非支配集Y，将产生的非支配解存放在Y中，并将产生的可行解Xi(t+1)与Y中的向量作比较。如存在支配关系，就删除该支配解，将非支配解存入Y中，直到满足结束条件。最终，最优解都在Y中[8-9]。

3　实例仿真与分析

3．1　实例条件

从一个配送中心出发，为了满足8位顾客的配送要求，用1～8分别对顾客进行编号。用0表示配送中心，采用同一型号车辆来配送物品。车辆最大载重质量为2 000 kg，平均行驶速度60 km/h。顾客配送时间要求及所需物品质量如表1所示。车辆从配送中心的出发时间为上午7∶00；顾客(含配送中心)之间的距离如表2所示。

表1　顾客配送时间要求及所需物品质量Tab.1　Delivery time requested by customers and the weight of the goods

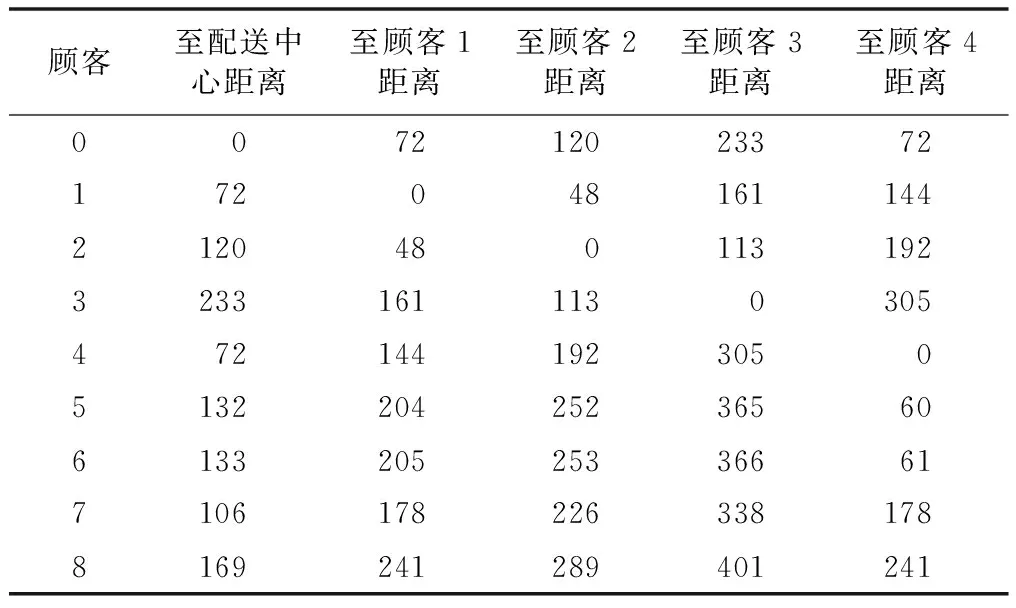
表2　顾客(含配送中心)之间的距离Tab.2　Distance between customers (including the distribution center)　km

3.2　仿真过程分析

整个仿真过程采用了3组起始种群数NP和迭代次数N∶NP=6,N=10；NP=10,N=10；NP=20，N=100。

表3为NP=6时随机产生的初始化种群，车辆数最多为6辆、最少为5辆，总运输路程最长为1 301 km，最短为932 km，平均为1 180 km左右。这些初始化种群的可行解离最优化较远。

表3　初始化种群(NP=6Tab.3　Initialization population (NP=6)

表4为NP=6时，经过十次迭代运算后的可行解集。从表4中可明显发现车辆运输总路程和配送车辆数都有了减少，最短总路程数为862 km，车辆数最小为3辆。

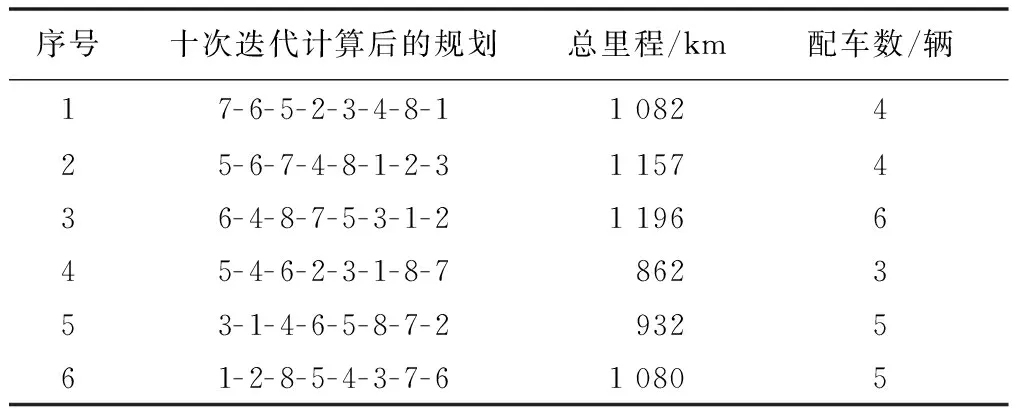
表4　十次迭代运算后的种群(NP=6)Tab.4　The population after ten generation operation (NP=6)

表5为当NP=10时，经过十次迭代运算后的最优可行解。表5数据表明，最优配车数为3辆，最短总运输路程为862 km，产生的3条规划路径为：5-4-6，2-3，1-8-7。

表5　十次迭代运算后的最优化解(NP=10)Tab.5　The optimal solution after ten generation operation (NP=10)

表6为当NP=20时，经过百次迭代运算后的最优可行解。表6数据表明，最优配车数为3辆，最短总运输路程为799 km，产生的3条规划路径为：5-4-6，2-3，1-7-8。

表6　百次迭代运算后的最优化解(NP=20)Tab.6　The optimal solution after one hundred generation operation (NP=20)

4　结束语

VRP问题一直是大家关心的重要课题。研究者从不同的角度对其展开了研究与应用，取得了不少成功的案例。带有时间窗口的VRP问题相对较复杂，受到更多的约束条件限制[10]。本文采用了适当改进的差分进化算法，对物流配送中的多目标优化进行了应用研究，MATLAB仿真结果表明，算法可行、有效，收敛快且稳定，为物流配送规划提供了一种优化方案。(

参考文献:

[1] 邹霞玲.基于物联网的航空物流管理系统研究[J].自动化仪表，2016,37(6)：66-70.

[2] 杨振宇.差分进化算法参数控制与适应策略综述[J].智能系统学报，2011(10)：415-423.

[3] 蔡浩原.基于人工蜂群算法的鲜活农产品冷链物流配送路径优化[J].江苏农业科学，2017(15)：318-321.

[4] 杨启文.差分进化算法综述[J].模式识别与人工智能，2008(4)：506-513.

[5] 裴振奎.差分进化算法在多目标路径规划中的应用[J].辽宁工程技术大学学报，2010(5)：899-902.

[6] 李伟.基于时间最短路径的停车场车位引导算法[J].自动化仪表，2015,36(8)：23-25.

[7] 徐杰.基于混合粒子群算法的多目标车辆路径研究[J].计算机集成制造系统，2007(3)：573-580.

[8] 李昌兵.物联网环境下生鲜农产品物流配送路径优化研究[J].商业研究，2017(4)：1-9.

[9] 李荣雨.改进的差分进化算法在电力经济调度中的应用[J].自动化仪表，2016,37(11)：43-47.

[10]虎涛涛.一种混沌变参数粒子群优化算法[J].自动化仪表，2017,38(3)：37-40.