基于参数估计的下视稀疏阵列三维SAR运动误差补偿和成像处理方法

刘奇勇 张 群 洪 文 苏令华 梁 佳

①(空军工程大学研究生院 西安 710077)

②(空军工程大学信息与导航学院 西安 710077)

③(信息感知技术协同创新中心 西安 710077)

④(复旦大学电磁波信息科学教育部重点实验室 上海 200433)

⑤(微波成像技术国家重点实验室 北京 100190)

⑥(中国科学院电子学研究所 北京 100190)

1 引言

3维合成孔径雷达(3-Dimensional Synthetic Aperture Radar， 3D SAR)成像能够克服传统2维SAR成像中存在的阴影和重叠效应[1]，获得场景的3维成像结果[2-4]。与其他的3D SAR成像技术相比，例如：层析SAR成像[5]、干涉SAR成像[6]等，阵列3D SAR成像技术通过单次航过就能得到场景的3维图像[7-10]，而且成像模式更加灵活，尤其是稀疏阵列下视3D SAR(Downward-Looking Sparse Linear Array 3D SAR， DLSLA 3D SAR)成像能够克服斜视中存在的阴影效应，得到了更加广泛的关注。

DLSLA 3D SAR系统的线阵长度受限于平台的尺寸，导致跨航向分辨率比较低，很多文章对提升DLSLA 3D SAR系统的跨航向分辨率进行了研究[11，12]。但是这些文章并未考虑载机飞行不理想的情况，实际情况下，载机的运动是会存在误差的。为补偿运动误差，文献[13]提出一种基于波数域的运动补偿方法，但是该方法需已知载机的运动参数。文献[14]提出一种基于多通道联合自聚焦的方法，该方法利用传统图像偏置(map drift)法实现图像的自聚焦，但是没有考虑多普勒调频空变的特点。事实上，DLSLA 3D SAR成像与传统的SAR成像中的运动误差补偿是存在不同的。传统SAR一般都是远距离成像，方位向合成孔径较长，合成孔径时间也比较长[15，16]。但是，DLSLA 3D SAR成像中，由于跨航向分辨率与平台高度成反比，要使其跨航向分辨率在可接受的范围内，载机平台的高度就不能太高，合成孔径长度也就不会太长，合成孔径时间也会较短。因此，在一个合成孔径时间内载机一般都可看成是平稳飞行的。

基于以上分析，本文研究载机飞行过程中存在偏航角速度时的DLSLA 3D SAR成像。首先建立载机存在偏航角速度下的DLSLA 3D SAR成像模型；其次，通过理论计算得到多普勒调频率的显示表达式，并且多普勒调频率与散射点被调制后的跨航向坐标有关，而与被调制后的方位向坐标无关；因此，可以先处理跨航向信号，再处理方位向信号；接着，在完成跨航向信号重构后，在平台运动参数存在误差的情况下，基于参数化稀疏表征方法实现了平台的速度和偏航角速度的估计，进一步利用所得到的参数构造方位补偿函数完成了方位向信号的处理，实现了运动误差的补偿；随后提出一种形变校正方法。仿真实验验证了所提算法的有效性。

2 DLSLA 3D SAR成像运动误差建模

DLSLA 3D SAR成像几何模型如图1所示。假设飞机以速度v平行于X轴(方位向)飞行，飞行高度为H。稀疏线性阵列布设在机翼下方，沿着Y轴(跨航向)排列，并且关于高度向Z轴(距离向)对称。阵列结构为两端的为发射阵元，数量为，间隔为2d，中间的为接收阵元，数量为，间隔为，则通过等效相位中心(Equivalent Phase Center，EPC)原理，可以得到等间隔的均匀EPC，数量为，间隔为d。发射阵元采用时分的工作模式发射信号，则在利用EPC原理时，会引入双基等效为单基的距离误差同时不同时刻的EPC不在同一直线上，需要补偿运动引入的EPC误差，经过EPC误差和运动引起的EPC的误差补偿后，就可以利用EPC直接对信号处理[17]。由于发射阵元为偶数，因此，等效的EPC数量N也为偶数，实际上，在该阵列结构中，阵列的中心没有EPC，因此，可把该点看成均匀EPC丢失的点，并将其添加到EPC中，并EPC从左至右依次编号，并组成序列向量，而EPC稀疏采样得到的序列为，每个采样序号p对应着EPC的序号为，那么对于第p个降采样的EPC，其在慢时间时刻的坐标可以表示为，其中，为慢时间的全采样序列。当机载平台存在偏航角时，载机的实际航线为图中实线所示，则第p个等效阵元到第k个散射点的实际的瞬时距离如式(1)所示。

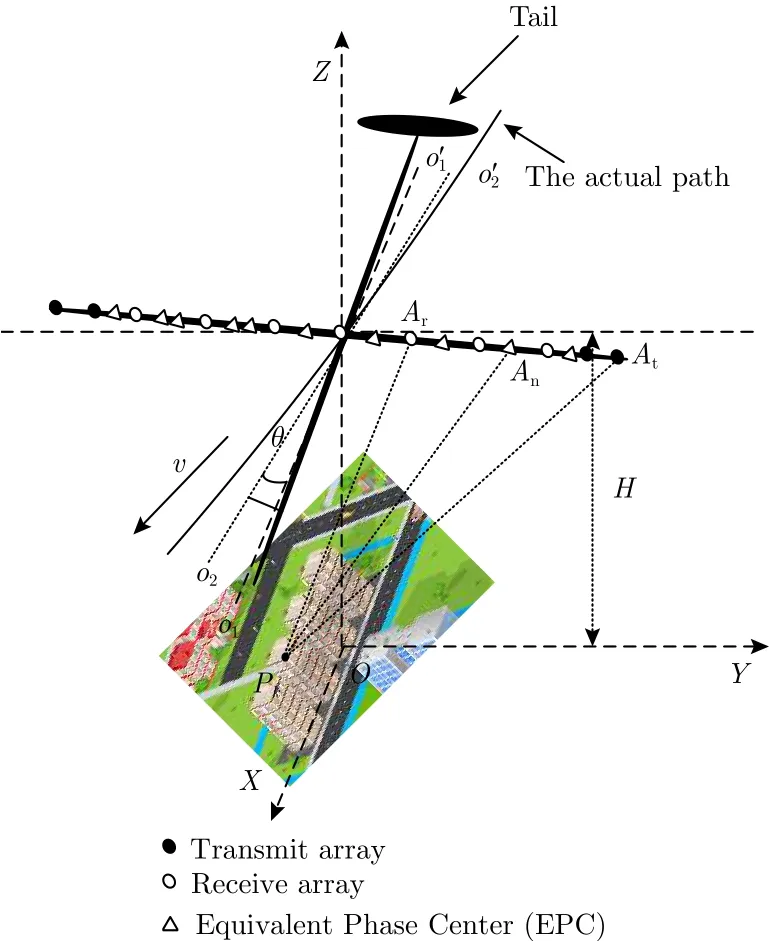
图1 DLSLA 3D SAR成像几何模型Fig. 1 DLSLA 3D SAR imaging geometry model

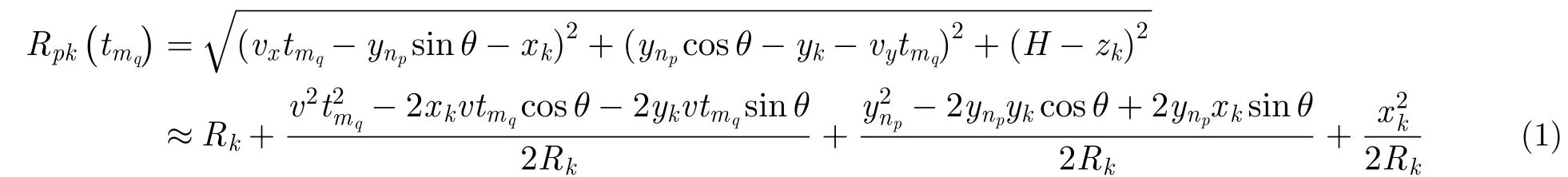
载机在运动过程中，偏航角变化呈正弦形式，而且，最大偏航角一般不会太大，会被控制在一定范围内。在该条件下，载机的偏航角变化可以近似成线性变化。基于此近似，假设偏航角速度为，初始偏航角为，则瞬时偏航角为。根据瞬时距离的表达式，可得瞬时多普勒

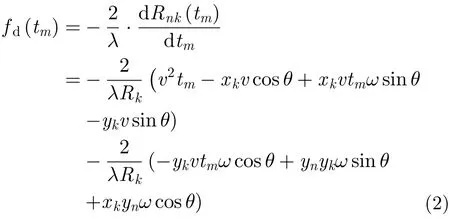
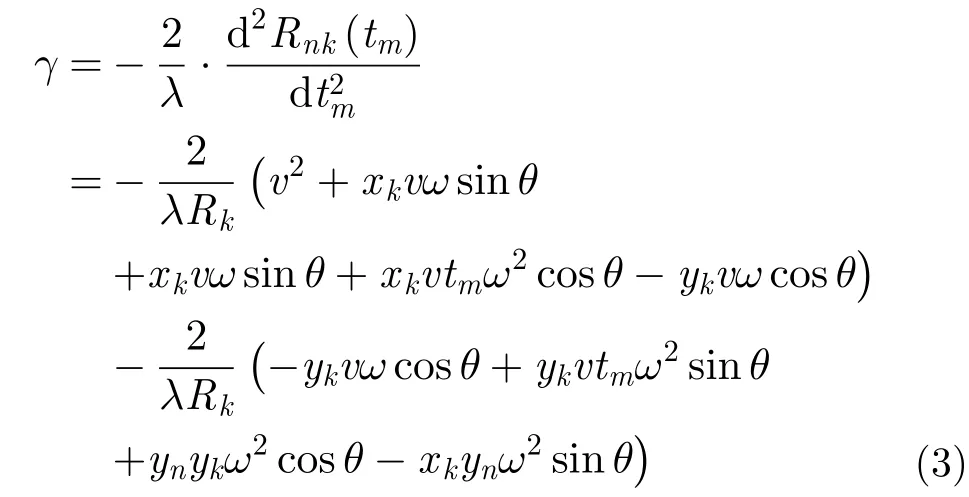
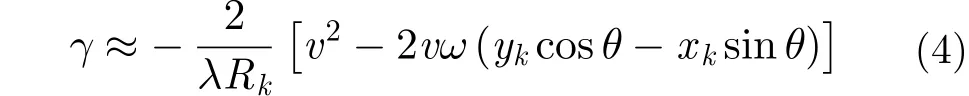
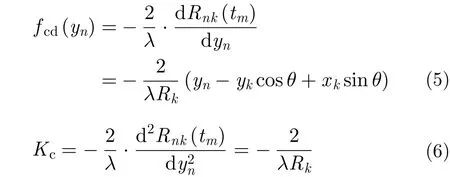
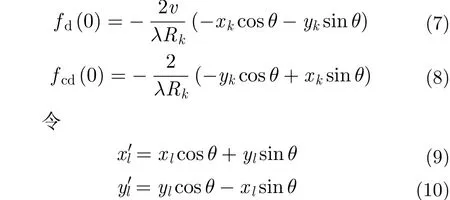
由式(7)-式(10)可知，第l个散射点在方位维-跨航向维平面聚焦后的位置为，而不是，即散射点（的方位向坐）标和跨航向坐标被调制了。且。则信号完成距离压缩后，第i个距离单元对应的方位向-跨航向2维信号可表示为

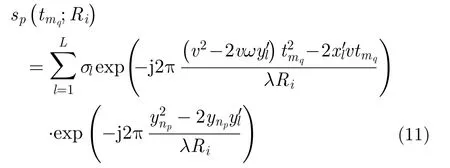
3 基于参数化稀疏表征的平台参数估计方法

完成距离压缩和跨航向信号重构后，位于第i个距离单元、第l个跨航向单元的方位向信号可表示为

根据式(13)，方位向稀疏字典可构造为

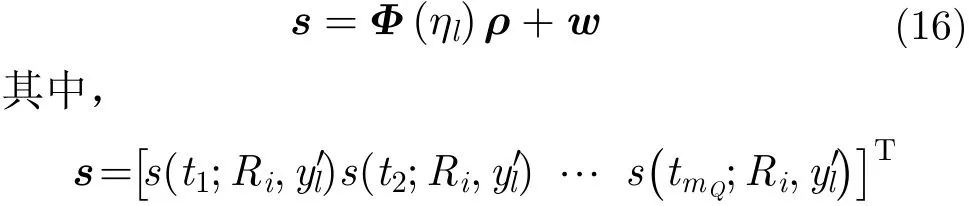
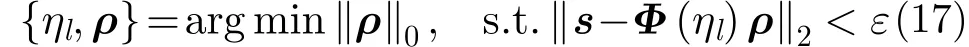
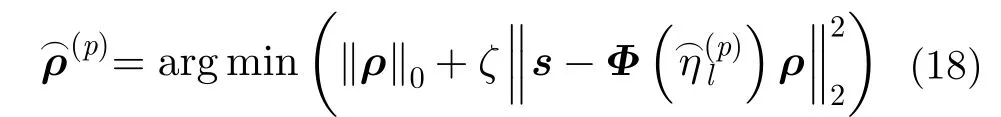
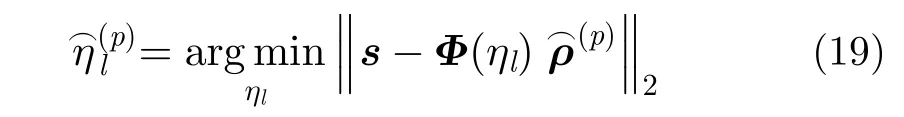
式(22)可利用最小二乘法求解，进而，参数可以利用式(23)进行更新。

4 形变校正

由于聚焦后的3维图像在方位向-跨航向平面存在形变，因此，需对各个高度维的方位向和跨航向平面进行形变校正。

首先，根据方位向处理之前的信号，可得第k个散射点的回波起始时间或者回波终止时间。

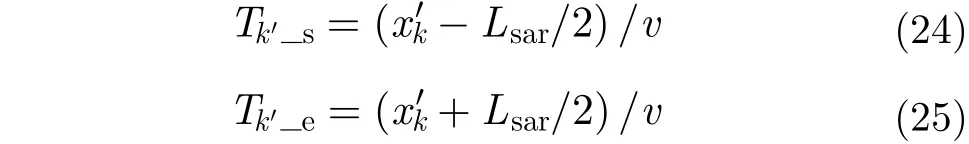
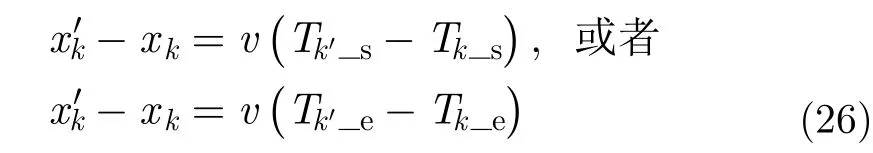
根据式(9)、式(10)和式(26)，可计算出散射点的准确坐标，并且估计出初始偏航角的值。在完成形变校正之后，就能得到准确的3维场景图像。

本文所提算法的完整流程图如图2所示。

5 仿真实验和分析

本节利用仿真数据和DEM数据来验证本文所提方法的有效性。

5.1 DLSLA 3D SAR成像孤立点目标实验

首先进行孤立点目标仿真实验。点目标模型如图3所示，所有点目标的反射系数均设为1。当载机的飞行速度为60 m/s，所得到的阵列尺寸为4.3 m×1.0 m(阵列方向×方位向)，为保证方位向信号不出现模糊，脉冲重复频率至少为120 Hz；由于DLSLA 3D SAR成像系统采用MIMO时分工作方式，因此，跨航向信号需要16个脉冲周期才能得到一个全孔径的EPC，则系统的脉冲重复频率至少为1920 Hz。为了在较短的合成孔径时间内采样足够的信号，系统的脉冲重复频率设为5000 Hz。实验仿真参数如表1所示，EPC之间的间隔设为半个波长，载机平台存在偏航角运动误差。

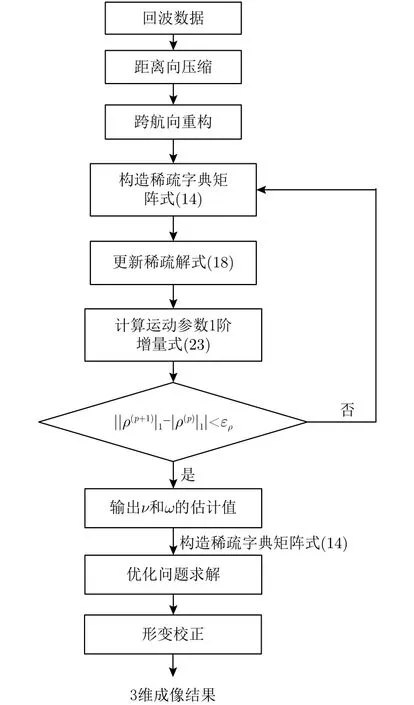
图2 所提方法流程图Fig. 2 The flow chart of the proposed method

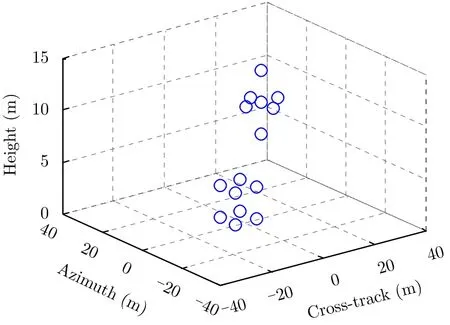
图3 3维孤立点目标模型Fig. 3 3D isolated targets model

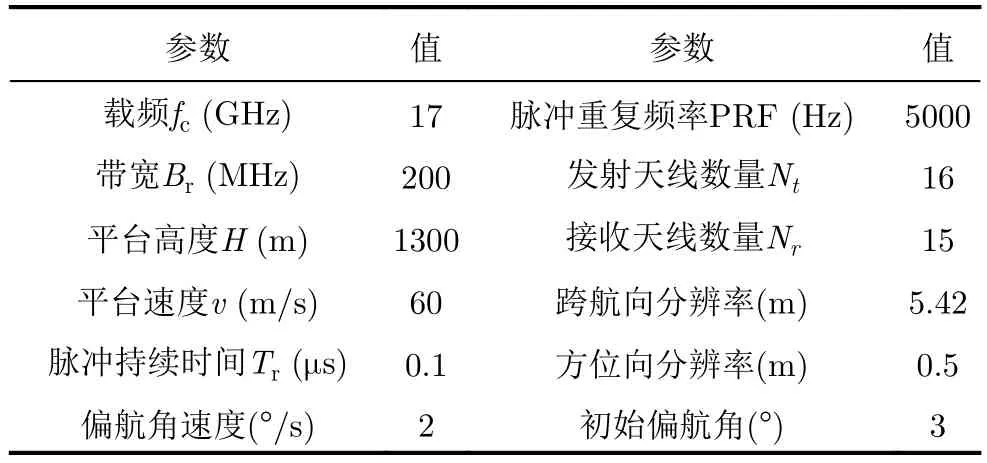
表1 平台和天线的参数Tab. 1 Parameters of platform and antenna

仿真实验中，假设平台自身的速度和偏航角速度估计值的误差分别为2 m/s和2°/s，并且在距离压缩后的信号中加入噪声，使得到的信号的信噪比为5 dB，跨航向利用波束形成原理对信号进行压缩。方位向的降采样率为0.8，图4(a)为直接构造稀疏字典矩阵对信号进行重构后得到的3维成像结果，此处称为直接成像方法，可见，方位向仍然存在展宽现象，方位向信号采用迭代阈值法进行重构。这是因为平台的运动参数值不准确，导致所构造的方位向稀疏字典矩阵与理想的稀疏字典矩阵不完全匹配。进一步，利用所提出的参数化稀疏表征方法估计平台的运动参数，得到平台的速度和偏航角速度的估计结果分别为60.08 m/s和2.09°/s，再根据得到的运动参数构造方位向稀疏字典矩阵对信号进行处理，成像结果如图4(b)所示，可见，方位向聚焦效果良好。这说明所提的参数化稀疏表征方法能够准确估计平台的运动参数，并完成方位向信号处理，实现平台运动误差的补偿。

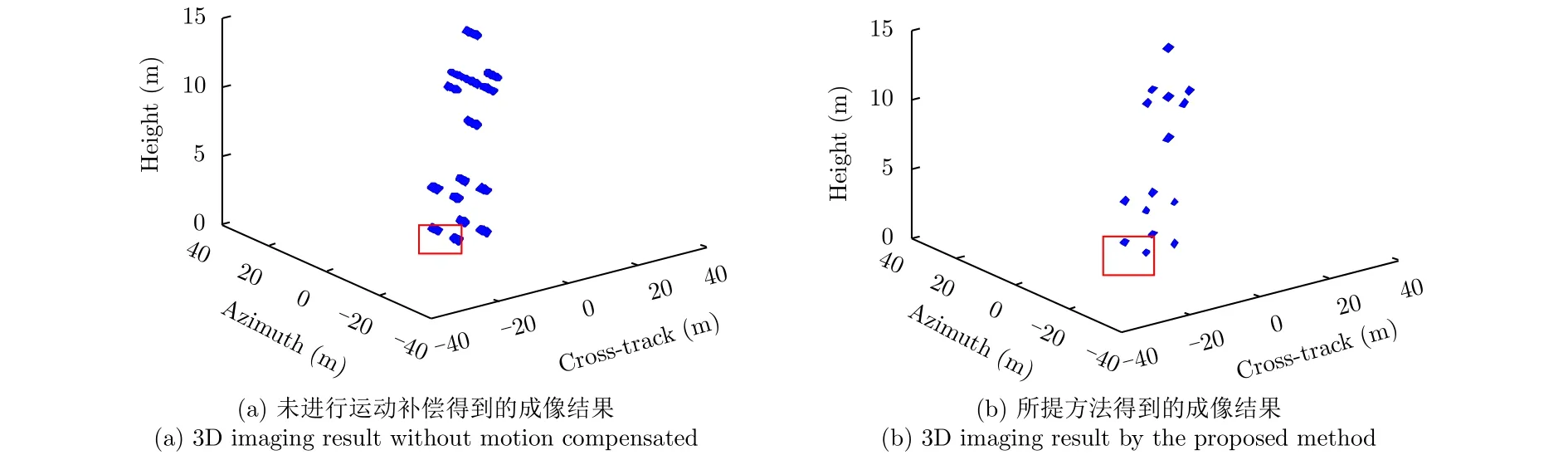
图4 成像结果Fig. 4 Imaging result

图5 为图4(a)和图4(b)红色矩形区域内两个目标的方位向截面图，图5中红色线条代表图4(b)对应的方位向截面图，蓝色线条代表图4(a)对应的方位向截面图，可见，基于参数化稀疏表征的方法能够实现方位向的压缩，而直接法由于采用的平台运动参数不准，导致构造的稀疏字典与信号不匹配，因此存在一定的展宽现象。表2为图5中两种方法对应的3 dB宽度。其中提升倍数的定义为：直接法的3 dB宽度/参数化稀疏表征法的3 dB宽度。可见，所提方法的聚焦效果有明显的改善。

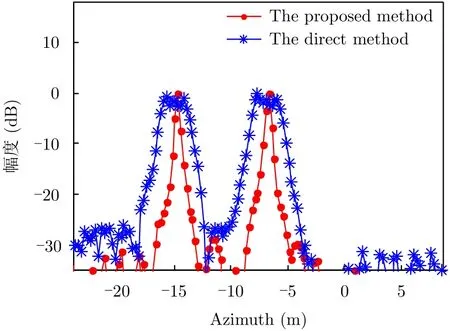
图5 方位向截面图Fig. 5 The azimuth sectional image

表2 图5中两种结果对应3 dB宽度Tab. 2 The 3 dB width of the two methods in Fig. 5

因此，接下来分析图像的形变校正问题。图6(a)为图4(b)在方位向-跨航向平面上的投影结果，可见，聚焦所得散射点坐标的方位向坐标和跨航向坐标与其真实值确实存在偏差，而且矩形区域内目标坐标的偏差比椭圆形区域内的目标坐标的偏差更加严重。这可从方位向坐标和跨航向坐标被调制的公式看出，当目标的真实坐标越大时，坐标受到调制的影响也越严重。图6(b)为经过形变校正之后的结果，通过将图6(b)与图6(a)进行对比可以发现，校正后目标所在的位置与其真实值非常接近，而且不同区域的图像所发生的形变都能够得到准确的校正。即所提形变校正方法是有效的，利用所提方法能够校正图像所产生的形变。并且，根据形变校正方法得到的初始偏航角为2.92°。

进一步，得到图6(b)中所示的5个目标形变校正前后的坐标，如表3所示，表明所提形变校正方法是有效的，利用本形变校正方法对图像进行处理能够明显改善图像性能。

5.2 DLSLA 3D SAR成像分布式目标仿真

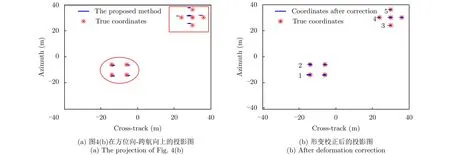
图6 方位向-跨航向平面投影图Fig. 6 2D projection onto azimuth and cross-track plane

表3 形变校正前后的方位向、跨航向坐标Tab. 3 The azimuth and cross-track coordinates before and after deformation correction

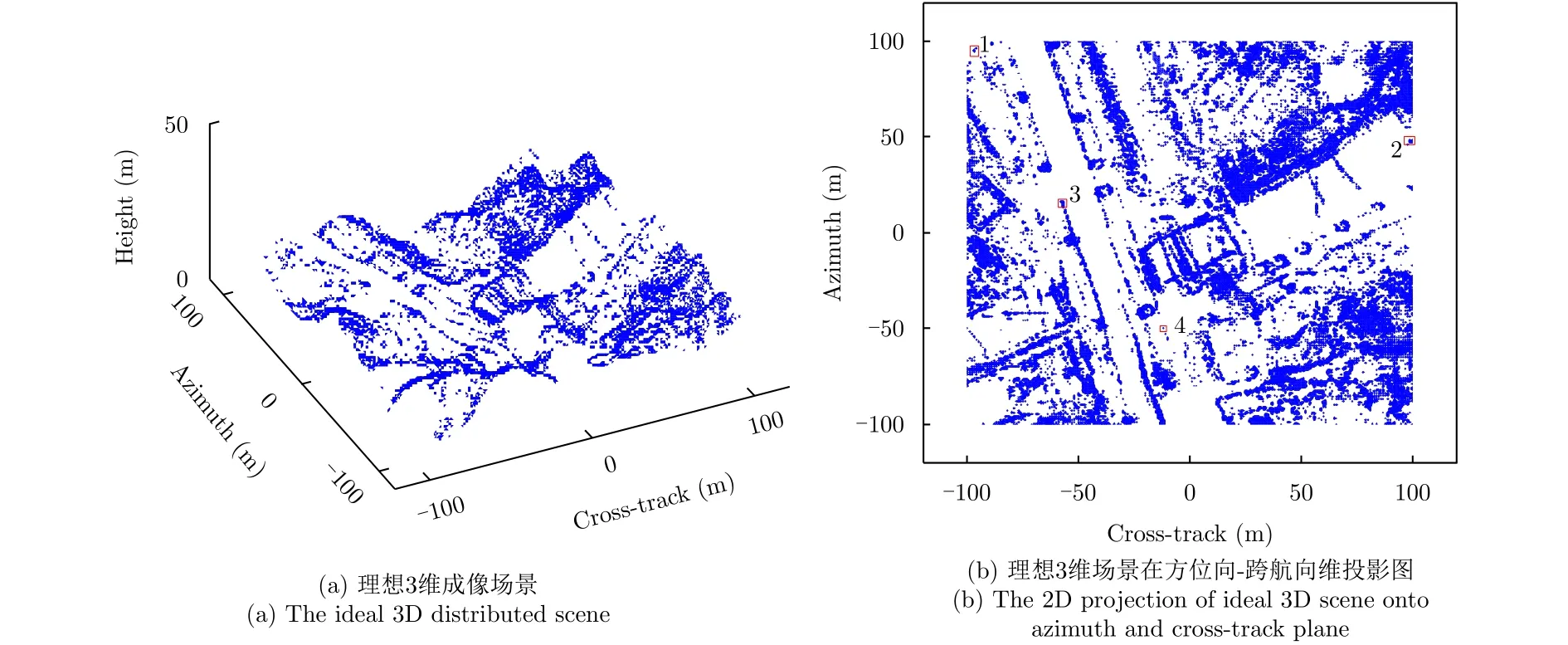
图7 成像场景示意图Fig. 7 The ideal scene

在本节仿真实验中，分布式场景及其在方位向-跨航向平面上的投影图分别如图7(a)和图7(b)所示。仿真参数如表1所示，在笛卡尔坐标系中，仿真场景的大小为200 m×200 m×35 m。散射点的方位向坐标均匀分布在[-100 m， 100 m]，间隔为1 m。散射点的跨航向坐标均匀分布在[-100 m， 100 m]，间隔也为1 m。根据系统参数，可算出跨航向的瑞利分辨率为5.42 m。为了评价所提算法的抗噪性能，在距离压缩后的信号中加入噪声，使信号的信噪比为5 dB，跨航向利用波束形成原理对信号进行压缩。在进行仿真时，方位向重构时的降采样率设为0.8。假设平台自身的速度和偏航角速度估计值的误差分别为2 m/s和2°/s，方位向信号采用迭代阈值法进行重构，由本节所提方法得到的场景3维成像结果如图8(a)所示，图8(b)为未进行运动误差补偿得到3维成像结果。从图8(b)可以看出，未进行运动误差补偿的成像结果中存在一些细节丢失的现象，而所提的方法能够得到完全聚焦的3维图像，平台的速度和偏航角速度的估计值分别为59.91 m/s和2.06°/s。进一步，得到图8(a)和8(b)在方位向-跨航向2维平面上的投影结果，分别如图9(a)和9(b)所示。从图8可见，两种方法得到图像在方位维-跨航向维平面都发生了形变，而且图9(b)还存在展宽现象。最后，根据所提形变校正方法，图9(a)经过形变校正后得到的结果如图10所示，可见，图像的形变得到了校正，并且偏航角的初始值的估计值为3.06°。即本文所提方法对分布式场景也是有效的。

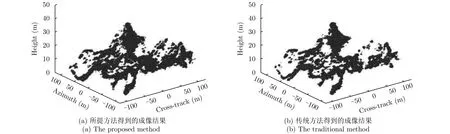
图8 分布式场景DLSLA 3D SAR成像结果Fig. 8 3D imaging result of scene

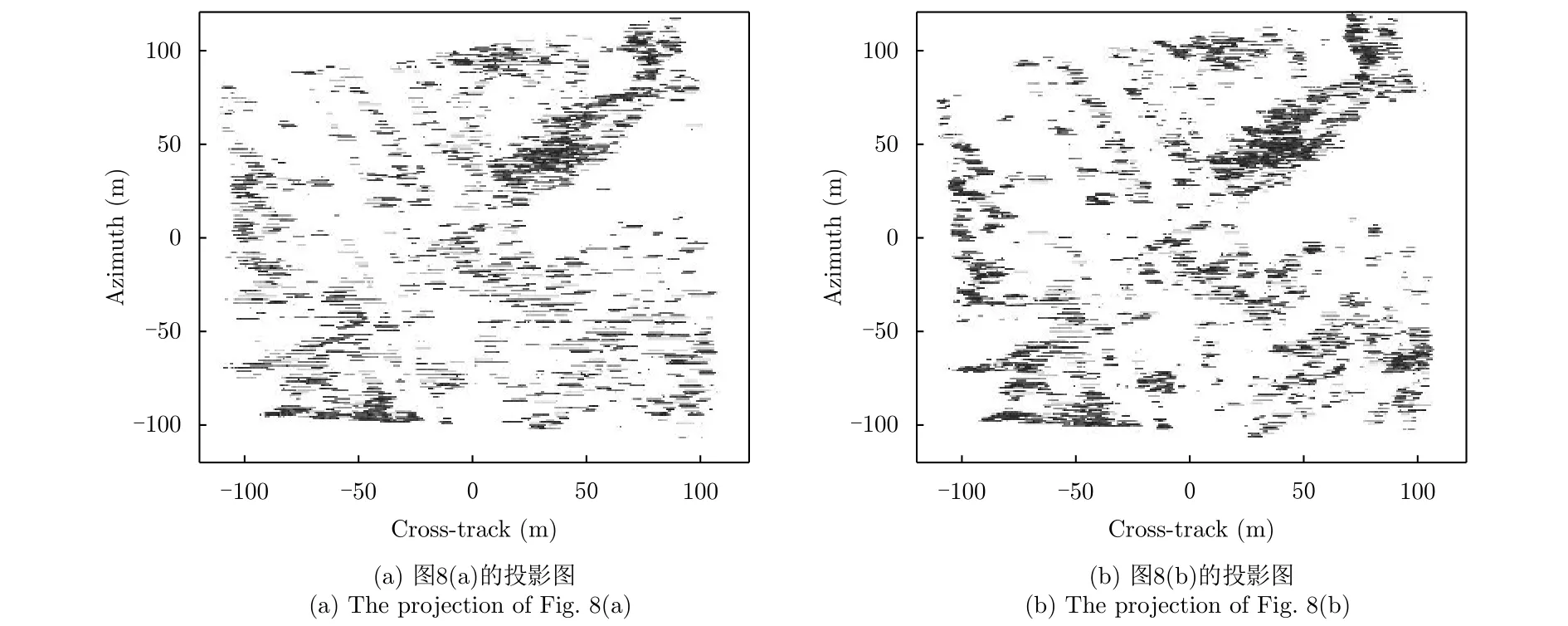
图9 方位向-跨航向平面投影图Fig. 9 2D projection onto azimuth and cross-track plane

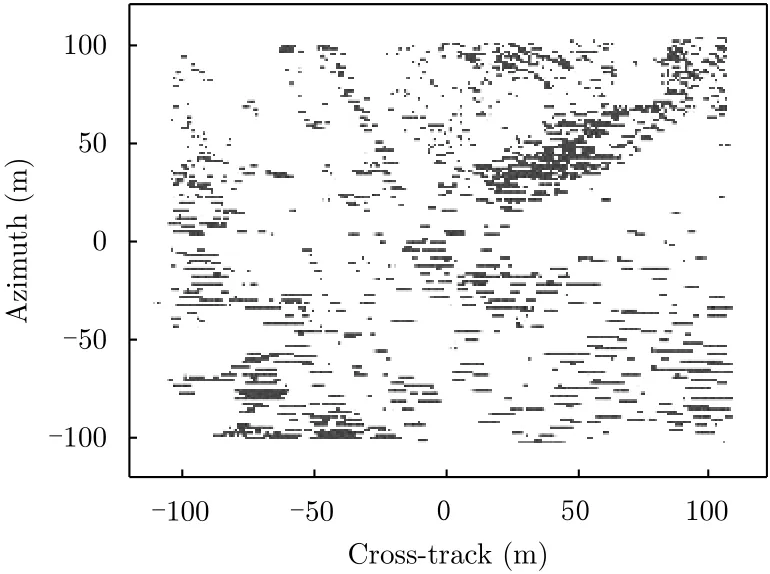
图10 形变校正后的方位向-跨航向平面投影图Fig. 10 2D projection onto azimuth and cross-track plane after deformation correction.

进一步，为评价形变校正方法对分布式场景的校正性能，得到了理想场景图7(b)中标示出的4个目标形变校正前后的方位向、跨航向坐标，如表4所示。提升倍数的定义为：|实际坐标值-校正前的坐标值|/|实际坐标值-校正后的坐标值|。可见，形变校正后的坐标相比校正前的坐标得到了很大的改善。即本形变校正方法对分布式场景也有效。

6 结论

DLSLA 3D SAR成像在载机存在偏航角速度的情况下会对成像产生影响。当载机存在偏航角速度时，信号多普勒调频不仅与平台的速度和偏航角速度有关，还与被调制后的跨航向坐标有关，而与被调制后的方位向坐标无关。因此可以先处理跨航向信号得到目标被调制后的跨航向坐标，再处理方位向信号。本文所提基于参数化稀疏表征的方法能够实现平台速度和偏航角速度的估计，并完成方位向信号重构，所提的形变校正方法能够校正图像的形变。仿真结果验证了本文所提方法的有效性。

表4 形变校正前后的方位向、跨航向坐标Tab. 4 The azimuth and cross-track coordinates before and after deformation correction