学生说题在试卷讲评课的案例研究
2018-04-16兰伟红
兰伟红
试卷讲评课,尝试以学生为主角,让学生确定评讲题目,说题目特征,说命题意图,说解法和困惑,说解后反思,老师只是在学生疑难处适当点拨,会起到老师讲学生听的被动学习模式所难以达到的效果。本文以我校高二期末试卷讲评为例,具体阐述学生说题实践活动,望各位同仁指正。
一、聚焦似曾相识题
一份数学试卷22题,难易度不等,特别容易或特别难的都不适合在课堂上由学生讲解,大家最感兴趣最愿意分享交流的是一些看上去会做,实际却做不出来或做不完整,甚至对自己的错误做法浑然不知,倍感纳闷的试题。期末数学试卷一道填空题:设数列的前n项和Sn,若,学生的答题情况大体有三种:1365,1024,空白,统计显示出错率68.7%,而且在公布答案后仍有不少同学坚持认为第一种答案才是正确答案,因为他们用两种不同的解法都得到了同一个结果。课代表在试卷讲评课的前一天征集说题对象时,各组同学异口同声地要求说说这道题。如此,这题脱颖而出。
二、小组研判题后意
解好一道题,要从字里行间揣摩出命题者出题意图——考查哪块知识点,何种解题方法和思想。如此,才能比较快速地反映出相关知识点,想起关联题型的典型解法,为思考解决问题找到思路和方向。针对此题,我要求各小组讨论命题者出题意图,并形成文字作为第二天课堂上学生说题的讲话稿。经过小组同学重新认真思考,交流汇总得出命题者出题意图:1.考查通项与前n项和的关系 ;2考查递推关系的应用或等比数列的判定与通项或前n项和的计算。在交流讨论中,有的同学颇感后悔:这些知识点我咋想不起来呢?同时也燃起希望:及时消化巩固好知识点就能入手解题。有的仍紧锁眉头,苦思冥想;有的已恍然大悟,充当起小老师;有的却与同学争的面红耳赤……学生的学习热情得到充分点燃,数学知识数学方法在学生脑海中互相碰撞和交流……
三、五花八门亮解法
在课前五分钟,各小组代表把同学中的典型解法已展示在黑板上了:
学生1的解法:∵an+1=3Sn∴a2=3 S1=3,同理:a3=3S2=3(a1+a2)=12,a4=3S3=48,a5=3S4=192,a6=3S5=768,
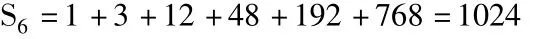
学生3的解法:∵an+1=3Sn∴an=3Sn-1,得的等比数列。
四、拨云见日辩真伪
在试卷讲评课中,老师简短分析学生成绩和试卷答题情况后,时间就交由学生说题支配了。
同学4:由an+1=3Sn我猜测本题意图是考查前前n项和概念和递推关系。由a1=1,an+1=3Sn算出a2=3 S1=3,反复运用可依次算出a3,a4’a5’a6’从而求出 S6。
同学5:我也是这么算的,心里还暗喜:幸好求的S6,如果求S100就完蛋了!看来还要回归更一般的方法!
同学6:我想到了通项与前n项和的关系 ,但在做到Sn+1=4Sn这一步时,由于平时对概念辨析不清,我就稀里糊涂地写上q=4的等比数列,造成了解法二的失误!
同学7:我们平时学习一定要充分理解概念。由Sn+1=4Sn应得出是等比数列,且,进而求出这里 S6不是数列的前六项的和,而应该是数列的第六项。概念清楚就不会在关键时候犯糊涂!
同学8:有道理!不能被外在形式所迷惑!但是解法三我现在都还整不明白,错在哪儿了?概念和公式我都记得清清楚楚的,没问题呀!
同学9:由 an+1=3Sn得 an=3Sn-1,这一步似乎漏了限制条件,应添加n>1的条件,否则Sn-1在n=1时没意义了。
同学10:对!这个条件必须加上!会不会就是这个条件的缺失导致结果有问题呢?
同学们陷入一片沉思中……
看到火候已到,一直在倾听的我发言了:解法3中两步有问题,第一步∵an+1=3Sn∴an=3Sn-1中漏了限制条件:n>1,这一点同学已发现了,点赞一个!那第二步错在哪儿呢?在“由an+1=4an得出是的等比数列”中有问题!大家想一想:n>1时,由能否得出是等比数列?
同学11:老师,我知道了!n>1时,an+1=4an不能说明第二项与第一项的关系,进而不能满足等比数列的概念:从第二项起,若每一项与前一项的比是一个定值,则这个数列是等比数列。
同学一片惊呼:是呀!我们忽略了“n>1时”对“an+1=4an”结果的影响。
此时此刻,同学们不由自主地鼓起掌声,为同学的精彩讲解,为自己的恍然大悟……
五、反思得失长智慧
学生13:重视数学概念的学习,领悟其本质含义,能避免形式错误,更能准确界定数学结论,如解法是除a1外的等比数列,即首项是 a2=3,公比 q=4。
学生14:在类比构造数学等式的时候,一定需关注限制条件的变化,养成严谨认真的习惯。
六、变式训练促提高
是等差数列。
结束语:以上是我们在试卷讲评课中开展学生说题应用的一个案例。课堂中学生思考解决问题的思路历程得以全景展示,学生据此思辨交流,感悟真知灼见,激发了学习的兴趣和热情,提高了思考问题解决问题的能力,发展了数学核心素养。学生说题值得在试卷讲评中大力推广!
参考文献:
[1]林建森“说题”在(高中数学)习题教学中的运用;《高中数学教与学》2013年第7期
[2]陈启南 高三数学试卷讲评课开展说题活动的实践与感悟;《中国数学教育》2014年第1-2期
