高分子聚合物热输运调控的研究进展

董岚，张颖 ，徐象繁 ∗

1同济大学物理科学与工程学院声子学与热能科学中心，上海

2同济大学中欧纳米声子学联合实验室，上海

I.引言

在过去的半个多世纪里，半导体技术快速发展。高密度集成芯片在智能手机、电脑、飞机和航天科技等领域有着广阔的应用前景，是世界各大国争相攻克的战略高地。目前普遍采用的22纳米晶体管集成电路在厘米大小的芯片上集成了数十亿个晶体管。如此高密度的晶体管在工作时最大可产生100W/cm2的热量[1]。这些高密度热量集聚在狭小的器件空间内，如果不能及时传导出去，必定会在芯片局部产生高温（即通常说的热点），影响芯片正常工作，严重时可导致器件烧毁。因此，解决芯片的散热问题并使器件工作在较低温度已成为科研工作者需要解决的首要问题[2,3]。

芯片散热大致可分为两个过程，如图1a所示。首先是热量从单个晶体管传导至封装外壳。其次是通过多种介质（如散热片或冷却水）将热量传导到环境中，如计算机普遍采用空气为介质，利用风扇和金属散热片将热量传导至环境中；手机采用高热导碳膜为导热介质；大规模计算机服务器采用微槽冷却(microchannel cooling)的方式；手持式红外相机等采用热电制冷 (thermoelectric cooling)。

热量从单个晶体管传导至封装外壳还可以细分为两个步骤。第一步是热量在集成电路内部传递。这一步涉及到热量在纳米尺度内的传递过程，以及热量如何通过微电子器件之间的界面。由于微电子器件是由半导体材料制成，而在半导体中声子是热量的主要载体，因此这一问题变成了声子如何在纳米尺度内传播，以及声子如何通过各种界面。声子的特征长度通常只有几个纳米到几百纳米之间，同时所有声子的振动模式都对热传导起作用(电导体中，只有费米面附近的电子对电传导起作用)，这使得对微纳尺度声子热传导的研究面临来自理论和实验的双重困难。这也导致了对其研究还处在基础研究阶段，且尚未在工业界得到有效应用。关于微纳尺度声子热传导研究及其相关调控问题，可参考相关文献[4−7]。

第二步是集成电路上的热量通过热界面Ⅰ和热界面Ⅱ传递至封装外壳，其中热界面Ⅰ为集成电路与封装外壳的界面，热界面Ⅱ为封装外壳与散热器之间的界面。需要特别指出的是，热界面Ⅰ和热界面Ⅱ是微观与介观尺度下的界面，而上文提到的界面为纳米尺度，两者在热传递上有着本质的区别，因为在纳米尺度下，热传导基本方程（即傅立叶定律）已经不再适用。由于固体表面在微纳米尺度下存在一定的不平整度 (见图1b)，使得热量在热界面Ⅰ和热界面Ⅱ处只能从狭窄的接触点传导 (非接触处的空气热导率只有 0.02Wm−1K−1,几乎可以忽略不计)，这将使得器件散热能力大幅度降低。为解决这一问题，通常需要在热界面Ⅰ 和热界面Ⅱ处添加一层厚度为几个微米至几十微米的高热导热界面材料，以增加总界面热导。图1c为热界面材料导热示意图，其总热阻由两部分组成，即：

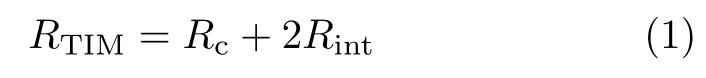
其中RTIM为界面总热阻，Rint为热界面材料与封装外壳及散热器之间的界面热阻，Rc为热界面材料自身热阻：

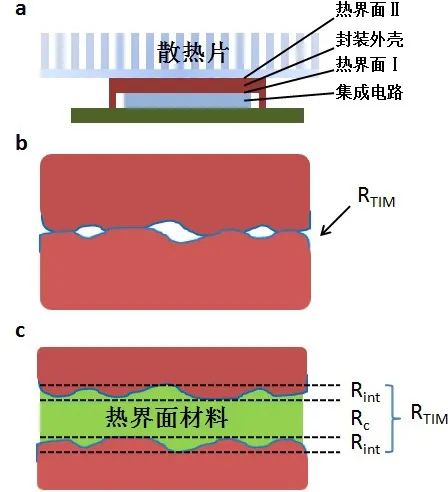
图1.a高密度集成电路散热示意图；b&c热界面材料示意图

其中κ为热界面材料热导率,t为界面材料的厚度。为增加界面材料与封装外壳及散热器热接触面积以降低界面热阻Rint，通常采用流体状材料作为热界面材料的原料，如目前最常用的环氧树脂。然而，包括环氧树脂在内的高分子聚合物材料为热绝缘材料，其热导率只有0.1—0.3 Wm−1K−1左右。因此，为降低热界面材料自身热阻Rc，通常会在聚合物中掺杂高热导纳米材料制成纳米复合材料，如金刚石颗粒、纳米碳管或者金属颗粒或金属线，以增加热传导效率。

目前科学家对于高分子聚合物及其相关纳米复合材料热传导机理的认知还十分有限，因此如何通过理论及基础实验来指导热界面材料的制备和调控是一个重要课题。对其导热机制理解上存在的困难主要有以下几点：

1.高分子聚合物基体材料的导热机制还不是十分清楚，目前已有实验和理论表明通过拉伸和应力增加聚合物内分子链的有序度可增加聚合物热导率；

2.聚合物与填料之间的界面对总热导率起削减作用，甚至可能主导其热传导，但对其具体效应在近几年里没有实质性进展。

因此，本文主要介绍聚合物基热界面材料的研究进展，重点介绍其热传导机理的相关理论与实验研究，指出当前研究存在的问题及今后可能的发展方向。

II.高分子聚合物热输运理论模型以及目前的研究进展

A.最小热导率模型 (MTCM)

1907年，爱因斯坦提出固体中原子振动可以看作是具有相同振动频率的，独立的简谐振子[8]。虽然爱因斯坦模型在解释晶体热导率时没有取得预期的成功，David G.Cahill与其合作者以爱因斯坦模型为基础提出的最小热导率模型[9,10]，普遍应用于分析无机非晶材料在高温时的热输运机制。随后Allen和 Feldman[11,12]基于数值计算分析了无序简谐固体中的振动模式与热输运，提出了 locons、diあusons和propagons三个概念用以区分无序结构中的振动模式以及不同振动模式对热传导的贡献。“locons”是局域化的振动模式，在简谐近似条件下locons对热输运没有贡献；“propagons”是声波振动模式与固体晶体中的声子类似；而无序结构振动模式中所占比例最大的是 “diあusons”，diあusons是非传播性的扩散振动模式，是无序结构中热能传播的主要承载方式。最小热导率模型假设非晶材料中的振动模式的寿命为τ=π/ω，基于德拜模型，热导率可用如下公式进行计算：

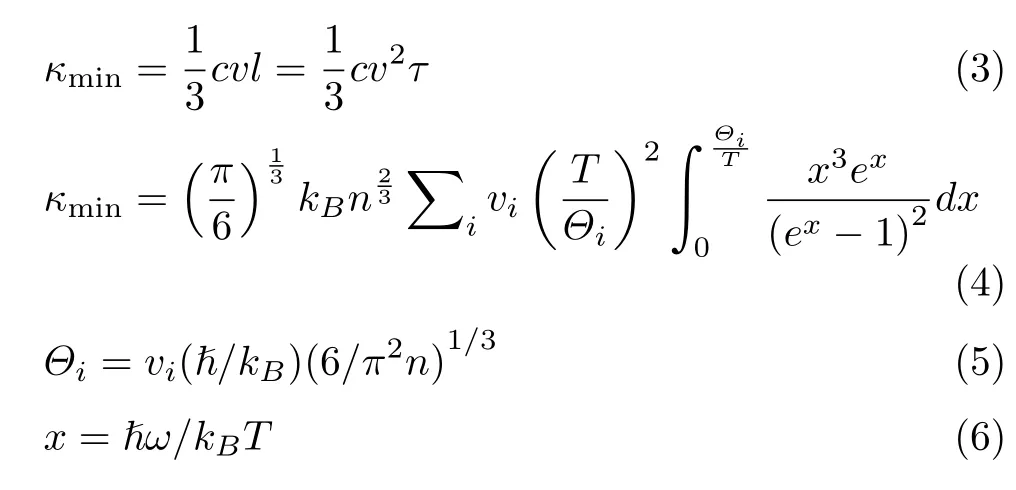
上述公式中考虑了三支声学模式（两支横向模与一支纵向模），vi表示每支振动模式的声速,κmin代表最小热导率，n代表单位体积内的原子数，Θi是德拜温度。

在高温极限下，所有的振动模式全部被激发，无序材料的最小热导率为：

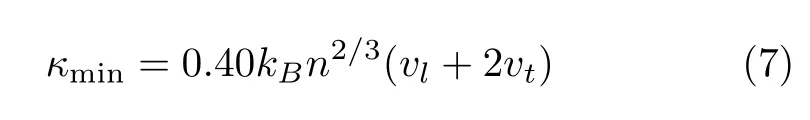
其中，vl和vt分别是纵向声学支与横向声学支的声速[8]。

近些年来很多研究者尝试将最小热导率模型应用于非晶的有机高分子材料中，借以解释高分子材料热输运机制[13,14]。2014年，Singh与其合作者对聚噻吩非晶纳米纤维热导率做了较为细致的表征工作[15]。在此研究中利用最小热导率模型描述了聚噻吩纳米纤维的热输运行为，并利用聚噻吩块材振动模的声速计算了纳米纤维的热导率。然而非晶高分子材料内部的分子链具有丰富的构象和聚集方式，分子链的这些特点是基于晶体的热导率模型没有考虑到的，因此在Singh的工作中能够看到理论值与实验值之间存在偏差。在晶格热容理论的发展中，德拜模型对晶格采取了一个简单的近似模型，把晶格当成各向同性的弹性介质来处理。这一假设使得最小热导率模型在非晶高分子有机材料中并不适用。高分子有机物中主链上各单元间以共价键的强相互作用相结合，链间则以范德瓦尔斯力的弱相互作用相结合，这使得高分子有机物体系是各向异性的弹性介质而并非理想假设中所讲的各向同性均匀介质，因此最小热导率模型在解释非晶高分子有机物的热输运性质时并不能很好地适配。这里值得指出的是非晶有机高分子链具有较强的非简谐性，而hopping模型[16]有望将这种非简谐相互作用对于热输运的影响一并考虑在内，但目前的研究工作尚未将hopping模型应用于解释有机高分子材料的热输运机制。

B.有效介质理论 (EMT)

有效介质理论是目前最普遍的估算复合材料热导率的理论模型。Maxwell-Garnett(MG)EMT[17]最早提出是为了计算复合材料的电导率，随后在计算复合材料热导率过程中证实MGEMT同样适用于复合材料热导率的计算。MGEMT假设填充粒子均以固定的随机球形粒子形式存在，并且填充粒子的体积分数被限制在很低的范围内[18]，以满足各球形粒子之间相互独立，不存在相互作用。基于以上假设，复合材料的有效热导率可以表示如下：

式中，keあ是复合材料的有效热导率，kp是填料的热导率，km是被填充材料的热导率，φ代表填充粒子的体积分数。随后Kapitza等人进一步改进了MGEMT，理论体系中考虑了填充粒子与被填充有机材料之间的界面热阻(Kapitza热阻)[19]对复合材料热导率的影响，是目前有效介质理论中与实验条件符合最好的理论体系。但是基于MGEMT的理论局限，填充粒子的体积分数必须限制在很小的范围内，这一点使得MGEMT无法拟合高填充体积分复合材料的热输运行为。

而在Bruggeman EMT中[20]，对于填充粒子的体积分数没有限制。对于一个以球形填充物随机填充的有机复合材料，利用Bruggeman EMT可以得到：

当填充粒子的体积分数φ足够小的时候，Bruggeman EMT得到的热导率结果与 MGEMT结果类似。但是Bruggeman EMT中并未将填充粒子与被填充材料的界面热阻考虑在内，这一点使得Bruggeman EMT并不能很好地拟合现有的实验数据。

以上理论只考虑填充粒子的形状与体积分数对复合材料热输运体系的影响，能够很好地描述当填充粒子尺寸足够大时（大于微米尺寸）复合材料的热输运行为。然而近年来在纳米流体（流体中填充纳米颗粒的复合材料）方向的研究表明，纳米流体的热导率相较于未填充流体的热导率有显著增大并且伴有明显的温度依赖效应[21−23]，这种纳米流体热导率的急剧增大趋势明显偏离了 MGEMT与Bruggeman EMT的预期结果。这一点表明当填充粒子的尺寸在纳米量级时，复合材料的热输运性质已无法通过 MGEMT与Bruggeman EMT进行描述[24]。

Keblinski与其合作者就上述问题提出了四种可能引发纳米流体热导率急剧增大的影响因素：填充颗粒的布朗运动、流体与填充颗粒界面的分子级分层、纳米颗粒的弹道输运机制以及填充颗粒团簇[25]。基于此猜想，Keblinski等人提出了由静止粒子模型与运动粒子模型组成的体系[26]。静止粒子模型假设在复合材料体系内存在两条并行的热传输通道，一条用于填充颗粒传热，另一条用于流体材料本身传热。那么纳米流体复合材料的有效热导率可以表示为：

此模型中将流体粒子与填充粒子都假设为球形颗粒，以rm与rp分别表示流体粒子与填充粒子的半径。而在运动粒子模型中，上式中kp是一个与填充粒子运动的平均速度（vp）有关的物理量，vp与粒子的布朗运动密切相关并且具有很强的温度依赖关系。因此静止粒子模型与运动粒子模型相结合能够解释纳米流体热导率的温度依赖关系。

Keblinski的理论建立在不考虑填充粒子与被填充材料之间接触热阻的假设之上，然而实际情况中将无机填料掺入有机载体的过程中势必会引入界面热阻，界面热阻已经成为有机复合材料热导率的一个重要组成部分[27,28]。Hasselman,Johnson[29]以及Benvensite[30]在MGEMT的基础上提出将界面热阻作为有机复合材料热导率理论的组成部分，随后Nan和他的合作者们预测了含随机分布填充颗粒的复合材料的有效热导率为[31]：

α=RKkm/a,a代表填充颗粒的半径，RKkm叫做Kapitza半径。

现阶段的有效介质理论体系多数建立在MGEMT的基础之上，充分考虑了填充粒子与被填充材料之间的界面热阻，使得理论结果与实验结果符合的很好。其缺陷在于填充粒子的体积分数被限制在很低的范围内，这使得高填充体积分数的复合材料热输运性质还不能利用有效介质理论进行分析和解释。

III.微纳米高分子聚合物材料的热导测量方法以及目前的研究进展

A.微纳米高分子聚合物材料的热导测量方法

1.悬空热桥法

悬空微桥法采用预加工的悬空MEMS(microelectromechanical system)器件作为加热热源与温度传感器，可用于测量单根有机/无机纳米线、纳米管及二维材料如石墨烯和氮化硼。这种悬空器件通常可以使用深紫外光刻或电子束曝光技术进行加工[32]，如图2a所示。加热器(Rh)与温度传感器(Rs)是两个悬空的铂电阻器，由12根悬空铂/氮化硅悬臂支撑，其中四根用于测量待测样品的电阻以及热电信号，另外8根分别用于表征加热器与温度传感器的电阻。

图2.a悬空MEMS器件结构示意图;b悬空微桥法热流流向示意图

若想要对待测样品进行热导测量，首先需要对加热器进行加热使得待测样品两端产生可控的温度梯度。实验中整个悬空器件放入真空恒温器中（真空度高于1×10−3Pa）。当环境温度稳定后，向加热器施加一个交流/直流混合电流，直流用于给加热器提供热量，交流用于监测加热器的电阻变化(ΔRh)从而得到加热器上的温度变化(ΔTh)。在加热器上产生的焦耳热一部分通过六根铂/氮化硅的悬臂直接导向环境中，另一部分焦耳热则通过待测样品导向温度传感器一侧使得传感器的温度随之升高。温度传感器上施加与加热器上相同的交流电流以表征其温度的变化 (ΔTs)。图2b是利用悬空热桥法测量待测样品热导率的热流流向示意图。

当整个系统达到热平衡之后，在加热器铂电阻丝与通入直流电流的两根铂/氮化硅悬臂上总共产生的焦耳热为Q，其中Q1的焦耳热直接导入衬底中，另外Q2的焦耳热参与到热传输过程中。在此假设加热器与温度传感器内部没有温差，因此根据热流流向示意图，整个悬空器件上的热流分布情况可以用如下公式表示：

其中，Th为达到热平衡后加热器上的温度；Ts为达到热平衡后温度传感器上的温度；Gs为待测样品的热导；Gb为六根铂/氮化硅悬臂的总热导。

在测量得到样品的热导值Gs之后，待测样品的热导率可以通过样品的尺寸得到：

其中，κ为待测样品的热导率；L为样品长度；S为样品截面积。

2.激光闪光法(Laser flash)

激光闪光法是由 Parker及其合作者提出并研发成功的[33]，用于测量块状样品的纵向热导率。该方法具有样品的制备要求低，测量周期短以及温度范围广等一系列优势。近年来，激光闪光法已逐渐成为一种成熟的材料热物性表征手段。该方法无法直接测量样品的热导率，而是根据材料的热导率与其热扩散系数(D)，比热容(Cp)[33]以及体积密度(ρ)之间的关系而间接得到样品热导率[34,35]：

目前已经有很多种方法可以用来测定材料的热扩散系数D[36]，其中Angstrom法是一种最普遍的测试热扩散系数的方法[37]。假设热源以正弦加热功率对待测样品的一端进行加热，待测样品的另一端保持环境温度。热量将以正弦的波动在样品两端之间扩散，一段时间之后在未加热的一端同样会受到正弦加热的影响而产生一个不同于加热端的相位。利用样品两端温度随时间的变化关系，能够通过以下公式得到待测样品的热扩散系数：

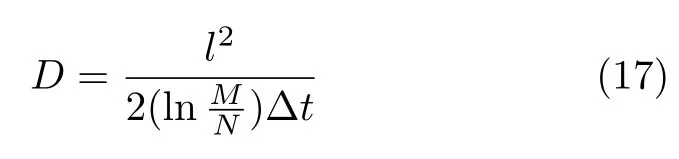
其中，l为待测样品长度；M为加热端温度的振幅；N为远离加热端温度的振幅；Δt是加热热量由加热端扩散至另一端所需的时间间隔。

待测样品的比热容Cp可以利用已知比热容的标样来进行表征，控制标样与待测样品以完全相同的加热功率进行加热，如此根据能量平衡方程可知：

其中，Cps为标样的比热容；ms与m分别为标样与待测样品的质量；ΔTs与ΔT分别为标样与待测样品以同样的加热功率加热时所能获得的最大温升。

3.3ω法

3ω法是一种较为简单的热导率测量方法。测量时，需在待测样品上制备一定大小与厚度的金属电极作为热源，通入频率为1ω的交流电流对样品进行加热。此时金属电极上会产生2ω的温度变化信号。当电极上的温度变化足够小时，金属电阻可以近似认为与温度成线性关系，因此，金属电极上的电阻会出现频率为2ω的波动。在2ω电阻变化与1ω交流电流的共同作用下会产生3ω的电压信号。根据3ω电压信号的频域反馈特性可以间接测得待测样品的热导率。3ω法测量热导率的应用非常广泛，一维纳米线，二维薄膜以及块材均可利用3ω法进行热导率的表征。由于有机高分子复合材料通常以二维薄膜的形式旋涂或生长于不同的基底之上，所以这里重点介绍3ω表征二维薄膜热导率的测量原理。

3ω法测量薄膜法向热导率时，首先要满足热穿透深度大于薄膜厚度而小于基底厚度，同时金属电极的宽度要远大于薄膜厚度，这样才可以认为热量全部沿法向向下传递 (如图3a所示)[38]。实验中可测得相同的加热功率下，基底上的温度变化为ΔTs，薄膜样品与基底共同引起的温度变化为ΔTtotal，从而得到薄膜样品引起的温差为ΔT=ΔTtotal−ΔTs，由此可得到薄膜样品的法向热导率为：

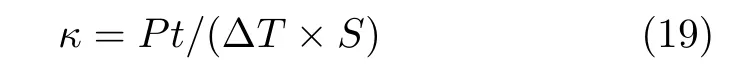
其中，P为加热功率；t为薄膜厚度；S为截面积；κ即为薄膜样品的法向热导率。

3ω法测量薄膜面内热导率的原理是建立在法向热导率测量之上的[39]，如图3b所示。在待测薄膜上同时制备两个不同宽度的金属电极，一个电极的宽度远大于待测薄膜厚度，另一个电极的宽度与薄膜厚度相近。根据上述法向热导率的测量原理分析可知，用宽电极对薄膜进行加热时热量是只沿法向传递的；而用窄电极加热时热量的传递是同时包括面内与法向两个方向的(如图3b所示)。因此可以通过法向与面内热量的传递关系计算获得待测薄膜的面内热导率：

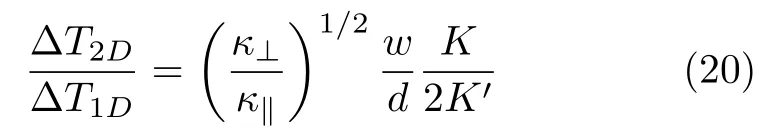
其中，ΔT1D是宽电极上的温度变化量；ΔT2D是窄电极上的温度变化量；w是窄电极的宽度；d是待测薄膜的厚度；κ⊥为薄膜的法向热导率；κ‖为薄膜的面内热导率；K与K′分别是第一类完全椭圆积分与互补的完全椭圆积分。

4.扫描热显微镜(SThM)

SThM（Scanning Thermal Microscope）作为一种高空间分辨率的探测样品表面热物理性质的系统，是在原子力显微镜 AFM基础上形成的。现在大多数 SThM是基于 AFM接触模式下的测量。如果将 AFM 的探针换成热扫描探针（热敏元件），并将探针接入电桥电路中，通过对探针电阻变化情况的测量，我们便可以探测热扫描探针的热量或者温度变化情况 (如图3c所示)。根据不同的直流或交流探测电流，SThM 可分为 DC-SThM 和 3ω-SThM[40−42]。目前 3ω-SThM 方法被用于纳米线的原位热导测量，例如2014年P3HT纳米线的热导率测量[43]。3ω-SThM法是给针尖电阻中通入交流电I(t)=I0sin(ωt)，会在针尖中产生频率为2ω热流PJoule和温度变化T2ω。在接触模式下，热量会从针尖流向样品表面，在针尖和样品间产生等效热阻Req。对于不同热导率的被扫描样品，这个热量变化不一样，故而针尖的温度变化也不同。对于热阻型的针尖，频率为2ω的温度变化会在针尖引起频率也为2ω的热阻变化。根据欧姆定律，针尖两端会产生频率为3ω的电压变化，并且这个电压变化和被扫描样品的热导率有关。3ω倍频的电压信号表达式为：

其中，Kampli是用lock-in测得的3ω信号，αtip是针尖的热扩散系数。根据V3ω信号的变化就可以反推出被扫描样品的热导率。

对于3ω-SThM方法，其测量的热流模型是点热源和样品接触，交流加热使热流在样品中具有一定的穿透深度，热量在样品中呈半球形扩散，近似各个方向传热相同。所以该方法适用于测量各向同性样品的热导率。

B.高分子聚合物纳米纤维的高热导率研究

有机高分子聚合物一直被认为是一种热绝缘材料，其块材或薄膜热导率都在 0.1 Wm−1K−1至0.3Wm−1K−1范围内[15,45,46]。2014年Kim与其合作者通过使PAP与其他有机高分子结合形成氢键的方法在一定程度上提高了高分子聚合物的热导率[46]。除

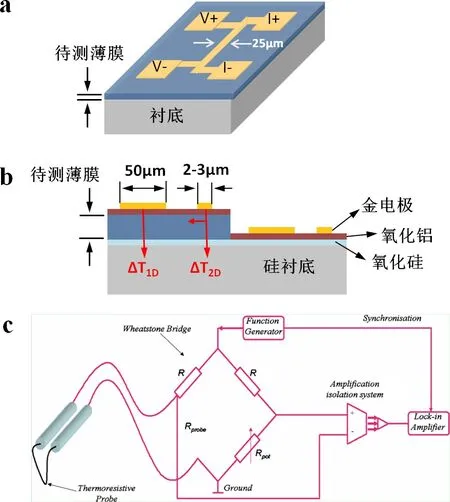
图3.a 3ω法测量薄膜法向热导率原理图 [38]；b 3ω法测量薄膜面内热导率原理图 [39]；c SThM 测量薄膜热导率原理图[44]。

此之外，近些年来一些研究结果表明单原子链的聚乙烯 (PE)能够实现非常高的热导率[15,45,46]。1999年，C.L.Choy对三种状态下的 PE(熔融状态的、胶体、单晶mat PE)进行了力学及热导率的测量。他发现随着拉伸比增大，PE轴向方向的热导率增加极快并达到 40Wm−1K−1，而纵向方向的热导率却有轻微的下降趋势。此现象极可能是在拉伸过程中，杨氏模量变化导致了热导率的变化[47]。

2010年，Gang课题组首次阐述了PE纳米纤维热导率的研究，最先拉开了有机纤维热导率研究的新篇章[48]。有机高分子块材中的分子链纠缠、杂质以及缺陷会对声子的传输过程起到阻碍作用。然而随着纳米纤维直径的减小，一部分纠缠在一起的分子链会沿着外力方向有序排列，由此可猜想声子在纳米纤维中受到的散射会远小于在块材中的情况[49−51]。1990年 Poulaert[52]以及 1998年Hiroyuki[53]的工作充分证明了上述猜想。利用这一想法 Gang课题组成功将PE拉成纳米纤维从而得到104Wm−1K−1的极高热导率[48](如图4所示)。

随着这一突破性进展的问世，对于有机纳米纤维热输运的研究也受到越来越多的关注。2011年，Bing利用自己生长的 PE纳米纤维，比较了 PE纳米纤维阵列及单根纳米纤维的热导率,结果证明单根纳米纤维的热导率 (36.5Wm−1K−1)高于纳米阵列的热导率 (21.1Wm−1K−1)[54]。2013年，Cahill,D.G.发现 PE晶体以及 PE液晶的热导率可高达 20Wm−1K−1。同时，他们发现了 PE纳米纤维在高温区都满足由声子-声子散射引起的κ～ 1/T关系[55]。

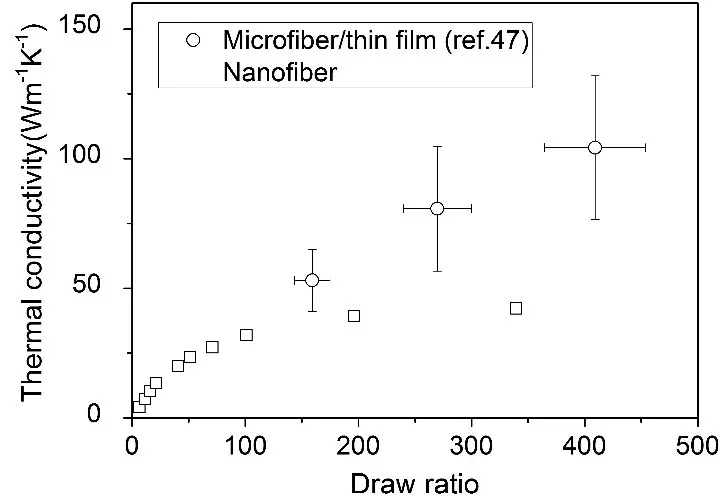
图4.PE纤维的热导率随着拉伸比增大而显著增大[48]

继 PE纳米纤维高热导率被发现之后，2014年，Renkun Chen课题组对另外一种常见有机物 Nylon-11纤维热导率进行了表征[56]。他们将 Nylon-11溶液利用静电纺丝的方法拉成直径不等的纤维。静电纺丝技术从 20世纪 90年代开始受到广泛关注，特别是近年来，随着有机高分子纳米技术的发展，静电纺丝技术成为集成化、大规模生产有机高分子纳米纤维的一种有效手段[57−62]。 Renkun Chen课题组沿用热电桥法[63−69]表征了直径为 73nm 的 Nylon-11纤维在室温下热导率为 1.6Wm−1K−1,是 Nylon-11块材热导率的20倍。同时实验结果指出高分子有机物的结晶度是其纳米纤维能否获得高热导率的一个重要因素：高结晶度有机材料制备成的纳米纤维能够获得更高热导率。同年，Li的课题组介绍了无定形聚噻吩(polythiophene)的热性质。他们得出了随着纳米纤维直径的减小，热导率增加非常明显。他们所测得的最高的热导率达到了4.4Wm−1K−1，是块材聚噻吩热导率的23倍[15]。在这一工作中Li及其合作者首次尝试用MTCM[70]解释聚噻吩热导率随温度变化的行为。由于最小热导率模型采用bulk polymer的声速进行模拟，所以导致模拟值与实验值之间存在偏离[8]。

此后，2017年Wen与其合作者对一种常见的有机热电纳米纤维(PEDOT)进行了热性质表征[71]。实验中他们利用非平衡态分子动力学模拟 (NEMD)设计了两种不同分子量的 PEDOT纳米纤维，结果显示 PEDOT纳米纤维的结晶度与其热导率之间有很强的依赖关系。对于相对分子量为5600的纳米纤维，随着纳米纤维结晶度由 0.49提高到0.87，其热导率由 0.97Wm−1K−1增大至 4.88Wm−1K−1；而对于相对分子量为14000的纳米纤维，随着纳米纤维结晶度由0.54提高到0.89，其热导率由1.67Wm−1K−1激增至6.66Wm−1K−1。这一结果有力地证实了高结晶度的有机纳米纤维材料能够获得更高的热导率。

综上所述，虽然有机高分子聚合物材料的合成与应用取得了突破性进展，但是关于低维有机高分子聚合物热输运调控的研究依旧甚少。有机高分子聚合物热传输的方式不同于传统晶体材料，它主要是依靠聚合物内部分子链内与链间的分子相互作用来传递能量。高分子聚合物内部的分子链互相交叠嵌套，空间结构极其复杂，这一点使得现存的热传输理论模型已无法解释聚合物的热传输行为，因此目前亟待大量的实验研究结果支撑并建立新的理论模型以阐述高分子聚合物材料的热传输本质。同时，需进一步深入探索低维高分子聚合物热导率的温度依赖关系与尺寸效应。

C.自组装有机高分子链 (SAMs)对界面热导的调控

界面热导材料在使用过程中需经历多次升降温，剧烈的温度变化使得界面热导材料加速老化并最终导致脱胶（即图1c中Rint无穷大）。一个可行的办法是利用自组装有机高分子链，利用链末端的基团（例如：-H，-Cl，-SH等）与基底材料强结合从而降低热阻，并减缓老化。高分子链末端的不同基团分子能够与基底分子之间产生相互作用，相互作用的强弱直接制约了有机高分子链与基底之间的界面热导的强弱。

2012年，Losego及其合作者表征了石英-SAMs-金多层结构的界面热导性质[72]，实验中利用 CH3-基与 SH-基高分子链调控界面上的热输运性质。结果表明CH3-基高分子与金原子之间仅有很弱的范德华力结合作用，所测界面热导相当低，而 SH-基与金原子之间存在较强的共价键结合作用，这种强的共价键结合使得 SH-基多层结构的界面热导高达 65MWm−2K−1。同时他们还表征了当界面上共价键的数量逐渐增加时，多层结构的界面热导表现出了显著的增大趋势（见图5）。

2016年，Zheng与其合作者在研究SAMs对于界面热导的调控时，发现界面热导的大小除了与界面处的分子结合力相关之外，还与界面上分子的溶度参数有关[73]。实验中使用了蓝宝石 -SAMs-PS的多层结构，并发现-Cl与PS具有极为接近的溶度参数，这一点使得-Cl基能够更好的与PS分子结合从而增大界面处的界面热导。

图5.界面热导随界面上共价键比例的增大而增大[72]

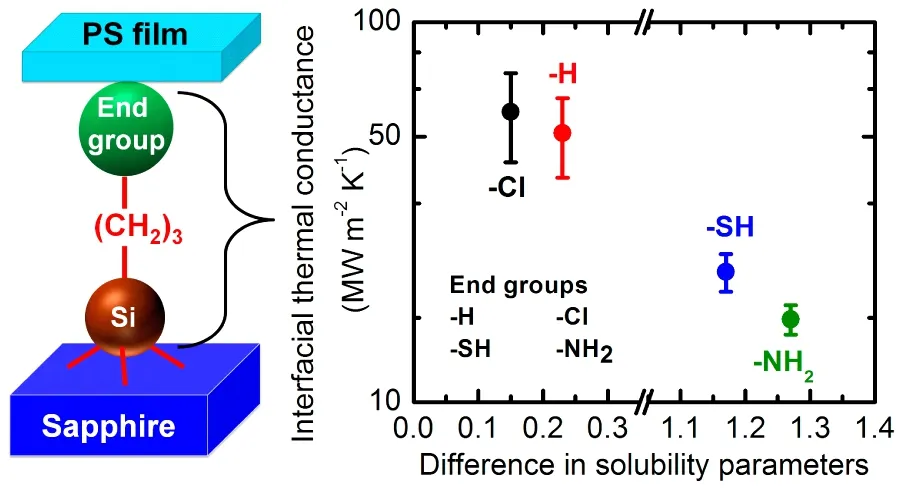
图6.界面热导与溶度系数之间的依赖关系[73]

D.有机纳米复合材料的热输运调控

1.碳基复合材料

聚合物基复合材料目前以碳基（碳纳米管CNT[74,75]、石墨 graphite[76,77]、石墨烯 graphene[78−80]等）复合材料研究居多，被填充的基材料包括环氧树脂 (epoxy)[81−83]、聚苯乙烯[23,84,85]、聚乙烯醇 (PVA)[79,86−88]、聚 苯 胺 (PANI)[89−92]、聚氨酯(PU)[93,94]、PMMA[95−100]、尼龙[101]、 UltemTM[102]等一系列有机高分子聚合物。

Cai和他的合作者将多壁碳纳米管(MWCNTs)分散掺入聚氨酯(PU)中以提高复合材料的热导率[103]。实验中他们通过改变十二烷基硫酸钠(SDS)与MWCNTs的重量比来控制 MWCNTs在聚氨酯中的分散程度[104]：当 SDS与 MWCNTs的重量比小于 1:3时，MWCNTs无法继续在 PU中分散；而当 SDS与 MWCNTs的重量比为 1:1时，复合材料热导率在MWCNTs含量为3wt%时出现下降趋势，这是由于高分子基材料结构中留给填料的空间是很有限的，当 MWCNTs含量超过 3wt%时，MWCNTs出现堆簇的行为直接导致了纳米管管壁之间声子散射增加使得复合材料的热导率下降。即使是用SDS促进纳米管的分散，MWCNT/PU复合材料的热导率最高也只达到0.47Wm−1K−1,这对于解决实际的散热问题是远远不够的。

图7.MWCNT/PU复合材料的热导率随碳纳米管的重量百分比的变化关系[103]

近些年来有机纳米复合材料热传输研究的重心逐渐转移至以石墨烯为填料的复合材料。原因主要是由于单层石墨烯的面内热导率高达 3000—5300Wm−1K−1[84,105,106]，用高热导率的纳米材料作为填料有望使得有机复合材料的热导率进一步提高。

Teng和合作者们利用不同的纳米填料填充环氧树脂形成有机纳米复合材料[107]，并且比较了MWCNTs/epoxy、Graphene/epoxy、Py-PGMA-graphene/epoxy、Exfoliatedgraphite(机械剥离石墨烯)/epoxy[83]四种有机复合材料热导率随填充量改变的变化情况。图8表示的是石墨烯薄片的功能化过程，Py-PGMA基团进入石墨薄片之间并与碳原子之间形成共价键 Py-PGMA-graphene[108]。这种 Py-PGMA-graphene填料能够与环氧树脂分子形成共价键结合，从而减小石墨烯薄片与环氧树脂之间的界面热阻而使得热传输更容易实现。这使得所测 Py-PGMA-graphene/epoxy热导率可达到 1.9Wm−1K−1。

表一中较为详尽的总结了近年来碳基有机复合材料热输运方向的研究成果，结果显示对有机材料进行碳材料的填充确实是一种提高复合材料热导率的有效手段。

图8.石墨烯薄片的功能化过程以及 Py-PGMA-graphene/epoxy复合材料的热导率[107]

2.金属基复合材料

金属填料包括粉末、薄片以及纳米线，常用到的材料有铝、铜、铁、银、金和镍等[109,110]。2013年 Balachander和合作者们制备了金纳米线/PDMS复合材料，发现在金纳米线填充体积为 3vol%时热导率达到 5.0Wm−1K−1[111]。Xu等人发现 9vol%银纳米线阵列与聚碳酸酯的复合材料热导率可达到 30.3Wm−1K−1[112]。Zhu等人比较了不同长径比的铜纳米线作为填料时，整体复合材料热导率的变化，结果显示较大长径比的铜纳米线在基材料内更容易建立热输运通道，从而得到较高的热导率[113]。金属填料虽然没有碳基材料那么高的自身热导率，但是实验证明金属填料能够有效的减小复合材料内部的界面热阻，这一点使得金属有机复合材料逐渐受到重视。但金属有机复合材料本身具有缺陷：a)金属填料会使得复合材料柔性下降易断裂；b)金属有机复合材料的高电导决定了其无法作为绝缘散热器件加以应用。

3.其他填料的有机复合材料

氧化铝 (Al2O3)[114]、氮化铝 (AlN)[115]、氮化硼 (BN)[116,117]、碳化硅 (SiC)[118]等陶瓷材料因其高热导率、高电阻率以及优良的热稳定性同样被广泛用做有机复合材料的填充剂。Ishida在实验中获得热导率高达32.5Wm−1K−1的BN/polybenzoxazine有机复合材料[119]。该复合材料的高热导率很大程度上得益于 BN的高热导率。相较于BN作为填料的复合材料，以 SiN为填料的有机复合材料热导率会低很多。2006年 Hong He与其合作者制备了Si3N4/polystyrene[120]复合材料，该复合材料的热导率最优值仅有 3.0Wm−1K−1[120]。由实验结果总结可知，高热导率的纳米填料是调控有机复合材料热传输性质的一个关键因素，也是今后优化有机复合材料热传输性质的努力方向。

IV.高分子聚合物热输运调控的展望

综上所述，在材料科学与工程应用领域，聚合物基热界面材料已经有着广阔的实用案例和应用前景，有机高分子材料的合成与应用已取得较好的进展，高分子聚合物（薄膜、纳米纤维）的制备技术已趋于成熟。然而其内在热传输机理仍不清楚，对其研究仍处于起步阶段。目前面临的问题和挑战主要有：

1.关于低维有机高分子聚合物（薄膜、纳米纤维）热输运调控的实验研究甚少，使得高分子热传输理论模型缺少实验的支撑。有机高分子聚合物内部分子链互相交叠嵌套，使得热传输机制变得极为复杂。所以亟待大量的实验结果用以建立新的理论模型，以阐述高分子聚合物材料的热传输本质。

2.有机高分子热导率的测量依旧存在瓶颈。虽然近年来激光闪光法以及3ω法被广泛应用于测量高分子有机材料的热导率，但是该方法均基于一定的理论模型或假设，不可避免会引入很大的测量误差。

3.目前用于商业用途的聚合物基热界面材料热导率基本在 2 Wm−1K−1至 8Wm−1K−1之间，尚不足以解决半导体核心器件的散热问题。要彻底解决器件散热问题，则需要研制出热导率在 20Wm−1K−1以上，界面总热阻低于 0.01 Kcm2/W的热界面材料。

表I.常见的碳基有机复合材料热导率

4.本文提到通常采用在聚合物中添加高热导率填料用于降低总界面热阻。然而，更重要的是，目前还没有很好的方法能够降低聚合物基热界面材料与其它材料如封装外壳或金属散热片之间的界面热阻。近年来，美国数个课题组在DARPA的支持下尝试了多种方法，如纳米金属弹簧、柔性石墨膜或纳米碳管等[121]。虽然实验已取得一定进展，但是离实际应用还有相当长的一段距离。

鉴于以上困难与瓶颈，现阶段在基础研究领域对于有机高分子热输运的研究重点可以从三个方面着手：

1.声子 hopping机制的理论与热渗流理论的发展[122]。

2.自组装高分子结构的界面热导研究与调控（范德华力结合、共价键结合、离子键结合）。

3.有机高分子链的有序度对其热输运性质的影响。

同时，对聚合物材料热传导机制的研究可为有机热电提供理论指导。我们都知道热电材料的品质因子，是由 seebeck系数 S，电导率σ和热导率κ相互制约共同决定的。所以有效调控材料的热输运，使得材料电导率维持的条件下尽可能的降低其热导率就成为热电材料获得高品质因子的必要途径。

致谢

国家重点研发计划“战略性先进电子材料”重点专项（项目编号：2017YFB0406000）；自然科学基金面上项目（项目编号：11674245）；上海市科学技术委员会科研计划项目（项目编号：17ZR1447900和17142202100）；中央高校基本科研业务费专项资金。

[1]Franklin A D.Science,2015,349:2750

[2]Moore A L,Shi L.Mater.Today,2014,17:163

[3]Waldrop M M.Nature,2016,530:144

[4]Liu S,Xu X,Xie R,et al.Eur.Phys.J.B,2012,85:1

[5]Yang N,Xu X,Zhang G,et al.AIP Adv.,2012,2:041410

[6]徐象繁,杨诺,李保文.物理,2013,42:181

[7]周俊,李保文.物理,2013,42:89

[8]Cahill D G,Watson S K,Pohl R O.Phys.Rev.B,1992,46:6131

[9]Einstein A.Ann.Phys.,1907,22:180

[10]Einstein A.Ann.Phys.,1911,340:679

[11]Allen P B,Feldman J L.Phys.Rev.B,1993,48:12581

[12]Allen P B,Feldman J L,Fabian J,et al.Philos.Mag.B,1999,79:1715

[13]Hsieh W P,Losego M D,Braun P V,et al.Phys.Rev.B,2011,83:174205

[14]Kim G H,Lee D,Shanker A,et al.Nat.Mater.,2015,14:295

[15]Singh V,Bougher T L,Weathers A,et al.Nat.Nanotech.,2014,9:384

[16]Alexander S,Entin-Wohlman O,Orbach R.Phys.Rev.B,1986,34:2726

[17]Garnett J M.Philos.Trans.R.Soc.London,Ser.A,1904,203:805

[18]Hamilton R,Crosser O.I&EC Fundamentals,1962,1:187

[19]Kapitza P.Phys.Rev.,1941,60:354

[20]Bruggeman D.Ann.Phys.(Leipzig),1935,24:636

[21]Patel H E,Das S K,Sundararajan T,et al.Appl.Phys.Lett.,2003,83:2931

[22]Choi S,Zhang Z,Yu W,et al.Appl.Phys.Lett.,2001,79:2252

[23]Eastman J A,Choi S,Li S,et al.Appl.Phys.Lett.,2001,78:718

[24]Keblinski P,Eastman J A,Cahill D G.Mater.Today,2005,8:36

[25]Keblinski P,Phillpot S,Choi S,et al.Int.J.Heat Mass Trans.,2002,45:855

[26]Kumar D H,Patel H E,Kumar V R,et al.Phys.Rev.Lett.,2004,93:144301

[27]Li Q,Guo Y,Li W,et al.Chem.Mater.,2014,26:4459

[28]Hu L,Desai T,Keblinski P.Phys.Rev.B,2011,83:195423

[29]Hasselman D,Johnson L F.J.Compos.Mater.,1987,21:508

[30]Benveniste Y.J.Appl.Phys.,1987,61:2840

[31]Nan C W,Birringer R,Clarke D R,et al.J.Appl.Phys.,1997,81:6692

[32]段文晖,张刚.纳米材料热传导.科学出版社，2017

[33]Parker W,Jenkins R,Butler C,et al.,J.Appl.Phys.,1961,32:1679

[34]Baba T,Ono A.Meas.Sci.Technol.,2001,12:2046

[35]Weidenfeller B,H¨ofer M,Schilling F R.Composites Part A,2004,35:423

[36]Dos Santos W N.Polym.Test.,2005,24:932

[37]Lopez-Baeza E,De La Rubia J,Goldsmid H.J.Phys.D,1987,20:1156

[38]Cahill D G,Katiyar M,Abelson J.Phys.Rev.B,1994,50:6077

[39]Kim G,Shao L,Zhang K,et al.Nat.Mater.,2013,12:719

[40]Majumdar A.Annu.Rev.Mater.Sci.,1999,29:505

[41]Shi L,Majumdar A.J.Heat Trans.,2002,124:329

[42]Lef`evre S,Volz S.Rev.Sci.Instrum.,2005,76:033701

[43]Rojo M M.Mart´ın J,Grauby S,et al.Nanoscale,2014,6:7858

[44]Puyoo E,Grauby S,Rampnoux J M,et al.,J.Appl.Phys.,2011,109:024302

[45]Springer H L.Introduction to Physical Polymer Science.Wiley-Interscience,2006

[46]Kim G H,Lee D,Shanker A,et al.Nat.Mater.,2015,14:295

[47]Choy C,Wong Y,Yang G,et al.J.Polym.Sci.B,1999,37:3359

[48]Shen S,Henry A,Tong J,et al.Nat.Nanotech.,2010,5:251

[49]Chae H G,Kumar S.Science,2008,319:908

[50]Smith P,Lemstra P J.J.Mater.Sci.,1980,15:505

[51]Choy C,Fei Y,Xi T.J.Polym.Sci.B,1993,31:365

[52]Poulaert B,Chielens J C,Vandenhende C,et al.Polym.Commun.,1990,31:148

[53]Fujishiro H,Ikebe M,Kashima T,et al.Jpn.J.Appl.Phys.,1998,37:1994

[54]Cao B Y,Li Y W,Kong J,et al.Polymer,2011,52:1711

[55]Wang X J,Ho V,Segalman R A,et al.Macromolecules,2013,46:4937

[56]Zhong Z,Wingert M C,Strzalka J,et al.Nanoscale,2014,6:8283

[57]Rein D M,Cohen Y,Lipp J,et al.Macromol.Mater.Eng.,2010,295:1003

[58]Ren G,Cai F,Li B,et al.Macromol.Mater.Eng.,2013,298:541

[59]Gheibi A,Bagherzadeh R,Merati A A,et al.J.Polym.Res.,2014,21:1

[60]Weber N,Lee Y S,Shanmugasundaram S,et al.Acta Biomater.,2010,6:3550

[61]Mandal D,Yoon S,Kim K J.Macromol.Rapid Commun.,2011,32:831

[62]Lee S W,Lee H J,Choi J H,et al.Nano Lett.,2009,10:347

[63]Kim P,Shi L,Majumdar A,et al.Phys.Rev.Lett.,2001,87:215502

[64]Xu X,Pereira L F,Wang Y,et al.Nat.Commun.,2014,5:3689

[65]Wingert M C,Chen Z C,Kwon S,et al.Rev.Sci.Instrum.,2012,83:024901

[66]Shi L,Li D,Yu C,et al.J.Heat Trans.,2003,125:881

[67]Chen R,Hochbaum A I,Murphy P,et al.Phys.Rev.Lett.,2008,101:105501

[68]Wang C,Guo J,Dong L,et al.Sci.Rep.,2016,6:25334

[69]Xu X,Chen J,Li B.J.Phys.:Condens.Matter,2016,28:483001

[70]Osinin S,Nosov M.Mech.Compos.Mater.,1966,2:4

[71]Shi W,Shuai Z,Wang D.Adv.Func.Mater.,2017,27:1702847

[72]Losego M D,Grady M E,Sottos N R,et al.Nat.Mater.,2012,11:502

[73]Zheng K,Sun F,Zhu J,et al.ACS nano,2016,10:7792

[74]Gojny F H,Wichmann M H,Fiedler B,et al.Polymer,2006,47:2036

[75]Haggenmueller R,Guthy C,Lukes J R,et al.Macromolecules.2007,40:2417

[76]Min C,Yu D,Cao J,et al.Carbon,2013,55:116

[77]Hung M T,Choi O,Ju Y S,et al.Appl.Phys.Lett.,2006,89:023117

[78]Fang M,Wang K,Lu H,et al.J.Mater.Chem.,2009,19:7098

[79]Ramanathan T,Abdala A,Stankovich S,et al.Nat.Nanotech.,2008,3:327

[80]Vadukumpully S,Paul J,Mahanta N,et al.Carbon,2011,49:198

[81]Yu A,Ramesh P,Itkis M E,et al.J.Phys.Chem.C,2007,111:7565

[82]Yu A,Ramesh P,Sun X,et al.Adv.Mater.,2008,20:4740

[83]Ganguli S,Roy A K,Anderson D P.Carbon,2008,46:806

[84]Stankovich S,Dikin D A,Dommett G H,et al.Nature,2006,442:282

[85]Tu H,Ye L.Polym.Adv.Technol.,2009,20:21

[86]Lee Y R,Raghu A V,Jeong H M,et al.Macromol.Chem.Phys.,2009,210:1247

[87]Liang J,Huang Y,Zhang L,et al.Adv.Func.Mater.,2009,19:2297

[88]Yu J,Lu K,Sourty E,et al.Carbon,2007,45:2897

[89]Peponi L,Tercjak A,Verdejo R,et al.J.Phys.Chem.C,2009,113:17973

[90]Wang D W,Li F,Zhao J,et al.ACS nano,2009,3:1745

[91]Zhao L,Zhao L,Xu Y,et al.Electrochim.Acta,2009,55:491

[92]Yan J,Wei T,Fan Z,et al.J.Power Sources,2010,195:3041

[93]Kim H,Miura Y,Macosko C W.Chem.Mater.,2010,22:3441

[94]Liang J,Xu Y,Huang Y,et al.J.Phys.Chem.C,2009,113:9921

[95]Chen G,Wu D,Weng W,et al.Carbon,2003,41:619

[96]Chen G,Weng W,Wu D,et al.Eur.Polym.J.,2003,39:2329

[97]Zheng W,Wong S C.Compos.Sci.Technol.,2003,63:225

[98]Zheng W,Wong S C,Sue H J.Polymer,2002,43:6767

[99]Yuen S M,Ma C C M,Chiang C L,et al.Composites Part A,2007,38:2527

[100]Guthy C,Du F,Brand S,et al.J.Heat Trans.,2007,129:1096

[101]Fukushima H,Drzal L,Rook B,et al.J.Therm.Anal.Cal.,2006,85:235

[102]Ghose S,Working D C,Connell J W,et al.High Perform.Polym.,2006,18:961

[103]Cai D,Song M.Carbon,2008,46:2107

[104]Jiang L,Gao L,Sun J.J.Colloid Interface Sci.,2003,260:89

[105]Balandin A A,Ghosh S,Bao W,et al.Nano Lett.,2008,8:902

[106]Ghosh S,Calizo I,Teweldebrhan D,et al.Appl.Phys.Lett.,2008,92:151911

[107]Teng C C,Ma C C M,Lu C H,et al.Carbon,2011,49:5107

[108]McAllister M J,Li J L,Adamson D H,et al.Chem.Mater.,2007,19:4396

[109]Sato K,Ijuin A,Hotta Y.Ceram.Int.,2015,41:10314

[110]Zhou W,Yu D.J.Appl.Polym.Sci.,2010,118:3156

[111]Balachander N,Seshadri I,Mehta R J,et al.Appl.Phys.Lett.,2013,102:093117

[112]Xu J,Munari A,Dalton E,et al.J.Appl.Phys.,2009,106:124310

[113]Zhu D,Yu W,Du H,et al.J.Nanomater.,2016,2016:8

[114]Sim L C,Ramanan S,Ismail H,et al.Themochim.Acta,2005,430:155

[115]Choi S,Kim J.Composites B,2013,51:140

[116]Gu J,Liang C,Dang J,et al.RSC Adv.,2016,6:35809

[117]Kim K,Kim M,Hwang Y,et al.Ceram.Int.,2014,40:2047

[118]Yu W,Wang M,Xie H,et al.Appl.Therm.Eng.,2016,94:350

[119]Ishida H,Rimdusit S.Themochim.Acta,1998,320:177

[120]He H,Fu R,Shen Y,et al.Compos.Sci.Technol.,2007,67:2493

[121]Bar-Cohen A,Matin K,Narumanchi S.J.Electron.Packag.,2015,137:040803

[122]Dong L,Xi Q,Chen D,et al.Nat.Sci.Rev.,2018,DOI:10.1093/nsr/nwy004