基于Morlet小波变异的粒子群优化算法
2018-04-16张超
张超
(宿州职业技术学院计算机信息系,安徽 宿州 234101)
0 引言
粒子群优化算法(particle swarm optimization,PSO)是KENNEDY和EBERHART[1]在1995年受鸟群觅食行为启发而仿生设计的群体智能全局优化算法。SHI和EBERHART[2]在1998年将惯性权重加入到PSO中,并提出线性递减的惯性权重(linear decreasing inertia weight,LDIW)思想,以平衡算法的全局搜索和局部搜索,一般将其默认为标准粒子群算法(standard PSO,SPSO)。SPSO算法因设计简单、易于实现,已被广泛应用于众多工程和科学领域[3-6]。但SPSO算法易陷入局部极值导致算法“早熟”,在处理高维优化问题时表现更为明显,收敛精度不高。为此,许多学者对SPSO进行了优化和改进,产生了一些比较著名的改进算法:FIPS[7]、CLPSO[8]、APSO[9]等。SPSO的改进工作主要可归纳为4个方面:①从SPSO算法自身参数,如惯性权重、学习因子等入手进行优化[10-11];②将其他智能算法思想融入到SPSO中的混合SPSO算法[12-13];③使用分布函数,如高斯分布[14]、t-分布[15]、小波函数等对粒子位置或粒子速度的更新方式进行扰动,帮助粒子跳出局部极值;④将其他学习策略,如混沌搜索[16]、反向学习[17]等引入SPSO算法中,加大算法的搜索空间,提高算法获得最优值的概率。由于SPSO算法本身没有跳出局部极值的机制,所以从①和②两个方面对算法进行优化,无法根本解决SPSO算法的“早熟”问题。从③和④两个方面入手的改进策略增加了算法跳出局部极值的机制,一定程度上弥补了SPSO算法的缺陷。
文献[18]提出一种小波变异的粒子群算法(hybrid particle swarm optimization with wavelet mutation,HPSOWM)。文献[19]将此种小波函数变异方式应用到二进制粒子群算法中。文献[20]对HPSOWM算法的变异形式进行了改进。文献[21-22]均使用Morlet小波函数采用不同的变异策略对粒子群算法进行了改进。文献[18-22]都指出小波变异能够对粒子起到微调作用,促使粒子偏离当前位置扩展到更大搜索区间,帮助粒子跳出局部极值。这些研究中所使用的变异策略虽提升了算法的性能,但算法整体收敛精度不高,还有待提升。
鉴于此,本文使用文献[18]提出的带尺度参数的小波函数对粒子进行变异操作,并提出一种基于Morlet小波变异的粒子群优化算法(particle swarm optimization algorithm based on Morlet wavelet mutation, MPSO)。MPSO算法以一定概率对每代全局最优粒子的各维度进行扰动变异操作,将变异结果作为当前粒子进行位置更新的新位置。此策略既充分利用了全局最优粒子所包含的优势信息,引导其他粒子快速朝着最优位置靠近,提高收敛速度;同时通过小波变异操作的微调作用在最优解周围扩展搜索空间,增大获得全局最优解的概率。
1 标准粒子群优化算法
SPSO算法粒子使用速度、位置和适应度值表示粒子的特征,每个粒子通过跟踪个体极值和全局极值不断更新飞行速度和位置,到达新的位置后使用适应度值评价粒子的优劣。其数学描述如下:
假设在D维搜索空间,存在由n个粒子组成的种群X=(X1,X2,…,Xn),第i个粒子在搜索空间中的位置可表示为,其速度为,通过适应度函数可计算第i个粒子的个体极值Pi=(pi1,pi2,…,pij,…,pid),全局极值Po为Pi中最优的,Po=每个粒子通过(1)式和(2)式更新速度和位置。
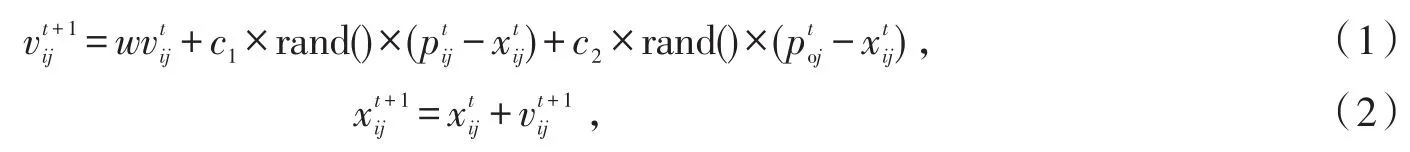
其中c1、c2为学习因子,一般取值为2;w为惯性权重,使用(3)式计算,其值从wmax到wmin线性递减。

其中t为当前迭代次数,T为最大迭代次数。
2 小波变异的粒子群优化算法
2.1 HPSOWM算法变异策略
HPSOWM算法[18]中每个粒子都有变异机会,变异由用户定义的变异参数pm∈[0,1]控制,对于每个粒子,如果随机产生一个随机数小于等于pm,那么该粒子将被选择发生变异。假设为第p代被选择的粒子,为该粒子第j维,为第j维搜索边界。按(4)式进行变异,


其中ψ(x)为小波函数,a为尺度参数,选择Morlet小波作为小波基,其具体形式如下:

这样,(5)式小波函数值σ的计算可表示为

小波函数超过99%的能量包含在[-2.5,2.5]之间,所以(7)式中j的取值范围为之间的伪随机数。尺度参数a的计算公式为

其中t为当前迭代次数,T为最大迭代次数,g为a的上限,ζwm为单调递增函数的形状参数。
2.2 MPSO算法变异策略
相较高斯分布、柯西分布、t-分布,Morlet小波产生正数和负数的概率是相同的,因此在局部空间搜索更为频繁,更容易获得最优解。为此,本文对HPSOWM算法变异策略进行改进,当某代粒子被选择进行变异时,使用(7)式的小波函数对组成当代最优粒子的各维度进行随机扰动,将扰动结果作为被选中变异粒子的新位置。计算公式如下:

算法1 MPSO算法执行流程

3 实验与结果分析
3.1 实验方案设计和部署
分别从固定迭代次数下的收敛精度、固定精度下的收敛速度和时间复杂度3个方面,比较MPSO算法与SPSO算法、HPSOWM算法、CLPSO算法及DEOPSO[17]算法的性能。性能分析实验在12个经典测试函数上进行,函数的名称、表达式、变量范围、理论极值和目标精度设定见表1。实验部署在主频2.50 GHz的CPU,4 GB内存,64位Win10操作系统的计算机上,使用MATLAB R2012a编程实现仿真程序。

表1 经典测试函数Tab.1 Classical test functions
为防止因为偶然性带来的误差,仿真程序分别连续独立运行50次。算法参数设置:5种算法的种群规模、最大迭代次数及函数维度都设定为n=30,T=1 000,d=30。CLPSO、DEOPSO、HPSOWM三种算法的学习因子和最大速度两个参数使用参考文献[8]和[17-18]的设定。MPSO和SPSO的学习因子c1=c2=2;在函数f10上Vmin=-0.2,Vmax=1,在其他函数上最大速度设定为搜索空间的一半。MPSO算法中g使用文献[18]推荐的取值g=20 000,单调递增函数的形状参数ζwm=5。
3.2 实验结果分析与比较
3.2.1 固定迭代次数下的收敛精度比较 算法性能评价使用最差值、最优值、优化平均值、标准差4个常用指标。表2为MPSO、SPSO、CLPSO、DEOPSO、HPSOWM五种算法在表1中6个高维单峰函数上的寻优结果。由表2可知,MPSO算法在5个函数(f1、f2、f3、f4、f6)上优化平均值排名第一,在这5个函数上最差值、最优值及50次实验的优化平均值均为函数的理论极值0,50次实验结果的标准差也为0,说明MPSO算法每次均能收敛到函数的理论极值,未陷入局部最优。MPSO算法在函数f5上的寻优结果不如HPSOWM,但高于SPSO、CLPSO和DEOPSO算法,并且HPSOWM算法在其他5个函数上的寻优结果大幅低于MPSO算法。
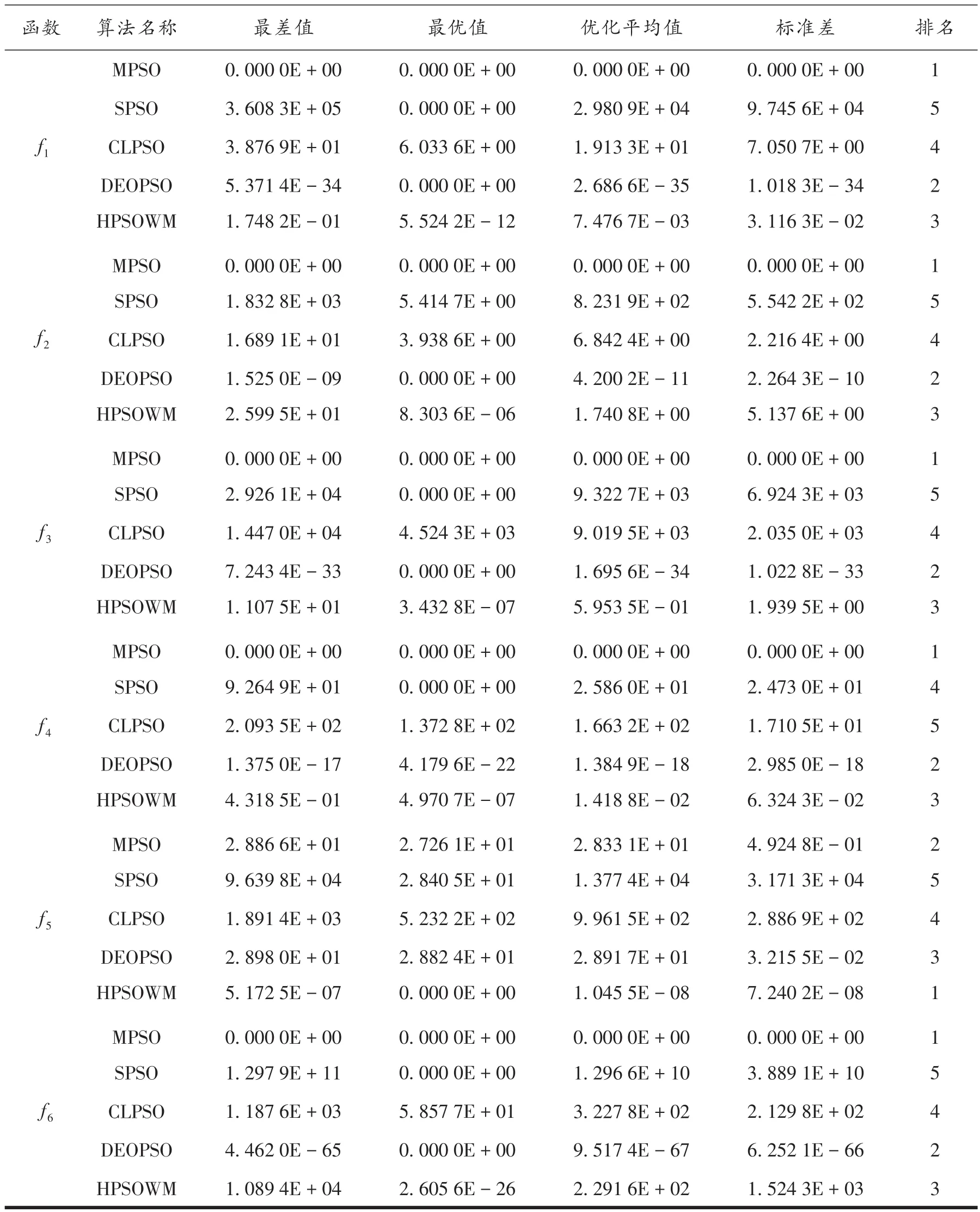
表2 高维单峰函数实验结果Tab.2 Experimental results of high-dimensional unimodal functions
表3为5种算法在表1中6个高维多峰函数上的寻优结果。由表3可知,MPSO在f7、f9、f11、f12四个函数上的最差值、最优值、优化平均值及标准差均为0,说明50次实验每次均能收敛到函数的理论极值。在函数f8上,MPSO算法与DEOPSO、HPSOWM算法的寻优能力相当。在函数f10上,MPSO算法的寻优精度略低于HPSOWM算法,但高于其他3种算法。
对于12个测试函数,MPSO算法在10个函数上的优化平均值排名第一(包括并列),DEOPSO算法在4个函数上排名第一(包括并列),HPSOWM在3个函数上排名第一(包括并列),而CLPSO和SPSO算法在12个函数上的整体寻优精度不高,说明MPSO算法的寻优性能具有一定竞争性。

表3 高维多峰函数实验结果Tab.3 Experimental results of high-dimensional multimodal functions
图1为5种算法在测试函数上的适应度值收敛曲线。为便于观察,对适应度值做10为底的对数处理。由图1可知,在f1、f2、f3、f4、f6、f7、f9、f11函数上,MPSO算法的适应度收敛曲线呈现短小、间断的特征,曲线出现间断说明算法已经收敛到函数的理论极值0,对数真数为0时曲线不再显示,曲线呈现短小的特征说明MPSO算法与其他对比算法相比,收敛到函数最优值所使用的迭代次数较少。在函数f12上,MPSO算法与对比算法相比,在迭代后期能够挣脱局部极值的束缚,收敛到函数的理论极值0。
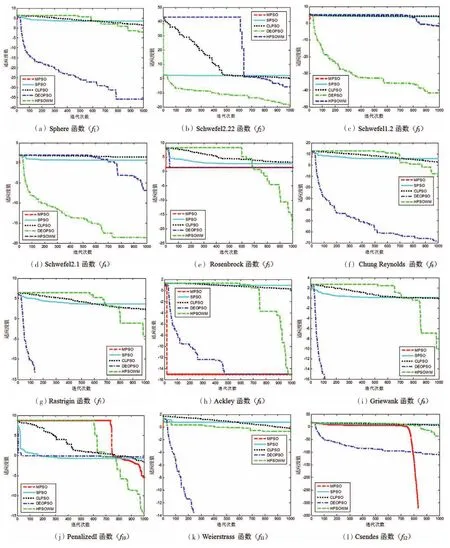
图1 5种算法的适应度收敛曲线Fig.1 Fitness convergence curves of five algorithms
综上所述,MPSO算法在包含高维多峰、高维单峰的12个经典测试函数上收敛精度和收敛速度均表现出良好的性能,在9个函数上均能收敛到函数的理论极值0,从适应度值的收敛曲线看,能够使用较少的迭代次数寻找到函数最优值,因此,MPSO算法提升了标准粒子群算法的收敛精度和速度。
3.2.2 固定精度下的收敛速度比较 最大迭代次数设为1 000,每个函数的预设精度在表1中列出。表4为固定精度下5种算法在12个测试函数上的平均迭代次数和寻优成功率。数值格式采用“平均迭代次数∕成功率”的表示方式。“1”表示成功率为100%。由表4可知,CLPSO、SPSO两个算法在12个函数上或不能收敛到预设精度,或收敛的成功率太低。HPSOWM算法在f5、f8、f10上收敛成功率达到
100%,在f6、f12上的收敛成功率分别达到70%和96%,而在其他7个函数上或不能收敛到预设精度,或收敛的成功率太低。MPSO算法在12个测试函数上均能100%收敛到预设精度。DEOPSO算法是新近效果较好的改进算法,其在函数f10上50次实验均不能收敛到预设精度,在其他11个函数上能够
100%收敛到预设精度。MPSO算法与DEOPSO算法相比,达到预设精度所使用的迭代次数大幅减少,除f5、f12外,在f5上,MPSO算法50次实验的收敛精度均值略低于DEOPSO算法,但在f12上MPSO算法在最大迭代次数为1 000次设定下,50次实验的收敛精度均值为0,优于DEOPSO算法。由此可以看出,MPSO算法在固定精度下的收敛速度较对比算法有明显提升。
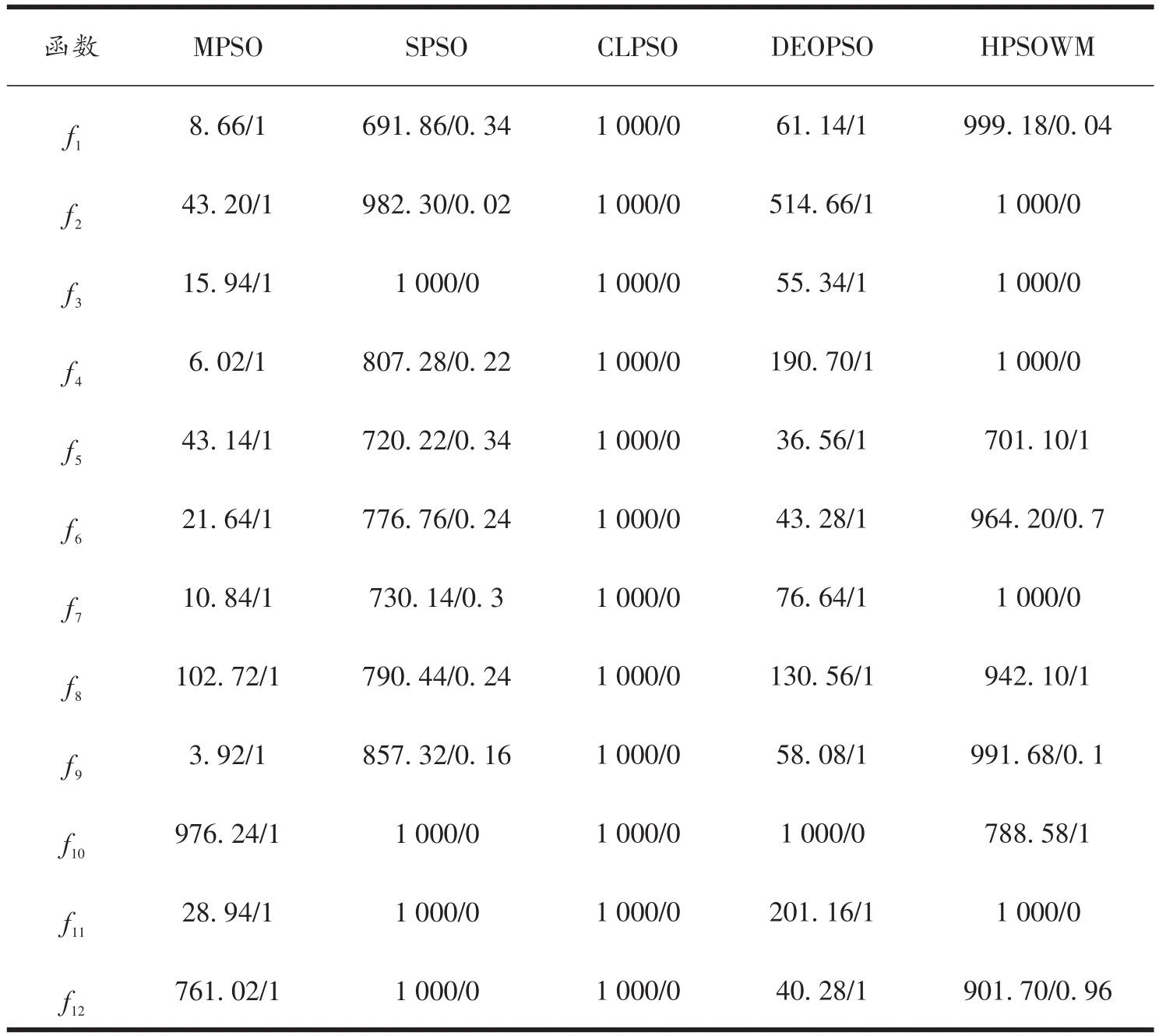
表4 固定精度下平均迭代次数与成功率Tab.4 Average number of iterations and success rate under fixed precision
3.2.3 时间复杂度分析 表5为5种算法在12个测试函数上,迭代次数固定为1 000,50次实验的平均运行时间(单位为s)。由表5可知,5种算法在12个测试函数上所用平均时间升序排名为MPSO、SP⁃SO、DEOPSO、HPSOWM、CLPSO。MPSO所用时间最短,说明通过对每代全局极值的各维度实施Morlet小波扰动作为被选择变异粒子的新位置,一方面通过全局极值的带领加快了算法收敛到最优值的速度,另一方面通过Morlet小波的微调作用有效防止了算法陷入局部最优。本文改进的变异策略只对每代全局极值进行小波变异,其计算复杂度小于CLPSO、DEOPSO、HPSOWM算法使用的策略。
3.2.4 MPSO在高维上的性能分析 从表1中选择6个测试函数,从两个方面做实验,分析MPSO算法在特别高维上的性能表现。一是分析MPSO算法在维度设定为1 000时,最差值、最优值、优化平均值、标准差4个指标的表现;二是将维度设定为100、300、500和1 000时,分析MPSO算法随着函数维度的增加,优化平均值的变化情况及其平均变化率。平均变化率[23]=∑((后一次维度的优化平均值-前一次维数的优化平均值)∕前一次维度的优化平均值)∕3。
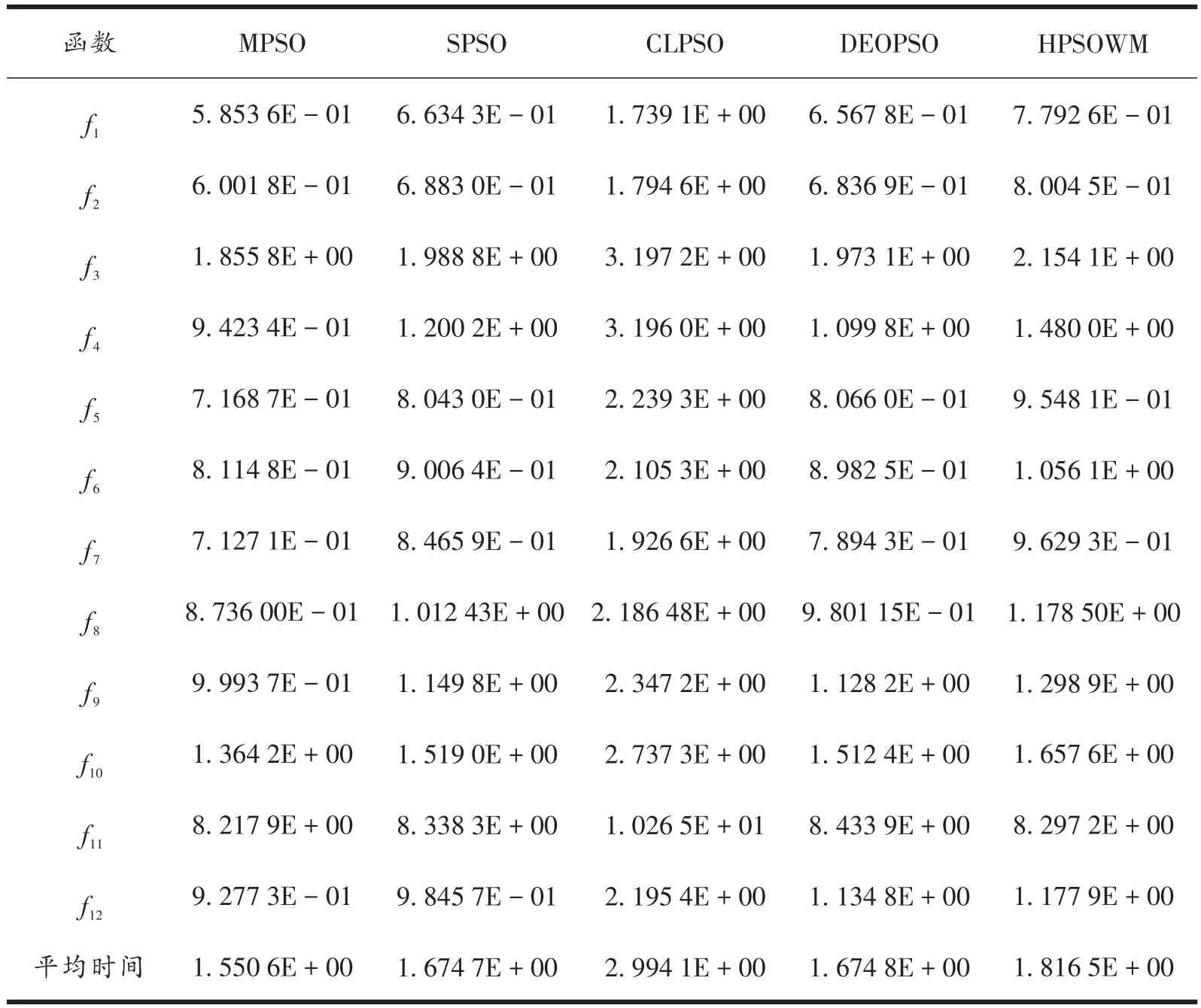
表5 5种算法的平均运行时间Tab.5 Average running time of five algorithms ∕s
表6为函数维度等于1 000时,MPSO算法在6个函数上,分别独立连续运行50次的实验结果。函数的变量取值范围越大,维度越高,寻找函数理论极值的难度就越大。由表6可以看出,MPSO算法在6个函数上的最差值、最优值、平均值及标准差均为0。说明在1 000维高维的情况下,MPSO算法仍能寻找到6个函数的理论极值。
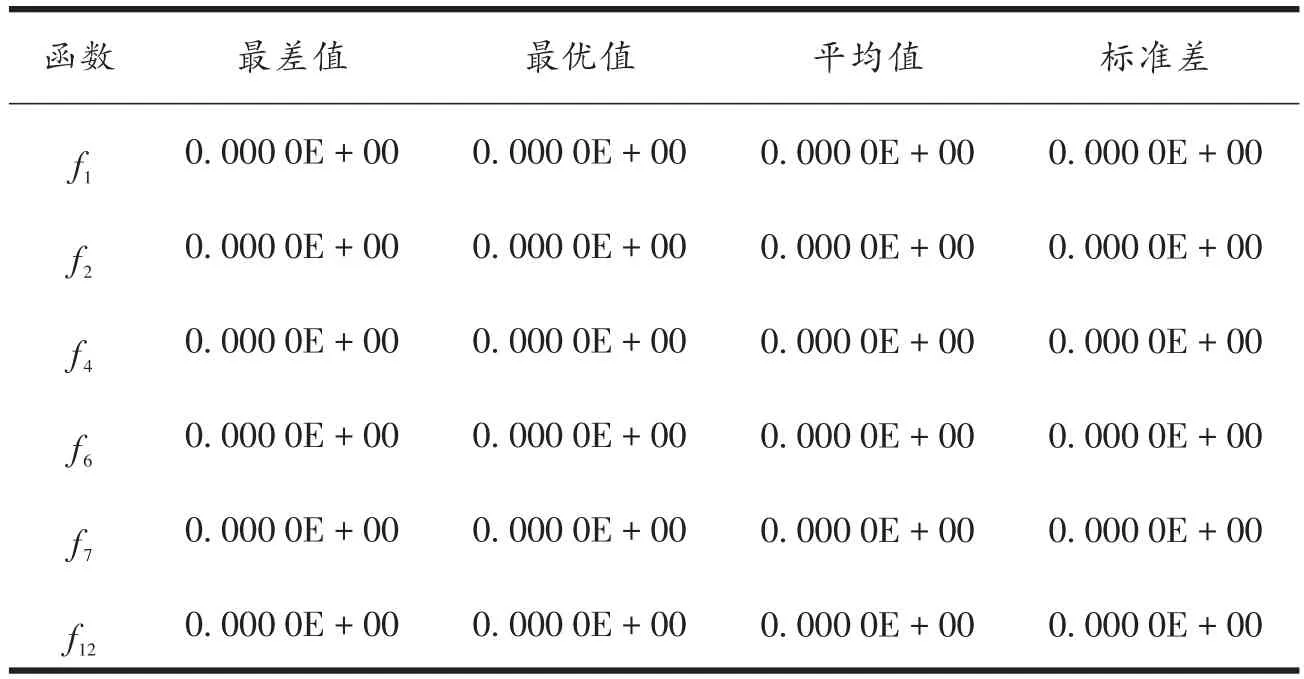
表6 MPSO算法在1 000维时的寻优结果Tab.6 Optimization results of MPSO algorithm in 1 000 dimensions
表7为MPSO算法在6个函数上,维度分别为100、300、500、1 000时,50次实验的优化平均值及优化平均值的平均变化率。从表7可以看出,MPSO算法在6个函数上随着维度的增加,MPSO算法的优化平均值都保持不变,均为函数的理论极值0。维度从100变化到1 000的优化平均值的平均变化率也为0。说明MPSO算法在选择的6个函数上的寻优性能随着维度的增加基本没有降低,从而进一步验证了本文所提改进策略的有效性。

表7 MPSO算法在不同高维上寻优结果Tab.7 Optimization results of MPSO algorithm in different high dimension
4 结语
本文改进的MPSO算法在12个经典测试函数上的寻优性能较SPSO有显著提升。在9个测试函数上的寻优结果大幅优于HPSOWM算法,在12个测试函数上的寻优结果优于CLPSO,在8个测试函数上的寻优结果优于DEOPSO算法。在较高目标精度下,较对比算法能够使用较少的迭代次数达到预设的目标精度。在6个函数上,在维度从100变化到1 000时,MPSO算法的优化平均值都保持不变,每次均能收敛到函数的理论极值。从而表明,对每代粒子种群的全局极值各维度实施Morlet小波扰动,将扰动结果作为被选择变异粒子的新位置,能够引导粒子快速收敛到最佳位置,并帮助粒子跳出局部极值的干扰,从而有效提升了算法的收敛精度和收敛速度。由于本文选择的函数有限,对于MPSO算法在其他更复杂函数优化上的性能表现有待进一步研究。
参考文献(References)
[1] KENNEDY J,EBERHART R C.Particle swarm optimization[C]∕∕Proceedings of IEEE International Conference on Neural Net⁃works.Perth,Australia:IEEE,1995:1942-1948.
[2] SHI Y H,EBERHART R C.A modified particle swarm optimizer[C]∕∕Proceedings of IEEE International Conference on Evolu⁃tionary Computation.Anchorage,USA,1998:69-73.
[3] TAMBOURATZIS G.Applying PSO to natural language processing tasks:optimizing the identification of syntactic phrases[C]∕∕Proceedings of 2016 IEEE Congress on Evolutionary Computation.IEEE,2016:1831-1838.
[4] NGAN M S,TAN C W.Photovoltaic multiple peaks power tracking using particle swarm optimization with artificial neural net⁃work algorithm[M]∕∕Advances in solar photovoltaic power plants.Berlin:Springer,2016.
[5] 刘锐,李铁萍,周国强,等.适用于核动力设备故障诊断的改进粒子群优化算法[J].动力工程学报,2017,37(10):837-841,854.
[6] 刘奇,周力,周雅.基于混合粒子群优化算法的ZnO镀膜光纤传感器的相位偏移[J].光学学报,2017,37(1):263-270.
[7] MENDES R,KENNEDY J,NEVES J.The fully informed particle swarm:simpler,maybe better[J].IEEE Transactions on Evo⁃lutionary Computation,2004,8(3):204-210.
[8] LIANG J J,QIN A K,SUGANTHAN P N,et al.Comprehensive learing particle swarm optimizer for global optimization of multi⁃modal function[J].IEEE Transactions on Evolutionary Computation,2006,10(3):281-295.
[9] ZHAN Z H,ZHANG J,LI Y,et al.Adaptive particle swarm optimization[J].IEEE Transactions on Systems,Man,and Cyber⁃netics-Part B:Cybernetics,2009,39(6):1362-1381.
[10]马国庆,李瑞峰,刘丽.学习因子和时间因子随权重调整的粒子群算法[J].计算机应用研究,2014,31(11):3291-3294.
[11]皮倩瑛,叶洪涛.一种动态调节惯性权重的粒子群算法[J].广西科技大学学报,2016,27(3):26-32.
[12]高卫峰,刘三阳,焦合华,等.引入人工蜂群搜索算子的粒子群算法[J].控制与决策,2012,27(6):833-838.
[13]任聪,葛洪伟,杨金龙,等.引入混合蛙跳搜索策略的人工蜂群粒子群算法[J].计算机工程与应用,2015,51(22):38-41.
[14]KENNEDY J.Bare bones particle swarms[C]∕∕Proceedings of the IEEE swarm Intelligence Symposium.Indianapolis,IN,USA, 2003:80-87.
[15]CAMPOS M,KROHLING R A,ENRIQUEZ I.Bare bones particle swarm optimization with scale matrix adaptation[J].IEEE Transactions on Cybernetics,2014,44(9):1567-1578.
[16]YANG Z,YANG Y,YANG H,et al.An improved particle swarm optimization method based on chaos[C]∕∕International Confer⁃ence on Natural Computation.IEEE,2014:67-81.
[17]李俊,汪冲,李波,等.基于扰动的精英反向学习粒子群优化算法[J].计算机应用研究,2016,33(9):2584-2587, 2591.
[18]LING S H,IU H H,CHAN K Y,et al.Hybrid particle swarm optimization with wavelet mutation and its industrial applications[J].IEEE Transactions on Systems,Man,and Cybernetics-Part B:Cybernetics,2008,38(3):743-763.
[19]JIANG F,XIA H Y,TRAN Q A,et al.A new binary hybrid particle swarm optimization with wavelet mutation[J].Knowledge-Based Systems,2017,130:90-101.
[20]高东慧,董平平,田雨波,等.一种改进的小波变异粒子群优化算法[J].计算机工程,2012,38(21):145-147.
[21]石永生,高浩,陈家琪.基于小波变异的粒子群算法[J].计算机工程与设计,2011,32(2):693-695,699.
[22]程慕鑫,刘漫丹,夏伟.基于小波变异的改进粒子群算法[J].华东理工大学学报(自然科学版),2013,39(1):90-94.
[23]肖辉辉,万常选,段艳明,等.基于引力搜索机制的花朵授粉算法[J].自动化学报,2017,43(4):576-594.
