基于本征正交分解的环境温度分布快速预测模型研究

芮庆，王路瑶，José Alberto García Fernández，杜志敏，晋欣桥

（上海交通大学制冷与低温工程研究院，上海 200240）

0 引言

人员感知的热舒适度受到室内的空气温度和速度分布的影响，丹麦学者FANGER[1]指出，送风温度过低将产生“冷感”，送风速度过高则给室内人员带来“吹风感”。送风温度和送风量不仅影响人员的热舒适，两者的设定值还分别影响着冷水机组和风机的能耗[2]。以冷水机组和风机等设备为主的空调系统能耗在建筑能耗中约占65%左右[3]。因此，良好的送风量或送风温度控制策略将表现出可观的节能潜力[4]。而任何控制策略都需要建立在保证室内人员热舒适度的基础之上，于是对室内温度场的快速预测格外重要，室内的温度分布将给送风温度和送风量的动态优化设定提供参考，帮助达到降低空调系统能耗的目的[5]。

计算流体力学（Computational Fluid Dynamics，CFD）模拟常用来预测温度场分布[6]，CFD 能够借助计算机的快速计算能力，离散求解流动控制方程[7-10]。刘巧玲等[11]使用Fluent 软件研究了VAV 空调系统中温度传感器的布置位置对室内的温度场和速度场的影响。徐培璠等[12]在TRNSYS-CFD 仿真平台上研究了独立新风系统的送风量对气流组织和人员热舒适度的影响。但使用CFD 模拟方法需要消耗大量的时间成本和计算成本。流动模拟过程将占用大量的存储空间用于加载模拟软件以及算例的网格数据，并将消耗大量的计算资源用于对流动及传热控制方程的离散迭代求解，因此要求计算设备有较高的硬件配置。

为了提高对温度分布的模拟响应速度，减少流动模拟过程中占用的计算资源和内存空间，引入基于数据挖掘方法的本征正交分解（Proper Orthogonal Decomposition，POD）降阶模型完成对建筑物内的热环境模拟。POD 将提取数据集中所隐藏的各阶特征模态，通过模态叠加来重构数据集所表征的高维物理场。聂春生等[13]使用POD 方法完成了对复杂外形飞行器热环境的快速预测。陶文铨等[14]将正交分解技术运用到湍流问题中，非常准确和快速地得到问题的解。SAMADIANI 等[15]使用降阶建模方法建立了数据中心的热力模型，对数据中心内的热环境进行了研究。相比于CFD 模拟，正交分解方法可以脱离流动模拟的软件环境，占用极少的计算资源和内存，并能迅速地获取室内的温度场或速度场分布。

1 研究对象及其CFD模型

选择某写字楼中的一层办公室房间作为研究对象，办公室的东墙作为唯一的外墙体与室外环境换热，其余墙体均为用于分隔的内墙，假设各房间的温度设定同步，内墙两侧无热量流动。该办公室的空间大小为12.8 m×8.6 m×3.9 m，共设工位12 台，每台工位配置有办公桌椅和散热功率为150 W的台式计算机，LED 平板灯工作时产生的灯光负荷纳入天花板边界。房间使用顶送顶回的VAV 空调系统，尺寸为0.5 m×0.5 m 的送风口和尺寸为1 m×0.5 m的回风口均内嵌于房间的天花板中。在建模过程中，将人员、桌椅和计算机简化为对应大小的长方体，人员的散热量按照静坐状态选为1MET。房间的三维空间布置如图1所示。

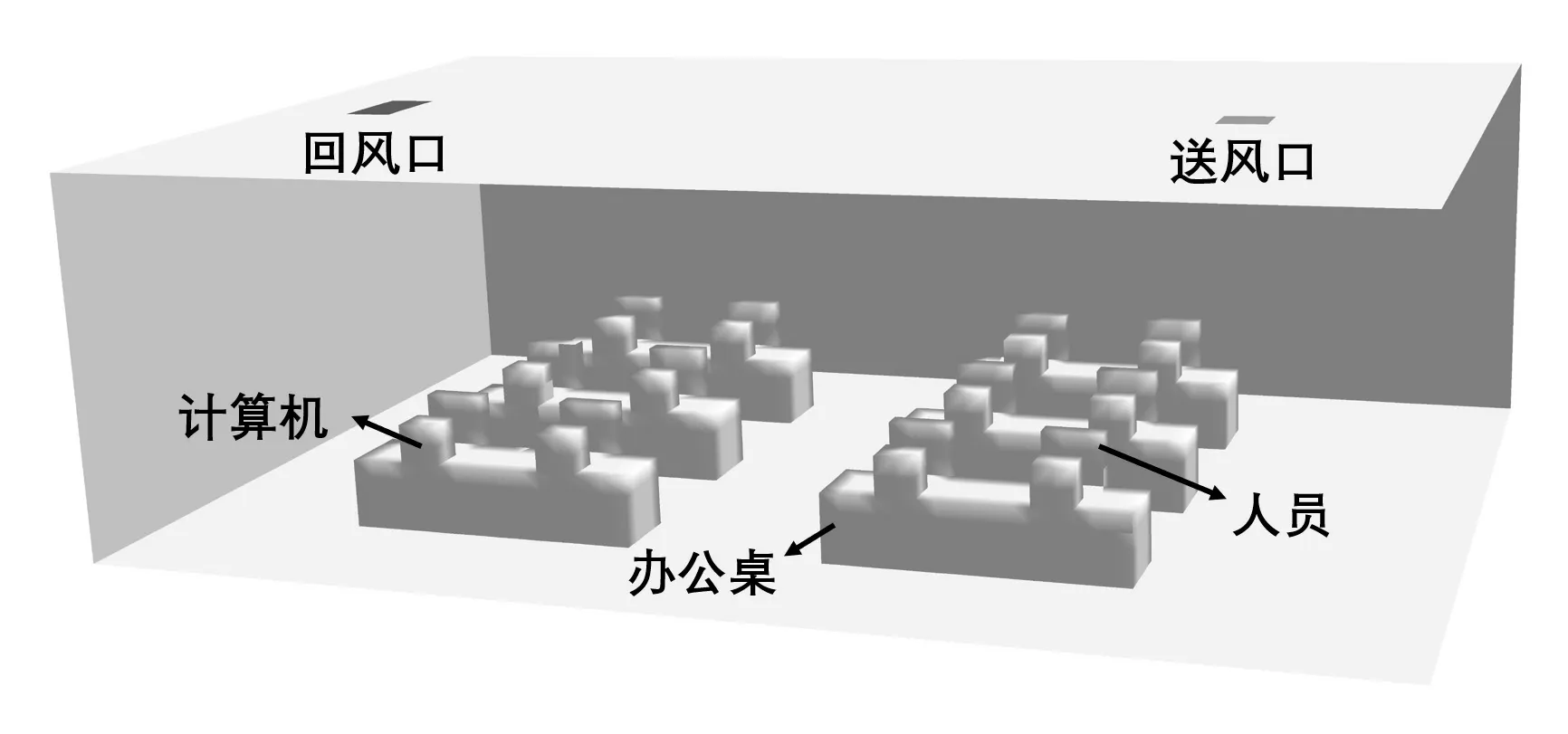
图1 办公室房间布置三维视图

房间的回风温度为25 ℃，使用冷负荷系数法计算房间的空调冷负荷为7.3 kW。其中通过东墙传入室内的逐时冷负荷曲线如图所示，选取19 时的冷负荷558.24 W 设定为东墙的定热流边界条件。根据送风温度的不同，设定6 个观测状态：8 ℃、10 ℃、12 ℃、14 ℃、16 ℃和18 ℃。由下式可知，空气提供的冷量应和房间需要的冷负荷相等[16]。

在送风过程中，将低速空气视为不可压缩流体，并忽略空气通过门窗产生的渗漏，假定围护结构绝对密闭。空气的温度、速度、压强和其他物理量之间互相影响，它们的作用关系需要同时满足两个守恒条件：质量守恒和动量守恒。Navier-Stokes方程以数学解析形式描述了流体的这两种约束条件[17]。

选择标准k-ε雷诺平均N-S 方程模拟房间内的湍流运动，使用SIMPLE 算法对压力和速度进行耦合求解[18]。流动仿真的各处边界条件设置见表1。

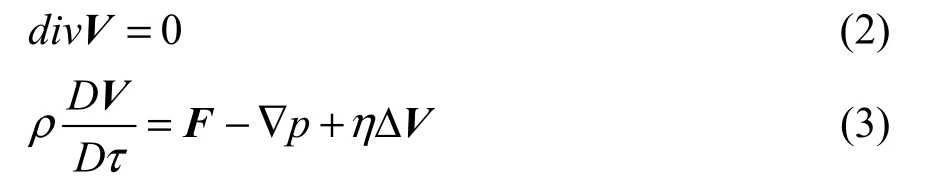
式中：

ρ——体密度，kg/m3；

τ——时间参数，s；

V——速度矢量，m/s；

F——场中作用力矢量，N；

η——流体的动力粘度，N·s/m2；

div——散度算符；

Δ——Laplace 算子。

空气的低速不可压流动过程还需满足对流传热能量微分方程[19]：

式中：

cp——流体的定压比热容，J/(kg·℃)；

T——流体温度，℃；

λ——流体的导热系数，W/(m·K)；

∇——Nabla 算子。

表1 流动模拟的边界条件设置

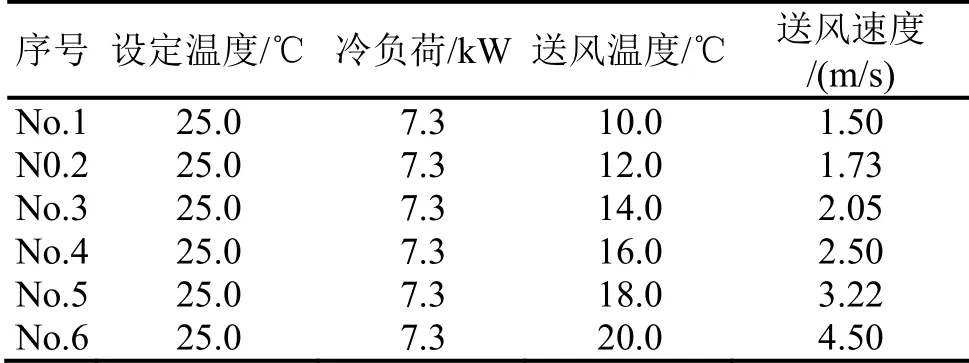
表2 CFD 仿真的观测状态设定

在网格创建和边界条件设定后，设定如表2所示的6 组观测状态，使用CFD 软件仿真得到建筑物内部流域的温度场分布。图2展示了不同的观测状态下，办公室房间内Y=4.3 m 截面上的温度分布情况。所有观测状态生成的温度信息将用于本征正交分解模型的训练。

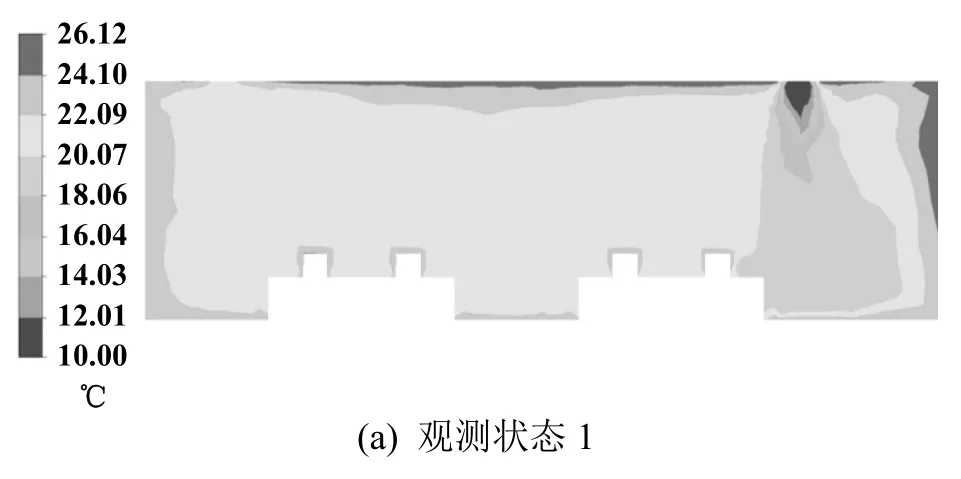
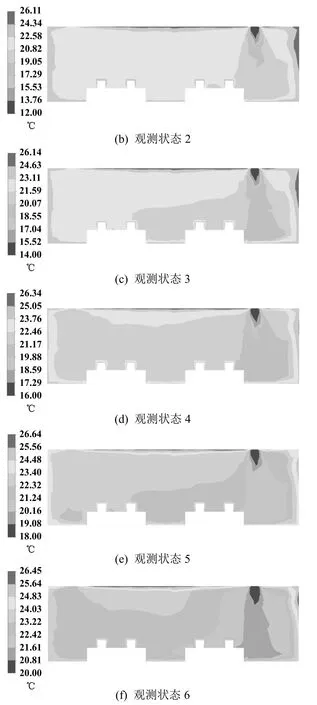
图2 观测状态下的温度分布云图

2 POD模型的建立

本征正交分解模型也被称为POD 模型，它在观测到的物理场分布的基础上得到对应于历史数据的一系列模态，CFD 模型生成的温度场数据集将作为POD 模型的训练样本集。由于其基于数据的方法特性，产生的各阶模态能够很好地描述非线性系统，故POD 模型可以很好地适用于湍流流动的描述[20]。可以通过对所得到的模态的使用更高效地预测物理场分布情况。假设第i次观测到的物理场分布是Ti(x)，则可以将其表示为历次观测的物理场平均分布(x)和绝对偏差矩阵τ(x)之和：

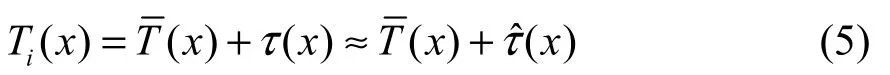
绝对偏差矩阵τ(x)可以以关于模态ϕ的无穷级数形式展开，c是对应于每个模态的模态系数。考虑到实际应用的情况，截取并保留无穷级数中的前Ns项模态组成近似偏差矩阵ˆ()xτ，并约束模态集满足正交性条件：

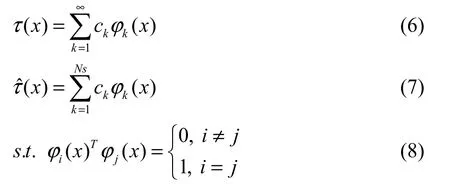
为了提高模态截取过程的精度，前Ns项模态的选择应使得近似偏差ˆ()xτ和绝对偏差τ(x)间的误差最小，选用二阶范数构造误差表达式，近似偏差矩阵中ϕk的确定应使的二范数最小：

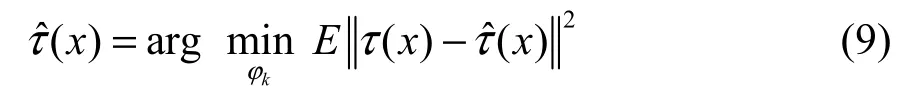
因此，在对绝对偏差矩阵展开得到的无穷级数的选择过程中，产生的截断误差可以表示为：

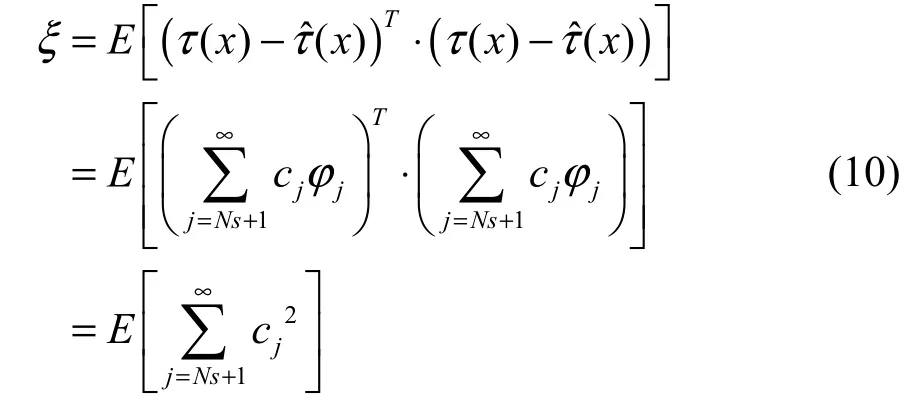
对于模态系数c，由模态满足的正交性条件可以得到另一种表达形式：

将模态系数代入到截断误差中，并构造R=E(ττT)，则截断误差可写作关于模态和偏差的形式：

因为模态集受正交性条件约束，所以模态ϕ的选择转化为条件极值求解问题。使用拉格朗日乘数法构造拉格朗日函数L(ϕj)求解模态的截断误差极值：

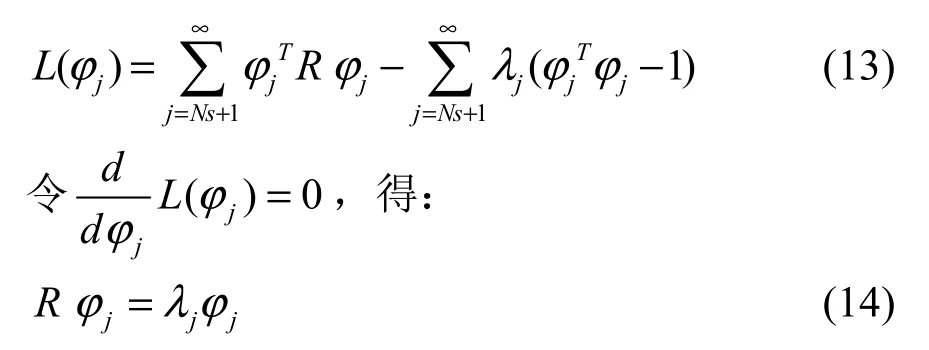
式中j=Ns+ 1,Ns+ 2,…。

观察R阵的性质，由R=E(ττT)可以得到：

即R是实对称阵，由实对称阵的性质可以得到：

故物理场的模态求解转化成R阵的特征值问题，ϕk是R阵的特征向量。

特征值λ表征着对应模态在高维非线性系统中捕捉到的能量的大小[21]。在应用过程中，可以将特征值作为依据，按照应用情形设定的重构误差阈值ε，在模态集中按照能量次序截取前Np阶模态。

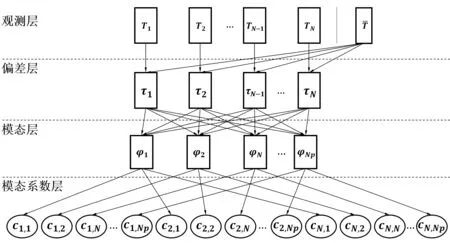
图3 POD 模型的数据流图

3 POD模型的训练过程

选择房间内Y=4.3 m 截面上的温度分布数据集作为模型的训练数据来源，截面尺寸为12.8 m× 3.9 m。图中划分的蓝色单元格大小为0.128 m× 0.128 m，将每个节点作为一支虚拟温度传感器，经过6 次观测，共获得16,326 组温度信息。在截面上选择3 条观测路线L1、L2、L3，如图4所示，每条观测路线上均分布着观测节点，观测节点的总数为180 个。不断变换观测状态，获取观测节点上的温度信息作为训练数据集。通过遍历观测状态对温度信息进行迭代收集的流程如图5所示。

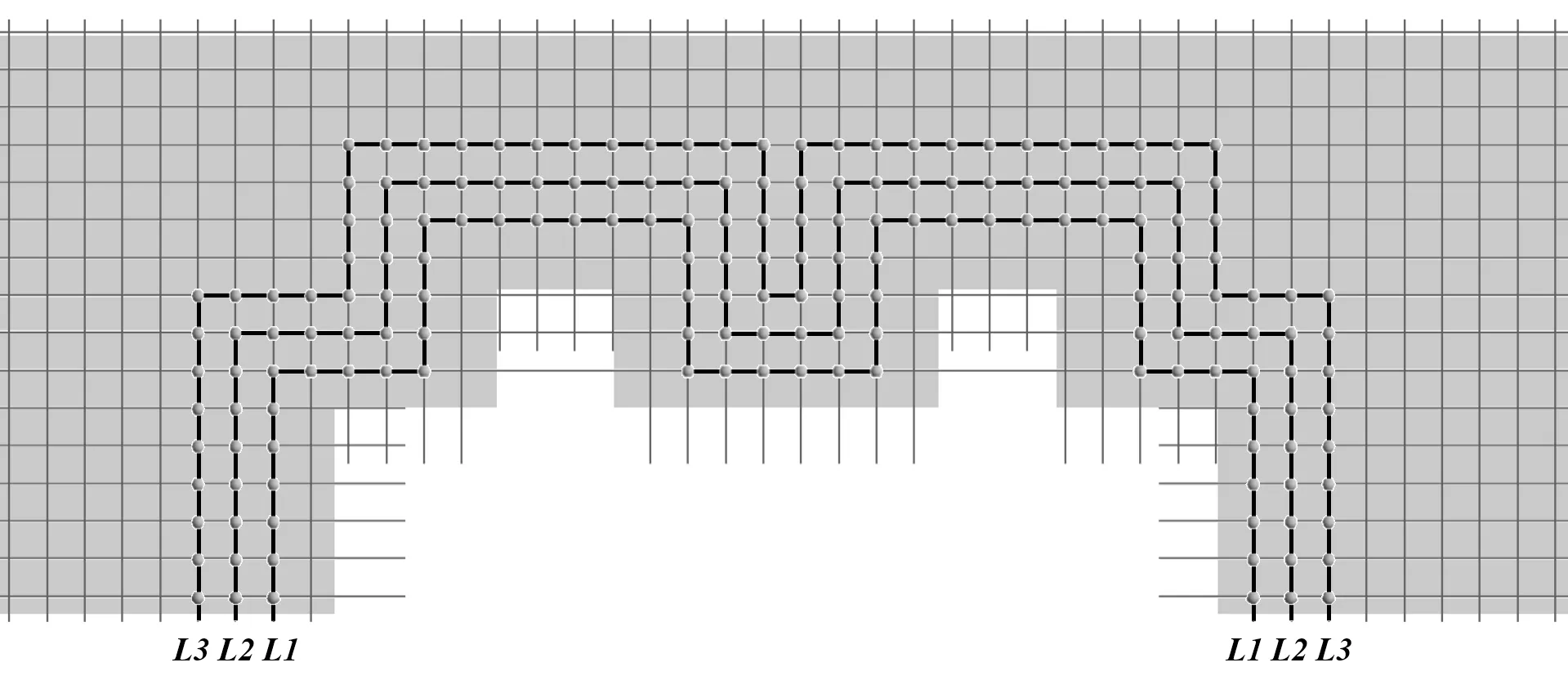
图4 观测路线的设定示意图

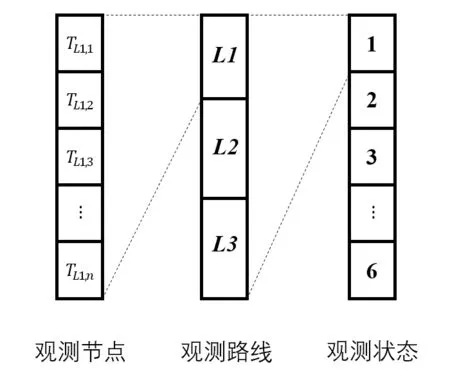
图5 POD 训练过程的数据流图

将获得的各观测状态的温度数据存入观测层矩阵T，得到：

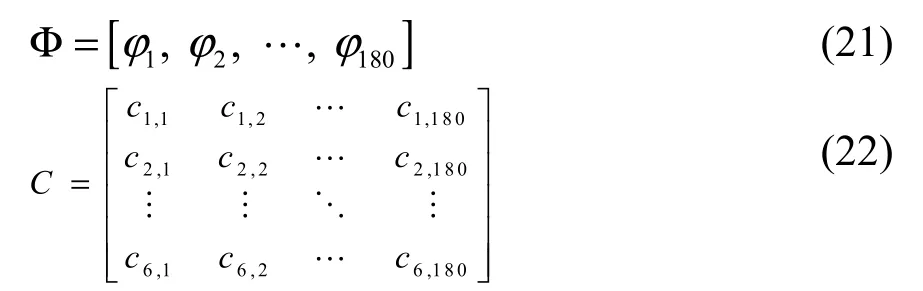
经过POD 模型的训练，得到当前温度数据集空间的正交模态集合Φ和各个状态的模态系数集合C：

其中，对应于各阶正交模态的特征值按照能量大小排序如图6所示，可以看出，前6 阶特征值携带的能量急剧下降，前6 阶特征值与其余阶特征值在数量级上有着显著的差别，并从第7 阶开始，特征值携带的能量趋于稳定。

假设对模态进行截取时，选择前Np阶模态用于训练本征正交分解模型，定义POD 模型的重构误差()Npδ用于衡量模态截取对温度分布重构的准确度：

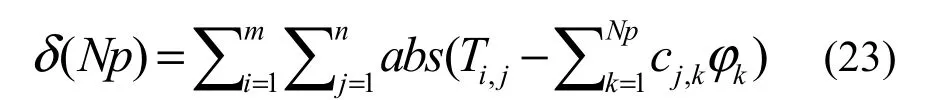
式中，m表示观测状态，n表示观测节点。

从表3中可以看出，随着Np的增加，模态截取产生的误差逐渐减小，并且从第7 阶模态开始，重构误差()Npδ趋于收敛。计算前6 阶模态对应的特征值在样本的特征值集合中的能量占比：

故综合考虑重构误差和能量占比，选择前6 阶特征值对应的模态用于捕捉研究对象在流动和换热过程中的温度分布特性，并以截断得到的前6 阶模态构建POD 模型，用于房间对象的温度场重构和温度分布预测。

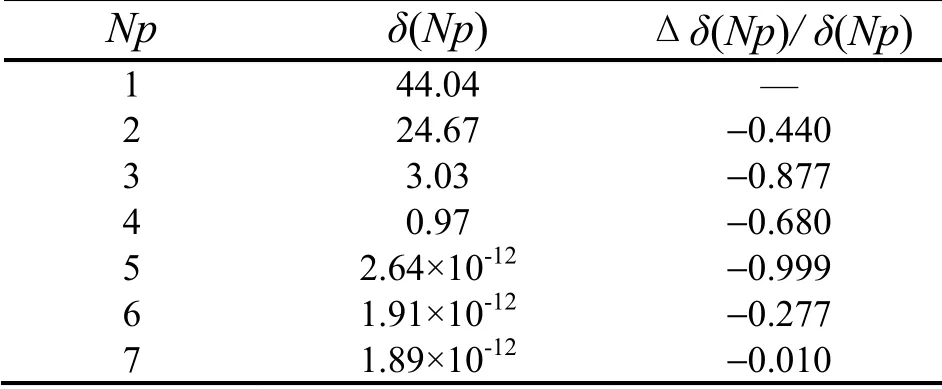
表3 模态截取后的重构误差分析

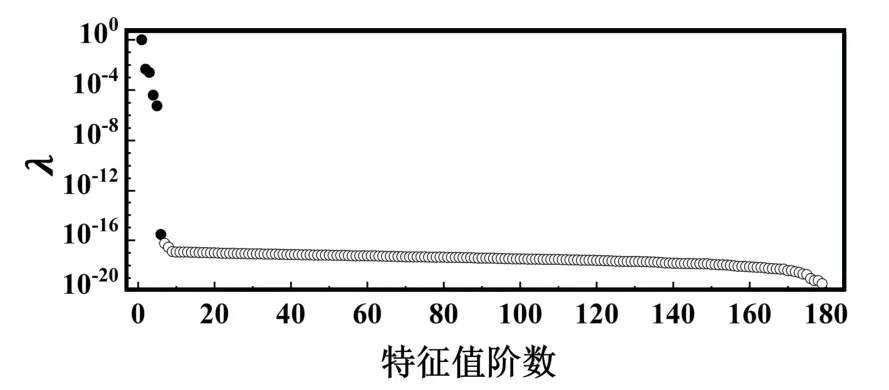
图6 按能量排序的POD 模型特征值

用于温度场重构的前6 阶特征值对应的模态分布如图7所示。

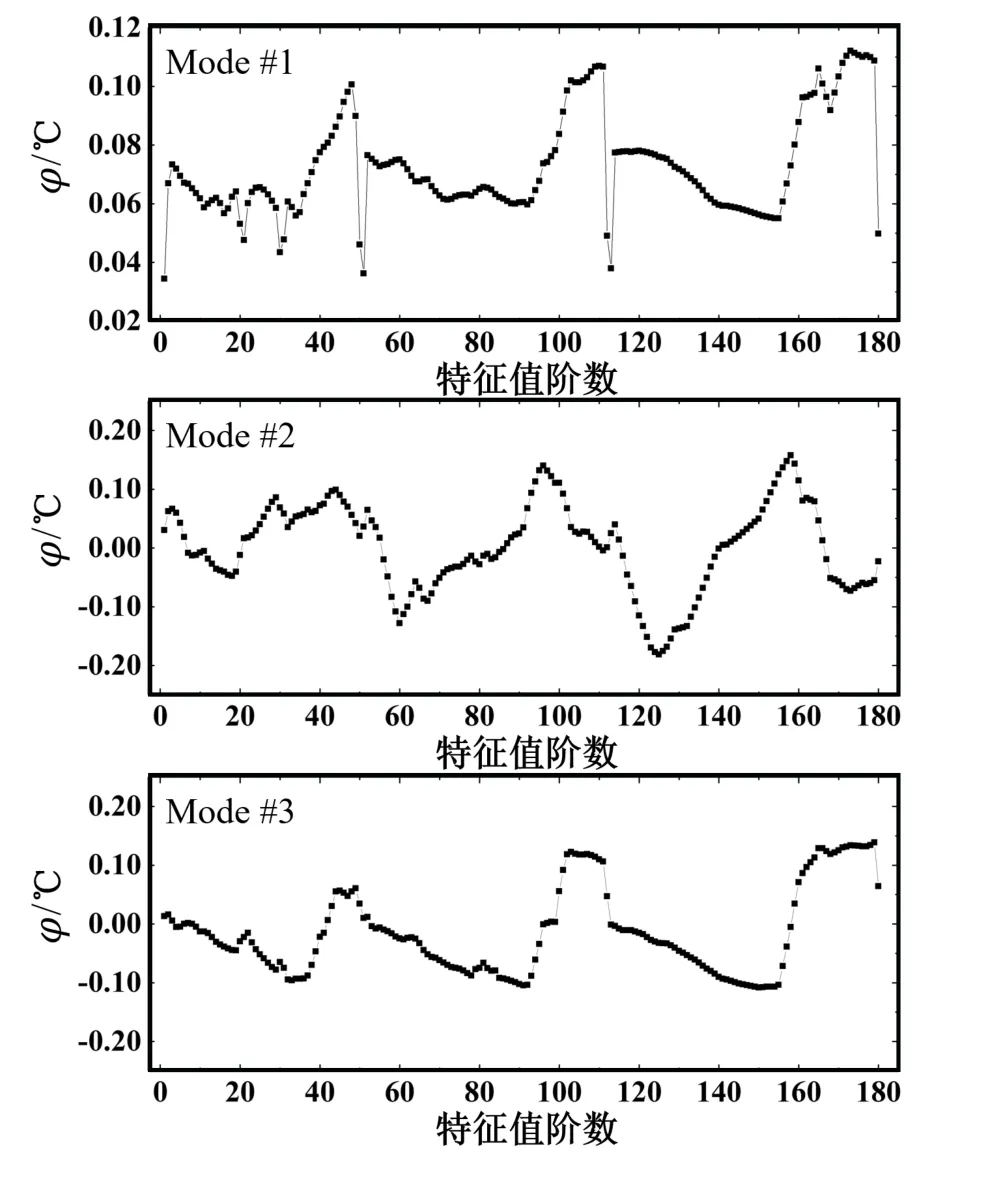
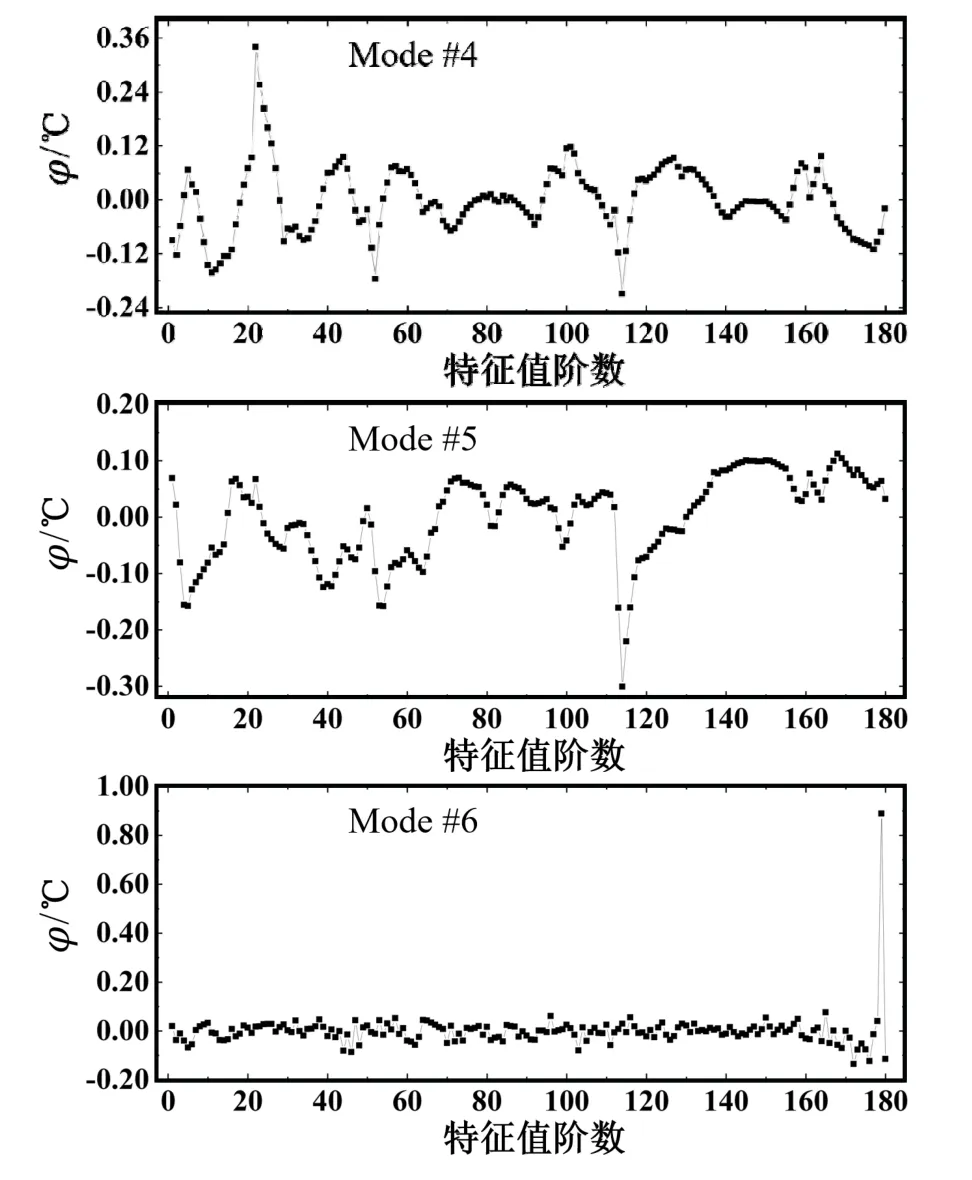
图7 前6 阶POD 模态分布

在选定的6 阶模态下，每次观测状态对应于每阶模态的模态系数分布情况参见图8。可以看出，有着较大能量占比的特征值对应的模态在温度场重构中起到主要作用。

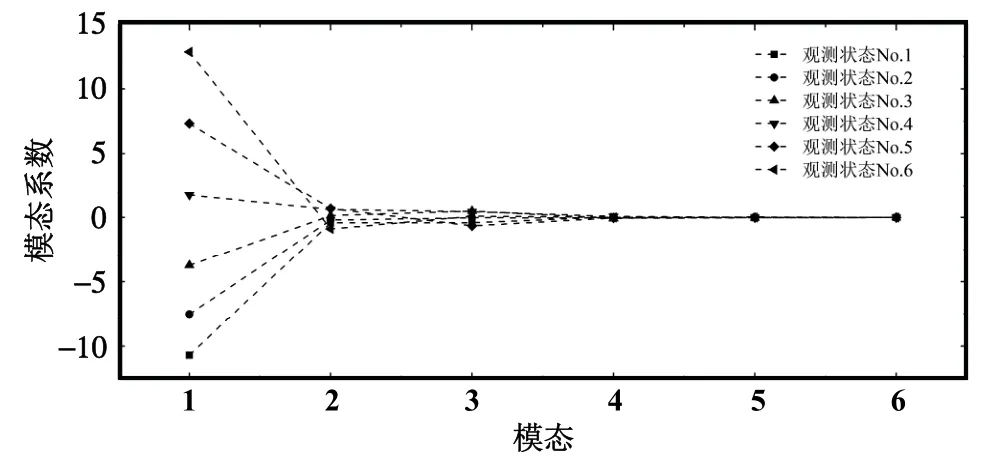
图8 POD 模型的模态系数变化

4 POD模型的泛化分析

因为流动的连续性，全空间的温度场模拟依赖于整体流域。即使仅仅关注观测路线上的温度分布，仍然需要对房间内的所有空间数值求解。也就是说，CFD 仿真方式存在着大量的信息冗余。

本征正交分解模型从数据中学习样本空间的模态，在获取模态之后，通过模态的叠加重构即可预测房间的温度分布。

相比于重新设置边界条件对离散的流动和传热方程进行CFD 求解的方式，POD 的模态重构将极大地节省预测时间和计算资源。

由Karhunen-Loeve 分解的数学推理过程可知，模态截断是POD 模型的误差来源。设定一组测试状态Mtest用于校验POD 模型预测温度分布时的泛化能力。

图9给出了在送风温度为11 ℃的测试状态下，观测点位置上使用POD 模型预测得到的温度分布和通过CFD 仿真方式得到的温度分布。图10展示了在5 种测试状态下，相比较于CFD 模型，使用POD 模型生成温度分布时所产生的泛化误差。

分析5 种测试状态下使用POD 模型预测温度分布所产生的预测误差，计算泛化误差的标准差和方差分布如表4所示。

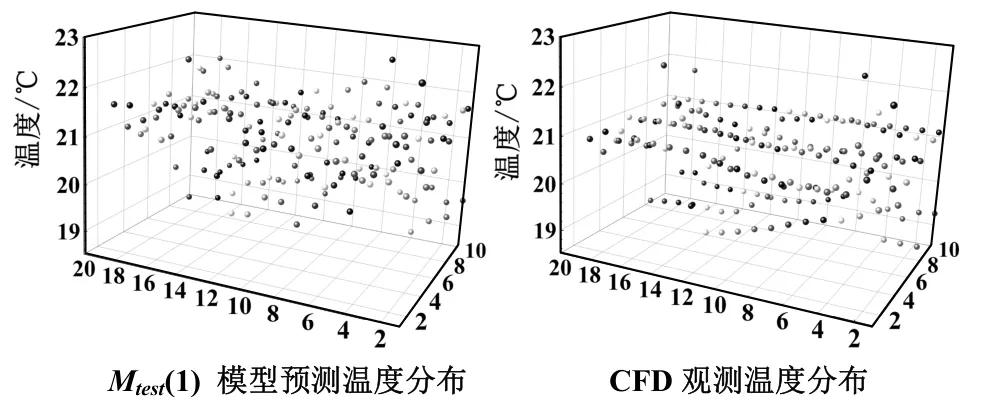
图9 POD 预测和CFD 仿真结果对比（送风温度11 ℃）

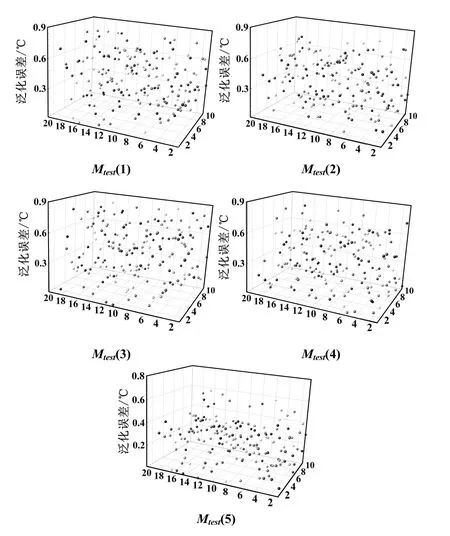
图10 POD 模型的泛化误差分析

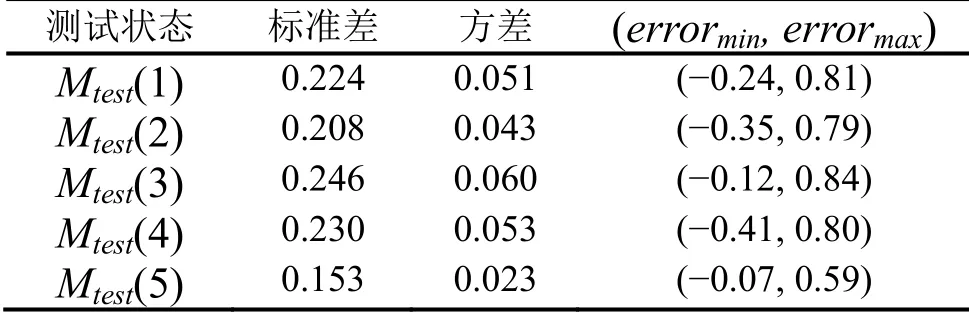
表4 POD 模型的泛化误差

用于流场仿真和POD 模型泛化的计算机配置有Pentium®Dual-Core CPU，频率为2.80 GHz，内存2,048 MB。通过CFD 仿真的方式获取房间内的温度场，每步迭代需要传递5.382 MB 的网格数据，平均每次仿真用时92.76 s。POD 模型每次需要加载模态信息，6 个模态数据占用的内存大小为13.1 KB，平均每次泛化用时为6.204 ms。

POD 模型在测试样本空间中的泛化准确度ε表示为：

在5 组测试状态中，ε≈95.3%，其温度场预测的准确度接近基于流动控制方程离散求解的结果。需要注意的是，POD 模型的计算速度远远超出对流动和传热方程离散迭代求解的速度。也就是说，POD 模型不仅在训练数据之外的样本空间中有着良好的泛化能力，同时该途径的温度场预测过程需要的计算成本和内存成本非常微小。因此，相比于CFD 仿真的方式，基于Karhunen-Loeve 分解的本征正交分解模型表现出更高效的温度场预测性能。

5 结论

本文提出了使用本征正交分解模型用于预测房间内指定位置上温度分布的方法，并将预测结果和通过流动及传热仿真得到的温度分布进行对比分析。使用6 组观测状态数据作为POD 模型的学习样本，从中获得当前研究对象在流动和传热过程中的各阶模态，用于温度场的重构预测。设定测试状态检验数据驱动型的POD 温度预测模型的泛化能力，结果显示，POD 模型能够比较精确地描述研究对象的流动和换热过程，从而表现出良好的温度分布预测准确度，同时，POD 模型直接使用从训练样本中提取到的模态数据用于温度场的重构，跳过了对流动及传热控制方程的离散差分和在指定误差限内的迭代求解过程，因此具有更加快速的预测响应速度和更少的内存空间。由于使用了基于Karhunen-Loeve 分解的数据挖掘方法，POD 模型具有广泛的通用性，本征正交分解作为数据驱动型的温度预测方法，可以在不同的研究对象上被扩展和使用，不仅能使温度分布预测过程更加敏捷，更增加在物联网环境下移植此种预测方式至智能硬件上的可行性。