长昆客运专线铁路路堑边坡监测数据预处理方法

2018-04-16郭帅杰宋绪国隋孝民庄仲欣

铁道标准设计 2018年4期

郭帅杰,宋绪国,隋孝民,庄仲欣,张　磊

(1.中国铁路设计集团有限公司,天津　300251； 2.城市轨道交通数字化建设与测评技术国家工程实验室,天津　300251)

1　研究背景

长昆客运专线为沪昆客运专线西段主要组成部分，位于湖南、贵州和云南境内，区段列车最高时速250 km，并预留提速条件。其中，长沙至玉屏区段主要为山地丘陵地貌[1]，部分线路以高路堑边坡形式通过，线路中心最大挖深27.5 m，最大路堑边坡高度为42 m。

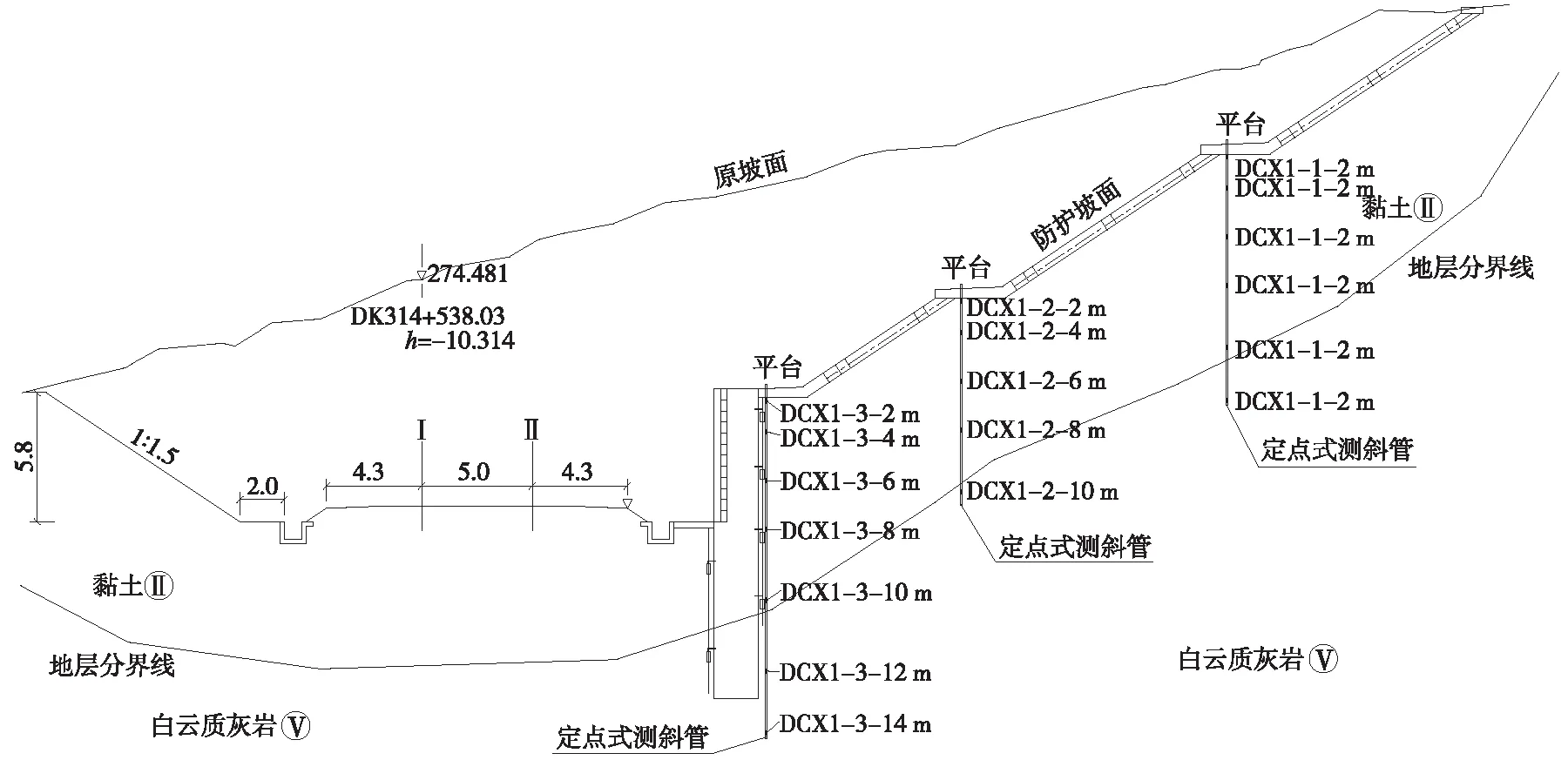
图1　监测断面1及定点式水平位移计埋设情况(单位：m)

长昆客运专线长沙至玉屏段现场监测方案设计中，于湖南省怀化市中方县境内的典型区段设置4个路堑边坡位移监测断面(DK314+538、+541、+544、+582)，进行坡面位移、深层水平位移和桩体前后土压力的自动监测，每天固定时间实时传输监测数据。监测结果表明，4个断面埋设元器件监测数据时程曲线均表现出明显的跳跃性、无序性特点，既无法预测路堑边坡位移发展趋势，也无法判定其稳定状态，若不进行必要的还原和平滑处理[2-5]，现场实测数据并无实际指导意义。为提高路堑边坡自动监测数据预警预报和边坡安全状态评估能力[6-8]，通过定点式水平位移计监测数据还原和平滑降噪处理，研究路堑边坡自动化监测数据预处理方法。

2　长昆客运专线路堑边坡位移监测结果

2.1　工程监测断面情况概述

长昆客运专线长沙至玉屏段路堑边坡监测段位于新建乡特大桥与黄板桥1号大桥间，采用挖方方式通过山包腰部，地形起伏较大，地表植被茂密，植被以灌木和杂草为主，其中，DK314+767～DK316+700区段内存在断裂。路堑边坡浅层为弱膨胀性的褐黄色硬塑黏土，层厚2～10 m；深层为岩体较为完整的弱风化、中厚层状分布的白云质灰岩，岩层产状131°∠54°，中线走向258.6°，右侧顺层。区段内岩溶发育等级为中等发育，地下水为第四系孔隙潜水、碳酸盐裂隙岩溶水和浅变质岩裂隙水，大气降水补给为主，埋深为4.5～13.5 m。

长沙至玉屏段路堑边坡现场监测方案设计中，共布设DK314+538(断面1)、+541(断面2)、+544(断面3)、+582(断面4)4个监测断面，监测断面1及定点式水平位移计埋设情况如图1所示，其他断面元器件埋设情况与断面1基本相同。水平位移点编号DCX1-1-2 m表示第1个监测断面上第1个平台处距孔口高程为2 m位置处的位移计监测点，监测数据初始接收时间为2013年10月16日。

2.2　平台水平位移原始监测结果

根据1～4监测断面临近坡面位置处的水平位移计原始监测数据，整理得到各监测点位置的原始水平位移时程曲线，如图2所示。图2中各监测断面坡面附近的水平位移测点时程曲线均表现为十分明显的跳跃性、无序性特点，并不能直接作为边坡稳定状态的评估依据。其中，监测时间进入260～400 d区域时，受外部环境或采集仪误差等因素的影响，各测点水平位移时程曲线均进入强扰动期，说明此阶段外界因素出现强烈变化，同时影响4个监测断面的各位移监测点，此外，对比现场监测的土压力、坡面位移计监测结果，该时间段内数据亦出现明显异常，初步判定现场多通道集成数据采集仪出现采集误差。

图2　各断面水平位移计原始监测曲线

由于各测点水平位移并无明显变化趋势，无法进一步预测或评估边坡稳定状态，若不进行原始监测数据的预处理[9-10]，监测数据将失去其实时反馈和现场预警意义[11-12]。因此，必须采用一定的平移还原、奇异点剔除还原和平滑降噪处理方法，得到边坡各测点接近于真实变形状态的水平位移时程曲线，满足边坡位移发展趋势预测和稳定性评价要求。

3　原始监测数据的平移还原与插值

3.1　监测数据的平移还原

图2中包含了4个断面共11个测点的水平位移时程曲线，为简化分析工作量，本文以DCX1-2-2、DCX2-1-2和DCX4-2-2三个测点为例完成原始监测数据的还原，还原结果如图3所示。其中，DCX1-2-2测点于260 d和360 d时间位置处于短时间内出现大幅度突变，DCX2-1-2测点于206 d位置处出现突变，分别通过平移方法得到相应还原曲线。DCX4-2-2测点时程曲线整体变形趋势满足路堑边坡的一般规律，但于260 d和400 d附近时间区域出现突变，存在短时间的大量异常数据点，通过异常点剔除方法，得到了接近于路堑边坡实际变形规律的还原曲线。

图3　三测点原始曲线的还原结果

3.2　还原曲线的等时距转换

图3中平移或异常点剔除后的还原曲线虽能得到路堑边坡水平位移总体趋势，但实际上还原后的数据序列并非等时距，存在因仪器故障或奇异点剔除产生的“漏点”现象。同时，还原后序列时间间隔基本保持为1.0 d，数据量过多，如果将序列时间间隔增大，在保证新序列总体趋势同还原后序列相似的同时，应用含有较少元素的新序列预测路堑边坡总体变形趋势或建立相应的预测分析模型，无疑更具有工程实用价值。

常用的等时距序列转换方法为插值方法，经典插值方法包括拉格朗日插值，牛顿插值，艾尔米特插值、分段线性插值及样条插值等[2]。这些方法均具有成熟的理论背景和丰富的工程应用经验。其中，拉格朗日方法具有结构简单，适用性广的优点，在数据点足够情况下，可实现任意多次的多项式插值。对应的，线性和二次抛物形式的拉格朗日基本插值公式分别如式(1)和式(2)所示。

(1)

(2)

式中，Xi为线性或二次抛物插值目标函数；(ti-1，xi-1)、(ti，xi)、(ti+1，xi+1)为原始序列数据点，且i>1;T为待插数据点对应的新时间序列。

图4为原始序列xi转换为等时距序列Xi的插值过程示意，根据图示过程，首先确定插值后的等时距序列时间间隔ΔT，其确定方法可预设一合理值，也可取原始时间序列各时间间隔的平均值，或者取原始时间序列的最小公约数。得到等时距序列时间间隔后，由式(3)确定插值后等时距序列的时间序列Ti，并依次赋值给时间T，应用式(1)线性插值或式(2)二次抛物插值得到最终的等时距序列Xi。

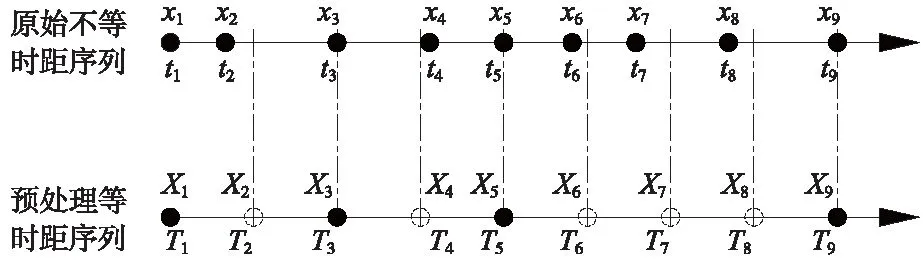
图4　等时距序列插值示意

式中，Ti为等时距时间序列；ΔT为等时距序列的时间间隔；t1为原始序列的第一个时间数据点。

特别的，应用拉格朗日插值公式进行插值计算中，当插值点附近还原序列相邻数据点的时间间隔比值小于2.0时，宜采用二次抛物插值方法；否则，应采用线性插值方法进行等时距序列转换。

通过上述方式，对图3中DCX1-2-2、DCX2-1-2和DCX4-2-2测点水平位移还原曲线进行等时距处理转换，得到包含由50个数据点组成的等时距序列，转换后等时距序列时间间隔约为13.2 d，各测点对应的等时距序列曲线如图5所示。

图5　三测点等时距序列曲线

对比图3(a)(b)(c)中三测点的还原曲线，包含50个数据点的图5等时距序列曲线能够反映出三测点水平位移时程曲线的变化趋势。400 d时间范围内，路堑边坡水平位移时程曲线基本保持线性增加趋势，但超过400 d后，路堑边坡变形趋于稳定。

此外，图5中插值后的等时距序列曲线中间数据仍表现出较强的波动性和随机性特点，研究中采用平滑降噪方法进一步处理，得到更为真实的路堑边坡位移变形趋势，以满足后续的位移预测模型建模和路堑边坡稳定性分析。

4　数据序列平滑与平滑效果评价

4.1　平滑降噪方法

一般情况下，边坡位移监测位移时程曲线大多呈现出明显的随机波动性特点，而其原因主要有两个方面，一是自然因素(降雨、地震、地下水变化等)和人为因素(施工、爆破、车辆振动等)等外部因素引起的，二是监测仪器本身由于磁场干涉、电压失稳等因素引起的监测信号周期性波动现象。而在位移发展趋势判定及位移发展预测模型建立中，应尽量去除随机性因素影响。因此，采用降噪方法对监测数据进行合理平滑去噪处理，保证降噪后数据不仅有效去除数据中的随机噪声数据部分，并且保留反映边坡总体变形趋势的有效数据信息。

目前，波动数据降噪处理已有多种方法，其中较为广泛使用的是最小二乘多项式平滑方法、傅里叶变换平滑、分箱技术及小波变换去噪技术等[2]。考虑到各方法实际工程应用效果和推广意义，本文在路堑边坡位移监测数据平滑降噪处理中采用最小二乘多项式平滑降噪方法，通过相对简单有效的途径，实现对边坡位移原始监测数据的高效快速处理。

设一组含噪声数据序列为X1，X2，…，Xn,,对应时间节点序列为T1，T2，…，Tn，应用m次多项式拟合数据，其拟合表达式为

Y(T)=A0+A1T+A2T2+…+AmTm

(4)

应用最小二乘法确定式(4)中方程待定系数，得到拟合关系式和目标数据间方差表达式(5)。

(5)

最小二乘法求解应使式(5)数值最小，分别对Xi(i=0，1，…，m)求偏导，并令各偏导数方程为0，得到式(6)形式的正规方程组。

(6)

由式(6)依次解得拟合方程系数A1，A2，…，Am。等时距序列平滑过程中，若平滑窗口采用五点数据格式，令时间序列为1，2，3，4，5，分别得到式(7)二次抛物线和式(8)三次抛物线五点平滑公式，式中，i=3，4，…，n-2。

(7)

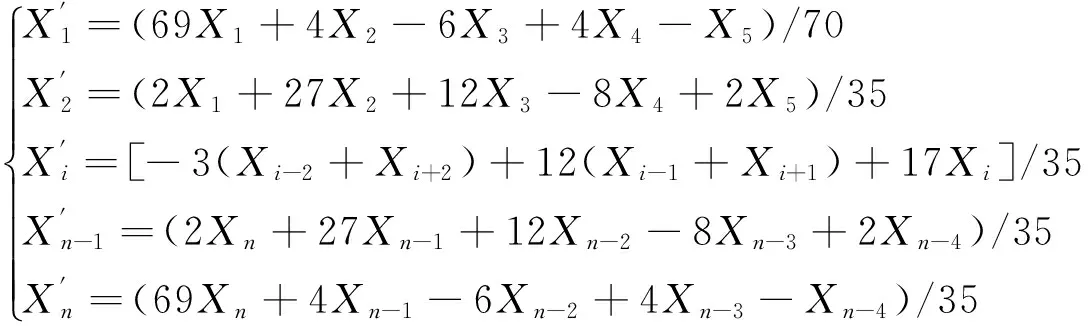
(8)

此外，应用比较多的还有三点平滑法，其实际上是一种取算术平均值的数学方法。考虑到边坡监测位移序列数据点较多，本文选用三次抛物线平滑方法进行插值完成后等时距位移序列的降噪处理。

平滑效果主要有均方根误差RMSE、信噪比SNR和平滑度指标r。各平滑效果指标表达式依次为式(9)、式(10)和式(11)形式。

(9)

(10)

(11)

均方根误差RMSE体现了原始数据与去噪后数据间的差异，均方差越小，表示去噪结果越接近原始序列；信噪比SNR是原始数据能量和噪声数据能量的比值，信噪比越大，降噪后序列同原始序列越接近，噪声水平越低；平滑度指标r反映出降噪后序列的相对平滑性能，平滑度指标越小，去噪效果越好。

4.2　断面测点水平位移还原曲线的降噪处理

数据序列降噪效果主要同循环次数相关，循环次数越多，降噪后的平滑序列噪声水平相对越低，平滑性也越好，但与原始序列间差异也越大。因此，原始监测数据平滑降噪处理过程中，应合理控制平滑循环次数，在保证处理后数列平滑度的基础上，保证降噪后数据不至于失真。

图6　降噪效果评价指标同循环次数间关系曲线

对包含50个数据点的DCX1-2-2、DCX2-1-2和DCX4-2-2测点等时距序列平滑降噪处理，得到不同循环次数下的均方根误差RMSE、信噪比SNR和平滑度指标r同循环次数N之间的关系曲线，如图6所示。从图6可看出，含噪序列平滑过程中，均方根误差RMSE、信噪比SNR、平滑度指标r分别随循环次数N的增加而升高、降低和降低，即降噪循环次数越多，平滑后数据序列同原始序列间差异越大，降噪后的序列噪声水平越低，序列平滑性越好。但同时，平滑后序列相较于原序列可能存在数据失真现象，故降噪循环次数并非越多越好。

图6中，当循环次数较小时，3种降噪效果评价指标均随循环次数的增加出现大幅变化，但当循环次数超过一定次数后，3种降噪效果评价指标的变化趋势渐缓，且总体变化幅度很小。因此，可将各降噪评价指标随降噪循环次数的变化曲线中曲率最大点后的某一循环次数作为合理值，在满足含噪数据降噪效果的同时，保证降噪后数据序列能够反映原始序列趋势的真实性。

对比图6(a)(b)(c)中均方根误差RMSE、信噪比SNR和平滑度指标r趋势线，当循环次数达到10次时，各趋势线曲率最大，序列降噪效果最为明显；循环次数达到20次时，基本可保证降噪后序列的各评价指标趋稳。因此，路堑边坡监测数据降噪处理采用五点三次抛物方程降噪中，统一进行20次左右的降噪循环，满足降噪后路堑边坡监测数据的平滑性和真实性。图7为经过20次循环平滑降噪后，DCX1-2-2、DCX2-1-2和DCX4-2-2测点平滑降噪后的序列曲线，三测点降噪后曲线随机性数据点明显减少，平滑序列平顺度显著提高。

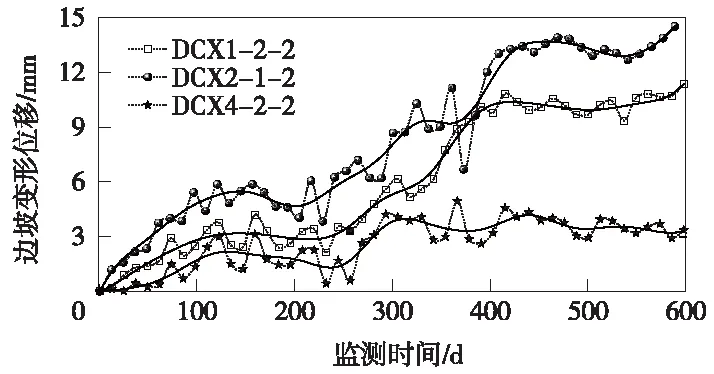
图7　20次循环后的三测点位移平滑降噪曲线

4.3　断面测点位移数据序列拟合方程

路堑边坡变形监测目的是进行边坡灾害预警和变形发展趋势预测，预警指标一般采用位移变形极限值或变形速率极限值，而变形趋势预测则需要根据路堑边坡监测位移时程曲线[13-15]。因此，20次平滑降噪处理后的边坡位移监测数据平滑曲线可通过多项式拟合方法，获得位移监测数据的拟合曲线，并进行边坡位移发展趋势的短期预测。

根据图7中DCX1-2-2、DCX2-1-2和DCX4-2-2三测点水平位移监测数据平滑降噪后的数据序列曲线，通过六次多项式拟合方法，分别得到图8中3个监测点平滑降噪后水平位移曲线的多项式拟合曲线。从图8可以看出，六次函数拟合曲线能够准确反映各测点水平位移随时间的变化趋势，说明应用高次多项式函数进行路堑边坡监测数据模拟是可行的。但必须说明的是，高次多项式函数并不能很好反映未来时间段内的数据序列变化趋势，仅能满足路堑边坡位移变形的短期预测，如果进行中长期预测则极可能产生较大预测误差。具体工程应用中，首先根据实测数据进行平移还原，平滑降噪处理后得到测点监测数据的还原曲线，并应用高次多项式函数拟合，最后进行未来短时间内的位移变形趋势和变形量预测。

图8　三测点位移多项式拟合曲线

式(12)为对应的六次多项式拟合方程式。表1为3个测点位移曲线的六次多项式拟合方程的各项系数列表，3个监测点高次函数拟合方程的相关系数均超过0.999 9，这也说明六次多项式函数拟合方法对已测位移变形数据具有较好拟合效果。

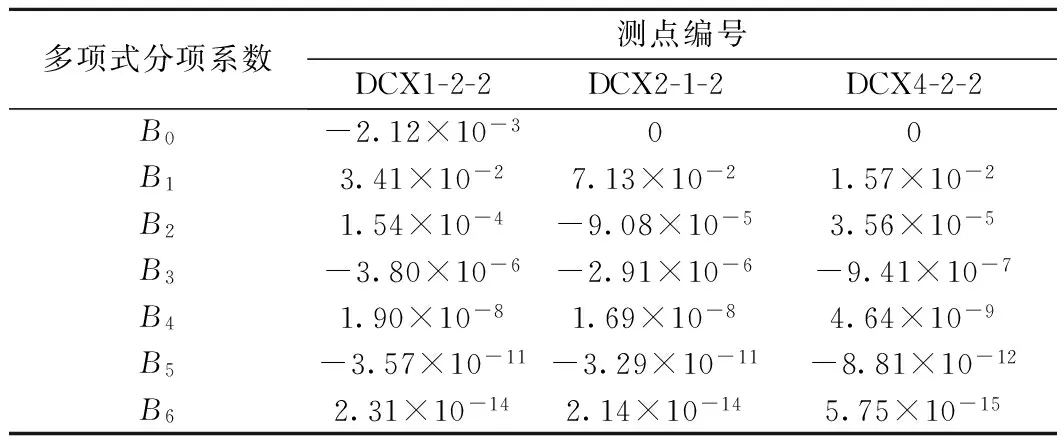
表1　试验段计算参数

X(t)=B0+B1t+B2t2+B3t3+B4t4+B5t5+B6t6

(12)

式中，X(t)为测点拟合位移；t为监测时间；B0～B6为六次多项式分项系数。

5　结论

路堑边坡位移监测直接反应开挖和运营过程中的边坡稳定状态和变形发展趋势，但由于众多因素的干扰影响，监测数据往往表现出较强的波动性和随机性，并不能代表边坡监测位移发展趋势，难以直接应用。研究中以长昆客运专线长沙至玉屏段部分路堑边坡水平位移监测结果为基础，开展原始监测数据的还原方法、等时距转换方法、平滑降噪方法和多项式拟合方法的研究，并得到以下结论。

(1)受制于现场诸多因素，路堑边坡自动监测数据时程曲线存在突变和波动现象，监测数据预处理中应根据曲线特点，采用平移或异常点剔除方法还原真实监测数据。

(2)测点监测数据序列等时距转换中，可采用线性插值或二次多项式插值，但当插值点附近相邻时间间隔比值超过2.0倍时，宜采用线性插值。

(3)还原后数据序列的平滑性随平滑循环次数逐渐增加，数据所含噪声水平逐渐降低；应用三次抛物线平滑方法循环降噪20次时，即可满足平滑降噪要求。

(4)平滑降噪后的等时距序列可应用高次函数多项式拟合，并能满足短期预测要求，但中长期预测效果较差，拟合数据范围应实时更新。

(5)该研究成果可为铁路工程路堑边坡自动监测数据的预处理方法提供参考和借鉴。

参考文献：

[1]唐元峰.长昆客运专线高瓦斯煤层地区隧址综合比选[J].高速铁路技术，2011(S1):357-361.

[2]蔚清.边坡监测数据预处理方法比较及建模研究[D].合肥：合肥工业大学，2013.

[3]张松，田林亚.时间序列分析在地铁沉降监测中的应用[J].测绘工程，2014，23(10)：63-66.

[4]陈善雄，余飞，刘绍波，等.铁路客运专线沉降监测数据管理与分析预测集成系统研发[J].铁道标准设计，2010(2)：31-36.

[5]郑怀洲.北京地铁东四站地表沉降监测数据分析[J].铁道标准设计，2006(4)：60-62.

[6]刘汉东，阮飞鹏，李国维.粤赣高速公路k2边坡监测与稳定性研究[J].岩土力学，2008，29(12)：3365-3369.