最小通信开销的Direct Send并行图像合成方法
2018-04-16杨平利黄少华林成地孔龙星
王 攀 杨平利 黄少华 林成地 孔龙星
(西北核技术研究所 西安 710024) (weaponfire2005@foxmail.com)
随着高性能计算技术的不断发展,科研工作者进行的数值计算规模不断扩大,数值模拟精度不断提高,所产生的数据量也随之不断增大.在大规模、高精度模拟条件下,所产生的数据规模常常达到TB级甚至PB级,对如此大规模的数据进行可视化处理已成为目前高性能计算领域的一个巨大难题.
并行数据可视化技术[1-3]是解决当前大规模科学数据后处理难题的重要手段之一,是科学可视化技术领域的研究热点.在如今模拟计算规模不断扩大的时代背景下,并行可视化技术越来越受到科研工作者的重视,目前已成为帮助科研人员探究大规模科学数据中隐含物理规律的有力工具.
按照绘制体系结构的不同,可将并行可视化技术划分为3类,即Sort-first,Sort-middle,Sort-last[4].其中Sort-last方法是唯一适用于大规模分布式集群的并行可视化方法.因此,目前针对大规模科学数据的并行可视化研究成果大多数均基于Sort-last方法[5].
Sort-last并行可视化流程可以分为3个主要阶段:1)将原始数据进行划分,分配到各个绘制节点;2)各个绘制节点独立绘制本地数据形成局部子图像;3)将各绘制节点的局部子图像进行全局合成,形成最终的结果图像.当绘制节点数较少时,由于单个节点所需绘制的数据量较大,因而绘制性能的瓶颈通常在于各个节点的数据处理及绘制阶段.然而随着节点数不断增加,单个节点所需绘制的数据量逐渐减少,图像合成阶段的并行通信开销将逐步增大,并行可视化的性能瓶颈将从单节点绘制阶段迁移至并行图像合成阶段,因而设计实现一种高效的并行图像合成方法对于提升大规模并行可视化的总体性能至关重要.
另一方面,在目前研究较多的原位可视化技术[6-7]当中,并行图像合成性能直接决定着原位可视化的总体性能,只有图像合成的时间开销足够小,才能够不影响到数值模拟计算,原位可视化技术才具有更好的实用价值.除此之外,高分辨率显示[8]也是大规模数据可视化的一项重要需求,更高的分辨率显示能够获得更多的数据细节,从而进一步加深科研人员对于科学数据的理解,而分辨率的提高必将导致并行图像合成开销的增加,因而研究高效的图像合成算法也是实现高分辨率实时显示的必然要求.
在大规模科学数据的并行可视化领域,现有的经典图像合成方法主要有Binary Swap[9],Direct Send[10],Radix-k[11],2-3 Swap[12]等方法.其中Direct Send方法是目前图像合成应用中使用最为广泛的一种方法,这不仅仅是因为Direct Send方法本身能够完成大规模并行绘制的图像合成,还在于Direct Send方法是其他图像合成算法的构建基础.例如,在Radix-k合成算法中,各个绘制节点被划分为若干组,而组内的多个节点则需要使用Direct Send方法实现图像合成.因而,Direct Send方法性能的优劣,将会直接影响到其他合成策略性能的好坏.
针对如何减少Direct Send方法中的合成通信量问题,本文提出一种指导图像子块并行合成的动态划分方法.该方法以统计各子图像中有效像素前缀和为基础,使用动态规划方法计算出最佳图像合成划分位置,使得按照该划分位置进行Direct Send图像合成时,合成通信开销最小.该方法改变了以往Direct Send方式按照均匀位置静态划分图像进行合成的方式,理论证明了本文方法能够使得通信计算量最小,并用实验验证了本文方法的有效性.
1 并行图像合成
1.1 并行图像合成方法
在大规模并行可视化情况下,以往最常用的并行图像合成方法包括Binary Swap[9],Radix-k[11],2-3 Swap[12]方法,其中Radix-k方法是一种更加通用方法,该方法可通过选择不同的k向量值,实现各种不同图像合成方式.
但上述3种方法存在共同的缺陷,即每一轮合成完毕之后都需要明确的通信同步操作,致使整体合成性能受到影响.文献[10]使用异步通信合成技术重新实现了Direct Send方法,实验表明:在小规模(节点数小于16)并行可视化情况下,异步通信的Direct Send方法性能优于Binary Swap算法,但由于Direct Send方法的通信复杂度在O(N2)量级,因而其并不适用于大规模并行可视化环境.最近,文献[13]借鉴了文献[10]中异步通信合成的思想,将Direct Send方法与树形合成方法结合,实现了一种基于TOD-tree结构的合成方法,实验表明,在大规模并行情况下,TOD-tree方法性能优于Binary Swap和Radix-k方法.
1.2 图像合成优化方法
在上述并行图像合成方法的基础上,可以进一步叠加诸多合成优化方法以减少通信开销,提高并行图像合成效率.这是因为在Sort-last绘制方法中,随着节点数目的增加,节点上分配的数据量将不断减少,因而单个节点绘制产生的图像将越来越稀疏,将稀疏图像进行压缩将获得很好的压缩比,从而降低合成通信开销,因此有必要设计实现高效的图像压缩方法,以有效减少通信开销,提高图像合成效率.
有效像素包围盒技术[14]是一种直观而高效的加速优化技术,使用简单的坐标轴平行包围盒即可快速剔除掉与合成无关的背景像素,节省网络传输带宽,但该方法的缺点是包围盒仅能划定绘制图像的最外层边界,在处理内部存在空洞或分布不连续的图像时,剔除背景像素的效率不高.
RLE(run-length encoding)方法[15-16]是一种常用的无损压缩方法,能够将有效像素序列进行统一的行程编码表示,完全去掉图像中的无效像素.虽然能够最大限度地去掉图像中的无效像素,但RLE方法的最大问题在于进行编码表示的计算非常耗时,这一缺陷也限制了RLE 编码方法在并行图像合成应用当中的使用范围.
ROI(region of interest)方法[17]是近年来提出的一种CPU与GPU协同实现的无效像素区域剔除方法,该方法采用探测最大无效像素空洞的方式,将原始图像分割为多个有效像素分布密集的子块,从而提高图像传输与合成的效率.虽然ROI方法的执行效率优于RLE方法,但是由于ROI方法是一个递归寻找无效像素空洞的过程,递归终止条件的选择对算法性能的影响很大,很难根据不同的具体应用给出一个统一的递归终止阈值,因此在算法执行效率以及无效像素剔除效果方面,ROI方法依然有待进一步改进.
针对RLE及ROI方法的不足,以往我们曾提出一种起始索引编码[18]的图像压缩方式,虽然性能优于RLE及ROI方法,但在实践使用当中发现,使用一维像素子向量方法对图像进行压缩存在局限,不能够很好地发挥二维图像的空间局部性,因而也存在进一步改进提升的空间.
2 最小化通信开销的Direct Send图像合成
2.1 Direct Send并行图像合成方法
Direct Send方法的合成步骤简单直观,每个绘制节点只需直接将某一图像子块发送到负责合成该图像子块的节点进行合成即可,定义不参与网络传输的图像子块为本位图像子块,则合成过程如图1所示.
图1中Pi j表示第i个节点的第j个图像子块,箭头指向表示数据传输方向.要使Direct Send图像合成过程中的像素传输开销最小,显然需要将具有最大有效像素数的图像子块作为本位图像子块,而传输有效像素数相对较小的图像子块.依照这一原则,文献[18]给出了一种近似最优的贪心算法(以下简称贪心算法),该算法首先将原始图像均匀划分成大小相等的若干图像子块,再从中挑选出满足图像合成条件的前N个具有最大有效像素数的图像子块作为本位图像子块,令剩余的N(N-1)幅图像子块传输到远程节点参与完成图像合成.

Fig. 1 Direct Send image composition on 4 nodes图1 Direct Send方法完成4个节点图像合成的过程
虽然贪心算法比经典Direct Send算法能够减少通信开销,但也存在2个方面缺陷:1)贪心算法本身并不能获得最优解,尤其针对不同的图像数据而言,使用贪心算法性能相比于最优性能的差异较大,难于控制与最优解的近似程度;2)该贪心算法的前提是图像子块源自于对原始图像的静态均匀切分,但显然不同的图像切分方法会导致有效像素数在图像子块中的不同分布,从而影响贪心算法的最优解或近似解的取值,因此要进一步缩小合成通信开销,必须改变静态均匀划分图像子块的合成策略.
由于图像子块切分位置的选择直接依赖于有效像素数的统计,因此下面首先给出基于二维像素块的无效像素剔除方法和有效像素前缀和计算过程,然后阐述如何利用有效像素前缀和列表计算最优图像子块划分方式,以使得合成通信开销最小.
2.2 基于二维像素块划分的无效像素剔除方法
文献[18]给出了一种基于起始位置索引编码GPU图像压缩方法,该方法使用一维结构的像素子向量提取并存储有效像素,但一维向量结构不能充分发挥图像的空间局部性,对无效像素剔除能力有限.
本文对文献[18]中的方法进行扩展改进,使用二维像素块代替原有的像素子向量结构,在原有压缩开销不变的情况下,进一步发挥了有效像素分布的空间局部性,有助于提升无效像素剔除率.同时在剔除计算过程中,生成了有效像素前缀和列表,为后续确定图像子块的切分位置提供了计算依据,整个计算流程如图2所示.

Fig. 2 Image compression based on 2D pixel blocks by GPU图2 GPU实现的基于二维像素块的无效像素剔除方法
图2给出了一个32像素图像的无效像素剔除过程,其中白色方块表示无效像素,灰色方块表示有效像素,启用8个GPU线程进行并行计算.下面简要描述图2中各步骤进行的主要操作:
步骤1. 将原始图像按照二维像素块进行划分(例如图2中每4个像素定义为一个二维像素块),并指定每一个GPU线程处理一个二维像素块,每个像素块大小为D(例如图2中D=4).
步骤2. 启动第i号GPU线程Ti(例如图2中有0≤i≤7,下同),扫描所分配的像素块Pi,若像素块中存在有效像素,则有效像素标志表(FA)的对应位置FA[i]写入1,否则写入0;再将像素块内的有效像素数写入有效像素计数表(SA)的相应位置SA[i].
步骤3. 计算SA和FA包容前缀和(inclusive prefix sum),生成有效像素数前缀和列表(PSA)以及有效像素标志前缀和列表(PFA);并令线程T0将列表PFA的末位值写入变量OAL中.
步骤4. 线程Ti判别FA[i]的值,若FA[i]=1,则将Pi的像素内容写入数组PA,将Pi的坐标位置写入数组OA,其中PA与OA的写入位置均为D×PFA[i];若FA[i]=0,则线程Ti执行结束.
上述步骤执行结束后,产生的数组PA,OA,OAL即为剔除无效像素后的原始图像表示,而数组列表PSA则将用于下一步的图像子块切分计算.
2.3 最小化合成通信开销
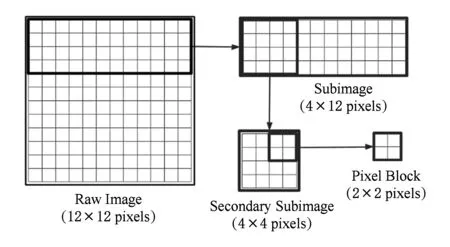
在经典Direct Send方法中,原始图像按固定位置被分割成均匀大小的图像子块,完成各图像子块的合成即完成图像合成过程.但是由于各图像子块的有效像素数目不同,因此采用均匀划分方式很难保证合成通信开销最小.本文将打破传统Direct Send方法中静态均匀划分图像子块的限制,提出一种动态图像子块划分方式,使合成通信开销最小.
假设有M个绘制节点使用Direct Send方式合成分辨率为N的图像,且每个节点的本地图像有效像素前缀和列表(PSA)已经计算完毕,那么最小化合成通信开销的图像子块分割问题可等价转化为如下问题:
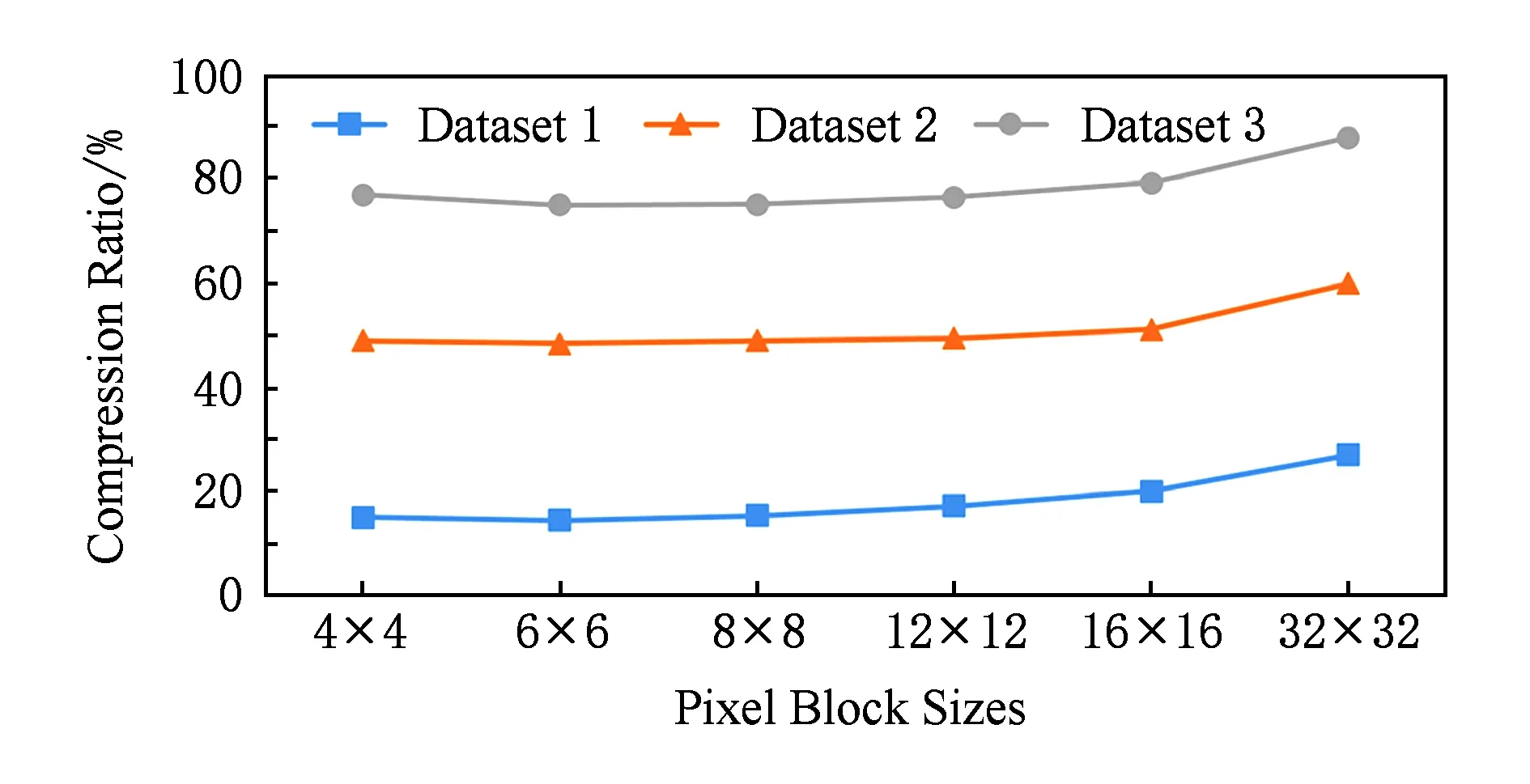
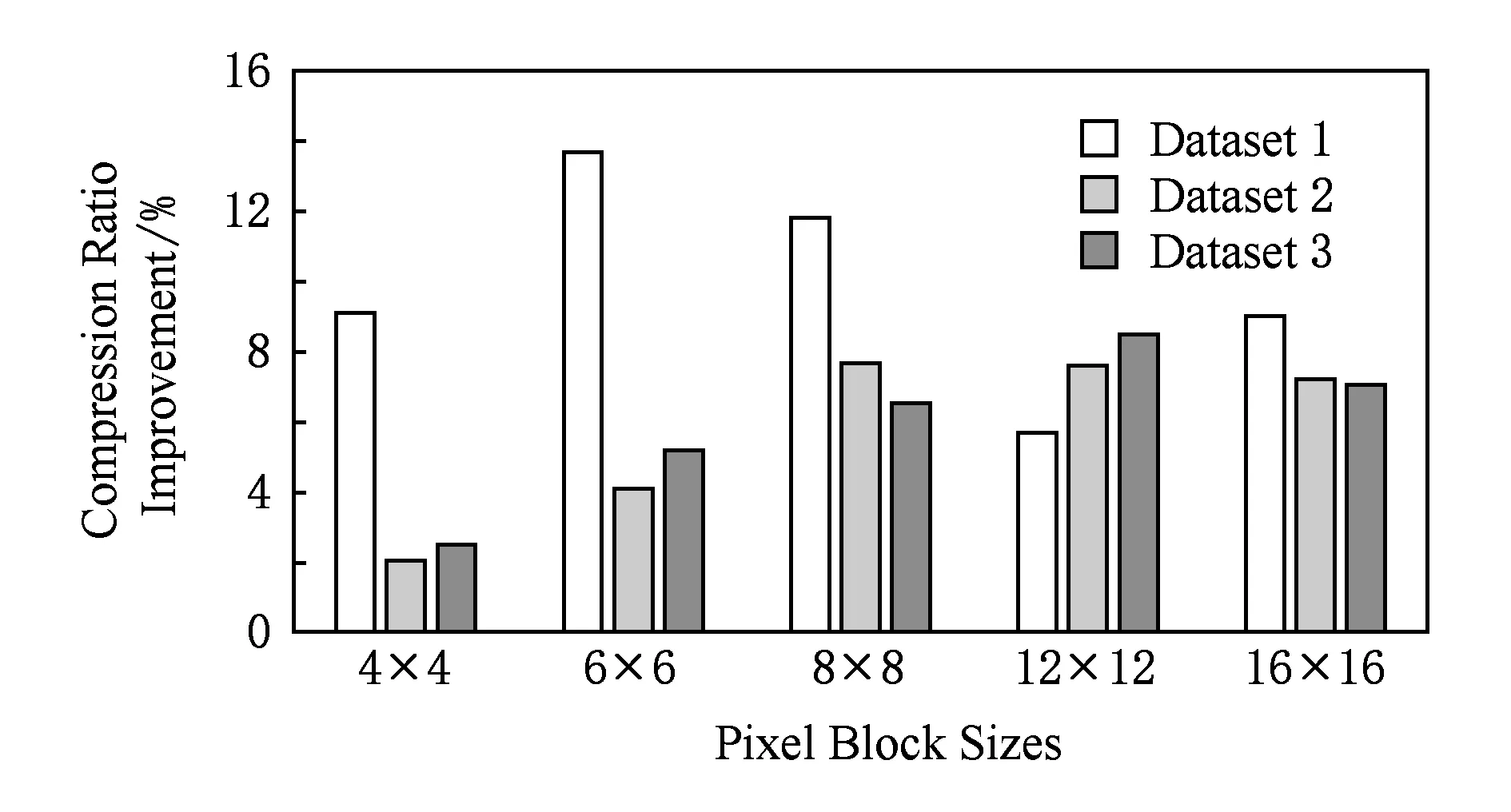
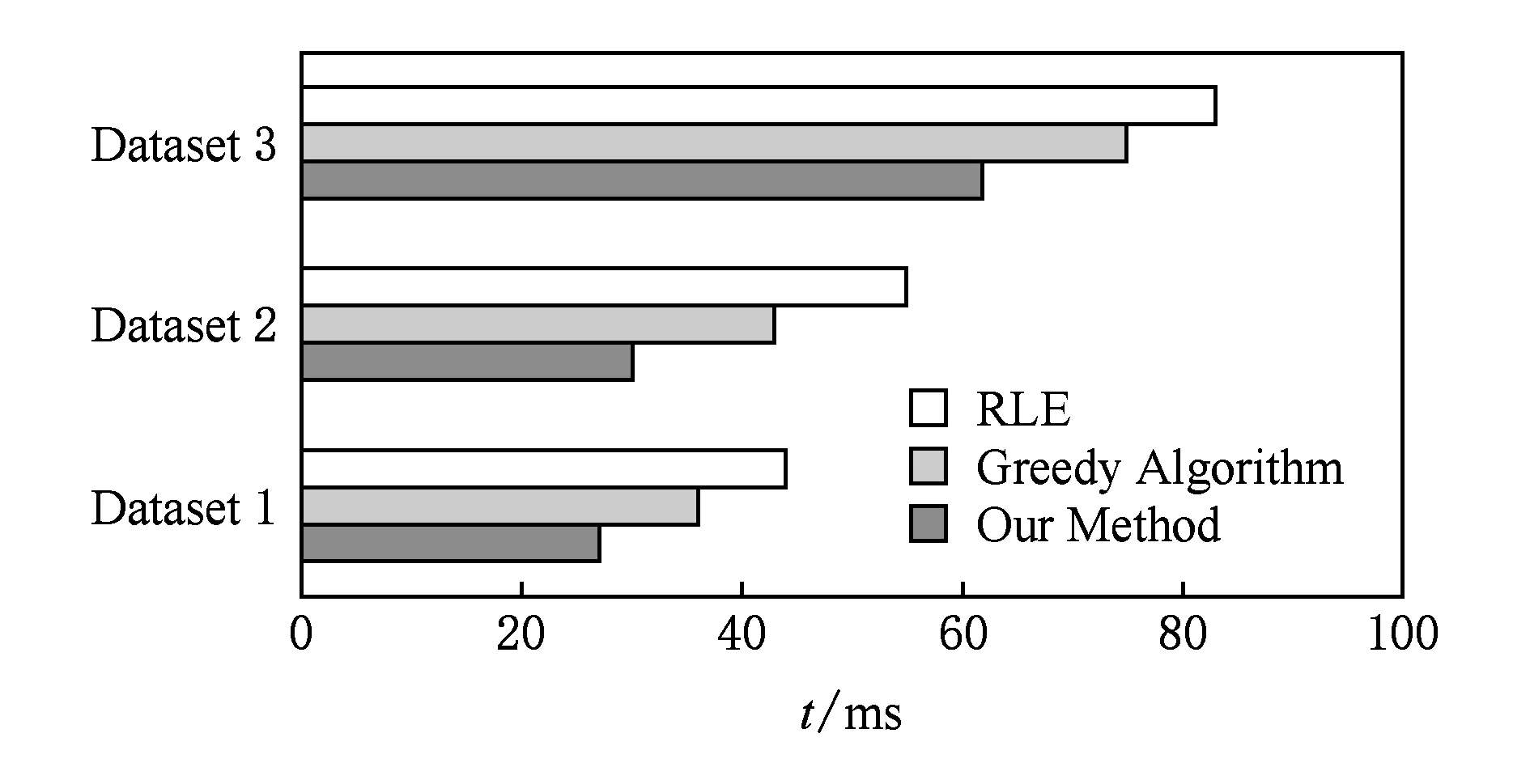
问题1. 假设有M个长度为N的前缀和向量组成的集合ψ={Ph|(1≤h≤M)},且已知Ph(1≤h≤M)的第k(1≤k≤N)个元素取值为Fh(k).要将集合ψ中的向量按照一致的分割位置E=(e1,e2,…,eM-1)切分成M段,如图3所示,其中向量E中的每一个元素为前缀和向量的位置下标(包含当前下标元素),且E中的元素满足0 (1) Fig. 3 The M prefix sum vectors are divided into M pieces. 图3 M个前缀和向量分成M段 问题1中前缀和向量集合ψ即对应各PSA组成的集合.之所以认为Q(E)取得最大值时合成通信开销最小,是基于准则:为了使合成通信开销尽量小,需要将有效像素数最大的图像子块作为本位图像保持不动,传输其他有效像素相对较少的图像子块进行图像合成. 因此当存在一种划分方式Ev使得Q(E)取到最大值时,令组成Q(Ev)的各个分段图像子块作为本位图像子块,传输其他图像子块进行合成,便能够达到通信开销最小,Q(Ev)即表示此时各个本位图像子块的有效像素数之和Qv,可将Qv表示为 (2) 其中Ω为划分序列集合,表示ψ上所有满足条件的划分序列E所组成的集合,显然Ev∈Ω. 分析可知,求取Ev的问题是一个典型的动态规划问题,因此定义价值函数w(i,j)表示从下标位置i(不包含i)到位置j(包含j)区段内,各前缀和向量的最大值,w(i,j)表达式为 (3) 定义函数g(n,m)为把前缀和向量前n列划分成m段所能够求得的本位有效像素数之和的最大值,由图像划分步骤可得递推公式: (4) 根据题目假设,显然有初始条件g(0,0)=0成立.由定义可知Qv=g(N,M),利用递推式(4)计算生成的k值序列即为划分序列Ev. 当图像分辨率N较大、绘制节点数M较多时,使用动态规范方法搜索最优解将是一个非常耗时的过程,为了满足实时绘制要求,在实践当中可以使用较大粒度的像素块数目N′代替像素数N,从而降低问题复杂度,在满足实时性要求的情况下求取近似最优解,实验部分将对这一求解方法做进一步讨论. 实验部分主要测试3个方面:1)将测试二维像素块大小对于压缩比率的影响;2)对动态规划计算开销展开测试;3)将本文算法与RLE算法及贪心算法进行性能对比,在不同绘制节点数目上实现Direct Send算法的图像合成,验证本文算法的有效性. 实验在一个16节点的GPU集群上展开测试,每一个绘制节点的配置如下:双路12核Intel Xeon E5 2697 v2 CPU,主频2.7 GHz;内存96 GB;配备Nvidia Quadro 5 000 GPU;Seagate 磁盘,容量3TB;1 Gbps以太网互联.选取3个不同放大比例的数值模拟数据作为测试数据,其中测试数据1和测试数据2是不同时间步电磁场PIC数值模拟的电场强度标量数据,网格维度均为750×750×1 000,测试数据3为激光等离子体PIC数值模拟的X方向电场标量数据,网格维度为500×500×800,使用KD-tree划分的Ray-casting方法进行体绘制可视化.绘制图像分辨率固定为4096×2048像素,通过选取不同的观察视点设置,统计得到测试数据1、测试数据2及测试数据3的有效像素数分别约占总像素数的13%,43%,71%(数据绘制结果如图4所示). Fig. 4 The Ray-casting rendering results of the testing datasets图4 测试数据的Ray-casting体绘制结果 由基于二维像素块的无效像素剔除过程可知,选择不同像素块大小,势必将对图像压缩性能造成一定影响,图5给出了不同像素块大小对于图像压缩比率大小的影响. Fig. 5 The compression ratios of testing images (compressed by 2D pixel block method)图5 二维像素块压缩方法的图像压缩比率 图5选取了6种不同大小的像素块做性能测试,在像素块小于16×16的情况下,像素块大小的选择对图像压缩比率影响效果并不明显,基本都能够获得较好的无效像素剔除效果,当像素块大小超过32×32时,压缩效果显著下降,因而像素块大小应选择在16×16以下为宜.从3个测试数据的综合压缩性能看,像素块为8×8的压缩比率较好,因而后面的实验测试均使用这一大小的像素块. 图6给出了本文方法与文献[18]中的一维子向量方法的压缩效果对比.从图5可以看出,使用二维像素块方法比一维子向量方法压缩比率有一定提升,在8×8像素块(一维子向量长度为64)的情况下,平均压缩比率性能提升在10%左右.因而在耗费相同计算开销的情况下,应当选择二维像素块方式对无效像素进行剔除. Fig. 6 The compression ratio improvement of 2D pixel block method compared with 1D vector method图6 二维像素块方法相对于一维子向量方法的压缩比率性能提升 如2.2节所述,若在原始前缀和列表的基础上,使用动态规划方法求解最优图像划分位置,所要搜索的解空间过于庞大,不可能满足图像实时显示的要求.因而,为了降低计算量,有必要将原始前缀和列表进行合并处理,使用一定粒度大小的图像次子块有效像素前缀和代替原始像素块的前缀和. 像素块、图像次子块、图像子块三者之间的关系如图7所示,其中一个图像次子块包含若干个像素块,而一个图像子块则包含若干个图像次子块. Fig. 7 The relationships among subimage, secondary subimage and pixel block图7 图像子块、图像次子块、像素块之间的关系 Fig. 8 The consuming time of dynamic programming in varying rendering nodes图8 不同节点数情况下动态规划求解的计算时间 图8中数据显示,当合成节点数较少时(如4节点情况),优化计算时间将会降到10-3s级,因此根据绘制节点数目选择适当的图像次子块个数,对于优化合成性能至关重要,目前还需要在实践过程中不断调整才能够获得较为满意的性能结果,这也是一个有待进一步研究探索的新问题. 另一方面,由于优化计算之前需要从各个节点收集各节点生成的前缀和列表,但由于动态规划的计算开销原因,仅需要收集若干个由像素块合并后的图像次子块前缀和列表,因而在现有高速网络带宽的情况下,前缀和列表的收集开销基本可以忽略不计. 本节将对本文提出的方法、贪心算法以及RLE编码方法做总体性能对比.本文方法使用8×8像素块对无效像素进行剔除,选取24个图像次子块前缀和进行动态规划计算. 在8绘制节点、16绘制节点情况下,3种方法的图像合成时间对比如图9、图10所示. Fig. 9 The composition time of the three methods on 8 nodes图9 在8个绘制节点上使用3种方法的合成时间对比 Fig. 10 The composition time of the three methods on 16 nodes图10 在16个绘制节点上使用3种方法的合成时间对比 由图9、图10可知,本文算法在不同绘制节点情况下,合成性能均优于贪心算法和RLE编码的传统Direct Send方法,因而进一步证明了使用最优分割点位置合成的Direct Send方法合成性能优于传统均匀分割图像方法. 实验中发现,使用本文方法在动态规划求解后,可能会出现单个绘制节点合成多幅图像子块的问题,这一点与传统Direct Send方法有所不同(传统Direct Send方法每个绘制节点仅指定合成一幅图像子块),正如文献[13]所述,在目前单个节点硬件配置条件下,合成负载不均衡所带来的合成性能影响远小于通信开销所带来的影响,由于实验中采用高性能GPU实现图像合成,因而实验中单个节点合成多幅图像子块并没有影响本文提出方法的有效性. 本文介绍了GPU上实现的基于二维像素块的有效像素剔除及前缀和计算过程;基于有效像素的前缀和列表,本文提出一种动态划分合成图像子块的方法,改进了现有Direct Send方法使用静态方式均匀划分图像子块的不足,降低了Direct Send合成通信开销,理论与实验均证明了本文方法的有效性. 限于硬件条件的限制,本文仅使用了16个节点的GPU集群做了实验测试,下一步将寻找更大规模的GPU集群做进一步的扩展性测试.对于如何依据合成节点数目选择图像次子块的数量,目前仍无统一的标准规律可循,有待于进一步探索研究.此外,目前使用的动态规划方法求解效率较低,研究该问题的并行求解方法,或者探索新的高效求解方法也是下一步研究的重点内容. 致谢感谢国防科技大学理学院卓红斌研究员提供实验测试数据! [1]Singh J P, Gupta A, Levoy M. Parallel visualization algorithms: Performance and architectural implications[J]. IEEE Computer, 1994, 27(7): 45-55 [2]Vo H T, Bronson J, Summa B, et al. Parallel visualization on large clusters using MapReduce[C]Proc of IEEE Large Data Analysis and Visualization (LDAV). Piscataway, NJ: IEEE, 2011: 81-88 [3]Shi Liu, Xiao Li, Cao Liqiang, et al. Two level parallel data read acceleration method for visualization in scientific computing[J]. Journal of Computer Research and Development, 2017, 54(4): 844-854 (in Chinese)(石刘, 肖丽, 曹立强, 等. 面向科学计算可视化的两级并行数据读取加速方法[J]. 计算机研究与发展, 2017, 54(4): 844-854) [4]Molnar S, Cox M, Ellsworth D, et al. A sorting classification of parallel rendering[J]. IEEE Computer Graphics and Applications, 1994, 14(4): 23-32 [5]Moreland K, Kendall W, Peterka T, et al. An image compositing solution at scale[C]Proc of 2011 Int Conf for High Performance Computing, Networking, Storage and Analysis. New York: ACM, 2011: 25-31 [6]Shan Guihua, Tian Dong, Xie Maojin, et al. In-situ visualization for peta-scale scientific computation[J]. Journal of Computer-Aided Design & Computer Graphics, 2013, 25(3): 286-293 (in Chinese)(单桂华, 田东, 谢茂金, 等. 千万亿次科学计算的原位可视化[J]. 计算机辅助设计与图形学学报, 2013, 25(3): 286-293) [7]Wang Fang, Li Sikun, Zhao Dan, et al. Advances in research and application of in-situ visualization[J]. Journal of System Simulation, 2015, 27(10): 2589-2599 (in Chinese)(王昉, 李思昆, 赵丹, 等. 原位可视化研究与应用进展[J]. 系统仿真学报, 2015, 27(10): 2589-2599) [8]Tao Ni, Schmidt G S, Staadt O G, et al. A survey of large high-resolution display technologies, techniques, and applications[C]Proc of 2006 IEEE Virtual Reality Conf. Piscataway, NJ: IEEE, 2006: 223-236 [9]Ma Kwanliu, Painter J S, Hansen C D, et al. Parallel volume rendering using binary swap compositing[J]. IEEE Computer Graphics and Applications, 1994, 14 (4): 59-68 [10]Eilemann S, Pajarola R. Direct send compositing for parallel sort-last rendering[C]Proc of the 7th Eurographics Conf on Parallel Graphics and Visualization. Aire-la-Ville, Switzerland: Eurographics Association, 2007: 29-36 [11]Peterka T, Goodell D, Ross R, et al. A configurable algorithm for parallel imagecompositing applications[C]Proc of High Performance Computing Networking, Storage and Analysis. New York: ACM, 2009: 1-10 [12]Yu Hongfeng, Wang Chaoli, Ma Kwanliu. Massively parallel volume rendering using 2-3 swap image compositing[C]Proc of High Performance Computing, Networking, Storage and Analysis. Piscataway, NJ: IEEE, 2008: 1-11 [13]Grosset A V P, Prasad M, Christensen C, et al. TOD-Tree: Task-overlapped direct send tree image compositing for hybrid MPI parallelism[C]Proc of the 15th Eurographics Symp on Parallel Graphics and Visualization. Aire-la-Ville, Switzerland: Eurographics Association, 2015: 67-76 [14]Takeuchi A, Ino F, Hagihara K. An improved binary-swap compositing for sort-last parallel rendering on distributed memory multiprocessors[J]. Parallel Computing, 2003, 29 (11): 1745-1762 [15]Ahrens J, Painter J. Efficient sort-last rendering using compression-based image compositing[C]Proc of the 2nd Eurographics Workshop on Parallel Graphics and Visualization. Aire-la-Ville, Switzerland: Eurographics Association, 1998: 145-151 [16]Moreland K, Wylie B, Pavlakos C. Sort-last parallel rendering for viewing extremely large data sets on tile displays[C]Proc of the 2001 IEEE Symp on Parallel and Large-Data Visualization and Graphics. Piscataway, NJ: IEEE, 2001: 85-92 [17]Makhinya M, Eilemann S, Pajarola R. Fast compositing for cluster-parallel rendering[C]Proc of Eurographics Symp on Parallel Graphics and Visualization. Aire-la-Ville, Switzerland: Eurographics Association, 2010: 111-120 [18]Wang Pan. Research on parallel visualization for large scale dataset[D]. Changsha: National University of Defense Technology, 2013 (in Chinese)(王攀. 大规模数据并行可视化关键技术研究[D]. 长沙: 国防科学技术大学, 2013) HuangShaohua, born in 1981. Assistant research fellow in Northwest Institute of Nuclear Technology. His main research interests include high performance visuali-zation, parallel computing and computer graphics. LinChengdi, born in 1986. Engineer of Northwest Institute of Nuclear Technology. His main research interests include visuali-zation in scientific computing and computer graphics.


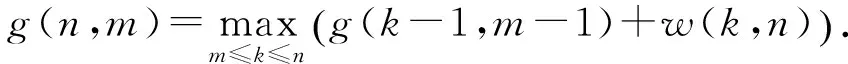
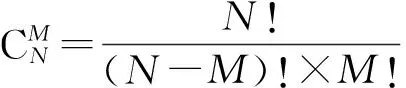
3 实验结果与分析

3.1 无效像素剔除测试
3.2 优化求解计算

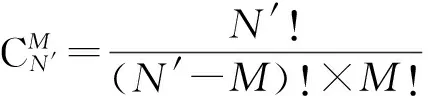
3.3 总体性能对比测试

4 结束语





