电场中的能量变化分析

2018-04-16

商品与质量 2018年39期

湖南冷水江市第一中学湖南冷水江 417500

电场本身是看不见、摸不着，存在于电荷及变化磁场周围空间里的一种特殊物质。在高中物理课程中学习电场相关知识时，往往是建立在人为的定义基础上的，因此电场相关知识很容易让高中学生感到抽象、困难。尤其是其中的能量变化相关内容，更是诸多学生学习过程中的一大难点。

1 电场中的力和能量

要想理解电场中的能量，首先需要充分理解电场的性质。通常来说，电场具有力和能量等客观属性，其中电场力的性质表现为电场对放入其中的电荷产生作用力，也就是所谓的电场力。而从能量的角度来看，如果电荷在电场之中移动，那么电场力会对电荷做功，也就是说电场具有能量。其中，电势能是指处于电场中的电荷分布所具有的势能，其大小、方向等与电荷的分布情况有关。实际上，电场中的能量变化，从某种程度上来说就是电场力做功与电势能相互转化的关系[1]。如果电场力做正功的话，电势能会转化成其它形式的能量；而电场力做负功的话，则是由其它形式的能量转化成电势能。

2 电场中的能量变化分析

电场中的能量变化，通常会涉及到电场力、重力、弹簧弹力、摩擦力等。根据所涉及力的类型不同，其能量变化情况也有所不同，需要根据实际情况进行合理分析。

2.1 电场中仅有电场力做功的能量变化

在仅有电场力做功的情况下，电场中的能量变化仅仅体现在带电粒子的动能及电势能的相互转化上，而且总能量不会发生变化。也就是说，仅有电场力做功会使电势能与动能之间进行转化，不会涉及到其它能量类型[2]。

已知某静电场的等势面如图1所示，其中各等势面间电势差大小一致，而且3的电势大小为零。那么某正电荷在只受静电力的情况下运动，其通过a点和b点时的动能大小分别是25ev与4ev。那么当该点电荷运动到某一位置且电势能大小为-8ev时，其动能为多少？

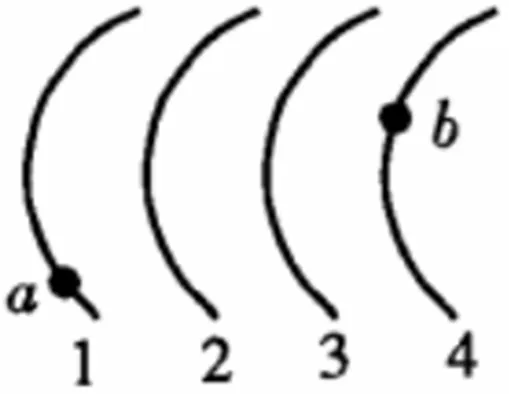
图1

解：由题意可知，正电荷仅受电场力作用，因此其运动过程中只会涉及到动能和电势能的转化，而且总能量保持不变。那么可以假设各等势面间电势差为U，因为等势面3的电势为零，那么可以得知等势面1的电势为-2U，而等势面4的电势为U。这时再假设正电荷的带电量为q，那么根据能量守恒可以得到正电荷在a、b两点时的能量关系，即-2qU+14=qU+4。计算，得到qU=7ev。假设正电荷到达c点时电势能大小为-8ev，那么根据能量守恒，可以得到正电荷在a、c两点时的能量关系，即：-2qU+25=-8+Ekc，计算得到Ekc=19ev。

2.2 电场中仅有电场力和重力做功的能量变化

如果电场中仅有电场力和重力做功，那么就涉及到动能、势能和电势能之间的相互转化，也就是机械能与电势能的转化和总能量不变。从某种程度上来说，这就是将常规的重力做功问题放在了电场之中，因此在解题时只需要从机械能和电势能两个角度进行思考即可。

如图2所示，某带电小球被细绳悬挂于匀强电场中，且该小球质量为m，带点量为q。如果将小球从悬线的竖直位置A处由静止加以释放，其会在到达B位置时拥有最大动能。假设小球运动过程中重力势能、电势能以及总势能的增量分别为ΔE1、ΔE2和ΔE3，那么请分别判断 ΔE1、ΔE2、ΔE3与 0 之间的关系。

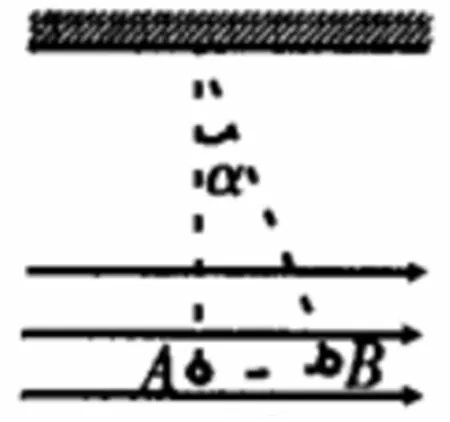
图2

解：由题意可知，带电小球在运动过程中仅受电场力和重力作用，因此其机械能和电势能之间进行相互转换，而且总能量守恒。由A点到B点，由于位置升高，小球的重力势能增加，因此ΔE1＞0。由于从A点到B点小球的重力势能和动能均有所增加，所以在能量守恒定律下，其电势能会减少，也就是ΔE2＜0。而从势能的角度来看，动能增加则意味着总势能必然会减少，故而ΔE3＜0。

2.3 电场中仅有电场力和摩擦力做功的能量变化

如果电场中仅有电场力和摩擦力做功，那么就会涉及到电势能、动能以及内能之间的相互转化，但是系统总能量维持不变[3]。

如图3所示，正电小物体在绝缘水平面上向右运动。已知其处于水平向左的匀强电场中，且在A点时动能为500J，在B电时动能为100J，其中减少的动能有60%被转化成电势能，那么当其再次到达B点时动能为多少？

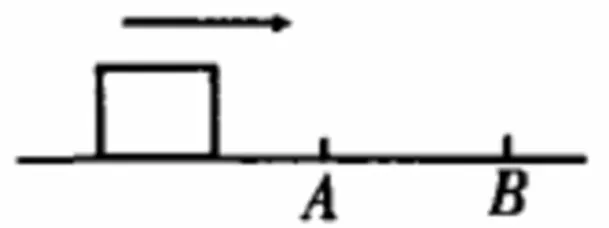
图3

解：由题可知小物体仅受恒定向左的电场力及与运动方向相反的摩擦力作用。由A点到B点，小物体的动能减少了400J，即动能为100J。减少的动能中60%被转化成了电势能，那么剩下的40%，也就是160J被转化成了内能。在小物体动能为零时，其依旧会有40%的能量用于克服摩擦做功而转化成内能，也就是100×40%=40J。之后小物体反向运动，那么当其到达B点时，同样需要克服摩擦力做功，且做工大大小与向右运动时一致，也就是40J。那么当小物体再次到达B点时，其电势能未发生变化，动能为100-40-40=20J