基于AHP和遗传算法的导弹作战任务分配问题研究

杨　晓　王玉玫

（华北计算技术研究所　北京　100083）

1　引言

导弹作战任务分配问题是进行作战任务规划的基础和前提。其目的是按照上级下达的作战命令或作战任务，为每个导弹部队分配攻击目标，选择适合的武器型号，使部队作战效能最高，并且作战代价最小。任务分配是任务规划中的重中之重，任务分配的方案将直接影响作战的效果。因此，研究任务分配问题，寻找最优分配方案，提高作战效能，仍是当前任务规划问题中的重要研究方向。

对于该问题，文献［1］描述了导弹作战任务分配流程，但是并没有提出具体解决方案；文献［2］使用并行的蚁群算法求解常规导弹作战任务分配，但是评价指标比较单一；文献［3］提出了基于作战能力的部队作战任务分配，并未具体说明部队如何量化部队作战能力；文献［4］主要解决的是航空突击作战中的任务分配问题，应用范围较小。现有研究都是阐述任务分配问题中的部队和导弹之间的匹配，忽视了目标的选择。实际导弹作战任务分配流程中，目标选择正确与否将直接影响作战的效果。因此本文综合考虑实际导弹作战流程，将目标优选考虑在任务分配过程中，并求解目标、部队以及导弹之间最佳匹配方案。

由此可见，任务分配的实质就是获取目标、部队以及导弹之间的最优匹配方案的过程。为了科学地实现导弹作战任务分配，本文将整个分配过程分为两步：先求得打击目标的相对重要权重，再确定部队打击最优方案。综合考虑目标在作战中的地位、经济价值及打击目标的紧迫性和可行性等因素，使用层次分析法［5］确定目标的重要程度。在此基础上，以多目标优化问题［6］描述任务分配，将目标毁伤效能最大与部队耗弹量最小作为优化的目标，最后通过遗传算法［7～9］得到最优分配方案。

2　层次分析法实现目标优选

2.1　目标优选考虑的因素

在实际作战中，影响目标价值的的因素有很多。综合参考多个文献和实际应用中的目标优选，影响目标价值的因素主要有：

1）目标地位

目标地位是指目标在作战中所起中的作用。主要包括三个方面：一是直接作战能力，目标在作战中所具有的火力点、拦阻能力等；二是指挥控制功能，目标在作战中的指挥、控制和通信能力；三是支援作战能力，目标在作战中能够提供经济和后勤物资保障的能力。

2）目标价值

目标价值是目标本身已有的价值，主要包括三个方面：经济价值、军事价值和政治价值。本文新提出考虑目标的军事价值和政治价值，在实际作战中，目标的军事价值和政治价值非常重要。

3）打击可行性

打击可行性是指对当前目标进行打击是否可行，主要包括目标易损性和打击该目标的效能。目标易损性是指目标受到攻击时是否容易损坏的一种特性。打击该目标的效能指我军对该目标的射击效能。

4）紧迫性

紧迫性是指打击当前目标的紧迫程度，主要包括对我军的威胁程度，即对我军实施火力攻击的可能性。

2.2　层次分析法实现目标优选

层次分析法［10］（Analysis Hierarchy Processing，AHP），是一种多准则决策方法。AHP求解决策问题时，将综合评价问题的各因素进行层次分解，建立目标综合评价层次结构；然后再两两比较每一层中的各元素，确定各元素相对重要权重；最后计算组合权重，获得各方案的相对重要性排序。层次分析法实现目标优选的具体流程如下：

1）建立目标综合评价层次结构

根据目标优选考虑的因素，将目标综合评价体系分为四层：目标层、准则层、指标层、方案层。目标层，即对目标重要性进行综合评价；准则层，即影响目标重要性综合评价的四个因素；指标层，影响目标重要性综合评价的各个指标；方案层，即待评价的目标。具体层次结构模型如图1所示。

图1　目标综合评价层次模型

2）确定各层元素的相对重要权重

建立目标综合评价层次结构后，就已明确了评价目标的因素与目标之间的关系。层次分析法将对各方案的综合评价分解为多层次的相对重要权重确定问题。基本原则是以上一层的元素为准则，确定该元素所支配的下一层各元素的相对重要性权重。

（1）构造判断矩阵

两两比较每层两元素，构造判断矩阵。由于对两元素进行相对重要性比较时，比较结果具有主观性，精确量化比较困难。因此，在实际操作时，将相对重要性划分为不同等级，根据重要性等级量化为一定数值。通常采用1～9标度法，将两元素相对重要程度量化，其标度含义如表1所示。

表1　1～9标度的含义

假定有n个元素 A1，A2，…，An，它们的相对重要性权重为 w1，w2，…，wn，将它们进行两两比较，以两元素的权重比值作为比较值即相对权重，可得n×n矩阵：

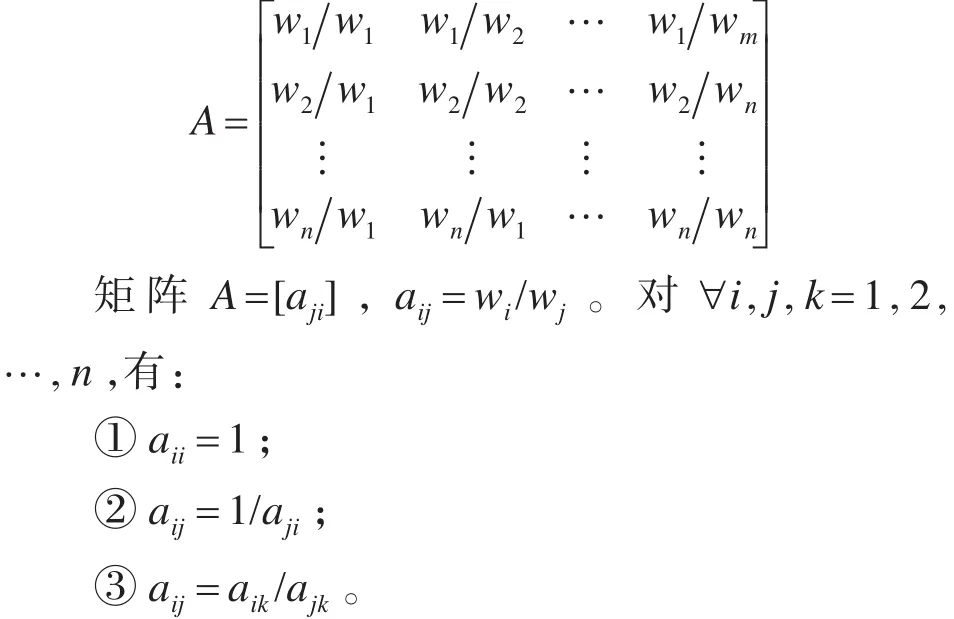
在数学上可以证明，具有上述特点的矩阵A具有唯一的非零最大特征值λmax=n。记权重向量W=(w1，w2，…，wn)T，而且容易验证：

因此，矩阵A的最大特征值n对应的特征向量即为权重向量W。

以上即是通过构造判断矩阵法来获得权重向量W的数学依据。即对各元素进行两两比较，来建立判断矩阵A，并求出A的最大特征值所对应的特征向量，作为各元素重要性的权重向量。

（2）判断矩阵一致性校验

为避免判断矩阵不一致性偏差太大，需要进行检验和修正。

检验判断矩阵一致性指标如下

CI值越大，说明构造出的判断矩阵与理想情况的偏差也就越大，其一致性越差。

当一致性指标CI＜0.1时，则认为判断矩阵的一致性比较好，否则需要对判断矩阵的取值进行调整。此时，引入维数修正值RI，当修正后的一致性指标CR=CI/RI＜0.1时，则认为满足一致性要求。其中，RI的值由表2给出。

表2　不同维数的RI值

（3）单元权重计算

在获得具有满意一致性的判断矩阵之后，上层元素所支配的各元素间的重要性权重就可以由判断矩阵最大特征值所对应的特征向量来表示。

2.3　计算组合权重

1）层次权重矩阵

规定层次模型中目标层的层次序号为1，层次序号从目标层至方案层递增。假定第i层有m个元素，第（i+1）层有n个元素，第（i+1）层各元素对第i层各元素的权重向量分别为…，，均为1×n的列向量。记L(i)=…，n×m，称为第i层的层次权重矩阵。

2）组合权重计算

得到各层次权重矩阵后，采用层次递推的方式计算各方案的组合权重。

第K层各元素即各方案对总目标的组合权重向量就是层次模型中各层次权重矩阵的乘积：

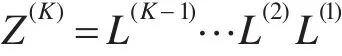
向量Z(K)的mK个分量的值就表示了相应方案对综合评价目标的重要性大小。

3　多目标优化求解任务分配

3.1　多目标优化问题概述

作战任务分配［11～15］是一个涉及多种资源合理分配的复杂的规划问题，本文采用多目标优化方法解决此问题。多目标优化问题，就是求得多于一个的目标函数在多约束条件下的最优解。

一般来说，多目标优化问题是由一组目标函数和若干约束条件构成，数学上的描述如下：

式中x表示解向量，y表示目标向量，X表示解向量x形成的解空间，Y表示目标向量y形成的目标空间，式（1）的约束条件确定解向量的可行取值范围。

多目标优化问题可以通过遗传算法求得最优解。首先采取权系数法将多目标优化问题转换为单目标优化问题，方便求最优解。对于一个多目标优化问题，如果为它的各个子目标函数 fi(x)(i=1，2，…，M)赋予不同的固定的权系数值ωi(x)(i=1，2，…，M)，其中 ωi满足：0≤ωi≤1(i=1，2，…，M)且ωi=1，各ωi的值表示对应子目标函数fi(x)在多目标优化问题中所占的重要程度。则各子目标函数的线性加权和即为

则多目标优化问题便转换为单目标优化问题，然后通过遗传算法求得最优解。

3.2　任务分配问题描述

本文考虑的导弹作战任务分配的目标函数是尽可能的使目标的毁伤效能达到最大，同时使部队导弹的使用量最少。其中，毁伤效能指标用毁伤目标数目的数学期望来描述。一般来说，一定数量的第i种导弹打击第j个目标的毁伤概率［10］可用下式表示：

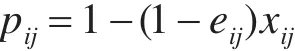
因此，m种导弹打击第j个目标的毁伤概率 pj为

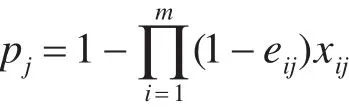
毁伤目标数的期望M为

综上，本文求解导弹作战任务分配问题的、目的有两个，一是使目标的毁伤效能指标达到最大；二是对导弹的使用量最小。所以，最优化的目标函

4　导弹作战任务分配问题实例

假设3个部队打击4个目标，相应的每个部队配有不同类型的导弹，其中部队T1配备导弹D1且至多具有8个单位，部队T2配备导弹D2且至多具有12个单位，部队T3配备导弹D3且至多具有15个单位。求使目标毁伤效能达到最大并且导弹使用量最小的导弹作战任务分配方案。其中不同导弹型号打击各目标的毁伤概率分别如表3和所示。

表3　导弹毁伤概率

1）通过改进的层次分析法求得目标重要程度

（1）建立目标重要性综合评价的层次模型

为简单起见，基于上面层次分析法介绍，建立如下所示的包含3层的目标重要性评价层次模型。

图2　目标重要性评价层次模型

（2）单元权重确定

①传染病可疑症状整合不足，疾病早期甄别能力有限。我国目前的症状监测一方面依托发热门诊为主进行流感样病例监测［9］，另一方面是以肠道门诊为主的感染性腹泻症状监测［9-10］，但仍缺乏针对皮疹、出血、黄疸、结膜出血等症状的监测，对传染病可疑症状的系统整合以及疾病早期的甄别能力存在不足。

根据目标重要性评价层次模型，建立第一层对对第二层各判断指标的判断矩阵，使用1～9标度法赋予相应数值，建立A-B判断矩阵，如表4所示。

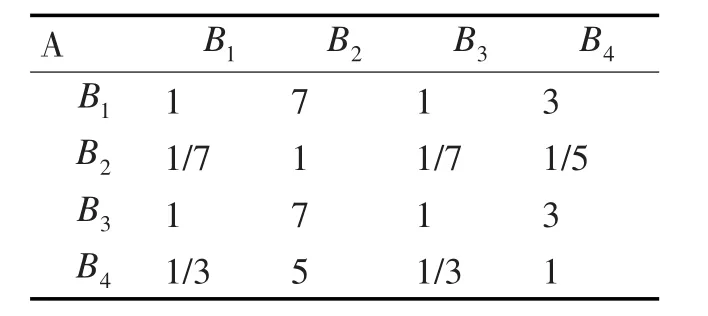
表4　A-B判断矩阵

求得A-B判断矩阵的最大特征值 λmax=4.0735，且最大特征值所对应的特征向量为［0.3950，0.0473，0.3950，0.1626］T。

进行一致性检验：

因此，A-B判断矩阵的一致性满足要求。所以，四个判断指标的相对重要性权值为：目标地位0.3950；经济价值 0.0473；紧急性 0.3950；可行性0.1626。

同样的方法求第二层中各评价元素对第三层各目标的判断矩阵，分别如表5～表8所示。

目标地位对各目标的判断矩阵如表5所示。

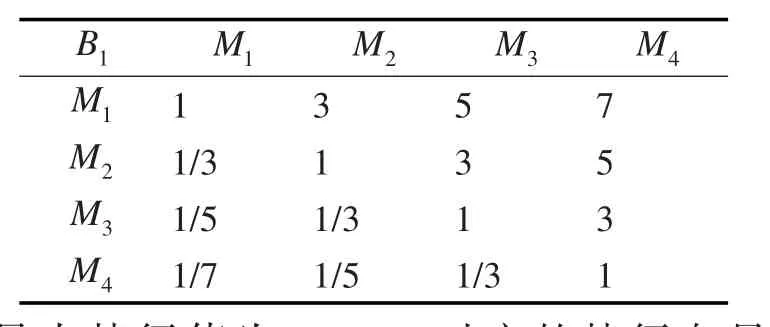
表5　目标地位对各目标的判断矩阵

最大特征值为4.1170，对应的特征向量为：［0.5650，0.2622，0.1175，0.0553］T。进行一致性检验：

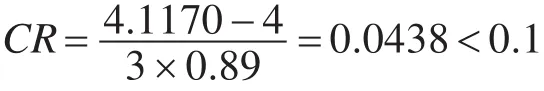
经济价值对各目标的判断矩阵如表6所示。

表6　经济价值对各目标的判断矩阵

最大特征值为4.1341，对应的特征向量为：［0.0913，0.0646，0.1910，0.6530］T。进行一致性检验：

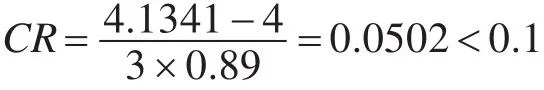
紧迫性对各目标的判断矩阵如表7所示。

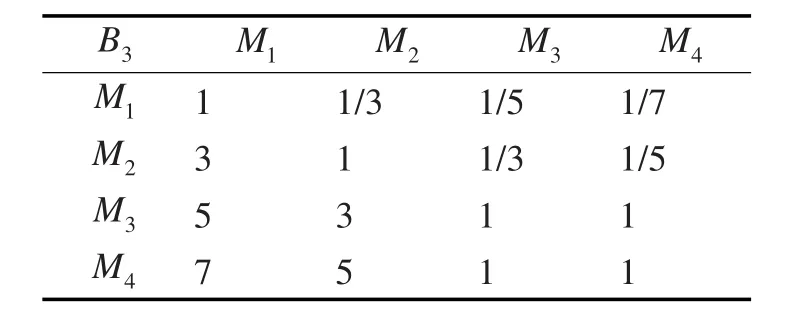
表7　紧迫性对各目标的判断矩阵

最大特征值为4.0820，对应的特征向量为：［0.0581，0.1253，0.3633，0.4532］T。进行一致性检验：

可行性对各目标的判断矩阵如表8所示。

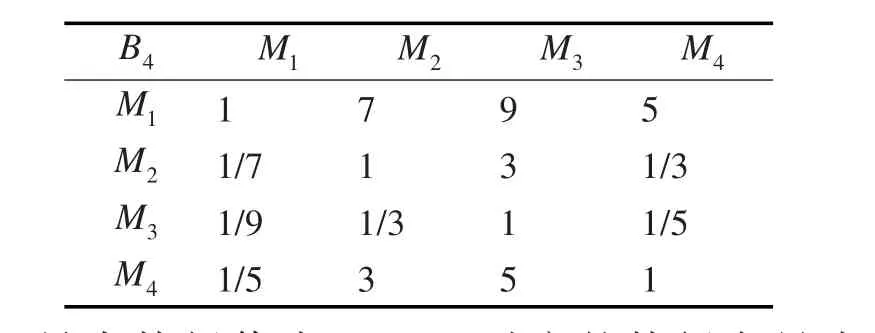
表8　可行性对各目标的判断矩阵

最大特征值为4.1707，对应的特征向量为：［0.6574，0.0942，0.0457，0.2027］T。进行一致性检验：

（3）组合权重计算

根据求解的单元权重结果，第一层和第二层的层次权重矩阵分别为：

各目标的重要性组合权重为

Z(3)=L(2)L(1)=[0.3573，0.1714，0.2064，0.2647]T

因此，各目标的相对权重为：M1:0.3573；M2:0.1714；M3:0.2064；M4:0.2647。

2）确定分配方案

设xij为第i（i=1，2，3）种导弹分配给第j（j=1，2，3，4）个目标的数量。最优化的目标函数为

使用遗传算法求解，经过计算，迭代400次求得上式的最优适应度值如图3所示。

对应图3的最优分配方案的结果如表9所示。

表9　最优分配方案

最优解为：部队T1使用导弹D1打击目标M1用2枚导弹，部队T1使用导弹D1打击目标M2用3枚导弹；部队T3使用导弹目标D3打击M3用3枚导弹；部队T1使用导弹D1打击目标M4用3枚导弹。

图3　最优适应度值

5　结语

常规导弹作战任务分配问题的研究具有很大的现实意义和军事应用价值。本文在分析导弹作战任务分配流程下，将任务分配问题分为了目标优选和任务分配。通过层次分析法分析计算各目标的重要程度，又通过多目标优化问题描述任务分配，通过遗传算法求得最优解。从实例来看，该方法能较好地完成任务分配。

［1］李淑媛.导弹作战任务分解分配问题［J］.火力与指挥控制，2010，35（4）：177-182.LIShuyuan.Missile CombatMission Decomposition Allocation Problem［J］.Fire Control and Command Control，2010，35（4）：177-182.

［2］杨颖，魏鹏，蒋鸣，等.基于并行蚁群算法的常规导弹作战任务分配［J］.弹箭与制导学报，2014，34（5）：189-192.YANG Ying，WEIPeng，JIANG Ming，et al.Conventional Missile Combat Task Assignment based on Parallel Ant Colony Algorithm［J］.Journalof Projectiles；Rockets；Missilesand Guidance，2014，34（5）：189-192.

［3］王正元，姬宏斌，屈娜，等.基于作战能力的部队作战任务分配方法［J］.指挥控制与仿真，2015，37（1）：15-18.WANG Zhengyuan，JIHongbin，QUNa，etal.CombatMission Assignment Method based on Combat Capability［J］.Command Controland Simulation，2015，37（1）：15-18.

［4］张磊，姚佩阳，徐雪洁，等.考虑任务可达约束的突击作战任务分配方法［J］.计算机工程，2012，38（24）：239-243.ZHANG Lei，YAO Peiyang，XU Xuejie，etal.Task Assignment Method For the Task Force that Considers the Constraints［J］.Computer Engineering，2012，38（24）：239-243.

［5］易图明，李杰，刘丽冰，等.基于层次分析法的炮兵作战目标优选研究与设计［C］//2014第二届中国指挥控制大会，2014：538-541.YITuming，LIJie，LIU Libing，etal.The Research and Design of Artillery Combat Target based on AHP［C］//The Second China Command and Control Conference，2014：538-541.

［6］肖晓伟，肖迪，林锦国，等.多目标优化问题的研究概述［J］.计算机应用研究，2011，28（3）：805-808.XIAO Xiaowei，XIAO Di，LIN Jinguo，et al.Research Overview of Multi-objective Optimization Problems［J］.Application Research of Computers，2011，28（3）：805-808.

［7］马晓姝.多目标优化的遗传算法研究［D］.西安：西安电子科技大学，2010.MA Xiaoshu.Research on Genetic Algorithm of Multi-objective Optimization［D］.Xi'an：Xidian University，2010.

［8］陈思，胡涛.基于多目标优化遗传算法的武器-目标分配［J］.舰船电子工程，2015，35（7）：54-57.CHEN Si，HU Tao.Weapon-target Assignment with Multi-objective Non-dominated Set Ranking Genetic Algorithm［J］.Ship Electronic Engineering，2015，35（7）：54-57.

［9］马永杰，云文霞.遗传算法研究进展［J］.计算机应用研究，2012，29（4）：1201-1206.MA Yongjie，YUNWenxia.Research Progress of Genetic Algorithm［J］.Application Research of Computers，2012，29（4）：1201-1206.

［10］陈琪锋，孟云鹤，陆宏伟.导弹作战应用［M］.北京：国防工业出版社，2014.CHEN Qifeng，MENG Yunhe，LU Hongwei.Missile combat application［M］.Beijing：National Defence Industrial Press，2014.

［11］寇英信，王琳，周中良.多目标攻击条件下的作战任务分配模型研究［J］.系统仿真学报，2008，20（16）：4408-4411.KOU Yingxin，WANG Lin，ZHOU Zhongliang.Study of Combat Task Allocation Model in Multi-target attack contion［J］.Journalof System Simulation，2008，20（16）：4408-4411.

［12］赵国宏，罗雪山.作战任务规划系统研究［J］.指挥与控制学报，2015，1（4）：391-394.ZHAO Guohong，LUO Xueshan.On Operation Mission Planning System［J］.Journal of Command and Control，2015，1（4）：391-394.

［13］杨萍，毕义明，肖海波，等.复杂约束下的导弹作战任务规划模型和算法研究［J］.指挥控制与仿真，2009，31（2）：14-17.YANG Ping，BIYiming，XIAO Haibo，etal.Research on Model and Algorithm of Missile Operational Mission Planning under Complex Constraints［J］.Command Control&Simulation，2009，31（2）：14-17.

［14］李赵阳.基于粒子群算法的武器-目标分配问题求解［D］.长春：吉林大学，2009.LI Zhaoyang.Weapon-target Assignment Problem Solving Based on Particle Swarm Optimization Algorithm［D］.Changchun：Jilin University，2009,

［15］王学文，王士坤，武世勇，等.基于毁伤能力的作战任务分配方法分析与建模［J］.火力与指挥控制，2014，39：66-70.WANG Xuewen，WANG Shikun，WU Shiyong，et al.An Analysis and Modeling of Operational Task Sharing Based on Damage Capability［J］.Fire Control and Command Control，2014，39：66-70.

［16］Qing Song，Ai，Zhou Liu，Yan Wang.Genetic Algorithm for the Multi-Objective Optimization of Product Gene［J］.Embedded and Multimedia Computing，2012：116-121.