分析三角函数恒等变形在物理解题中的应用

贾若菲

山东师范大学附属中学 山东济南 250000

在高中物理的学习过程中，我们经常会使用比较普遍的思维模式来解决问题，根据问题分析题意，然后根据题意寻找到解决方法，我们一般会使用画图法，将问题直观化、简单化。

1 激发学习物理的兴趣

俗话说兴趣是学生最好的老师，由此可以看出在学习的过程中，激发学生学习兴趣，有利于调动学习积极性，提高学习效率，加强对物理知识的学习[1]。在物理学习中，将数学三角函数恒等变形应用在物理解题中，可以激发学生的学习积极性，使学生在学习的过程中，积极探索，加强对物理知识的学习。通过激发学生的学习兴趣，能够促进学生对物理知识的掌握，进而提高解题能力。

例如，如图，一个小木块的质量为M，将其放在水平地面上，小木块与水平地面之间的摩擦系数为µ，若用最小的力移动木块，那么最小作用力是多少？

解析：在解决这一问题时，首先我们会想到利用公式N=mg,F=f=μmg来计算，但是，在实际解题过程中，我们应先分析物体受力情况。如图，根据物体受力情况可以得出：设，拉力F与地面水平夹角为θ，得到Fcosθ-f=0,N+Fsinθ-mg=0,根据这两个公式可以得出 F=µmg/（cosθ+µsinθ)；由此可见，当cosθ+µsinθ取最大值时，F=Fmin，这时可以发现，这并不是简单的物理问题，可以将其转化为数学问题进行计算，将cosθ+µsinθ三角函数和的形式转化成一个角的三角函数的形式求解，根据asinx+bcosx=√a2+b2sin(x+φ)tgφ=b/a，令 a=φ,b=1,则 可以得出：cosθ+µsinθ=√1+µ2sin（x+φ），根据上式可以得出：cosθ+µsinθ=√1+µ2sin（θ+artctgµ)。由于三角函数正弦函数的最大值是 1，所以，sin（θ+artctgµ)=1时，（θ+artctgµ)=90°，即θ=90°-artctgµ，由此可以推出拉力等于最小拉力，故最小作用力为 µmg/√1+µ2。

在解题过程中，其不仅涉及到了物理知识，而且还应用了数学中的三角函数知识，从而我们可以体会到学习的乐趣，有利于提高解题效率。

2 培养物理解题思路

在高中物理学习过程中，我们应用三角函数知识来解题，有利于形成正确的解题思路，拓展思维模式，提高思维能力[2]。在物理问题中应用三角函数知识进行解题，不仅能够使物理的解题效率得到提升，而且数学解题效率也会随之提高，久而久之我们将养成良好的思维模式，形成解题思路。

例如，一个运动员，在距离球门11m处的位置投球，为了将球从球门的横梁下边缘踢进球门，已知，球重0.25kg，横梁下边缘离地面高度2.5m（，不计空气阻力），那么运动员传给球最小动能是多少？

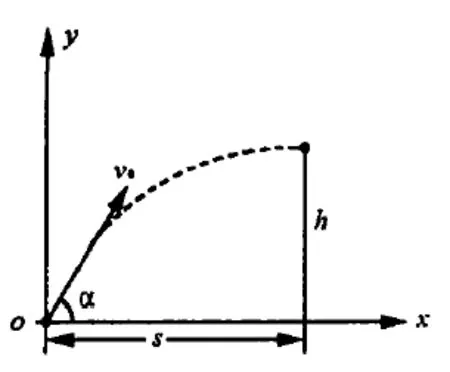
解析：如图，根据题意可以得知，球做斜抛运动，可以得出：s=v0cosα*t，h=v0sinα*t-1/2gt2，将两个公式结合，可以得出v02=gs2/(ssin2α-hcos2α-h)，若令 v02取最小值，则ssin2αhcos2α-h取最大值，则cosθ=s/√s2+h2,sinθ=s/√s2+h2,tg θ=h/s。ssin2α-hcos2α=√s2+h2sin(2α-θ)。因 此 sin(2αθ)=1.2α-θ=90°.可以得出α=（90°+arttgh/s）/2。

利用三角函数恒等变形的方式进行解题，学生的解题思路会更加清晰，学习效率也会随之提高，有利于学生的全面发展。

3 有利于物理知识学习

在高中物理的学习中有很多抽象的物理知识，学生在学习的过程中无法灵活地应用掌握计算技巧。将三角函数恒等变形应用在物理问题中，可以将复杂的问题简单化，提高解题质量。

例如，重量为G，半径为R的球体，放在竖直的墙和板AB之间，AB板可绕轴A自由转动,板的B端用绳固定,若板长为L,板与墙间的夹角为θ,忽略板重求：绳子的拉力T为多少。

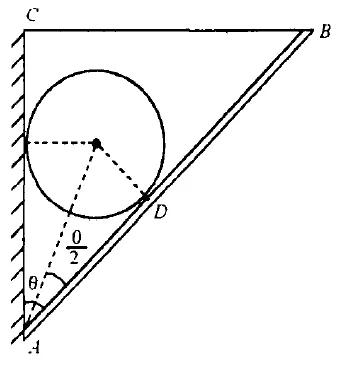
解析：根据题目可以得出，T=G/sinθ*{R/tg(θ/2)}/Lcosθ，由此可以得出N=N1=G/sinθ,∑MA=0，又AD=R/tgθ2,根据上式可以得出Tmin=4GR/L.

在高中物理问题中，应用三角函数恒等变形进行解题可以将复杂的问题简单化，降低学生学习难度，提高学习效率，有利于推动高中物理的发展。

总而言之，在高中物理教学中，应用三角函数恒等式变形进行教学，有利于激发学生的好奇心。将其应用在实际问题中，不仅可以拓展学生的解题思路，而且还能够激发学生的学习兴趣，有利于提高学习效率。