Modeling of single film bubble and numerical study of the plateau structure in foam system *
2018-04-13ZhongguoSun孙中国NiNi倪妮YijieSun孙一颉GuangXi席光
Zhong-guo Sun (孙中国), Ni Ni (倪妮) , Yi-jie Sun (孙一颉) , Guang Xi (席光)
Modeling of single film bubble and numerical study of the plateau structure in foam system*
Zhong-guo Sun (孙中国), Ni Ni (倪妮) , Yi-jie Sun (孙一颉) , Guang Xi (席光)
The single-film bubble has a special geometry with a certain amount of gas shrouded by a thin layer of liquid film under the surface tension force both on the inside and outside surfaces of the bubble. Based on the mesh-less moving particle semi-implicit (MPS) method, a single-film double-gas-liquid-interface surface tension (SDST) model is established for the single-film bubble, which characteristically has totally two gas-liquid interfaces on both sides of the film. Within this framework, the conventional surface free energy surface tension model is improved by using a higher order potential energy equation between particles, and the modification results in higher accuracy and better symmetry properties. The complex interface movement in the oscillation process of the single-film bubble is numerically captured, as well as typical flow phenomena and deformation characteristics of the liquid film. In addition, the basic behaviors of the coalescence and connection process between two and even three single-film bubbles are studied, and the cases with bubbles of different sizes are also included. Furthermore, the classic plateau structure in the foam system is reproduced and numerically proved to be in the steady state for multi-bubble connections.
Single film bubble, mesh-less moving particle semi-implicit (MPS), modeling, plateau structure
Introduction
The single film bubble is the basic unit of a foam, and it has a special structure and mechanical character- istics that a bulk of gas is enfolded by a very thin liquid film, withthe surface tension force both on the inside and the outside of the liquid film. It is quite common that one single bubble of this kind will stay in a sphere shape because of the pressure difference between the two sides and also the shrinking tendency from the surface tension force. In the case of two single film bubbles acting with each other, the coa- lescence or the connection would happen, respectively, under different conditions. When the coalescence happens, a new larger bubble would be generated, and the volume of the gas inside the new bubble is the summation of those in the two original bubbles. When the connection happens, a stable new interface between the two connected bubbles is generated, and the two original bubbles remain their presences with some deformation.
The gas-liquid interface and the action of the surface tension on the free surface have attracted many studies. In the theoretical analysis aspect, Chan et al.[1]proposed a two-stage model for bubble genera- tion. Yang et al.[2]analyzed the volume of the bubbles in the liquid based on the two-phase fluid dynamics theory, with an equation to calculate the bubble volume and estimate the size of the bubble.
In the experimental aspect, Zhang et al.[3]used the high speed camera to investigate the bubble move- ment in the water. Chan reviewed the studies of the film drainage process of the droplet and the bubble by using the atomic force microscope, the optical inter- ference stripe image and the coalescence timing. Gu et al.[4]used the double parallel probe and the camera to study the single bubble flow inside a horizontal straight tube.
In the numerical simulation aspect, the conven- tional CFD methods involve the Front-tracking[5], the VOF[6], the Level-set[7]and the LBM[8]and others. Chen et al.[9]employed the VOF method to investigate the influence of the surface tension coefficient and the viscosity coefficient on the rising bubble movement. Zhang and Wu.[10]used the interface reproducing technology in the VOF to discuss the interaction between the bubbles with different position settings in the liquid. Sussman combined the VOF and Level-set methods and simulated the bubble rising without viscosity and the sphere bubble breaking near the wall[11]. The LBM method[12, 13]was also applied in the researches concerning the deformation of a single bubble or several bubbles.
However, most studies focused on the bubble’s shape and deformations in the liquid or the tube based on the single-gas-liquid-interface surface tension model. The behavior of a single film bubble in the air, with double-gas-liquid-interfaces was not well studied, because high demands on the interface tracking and the computational stability in the numerical method are involved due to the double-interface structure and the very thin liquid film, and also due to the fact that the coalescence and connection process is always accompanied with a large deformation and a complex interface change.
The moving particle semi-implicit (MPS)[14]is employed in this study due to the advantage in dealing with the large deformation. So far, the MPS method was successfully used in engineering and science, such as the bubble rising and the deforming process in water[15], the free surface movement driven by the surface tension force[16-19]. This paper will study the coalescence and connection process for a single film bubble, and simulate the plateau structure by using improved models of the meshless MPS method.
1. Numerical method
The MPS method is a meshless method and is based on the same theory as the ISPH method but with a different equation solving process. In the MPS, the pressure field is calculated implicitly by solving a pressure Poisson equation. The skeleton of the method is as follows:
(1) Governing equations
The governing equations of the fluid mechanics include the conservation equations of the mass and the momentum. For an incompressible flow, they can be written in a Lagrangian form as:
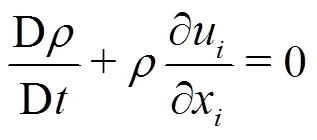
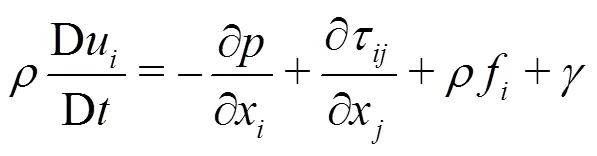
1.1 Kernel function
In the MPS method, the kernel function is used to form the particle action model to discretize the control equations:
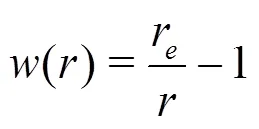
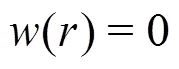
1.2 Gradient operator and laplacian operator
The gradient operator and the Laplacian operator in the control equation can be discretized based on the kernel function:


In the MPS method, these discretization operators are based on the kernel function as the model of interaction between particles.
2. Surface tension model
2.1 Basic thoery for single film bubbe

2.2 Surface tension model for single film bubble
Based on this theory, a single-film double-gas- liquid-interface surface tension model (SDST) for simulatingasinglefilmbubbleisproposed asshown in Fig. 2. Within the framework of the MPS method, the surface tension forces on the two interfaces willbe calculated integrally using the surface free energy surface tension model, which will be discussed later on.
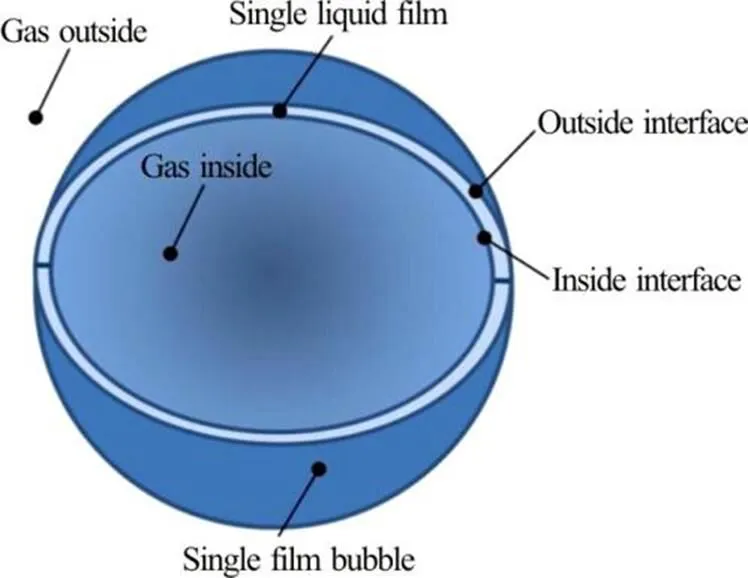
Fig. 1(Color online) The structure of single film bubble
The influence of the outside gas on the bubble will be totally ignored except as the atmosphere pressure, because the flow of the liquid film and the deformation of the bubble all happen in a very low Reynolds Number with a very small velocity. In the algorithm of the MPS, there will be no fluid particles in the gas phase outside the bubble, and on the outside free surface open in the air we have zero pressure constantly.
On the other hand, the gas inside the bubble is considered as incompressible with density and pressure. The incompressible viscosity fluid particles are assigned with physical parameters of a gas, and the pressure of these particles on the inside interface is set the same as that of the gas inside the bubble.
In order to accurately calculate the surface tension force on both sides, an interlayer of viscous fluid particles is employed to represent the liquid between the two interfaces, and their flow parameters such as the velocity, the position and the pressure are all as calculated.
2.3 Surface tension force calculation
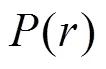
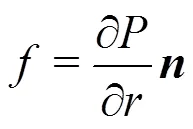
The force between the particles can be calculated by different formulas[21]. When the distance between the particles is less than the critical value, it is a repulsion between them; when the distance is greater than the critical value, it is attractive, a balance is achieved when it takes the critical value. For the particles with particles of uniform and symmetrical distribution around, the resultant force on them is 0, when the particles are on or adjacent to the free surface, the resultant force is not 0, that is the surface tension.
For the force between particles, their different densities (liquid and gas particles) are considered but not shown in this basic SFE model study. Therefore, the formula for calculating the potential energy between particles is:


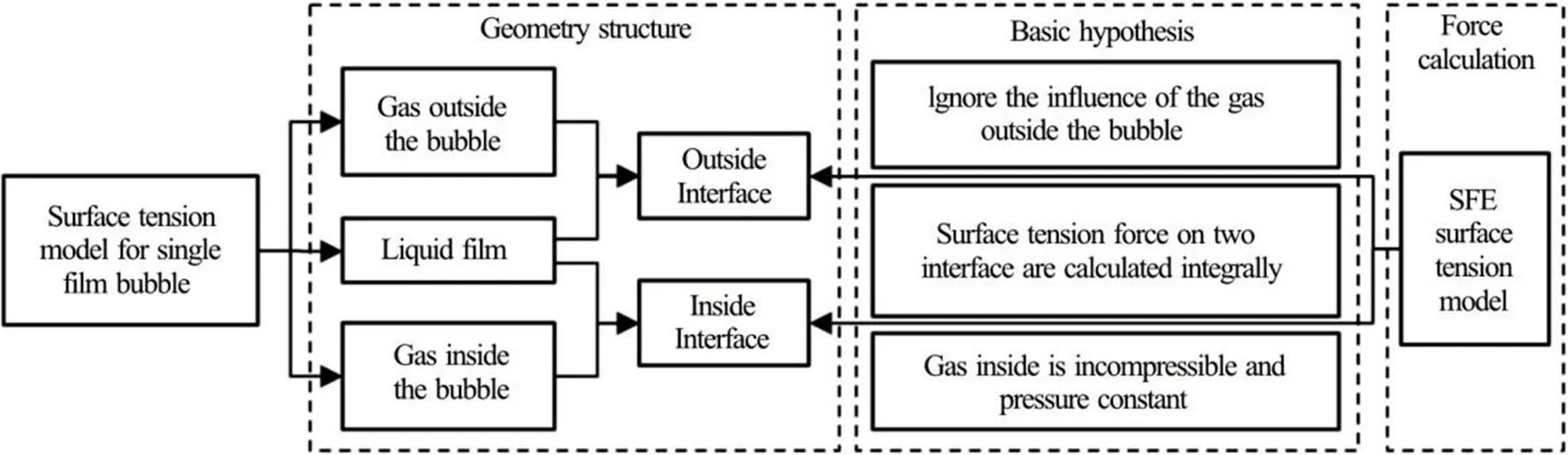
Fig. 2 Surface tension model for single film bubble
From Eq. (6), the surface tension calculation can be obtained as:

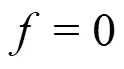
2.4 Improvement of SFE surface tension model
In this paper, in order to increase the accuracy of the SFE surface tension model to meet the high demand in a complex calculation, we improve the equation of the potential energy between particles from 1storder derivative to 2ndorder derivative. This modification would make the surface tension force more reasonable, and Eq. (7) is rewritten as:


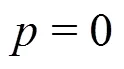
where


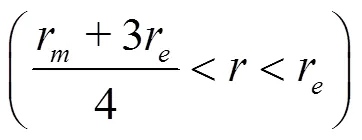
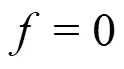
Fig. 3Comparison between the original and modified surface tension models


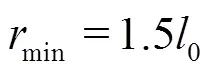

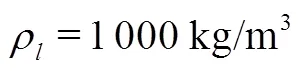
2.5 Oscillation of square single film bubble
The square single film bubble oscillation process is calculated with the modified SDST model as a classic validation case. The results are shown in Fig. 5. The single film is composed of three layers of particles including the outside layer, the inside layer and the inter layer between them. The gas outside the bubble is ignored, and the gas inside the bubble is incompressible and uniform which is not shown in these figures.
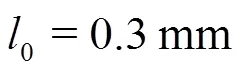

The pressure on the bubble film and the gas inside is shown in Fig. 6. It is shown that the pressure on the outside liquid film (the line with down triangles) is zero due to its opening in the atmosphere. On the inside layer of the liquid film (the line with up triangles) acts the same pressure as that of the gas inside (the line with squares) because they are open to each other. And the pressure is about 13 Pa, slightly higher than the pressure of the atmosphere outside.
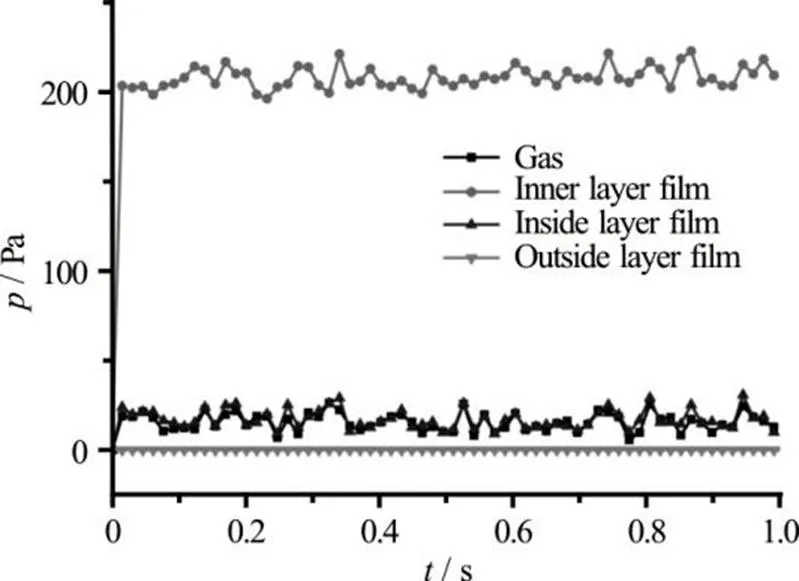
Fig. 6Pressure on the film and that of the gas inside the bubble
The pressure on the inter layer of the liquid film is higher than those on the other parts, because the composite force of the local surface tension forces points to the inner layer, which means that the inner layer liquid is squeezed by the two layers of the interfaces films.

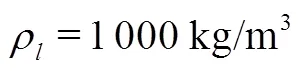
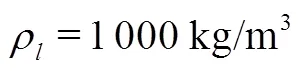
3. Numerical simulation and discussions
3.1 Coalescence of single film bubbles
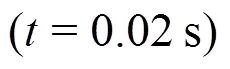
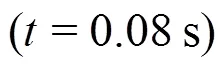
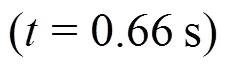
3.2 Connection of single film bubbles
The connection process of two single film bub- blesofdifferentsizesiscalculatedandtheresultsare shown in Fig. 8. In this simulation, the viscosity coefficient is set a larger value and the surface tension coefficient is set a smaller value than those in the last numerical cases shown in Fig. 7. The adjustment of these two parameters is in order to keep the connected film stable.
As shown in Fig. 8, the length of the connected film between the two bubbles grows with time, and reaches its largest value, when the connecting bubble system reaches its stable state.
The two connected bubbles are all in the scallop shape, and the connecting film is not straight because the pressures of the inside gas for two bubbles are different. Obviously, the gas inside the small bubble has a larger pressure and the connected film is curved and projects to the side of the large bubble.
It is notable that two single film bubbles con- nected with each other do not assume a new single round shape as the droplet, but in a parallel connection style that the whole outline of the assembly is decided by the local distribution of the surface tension force. The surface area of the connected bubbles can be estimated to be the smallest according to the inter- action between the gas pressure and the surface tension force.
3.3 Plateau structure in foam systems
When the connection process happens between three or more single film bubbles, a basic foam system is established, and the case of three bubbles of the same size is shown in Fig. 9. Three single film bubbles are located in three vertexes of an equilateral triangle, and a slightly adjustment is made to let two of them be connected first before the third one.

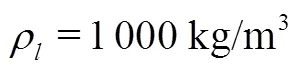
Fig. 10Pattern of three connected single film bubbles

The juncture area of the three bubbles is in a liquid trident shape, in other words, the liquid fully fills the gaps between the bubbles, and these liquid bridges or the tunnels are called in plateau structures, and they are the most common structures in a foam system.
The calculation results of the tri-bubble connec- tion and the plateau structure are compared qualitati- vely with the experimental results in Fig. 10. The angle between the branches of the plateau structure of the calculation agrees well with that of experiment.
However, the sides, the corners and their transi- tions between the plateau structure branches in the experiment are apparently clearer than those of the numerical results. That is because when the bubbles are connected to each other, the surface area is decrea- sed significantly, and also owing to the sharing of the film boundaries the liquid becomes more than needed. Therefore, a liquor drainage process would happen in the reality, however, this is not considered in the simulations of this study. In the authors’ opinion, the liquor drainage process is one of the important factors which would influence the detailed shape of the foam system.
4. Conclusions
Within the framework of the meshless moving particle semi-implicit method, a single-film double- gas-liquid-interface surface tension model (SDST) is proposed for simulating a single film bubble, which is the basic unit of the foam system. In view of the fact that the special structure of a single thin film wraps an amount of gas inside, the assumptions as the gas outside is ignored, the gas inside is incompressible, as well as even some physical characteristics are pro- posed. The surface tension force on the two sides of the film is calculated integrally using an improved surface free energy surface tension model, which is more accurate and stable.
Typical behaviors as the coalescence and the connection, and the feature structure as the plateau structure of the single film bubbles are simulated and reproduced, as well as the unsteady process under the surface tension, and the characteristics and the defor- mation details of a single film bubble. The numerical results of basic interactions between two or three bubbles provide some fundamental insight for related studies, and the SDST model prompts an efficient method to study the performance of the complex foam system.
[1] Chan D. Y. C., Klaseber E., Manica R. Film drainage and coalescence between deformable drops and bubbles [J]., 2011, 7(6): 2235-2264,.
[2] Yang L. T., Lv J. Q., Sun Y. H. et al. Theoretical analysis of leakage during the bubble size [J]., 2010, 39 (3): 78-79 (in Chinese).
[3] Zhang J. S., LV Q., Sun C. D. et al. High speed photo- graphy to motion of bubbles in water [J]., 2000, 29(10): 952-955(in Chinese).
[4] Gu H. Y., Guo L.J., Zhang X. M. et al. Single bubbles in gas-liquid two-phase flow in a horizontal tube shape characteristics [J]., 2006, 27(3): 433-436(in Chinese).
[5] Lu H., Shen Z., Ding J. et al. Numerical simulation of bubble and particles motions in a bubbling fluidized bed using direct simulation Monte-Carlo method [J]., 2006, 169(3): 159-171.
[6] Olmos E., Gentric C., Vial C. et al. Numerical simulation of multiphase flow in bubble column reactors Influence of bubble coalescence and break-up [J]., 2001, 56(21-22): 6359-6365.
[7] Liu H., Xie M. Z., Li K. et al. Liquid metal bath numerical simulation of bubble-liquid two-phase turbulent flow into metal melt [J]., 2007, 24(5): 669-673(in Chinese).
[8] Sungkorn R., Derksen J. J., Khinast J. G. Modeling of turbulent gas-liquid bubbly flows using stochastic Lagrangian model and lattice-Boltzmann scheme [J]., 2011, 66(12): 2745-2757.
[9] Chen L., Garimella S. V., Reizes J. A. et al. The develop- ment of a bubble rising in a viscous liquid [J]., 1999, 387: 61-96.
[10] Zhang S. J., Wu C. J. Numerical simulation of the inter- action between two three dimensional deformable bubbles [J].2008, 23(6): 681-686(in Chinese).
[11] Sussman M., Almgren A., Bell J. et al. An adaptive level set approach for incompressible two-phase flows [J].1997, 148(1): 81-124.
[12] Amaya-Bower L., Lee T. Single bubble rising dynamics for moderate Reynolds number using lattice Boltzmann method [J]., 2010, 39(7): 1191-1207.
[13] Yu Z., Yang H., Fan L. S. Numerical simulation of bubble interactions using an adaptive lattice Boltzmann method [J]., 2011, 66(14): 3441-3451.
[14] Koshizuka S. Oka Y. Moving-particle semi-implicit me- thod for fragmentation of incompressible fluid [J]., 1996, 123(3): 421-434.
[15] Sun Z. G., Xi G., Xiang L. F. Simulation on rising bubble in water with meshfree method [J]., 2007, 28(5): 771-774.
[16]Sun Z. G., Xi G., Chen X. A numerical study of stir mixing of liquids with particle method [J]., 2009, 64(2): 341-350.
[17] Sun Z., Xi G., Chen X. Mechanism study of deformation and mass transfer for binary droplet collisions with particle method [J]., 2009, 21(3): 032106.
[18]Chen X., Xi G., Sun Z.Improving stability of MPS method by a computational scheme based on conceptual particles [J]., 2014, 278(7): 254-271.
[19] Chen X., Sun Z. G., XI G. Improvement of the surface free energy model and numerical study on the infiltration of droplets [J]., 2012, 46(7): 115-121(in Chinese).
[20] Zhang S., Morita K., Fukuda K. et al. A new algorithm for surface tension model in moving particle methods [J]., 2010, 55(3): 225-240.
[21] Kondo M., Koshizuka S., Suzuki K. et al. Surface tension model using inter-particle force in particle method [C]., San Diego, California, USA, 2007.
(October 31, 2017, Accepted November 3, 2017)
©China Ship Scientific Research Center 2018
* Project supported by the National Natural Science Foundation of China (Grant No. 51576154).
Zhong-guo Sun (1981-), Male, Ph. D.,
E-mail: sun.zg@xjtu.edu.cn
Guang Xi,
E-mail:xiguang@xjtu.edu.cn
猜你喜欢
杂志排行
水动力学研究与进展 B辑的其它文章
- Spectral/hp elementmethods:Recent developments,applications, and perspectives *
- Influence of upstream disturbance on the draft-tube flow of Francis turbine under part-load conditions *
- Numerical study of the wave-induced slamming force on the elastic plate based on MPS-FEM coupled method *
- Gas-liquid flow splitting in T-junction with inclined lateral arm *
- 3-D Lagrangian-based investigations of the time-dependent cloud cavitating flows around a Clark-Y hydrofoil with special emphasis on shedding process analysis *
- The experimental study of hydrodynamic characteristics of the overland flow on a slope with three-dimensional Geomat *
