概率论教学中培养数学思维的探讨
2018-04-12李立明孙旭阳
李立明 魏 君 孙旭阳
(吉林大学数学学院公共数学教学与研究中心,吉林 长春 130012)
概率论是很多高等院校学生的一门重要的公共基础课,它是研究大量随机现象背后隐藏的统计规律性的一门学科,有别于其它研究确定性现象的学科。概率论的教学任务不仅是传授概率论的知识、思想和方法,更重要的是将概率论的思维方式渗透到教学过程中,启迪学生的智慧,挖掘学生的潜能,培养学生的数学思维能力以及创新能力。本文结合教学实际,对概率论教学中如何培养学生的数学思维进行了一些探讨。
一、引导学生将随机性思维和确定性思维有机结合
高中数学中对概率论就有了简单的介绍,但是只讲述如何求概率,并没有给出概率的严格的数学定义。而大学阶段的概率论的基础是微积分、线性代数,更加严谨抽象和晦涩难懂。从课程开始就引导学生用新的思维方式——随机性思维来思考、分析和解决问题非常重要。
传统的确定性思维认为所有的问题的答案都是独一无二的,完全确定的,然而现实世界中的很多问题都没有程式化的确定答案,像“明天是否下雨”“股票是否上涨”等,根本原因在于生活中随机现象的广泛存在。因为随机现象是大量微小的随机因素共同作用的结果,所以对于随机现象,谁都不可能完全准确无误的预测,就连确定性的数学模型也是忽略掉诸多次要因素才得以产生。
例如抛一枚硬币,可能出现正面,也可能出现反面,正反面的出现是随机的,谁也不能百分百地预测。但是如果将一枚硬币重复地抛很多次,却可以预言大约50%次数出现正面或反面。也就是说,虽然随机现象具有偶然性,但是大量随机现象却蕴含着必然性。概率论最重要的极限定理之一“大数定律”的核心思想就是:大量随机现象的平均结果具有稳定性。概率论就是要教学生用随机的眼光,透过表像的偶然,寻求内部的必然。
大千世界,随机因素无处不在起作用。概率论与实际生活息息相关,在各行各业、各个领域中应用也十分广泛。在概率论的教学中,如果教师能在确定性思维基础上,引导学生用随机性思维来思考、分析和解决问题,并能学以致用,解决生活中的概率问题,不仅会提高学生的思维品质,还能培养创新能力。
二、引导学生将辩证思维和概率论思维有机结合
概率论中包含着大量的辩证法思想,比如偶然中蕴含必然,量变积累产生质变、无限与有限的转换,等等。教师如果在教学中能合理渗透辩证法思想,引导学生将辩证思维和概率论思维有机结合,可以更好地帮助学生理解教学内容,将概率论深刻的思想内涵,内化为自身的数学素质,提高智力品质,完善思维结构。
1、量变到质变的辩证思维
在概率论中,我们把概率很小(接近于0)的事件称为小概率事件。小概率事件在一次试验或少量的几次试验中,虽然有可能出现,但是出现的可能性很小,可称为“几乎不可能”事件。但是在大量重复独立试验中,小概率事件的概率会变得接近于1,成为大概率事件。因为大概率事件出现的可能性很大,可称为“几乎必然”事件。
例如:假设白菜种子中混有0.4%的油菜种子,从一大口袋这样的种子中任取100粒或1500粒,计算取出的种子中有油菜种子的概率。
解:以Ai表示所取出的第i粒种子为油菜种子(i=1,2,…,n),由题意可以认为各个事件Ai(i=1,2,…,n)相互独立,因此取出的n粒种子中有油菜种子的概率为
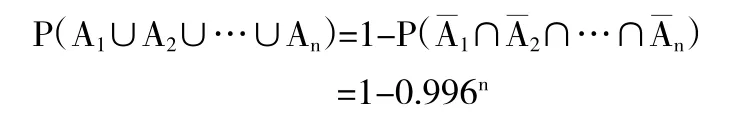
取出的100粒种子中有油菜种子的概率为
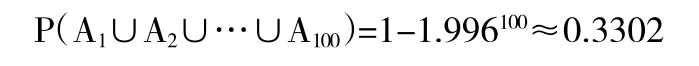
取出的1500粒种子中有油菜种子的概率为
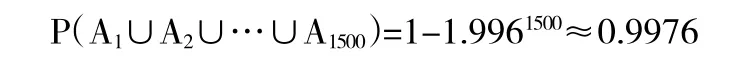
从小概率0.004到大概率0.9976的转变,或者说从“几乎不可能”事件到“几乎必然”事件的转变,不是一蹴而就的,是伴随着试验次数的不断增加而逐渐产生的。试验次数越多,小概率事件出现的可能性越大。随着试验次数的不断增加,小概率事件的概率经过“量”的不断积累,最终突破了一定的“度”,产生了“质”的飞跃,变成大概率事件。
2、有限与无限的辩证思维
以几何概型为例,它也称无限等可能概型,特征是样本空间的样本点无限多,连续地充满某个区间、平面区域或立体区域,且每个样本点的出现都是等可能的。几何概型中概率的计算,本来是对无限多的样本点的运算,但是可以通过改变计量方式,转化成对有限的区间的长度、有限的平面图形的面积或有限的空间立体的体积的运算。简单地说,在一定条件下,无限可以转化为有限。
例如:将长为m的线段任意折成三段,求所得三段能构成三角形的概率。
解:设所折三段长分别为x、y及m-x-y,应满足
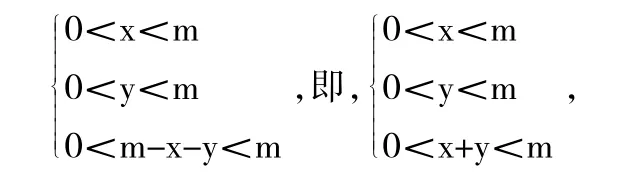
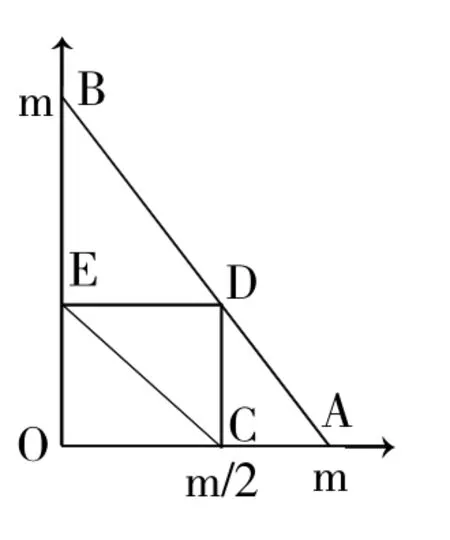
样本空间的样本点(x,y)构成△OAB。
所折三段能构成三角形,应满足
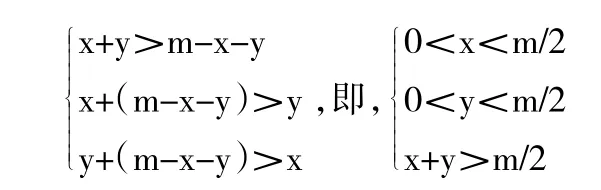
此事件的样本点(x,y)构成区域△CDE。从而所求概率为
反过来,有限也可以转化为无限。以概率的定义为例,概率是度量事件发生可能性大小的数,这个数是事件本身所固有的,它是一个位于0和1之间的有限的数。由概率的统计定义和伯努利大数定律可知,这个数可以用无限增大试验次数的方法,利用频率的稳定值获得。
三、引导学生将聚合性思维和发散性思维有机结合
聚合性思维也可以叫收敛性思维,是在一定范围之内有固定规则和确定方向的思维模式,强调的是对已有信息的理解和综合使用。反之,发散性思维是没有范围、规则和方向的思维模式,海阔天空任凭想象,强调的是对新信息的联想和综合运用。
在概率论的教学过程中,如果一味地强调聚合性思维,缺少对发散性思维的鼓励,会僵化学生的思想,束缚学生的想象力,使学习过程变得教条和枯燥,易使学生失去学习概率的兴趣和动力。相反,教师如果能在聚合思维基础上,恰当地引导学生运用发散性思维,鼓励学生展开想象的翅膀,鼓励学生从多角度、多方面思考问题,就会极大地调动学生的热情,积极主动参与到学习中。
聚合性思维和发散性思维的有机结合,使学生在学到数学知识的同时,思维能力也得到了拓展,数学素质有了进一步提高。
解题教学是概率论教学中比较重要的一个环节,概率论中的新的概念、方法等都需要通过解题训练得以巩固。在概率的解题过程中,一题多解就是发散性思维的一个体现。
例如:有10个人随机地绕着一个圆桌而坐,求张三、李四两个人座位相邻的概率。
解法1:按照圆周排列的方法求解。10个人中的第一个人有10个座位可以选择,第二个人有9个,第三个人有8个,照此类推共有10!种坐法。可以注意到:每一种坐法经过旋转都可以产生10种坐法。因为圆桌排列不用考虑排头,所以这10种坐法是重复的。去掉重复的坐法,10个人绕圆桌而坐共有9!种坐法。李四和张三座位相邻看作占一个座位,两人座位可以交换,故有2×8!种坐法。故所求概率为
解法1是常规解法,属于聚合性思维。这种解法的训练,可以巩固学生对所学知识的理解和熟练运用。
解法2:不妨假设张三先坐下,那么张三有10种坐法,相应于张三的每一种坐法,李四在剩下的9个座位中选择一个,即李四有9种坐法,即基本事件总数为9,而李四和张三座位相邻有2种坐法,故所求概率为
解法2去繁求简,假设一个人先坐下,着重关注另一个人的坐法,在缩小了的样本空间中求解。这种解法简单独特,标新立异,从不同的角度思考问题,拓宽了学生的思路,锻炼了发散性思维。
四、引导学生将批判性思维和概率论思维有机结合
批判性思维,是指用质疑、批判、否定的态度,大胆破除思维惯性的束缚,在思维的过程中不断地作出评判。批判性思维表现为能独立思考,不盲从,有个人独到的见解和判断。
批判性思维既是求异思维,也是创造性思维。
在概率论的教学中,引导学生将批判性思维和概率论思维有机结合,鼓励学生对所研究对象的真实性、价值做出评判,这种评判当然不是对已有知识的完全否定,而是对已有知识的扬弃、发展和创新。
例如:某地罹患癌症的人占0.005,罹患癌症的人对一种医学检验反应是阳性的概率为0.95,健康人对这种检验反应是阳性的概率为0.04,在该地随机抽查了一个人,检验结果是阳性,问此人罹患癌症的概率有多大?
解:设C={抽查的人患有癌症},A={试验结果是阳性},所求概率为 P(C|A)。根据贝叶斯公式由题意,P(C)=0.005,P(C)=0.995,P(A|C)=0.95,P(A|C)=0.04,带入数据进行计算得P(C|A)=0.1066,即检验结果为阳性的人罹患癌症的概率为0.1066。
在讲解这个概率问题时,教师对运算结果不要一带而过,应引导学生大胆质疑,对所研究结果的真实性、价值做出评判。比如检出阳性的人是否一定患有癌症?这种试验对于诊断一个人是否患有癌症到底有无意义?如何进一步提高试验的价值?等等。批判性思维不仅可以调动学生的热情,提高学生主动参与的意识,还能提高学生的识别、反驳和重建的能力,提高学生思考问题的严谨性、深刻性。
总之,在概率论的教学中加强数学思维的培养,可以使学生更深刻地理解概率论的知识、思想和方法,还可以引导学生用数学思维去分析、解决实际生活中的问题,增强应用数学的意识和创新能力。数学教师应当明确大学生素质教育的目标,根据概率论的学科特点,积极研究并实施数学思维教育,促进大学生综合素质的全面发展。
参考文献:
[1]张德然.概率论思维论[M].北京:中国科学技术大学出版社,2005.
[2]徐静.概率论教学中思维品质的培养[J].大学数学,2011,(5).
[3]徐香勤,刘花丽.论概率论教学中的思维方式的培养[J].和田师范专科学校学报,2010,(3).
