生命探测信号在强震作用下的波动特性分离*

吴义满

(江苏医药职业学院，江苏 盐城 224000)

事实证明，抢救被困人员的黄金时期在于震后72 h以内，对震后压埋人员的救援愈准确及时，受灾人员存活的几率愈大[1]。回顾汶川大地震，在当时的复杂情况下进行实时有效的救援成了一大难题。为更好的保障国民生命财产安全，对生命信号的准确搜索和判断提出了更高的要求。为了达到在最短时间内找到被困人员的救援目的，保障强震后能够快速有效的进行救援行动，需要深入探索和研究更先进的救助设备和生命探测定位技术，这对于保障人民生命财产安全方面具有十分重要的意义。现阶段的生命探测技术包含对人体的声音、移动、心跳、热能以及静电场等特征的探索，是在特殊环境下对生命特征搜索和检测的重要方法[2]。生命探测是采用现代化技术和手段在特殊情况下对生命信号进行检测和分析的过程，通过电磁波的波动判定生命体是否存活。由于周围温湿度以及外界噪音等因素等对电磁波干扰相对较小，因此研发电磁波生命信号搜救技术在生命探索方面越来越受到人们的关注。基于以上原因对连续波的工作原理的研究以及对生命信号的提取和建模，提出微型声波生命探测方法并进行仿真实验，效果良好。

1　波动特性分离算法

电磁波生命信号搜救模型的建立基于微型声波生命探测技术以及波动性分离算法，为实现波动特性分离算法首先需要获得在生命探测器发射连续波情况下的信号频率A(t)，表示为：

(1)

式中：z为生命信号探测仪的发射波频率；t为振幅；λ为信号波动的初相位[3]。通过上述公式可推出，生命探测仪在探索过程中接收到目标的回波信号频率An(t)为：

An(t)=PA(tn-t)=Pλcos[2πz(tn-t)+λ]。

(2)

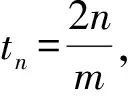
D=Y0-ztn。

(3)

式中:Y0为t=0时的距离， 通过公式(1)(2)(3)将回波信号与发射信号进行分离，其差值为:

δ=βcos(2πzt+λ)-Pλcos[2πz(tn-t)+λ]+2πftn

公共基础教学课程作为四年制高职学生的基础课程，是学生培养良好职业道德、练就较强专业知识技能、养成终身学习能力的核心课程，因此加强公共基础课教师队伍建设，提升公共基础课教师队伍素质是更好服务四年制高职公共基础教学的当务之急。师资队伍建设要敢于结合当前发展潮流，结合省情和学院情况，积极引进与四年制高职学生培养目标相适应的教师人才；要有计划地组织安排在职公共基础课教师参加有助于专业发展与拓宽视野的培训活动；进一步更新高职教育思想观念、加强自身修养、主动树立服务专业的意识，充分认识到公共基础课程对学生综合素质培养的作用，帮助学生做好职业生涯规划。

(4)

通过公式(4)算法可推出发射信号与接收信号分离波动频率为:

(5)

电磁波照射到人体目标时，生命体的振动限定于有限范围内，接收到的信号围绕着平均距离W上下波动[4-5]。电磁波与生命体信号的瞬时波动距离W(t)可以写成下面的形式:

W(t)=fmAn(t)+ΔW(t)。

(6)

式中:ΔW(t)表示生命体心跳和呼吸等特征信号引起的皮肤波动频率，可通过下述公式求得生命体特性波动频率为：

ΔW(t)=A(t)sin(2πfmtn+δ)-An(t)sin(2πfmtn+λ)。

(7)

通过对信号破洞频率和距离的推导得出特性波动分离信号F(t):

F(t)=A(t)W(t)-cos(2πΔW(t)-fmtnδ-zλ)。

(8)

根据以上公式对生命体目标频率和探测器的发射频率结果进行测量具体探测结果如图1所示。

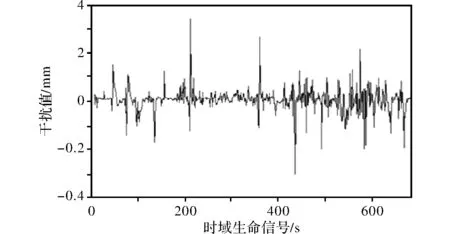
图1　生命信号时域方针测量结果

因此，我们只要测量目标的频率与径向速度，并根据上述公式进行计算就可获得目标的运动速度，从而对检测目标的特性进行判断[6]。用分离后的信号进行微型声波探测模拟技术来完成震后生命信号检测工作。

2　微型声波生命探测模型

通过上述计算可知，在高频区电磁波谱中探测的生命目标信号是由生命体局部位置散射所合成，局部目标散射中心是在高频频区散射的基本特征之一[7]。假设生命体位于障碍物后1～1.5 m处，在障碍物的另一端进行搜索和探测，效果如图2所示。

探测器发射的部分信号会在墙面折射部分信息，其余大部分穿墙辐射到人体部分。根据散射中心特性，在生命体的主要骨骼衔接处形成散射点[8]。探测原理如图3所示。相同x坐标，任意散射点在视轴上形成一个中心，在该散射中心范围内的各点时延由坐标位置决定[9]。

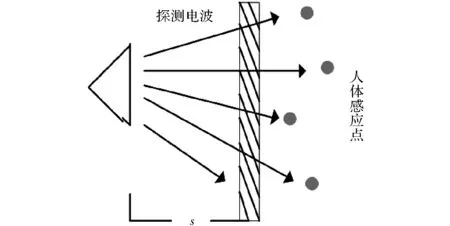
图2　人体探测仿真图

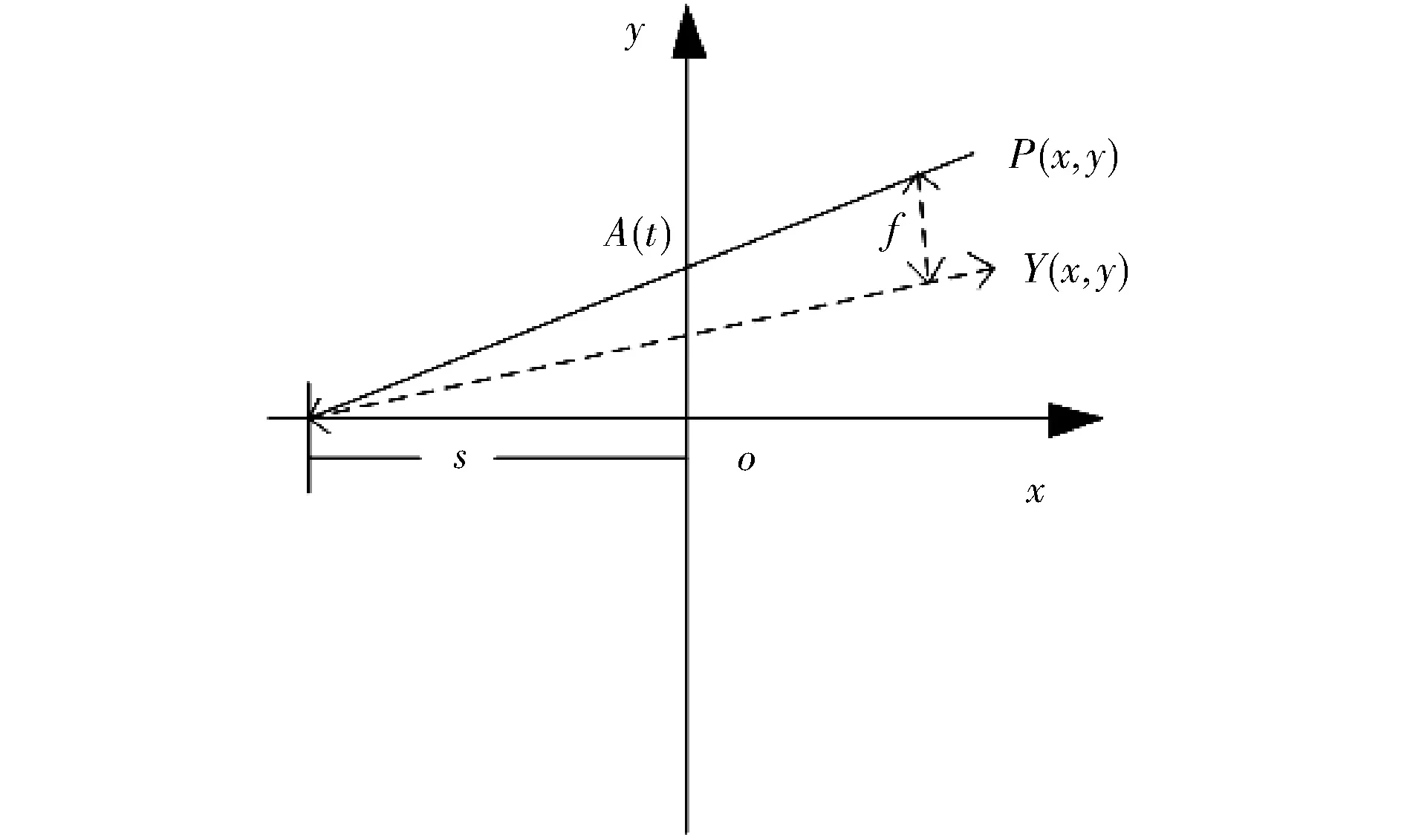
图3　微型声波二维坐标系模拟示意图

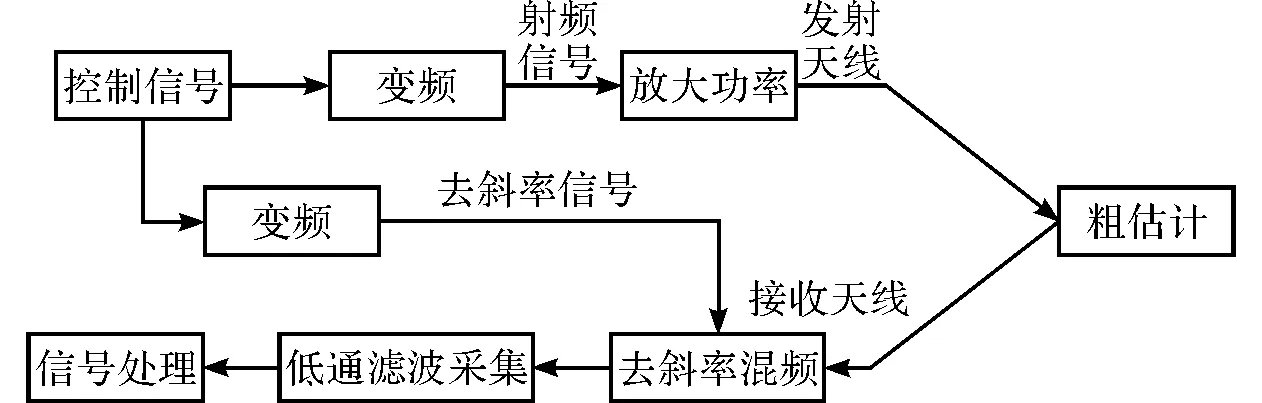
图4　微型连续波工作原理

微型连续波生命探测的基本工作原理如图4所示。图4给出了连续波的最简单形式。探测仪调频连续波形，通过天线发射在遇到生命体目标后返回。在接收端进行接收信号去斜率混频以得到探测目标特性判定生命体的有无[10]。连续波的频率变化会随时间呈线性变化。图5、图6、图7给出了线性调频波的时频曲线、时域波形和幅频特性。

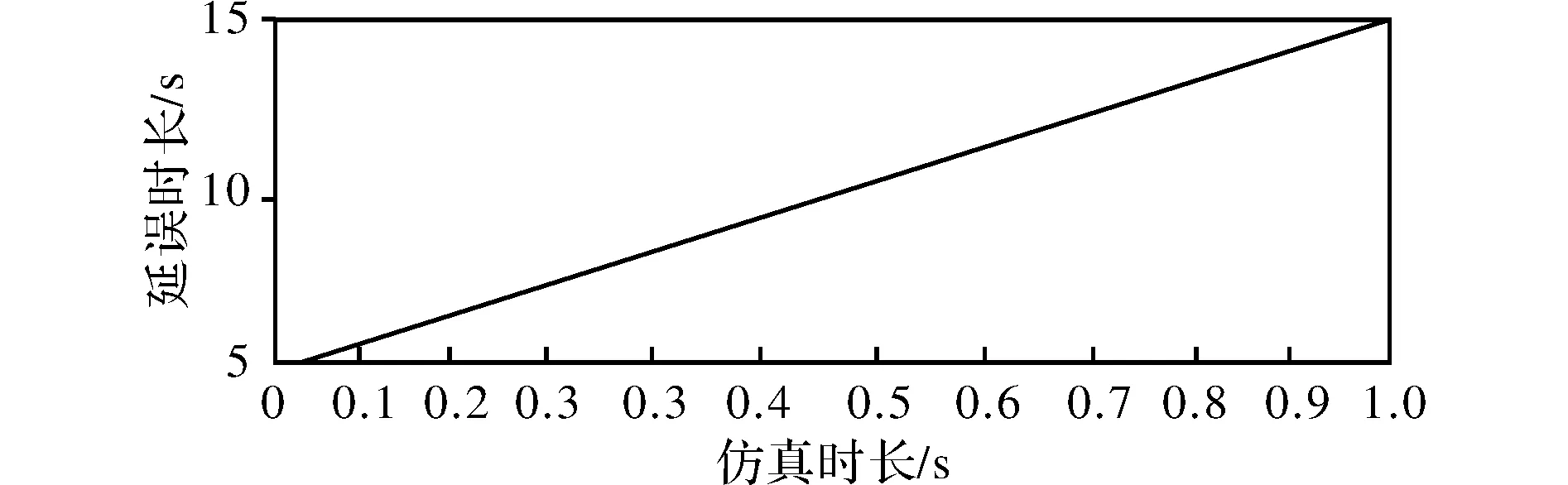
图5　线性调频波的时频曲线

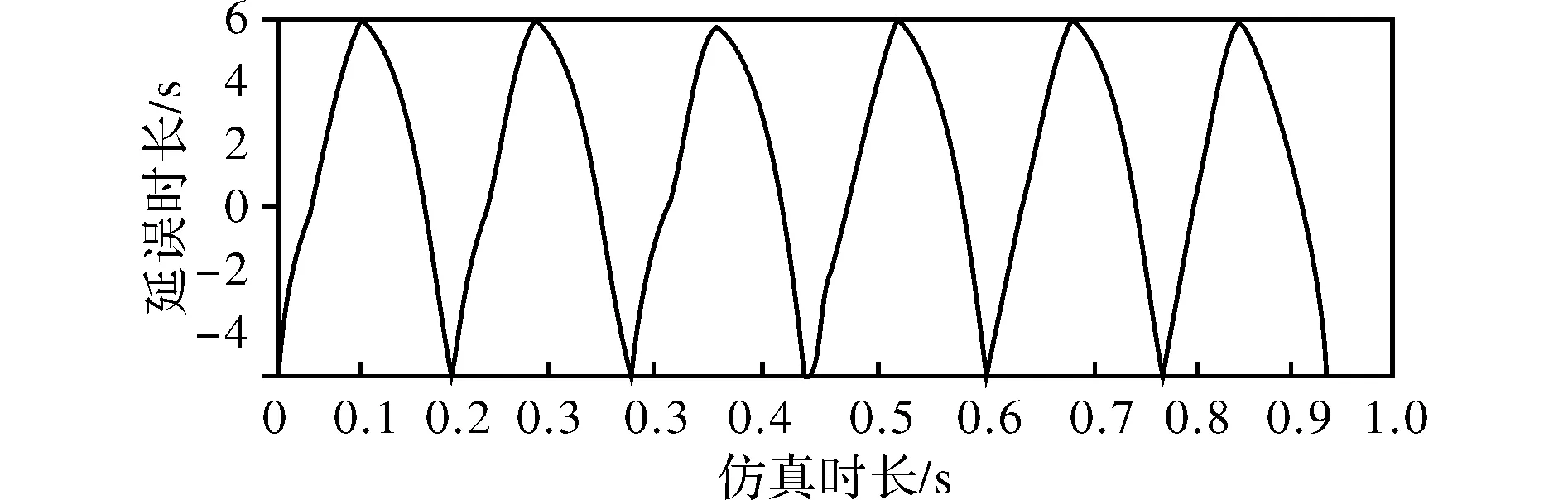
图6　线性调频波的时域波形

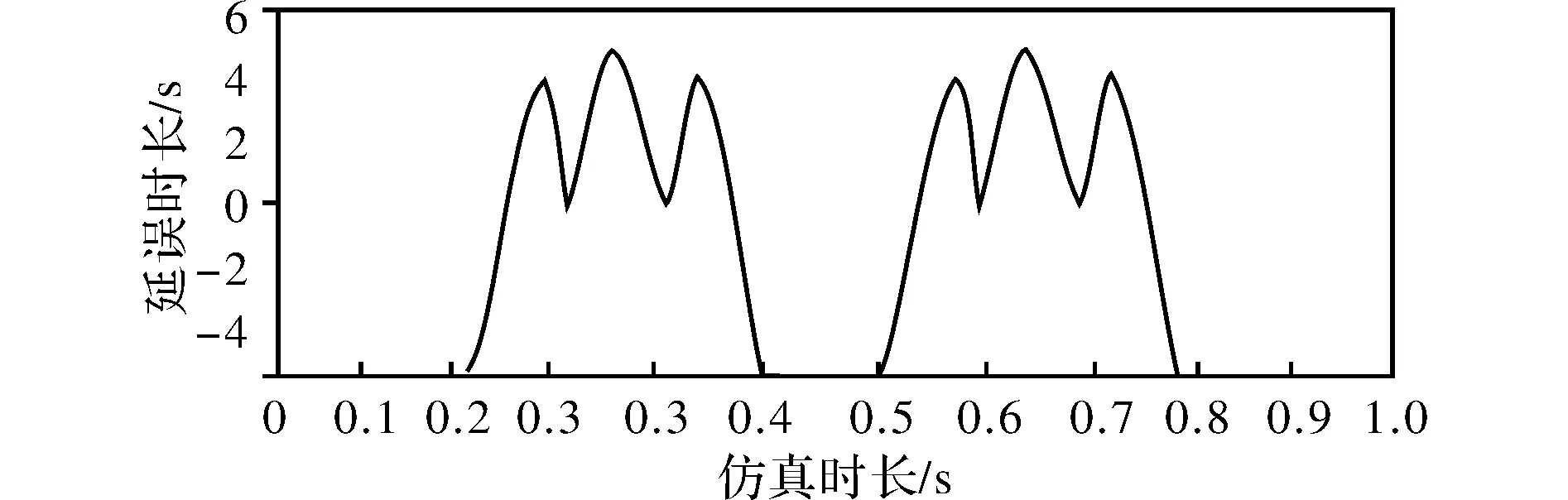
图7　线性调频波的幅频特性

连续波信号仿真如图7所示，在接收到的生命体回波信号中，接收与发射信号的瞬时频率差通常是一个常数，对接收信号与发射信号的频率差进行测量可得到目标距离[11-12]。再通过混频处理得到频率差，处理方法如图8所示。

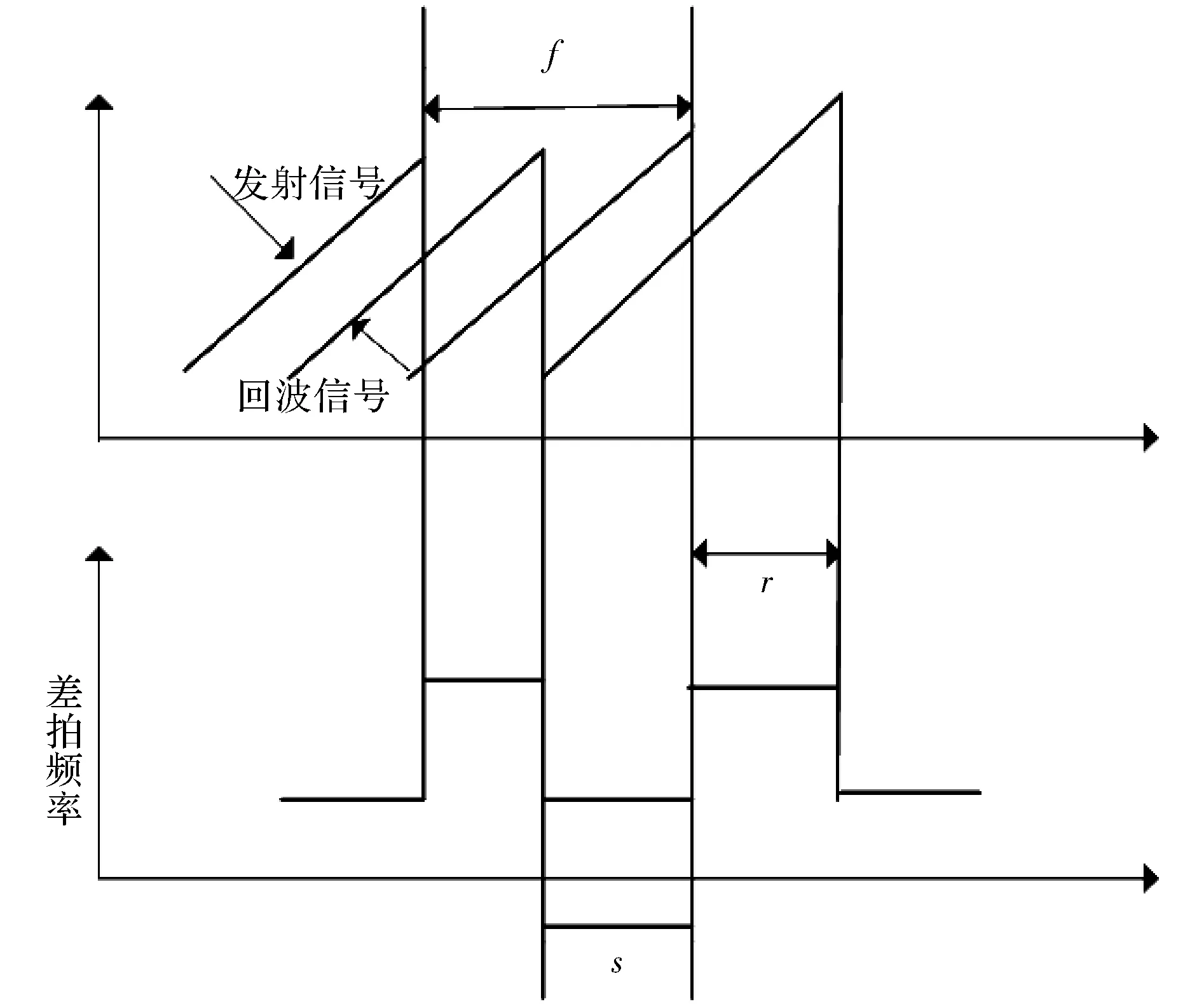
图8　微型声波生命频率信号差探测方法

由此可以看出人体生命信号探测可以根据回波信号测定生命体有无呼吸和心跳达到电生命信号检测的目的[13]。对上述方法进行仿真测量结果如图9所示。

图9结果可以看出在心跳和呼吸这种微动情况下利用微型声波生命频率信号差的方法探测生命信号效果性对比较明显。

图9　微型声波生命信号探测频率差仿真测量结果

3　实验结果分析

实验一:模拟震后环境在测量范围内完成4个目标的探侧，两个健康人体安静坐于30cm厚水泥墙后，顺序改变延迟时间，查看中频信号输出和最终目标信噪比。实验情况见表1。表1信息证实微型声波生命探测能够穿越较厚障碍物对生命体信号特征进行及时的检测和准确的分析。

表1　系统经输出目标信息

实验二:实验测得四个生命体呼吸信号的频谱如图10所示。从实验结果可以看出后者比前者信息更加丰富，这是由相邻操作者的影响引起的。由此可以看出生命信号可以采用型声波生命信号探测方法进行测量，根据回波信号判断生命体有无呼吸和心跳，从而做到快速精确检测生命信号的目的。

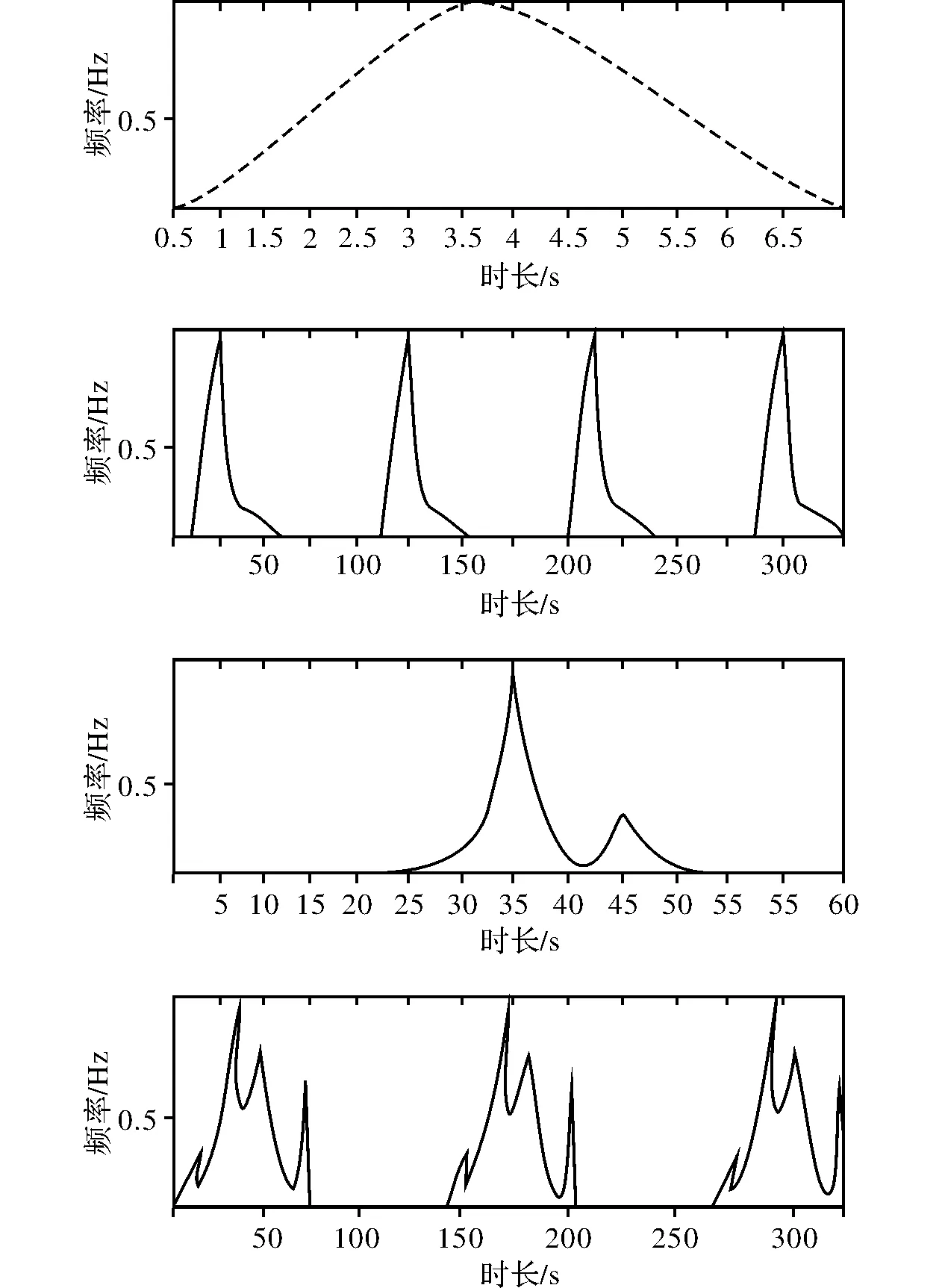
图10　生命目标特征探测结果对比图

4　结束语

为达到更精准快速的探索生命信号的目的提出利用微型声波进行生命探测的与方法，依托对微型声波生命探测机理的研究成果，进行软件数据的计算和仿真实验来验证方法的可行性，同时通过硬件设计，创新微型声波生命探测模型，以便修正和完善微型声波生命探测理论。

参考文献：

[1]张桂南, 刘志刚, 向川,等. 多频调制下电气化铁路电压波动特性分析及频率估计[J]. 电网技术, 2017, 41(1):251-257.

[2]肖丹, 吴婷茜. 网络波动攻击中的小扰动入侵源定位算法仿真[J]. 科技通报, 2015, 31(12):179-181.

[3]张亢, 石阳春, 唐明珠,等. 局部波动特征分解及其在滚动轴承故障诊断中的应用研究[J]. 振动与冲击, 2016, 35(1):89-95.

[4]管西竹, 陈宝书, 符力耘,等. 基于波动方程的上下缆地震数据鬼波压制方法研究[J]. 地球物理学报, 2015, 58(10):3746-3757.

[5]吴永恒, 肖涵. 基于自适应非趋势波动分析的齿轮振动信号特征提取[J]. 振动与冲击, 2015, 34(9):154-157.

[6]陈卫军, 睢丹. 基于扰动特征分解和前馈调制的网络波动跳变信号抑制算法[J]. 计算机科学, 2015, 42(7):165-169.

[7]刘文兴, 赵大卫, 苏光辉,等. 流量波动作用下临界热流密度特性理论模型开发与验证[J]. 核动力工程, 2016(5):125-129.

[8]刘强, 白鹏, 李锋. 不同雷诺数下翼型气动特性及层流分离现象演化[J]. 航空学报, 2017, 38(4):22-34.

[9]毛钰, 左曙光, 林福,等. 转矩波动下电动轮纵向阶次振动特性及理论分析[J]. 同济大学学报(自然科学版), 2016, 44(11):1735-1742.

[10] 王伟华, 张子娇, 周海波,等. 一种同步直线电机推力波动特性的检测方法[J]. 中国电机工程学报, 2016, 36(2):540-546.

[11] 韩志强, 任川江, 曾东建,等. 高压共轨柴油机怠速循环波动特性[J]. 长安大学学报(自然科学版), 2016, 36(5):95-102.

[12] 吴振信, 万埠磊, 王书平,等. 欧盟碳价波动的结构突变特性检验[J]. 数理统计与管理, 2015, 34(6):969-977.

[13] 周鑫, 黄创霞, 谭艳祥. 风电功率波动特性研究[J]. 湖南文理学院学报(自科版), 2015，54(2):39-42.