APOSOS项目15 cm光电望远镜故障监测方法研究*

蔡炀烁，高鹏骐，沈　鸣，于欢欢，郭效忠，杨大陶，赵　有

(1. 中国科学院国家天文台，北京　100101；2. 中国科学院大学，北京　100049)

1　背　景

自1957年前苏联发射第1颗人造卫星以来，空间碎片的数量与日俱增。愈来愈多的飞行器被发射到太空，围绕地球运行的火箭体、失效卫星、飞行器及产生的碎片也随之越来越多，进而对航天器的安全形成巨大的威胁。因此对空间碎片进行监测，是更多国家关注的问题[1-3]。

亚太地基光学空间物体观测系统(Asia-Pacific Ground-based Optical Space Object Observation System, APOSOS，以下皆简称为APOSOS)是亚太空间合作组织(Asia-Pacific Space Cooperation Organization, APSCO)设立和支持运行的项目，意在联合其成员国，发挥各国的经济、技术及地域优势，建立一个区域性乃至全球性的光学观测网络，实现空间目标的捕获、跟踪与测量，为在轨航天器的管理、使用与安全运行提供保障，为未来航天器的发射提供服务[4]。

APOSOS项目15 cm望远镜系统主要由跟踪架、光学系统、成像探测器、时间系统、主控计算机、配电等组成，望远镜主要参数见表1。

目前首批15 cm地平式光电望远镜已经研制完成，并部署到位于亚太空间合作组织所属成员国的节点，由当地的科技人员根据观测计划对感兴趣的卫星与碎片进行跟踪观测，观测完毕后将数据传送到位于中国科学院国家天文台的数据与运行管理中心。由于数据与运行管理中心在各成员国节点并无驻守人员，为掌控各望远镜的状态，便于指导当地科技人员对设备进行维护，非常有必要研究一种通过观测数据对望远镜状态进行监测和故障诊断的方法。

本文提出了一种联合使用天文定位与轴系定位数据对望远镜状态进行动态监测的方法。通过综合分析天文定位与轴系定位误差，由轴系定位的观测误差及稳定性判断望远镜跟踪硬件的工作状态是否正常，进而提出诊断方向与维护意见。该方法不仅解决了15 cm望远镜的动态监测问题，对于其它无法现场检测的远程控制站点和无人值守望远镜的监控也有重要的参考价值。

2　数据来源与计算方法

2.1　数据来源

APOSOS项目15 cm望远镜输出的观测数据分为方位-高度和赤经-赤纬两类，分别来源于轴系定位与天文定位。轴系定位是以安装在望远镜轴上的码盘读数为基础进行定位，而天文定位是以视场中多颗恒星的位置为基准进行定位。轴系定位得到的方位角与高度角，与观测者位置相关，不同台站、不同时间观测的数据不在同一坐标系下。而天文定位得到的位置信息是赤经和赤纬，经简单换算，任何测站、任何观测时间的观测数据均可视为处于同一个稳定的坐标系中。轴系定位的测量误差取决于望远镜轴系读数的精度、目标在CCD上读数的精度、望远镜轴系的稳定性、大气折射改正的精度。天文定位的测量误差不受望远镜轴系误差和大气折射改正误差的影响，主要取决于定标星个数、卫星或空间碎片的运动速度、恒星和卫星星像的测量精度。天文定位是目前光电望远镜观测跟踪空间目标的主要方法[5-9]。

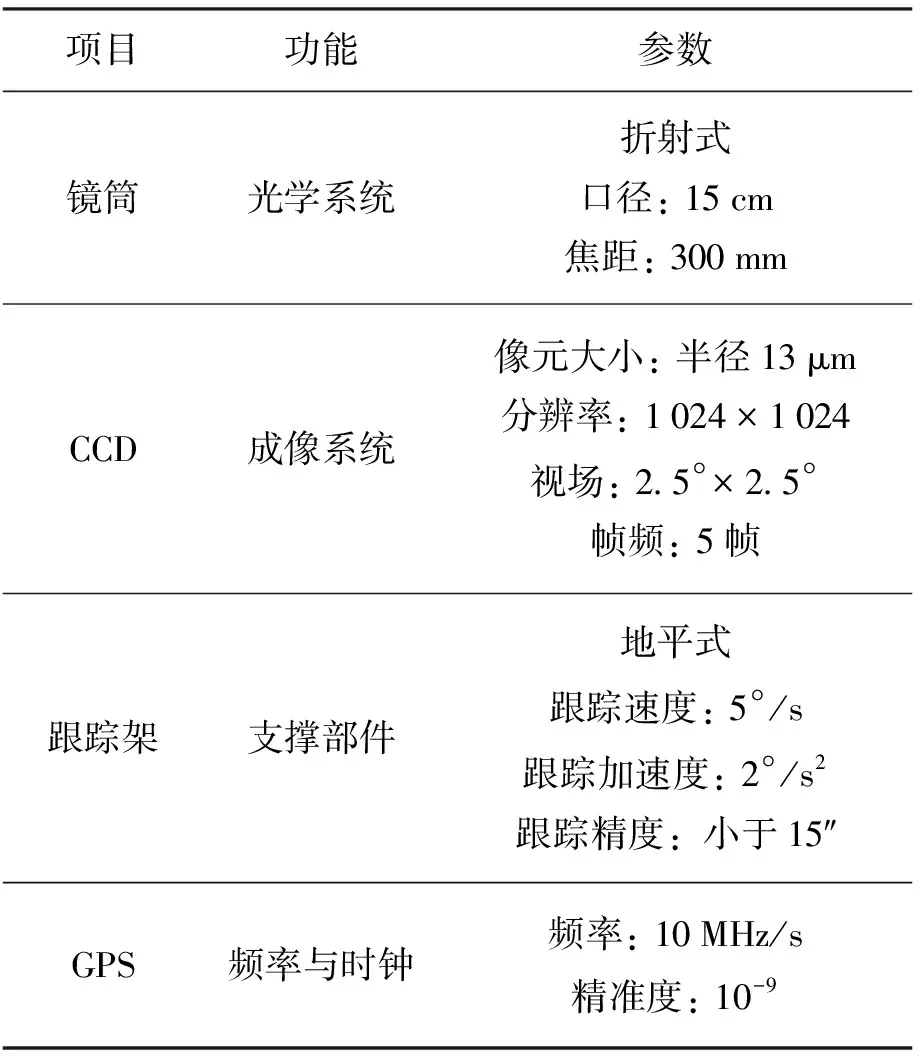
表1　15cm望远镜主要参数Table1　Parametersofthe15cmtelescope

本文所用的原始数据来自于安置在伊朗和巴基斯坦观测站的15 cm折射式地基空间碎片光电望远镜(下称1号设备与2号设备)，以及1号设备在中国长春的测试观测数据。要分析设备的测量误差，需对两台设备的天文定位、轴系定位分别进行外符精度判定。观测数据包括观测卫星的轴系定位

数据和天文定位数据。两台设备观测的卫星信息见表2。

2.2　计算方法

对望远镜状态的动态监测采用天文定位与轴系定位误差对比的方式，由轴系定位的观测误差及稳定性判断望远镜跟踪硬件的工作状态是否正常。

对望远镜观测数据的误差一般采用外符精度的评估方式。外符精度评估是指利用与待评估设备相互独立的、得到广泛认可的观测手段，得到的高精度精密星历，与待估设备实测的观测数据做比较，以确定待估设备的测量误差[10]。激光测距是目前空间目标观测手段中精度最高的一种，对合作目标的测距精度可优于1 cm，预报一天的轨道误差在几十米量级，利用激光测距资料通过精密定轨软件计算得到的精密轨道可近似认为是真实轨道、理论真值。以此作为外符精度评定依据，得到的评定结果具有合理性以及可靠性。目前，国际激光测距网(International Laser Ranging Service, ILRS)可观测的卫星高度从几百千米到几万千米，可以根据光电望远镜的探测距离灵活选择适当的卫星。因此，选取利用卫星激光测距技术获取的高精度星历作为观测数据外符精度判定的标准。整个过程简述如下：

表21号、2号设备观测的卫星编号及观测时间

Table2NumberandobservationtimeofsatellitesobservedbyequipmentNo.1andNo.2

设备卫星编号卫星名称观测时间1号设备41240JASON32017/02/0615h12min33105JASON22017/02/0616h8min39086SARAL2017/02/0616h13min2017/02/1916h9min2017/02/2516h22min40890GALILEO10(206)2017/02/0617h7min41241IRNSS⁃1E2017/02/1915h54min2号设备39086SARAL2017/01/0514h34min2017/02/0914h43min2017/02/171h32min41240JASON32017/02/100h24min1号设备27386ENVISAT2016/09/1911h51min在国内2016/09/2012h54min观测39086SARAL2016/09/2011h14min36508CRYOSAT22016/09/2013h7min

(1)使用15 cm望远镜观测一颗由国际激光测距网支持的卫星，获得记录有卫星观测时刻和空间位置的光学观测数据。

(2)从国际激光测距网下载高精度星历。

(3)对高精度星历进行内插，计算到与实际观测时刻一一对应，以生成卫星的理论位置(“真实值”)。

(4)使理论位置与观测位置处在同一参考系中。

(5)计算残差。

利用卫星激光测距数据得到的观测时刻理论的赤经赤纬值是J2000.0惯性坐标系中的。在i时刻，J2000.0惯性坐标系中空间目标的位置矢量为Ri(xi,yi,zi)，测站的位置矢量为Rsi(xsi,ysi,zsi)，则空间目标在站心历元平赤道坐标系的位置矢量RJ2K(xJ2K,yJ2K,zJ2K)为

RJ2K(xJ2K,yJ2K,zJ2K)=Ri(xi,yi,zi)-Rsi(xsi,ysi,zsi)，

(1)

此时，空间目标的赤经赤纬理论值αc和δc为

(2)

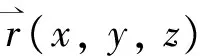
(3)

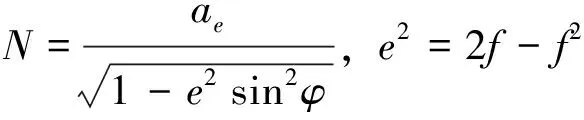
(4)

其中，λ，φ，h分别为测站的经度、纬度和海拔高度；ae为地球赤道半径；f为地球扁率。因此测站的地心地固坐标为

(5)

对卫星的精密轨道星历做ti时刻的插值计算， 利用插值后的卫星精密轨道由(3)式计算得到理论的赤经赤纬值αc和δc。由中误差公式：

(6)

分别求出赤经α和赤纬δ的中误差σα和σδ，其中，yi为观测值与理论值之间的残差，αi的残差用[αi-(αc)i]cosδi表示。

为得到轴系定位的测量误差，需要先得到被观测卫星的地平坐标系理论坐标。有两种途径。第1种是将国际激光测距网支持的激光卫星观测时刻的站心地固参考系坐标，转化到地平坐标系的方位角高度角坐标。而对于非激光卫星，则需要第2种途径，首先将地心天球坐标系的天文定位视为可靠的理论位置，再把观测时刻理论的赤经赤纬值，转化成对应时刻同一测站的方位角和高度角的理论值。流程见图1，GCRS为地心天球坐标系，MOD为瞬时平赤道平春分点坐标系，TOD为瞬时真赤道真春分点坐标系，PEF为伪地固参考系，ITRS为地固参考系。要将地心天球坐标系的坐标转换到地固参考系坐标，再将地固参考系坐标转换到地平坐标系的方位高度坐标[5]。需要注意的是，地心天球坐标系与J2000坐标系有细微的差异，由于其他的误差来源远远大于这两个坐标的差异，因而在人卫工作中，一般情况下不区分这两个坐标系。

图1坐标系转换流程图
Fig.1Coordinate Transformations

根据1976岁差模型和1980章动模型，岁差和章动矩阵如下：

P(t)=Rz(-ζA)Ry(θA)Rz(zA)，

(7)

N(t)=Rx(-εA)Rz(Δψ)Rx(εA+Δε).

(8)

地球自转矩阵为

R(t)=Rz(θGST).

(9)

极移矩阵为

W(t)=Ry(-xp)Rx(-yp).

(10)

天球地心赤道坐标系(J2000)到站心地平坐标系的转换为：

RITRF(xITRF,yITRF,zITRF)=[W]T[R]T[N]T[P]TRJ2K(xJ2K,yJ2K,zJ2K)，

(11)

RAZEL=Ry(φA-90°)Rz(θLST-180°)RITRF.

(12)

上述方程中，RITRF，RJ2K，RAZEL为空间物体分别在地固系、J2000平赤道坐标系和站心地平坐标系中的直角坐标；Rx(θ),Ry(θ),Rz(θ)为旋转矩阵，代表任一矢量分别绕x,y,z轴旋转θ角,逆时针为正。其中，θGST为格林尼治真恒星时；xp,yp为极移分量；φA为瞬时天文纬度；θLST为地方恒星时。(7)、 (8)式中ΔΨ,Δε为黄经章动和交角章动，其余参数均是与时间相关的参数。

理论赤经赤纬转换得到的方位角Ai′、高度角hi′与修正大气折射后轴系定位的观测值(Ai,hi)的残差，由(6)式可得到方位角与高度角的中误差。其中方位角的残差与赤经残差相似，需要乘高度角的余弦值，即用[Ai-Ai′]cosh表示。这样也得到了望远镜轴系定位的误差。

3　数据结果分析

图2是1号、2号设备分别观测41240卫星(JASON 3)时，天文定位中赤经与赤纬的残差。两台设备天文定位赤经、赤纬的残差均在几角秒之内，有某些残差较大的值，可能存在较大的随机误差，不影响系统误差的评估，可以忽略。

图2两台设备观测JASON 3卫星天文定位残差对比
Fig.2Residual analysis for celestial positioning of JASON 3 satellite observed by the two equipment

图3为两台设备分别观测41240卫星(JASON 3)时，轴系定位中方位角与高度角的残差。从图中可以看出，1号设备比2号设备的轴系定位误差大，1号设备方位角误差为106″，高度角误差为36″。2号设备方位角与高度角误差均为十几角秒。两台设备对其他相同目标的观测数据也进行相同处理，结果与41240卫星相似，在此不一一列举。

图3两台设备观测JASON 3卫星轴系定位残差对比
Fig.3Residual analysis for axis positioning of JASON 3 satellite observed by the two equipment

从两台设备对相同目标进行观测的残差结果来看，两台设备的天文定位都具有较低的测量误差。并发现轴系定位方面，1号设备可能存在较大问题，尤其是方位轴。为了进一步确定此推论，对两台设备不同目标的观测数据也进行了误差分析，得到的测量误差(残差中误差)如表3、表4。

表3　1号设备观测不同目标的测量误差Table3　No.1equipment′serrorsofdifferentobjects

表4　2号设备观测不同目标的测量误差Table4　No.2equipment′serrorsofdifferentobjects

从表3与表4的对比可以看出，两台设备在天文定位的误差相差不大，而轴系定位方面1号设备的误差高于2号设备，尤其是方位角误差达到上百角秒。初步推断1号设备轴系定位系统出现故障，需对比1号设备在国内的观测数据，确定故障出现的大致时间。1号设备在国内长春试验观测时，部分观测数据误差分析结果如表5。

表5　1号设备在长春的测量误差Table5　No.1equipment′serrorsofdifferentobjectsinChangchun

通过表5与表3、表4的对比，三者天文定位的误差均低于10″，且具有良好的稳定度。而2号设备的轴系定位误差与1号设备在国内长春的轴系定位误差相差不大，均为10″～20″，且有较好的稳定性，好于1号设备在伊朗时的轴系定位数十、上百角秒的测量误差。1号设备在国内的轴系定位测量误差只有十几角秒，与2号设备精度相当，可以认为在国内时1号设备轴系定位并没有问题。在国外测量误差增加及稳定性明显下降，说明此时1号设备出现了问题。随后伊朗观测站报告15 cm光电望远镜轴系定位系统方位轴出现了运转不灵的情况，证实了这一判断，也证明了本文所用的通过对比分析天文定位和轴系定位数据的测量误差与稳定性判断望远镜转台的工作状态可行有效。

4　总　结

尽管轴系定位的误差略高，但在天文定位工作良好的情况下，以天文定位误差作为参考量，通过综合分析轴系定位的观测误差及稳定性判断望远镜跟踪硬件的工作状态是否正常。在APOSOS项目1号、2号设备的空间目标定位中，天文定位观测误差一般小于10″，适合用于高精度空间目标探测。而轴系定位观测误差较大，且稳定度不高，测量误差在10″到100″不等，可作为天文定位的辅助观测。且1号设备在伊朗时的轴系定位存在较大误差，在国内观测时没有发现同样问题，明确了是在伊朗观测时出了问题，随后伊朗观测站的报告也证实了这一结论，验证了分析方法的可行性和有效性。利用本方法可指导设备故障排查的方向，有助于快速诊断与维修，不仅解决了APOSOS项目望远镜的动态监测问题，对于无法现场检测的远程控制站点和无人值守望远镜也有重要的参考价值。

致谢：感谢提供实际观测数据的各观测站，感谢他们的工作与支持。

参考文献：

[1]李语强, 李荣旺, 李祝莲, 等. 空间碎片激光测距应用研究[J]. 红外与激光工程, 2015, 44(11): 3324-3329.

Li Yuqiang, Li Rongwang, Li Zhuliang, et al. Application research on space debris laser ranging[J]. Infrared and Laser Engineering, 2015, 44(11): 3324-3329.

[2]汤儒峰, 李语强, 李荣旺. GEO暗弱空间碎片目标搜索策略分析[J]. 天文研究与技术, 2017, 14(3): 304-309.

Tang Rufeng, Li Yuqiang, Li Rongwang. The strategic analysis for searching faint space debris in the GEO region[J]. Astronomical Research & Technology, 2017, 14(3): 304-309.

[3]祁先锋. 空间碎片观测综述[J]. 中国航天, 2005(7): 24-26.

[4]高鹏骐, 赵有, 张伟, 等. 亚太地基光学空间物体观测系统项目进展与展望[C]// 第七届空间碎片会议论文集. 2013.

[5]吴连大. 人造卫星与空间碎片的轨道和探测[M]. 北京: 中国科学技术出版社, 2011.

[6]李振伟, 张涛, 孙明国. 星空背景下空间目标的快速识别与精密定位[J]. 光学精密工程, 2015, 23(2): 589-599.

Li Zhenwei, Zhang Tao, Sun Mingguo. Fast recognition and precise orientation of space objects in star background[J]. Optics and Precision Engineering, 2015, 23(2): 589-599.

[7]李振伟, 杨文波, 张楠. 水平式光电望远镜静态指向误差的修正[J]. 中国光学, 2015, 8(2): 263-269.

Li Zhenwei, Yang Wenbo, Zhang Nan. Static pointing error of level mounting optoelectronic telescope[J]. Chinese Optics, 2015, 8(2): 263-269.

[8]陈艳玲, 黄勇, 胡小工, 等. CCD测角与激光测距技术综合测定空间目标的轨道[J]. 中国科学院上海天文台年刊, 2014(35): 112-121.

Chen Yanling, Huang Yong, Hu Xiaogong, et al. Space target′s orbit determination using CCD and SLR techniques[J]. Annals of Shanghai Astronominal Observatory, CAS, 2014(35): 112-121.

[9]于欢欢, 高鹏骐, 沈鸣, 等. 空间碎片激光测距探测能力分析[J]. 天文研究与技术, 2016, 13(4): 416-421.

Yu Huanhuan, Gao Pengqi, Shen Ming, et al. Detection capability analysis of space debris laser ranging[J]. Astronomical Research & Technology, 2016, 13(4): 416-421.

[10]孙明国, 刘承志, 范存波, 等. 基于SLR精密轨道的天文定位精度分析[J]. 天文学报, 2012, 53(2): 153-160.

Sun Mingguo, Liu Chengzhi, Fan Cunbo, et al. Analysis on the accuracy of celestial positioning based on SLR precise orbit[J]. Acta Astronomica Sinica, 2012, 53(2): 153-160.