基于Demons配准的NVST太阳高分辨 图像横向速度场测量*

刘　辉，杨云飞，尚振宏，李润鑫

(1. 昆明理工大学信息工程与自动化学院，云南 昆明 650500; 2. 昆明理工大学云南省计算机技术应用重点实验室，云南 昆明 650500)

太阳观测已经全面进入高空间和高时间分辨率的时代。以日本HINODE卫星[1]、中国1 m新真空太阳望远镜(New Vacuum Solar Telescope，NVST)[2]、美国Goode Solar Telescope[3]和瑞典Swedish Solar Telescope[4]为代表的高分辨望远镜已经产生了海量的多波段观测序列资料，为太阳物理的研究带来重要的机遇和挑战[5]。这些资料直观地从强度上展现了太阳大气中时刻发生的各种尺度的活动现象(太阳风暴、大小尺度活动以及存在于各种尺度中的磁流体动力学波和震荡)的细节及变化情况。高时空分辨率的图像不但能从形态上展示太阳大气的强度变化，同时也为量化分析和定量描述带来了可能。其中，通过强度像随着时间的变化计算这些活动的横向速度场已被广泛应用于太阳光球、色球表面特征的动力学分析。

太阳光球和色球的横向运动速度的典型值在每秒几千米到几十千米。对于目前的高分辨太阳图像序列的空间分辨率和时间分辨率，这意味着要精确测量图像两帧之间亚像素级或者几个像素级的位移量。在太阳图像的数据处理领域，这方面已经有了很多的发展。最为经典的有局部相关跟踪法(Local Correlation Tracking, LCT)[6]以及后来的基于傅里叶变换的局部相关跟踪法(Fourier Local Correlation Tracking, FLCT)[7]。微分仿射速度估计(Differential Affine velocity estimator, DAVE)[8-9]等技术在引入磁场感应方程后，首先被用于磁图非势性研究，然后被应用于强度像的测量[10-11]。此外文[12-13]提出了一种Balltracking方法，用于光球超米粒结构的研究。虽然这些方法都得到了一些很好的结果，但在测量精度上还不能匹配1 m太阳望远镜这种像元分辨率在0.05 arcsec、时间分辨率高达十多秒的高分辨图像处理要求，因而有必要对相关方法进行更为深入的研究。

横向速度场的测量实际上是通过测量一定时间间隔的两帧图像之间特征的位移量。由于太阳序列图像是某种 “光” 强度随着时间的变化，因此速度场是一种典型的光流场。从另外一方面，两帧图像之间的位移测量也可以看作是一种图像非刚性的配准。而随着计算机图像处理技术的发展，光流场的测量和图像非刚性配准技术已经有了非常大的发展。

图像非刚性配准方法可以由3部分描述：(1)联系源图像和目标图像的空间变换；(2)测量目标图像和源图像相似性的相似性测度；(3)决定最优变换参数的优化方法。

非刚性配准方法主要有基于空间变换的配准方法和基于物理模型的配准方法两大类。其中，由文[14]提出的基于热力学中流体扩散理论的Demons非刚性配准方法具有处理非光滑变形、抗噪声性能好等优点，被广泛应用于医学图像配准[15]，也非常符合太阳光球和色球层的磁流体非均匀局部变形的物理特性。

本文用Demons方法测量1 m太阳望远镜高分辨光球和色球观测数据的横向速度场。测量结果表明该方法可以较为精确地测量太阳高分辨图像的横向速度场，优于传统的基于傅里叶变换的局部相关跟踪法和微分仿射速度估计方法。

1　Demons方法

1.1　Demons 配准的原理和流程

经典Demons算法由Thirion提出，即 “Demons-base” 算法[14]。在概念上，它和19世纪麦克斯韦(Maxwell)的实验原理很相似。该算法的基本思想是假设运动目标的灰度不随时间改变，那么非刚性配准可以看作是浮动图像中各个像素向参考图像逐步扩散的过程，浮动图像各个像素的扩散速度由参考图像的灰度梯度信息决定。假设参考图像r、浮动图像f都是图像函数I[x(t),y(t),t]在某一时刻的 “快照”，图像函数的灰度值保持常数，则此假设可被模型化为

I[x(t),y(t),t]=c,

(1)

f=I[x(t0),y(t0),t0],

(2)

r=I[x(t1),y(t1),t1].

(3)

在初始时刻t0，图像函数I等于f，经过一定时间到达t1时刻后，图像函数被完全变形为r。图像配准的过程就是要得出一个能驱动f中的各个像素点向r中对应像素点移动的向量场。为了得出驱动力，将(1)式偏微分，得到：

(4)

(4)式可以简化为

v·r=f-r,

(5)

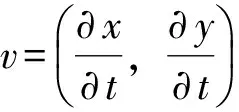
(6)

若将浮动图像的梯度信息作为一种正内力，参考图像的梯度信息作为负内力，利用这两种力同时驱动形变，得到的扩散速度为

(7)

Demons算法利用图像局部信息驱动形变，在全局范围内使形变连续，从而保证图像的拓扑结构。

1.2　基于梯度互信息的Demons方法

在Demons模型中，浮动图像各个像素都可以自由移动，使得在浮动图像中具有某个特定灰度值的所有像素有可能映射到参考图像上的同一像素点，导致错误的配准结果，为了使图像像素能够沿着正确的方向移动，在(7)式的基础上，采用梯度互信息进一步改进Demons算法，在原有扩散速度的基础上，增加了两幅图像之间梯度互信息的作用，使两幅图像配准结束的同时梯度互信息也达到最大。改进后的Demons算法扩散速度模型为

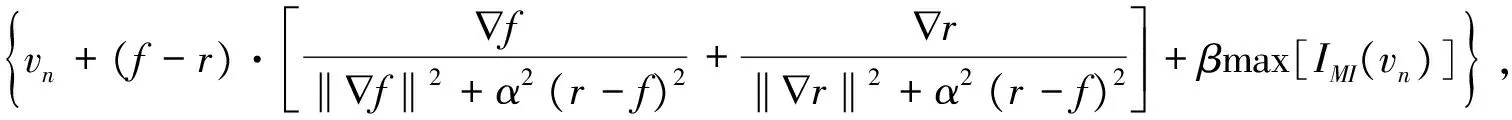
(8)

其中，max[IMI(vn)]为两幅图像的梯度互信息；β为正常数，表示此项的权重。

基于图像灰度互信息的配准方法，最大的不足是忽略了图像的空间信息。就太阳图像配准过程而言，对相同目标所成图像可能具有不同的灰度、不同的分辨率，甚至图像本身大小也不同，但是对于同一目标，其边界是确定的，不会发生很明显的变化；当两幅图像配准时，对应位置像素点的梯度矢量将具有相同或者相反的指向。基于以上分析，梯度互信息采用Parzen窗方法进行计算。

2　实验数据

1 m太阳望远镜作为中国最大的太阳望远镜和世界三大高分辨成像太阳望远镜之一，其优良的观测性能和高质量的图像已经在很多方面得以证实。为检验Demons方法的可用性，选取了具有代表性的3个1 m太阳望远镜观测资料数据集，包括两组光球图像和一组色球图像，每组图像为前后两帧。通过计算这两帧图像的光流场或者对它们进行非刚性配准，可得到相应的速度场。

数据集1包括的两帧图像均为1 m太阳望远镜在TiO波段观测的光球Level 1 + 重建像，观测时间为2013年11月3日04时58分31秒(UT)和05时01分28秒(UT)，时间间隔2分57秒。视场大小为685 × 650像元，像元分辨率为0.04 arcsec。光球上典型的1 km/s的横向速度将带来约6像元的位移。意味着整体光流场是超像素运动。

数据集2与数据集1是同目标、同波段、同期的观测，只是第1帧图像的观测时间为05时1分10秒(UT)，与第2帧相隔仅18秒，大约是数据集1的1/10，其他参数与数据集1相同。这样1 km/s的横向速度将带来仅仅0.6像元的位移，即光流场为亚像素运动。

数据集3的两帧图像为1 m太阳望远镜在Hα波段的Level 1 + 重建像。观测时间为2017年8月6日09时59分53秒和10时00分25秒，时间间隔为32秒。视场大小为238 × 225像元，像元分辨率0.13 arcsec。色球上5 km/s的横向速度带来约1.7像元的位移，总体光流场中包括亚像素和超像素的位移。

从图1可以看到，光球像数据集1和2是一个太阳活动区的局部，特征结构覆盖了米粒、黑子本影和半影。数据集3是典型的色球纤维，图像结构本身就有很强的自相似性。

图1(a)数据集1和2中的第2帧；(b)数据集3中的第2帧
Fig.1The second frame of dataset 1 and 2 (a) and the second frame of dataset 3 (b)

3　数据处理结果

对上述3个数据集采用Demons方法计算第2帧相对于第1帧的逐像素位移量，即光流场，然后根据相应的时间间隔归算到逐点的横向速度场。图2显示了数据集1中一个小区域的两帧图以及用Demons方法计算出的位移矢量。米粒的细微运动可以清晰地反映在图上。

图2数据集1中同一区域的变化及用Demons方法测量到的矢量场
Fig.2The same region of two frames in dataset 1 and the vector fields measured by Demons

为了测试Demons的结果并与目前太阳观测资料处理中常用的基于傅里叶变换的局部相关跟踪法和微分仿射速度估计方法进行比对，在分别采用不同方法得到光流场后，采用双线性插值将第2帧与第1帧进行非刚性配准，并利用图像结构相似度指数(Structural Similarity Index Measurement, SSIM)[16]测试配准的精度。较高的配准精度即意味着较高的光流场(速度场)测量精度。

对于x，y两张图像，其图像结构相似度指数由下式求得：

(9)

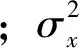
为了逐像素比对非刚性配准后的两帧图像的相似度，采用11 × 11像素邻域的窗口平均作为该点的局部图像结构相似度指数值。对于配准的结果，如果有更多点的图像结构相似度指数值接近1，说明该方法总体位移测量更为准确，配准更好。而图像中所有像素点图像结构相似度指数值的平均作为两帧图像的平均相似度值，也代表整体测量水平。

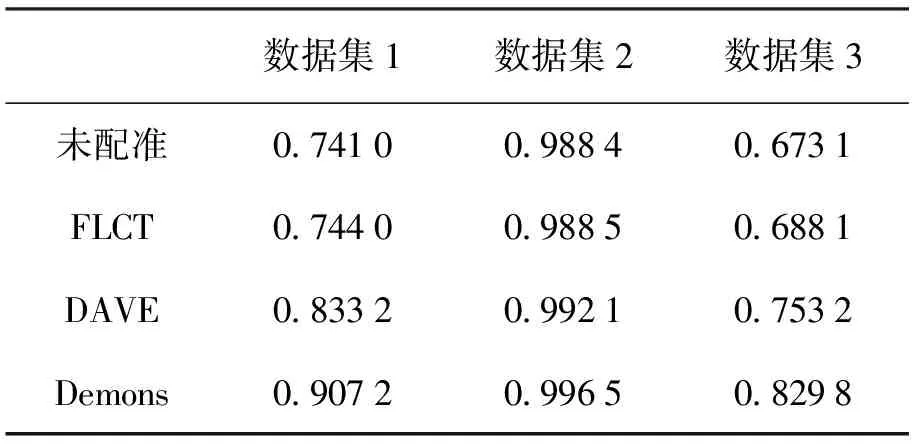
表1给出了3个数据集在未配准前和使用基于傅里叶变换的局部相关跟踪法、微分仿射速度估计和Demons方法分别测量并非刚性配准后与第1帧图像比较的平均图像结构相似度指数值。

从表1可以看出，原始数据彼此的相似度不但取决于时间间隔，也取决于特征结构的运动速度。对于色球数据，快速的运动导致在半分钟内图像就有较大的变化。另外，使用基于傅里叶变换的局部相关跟踪法配准后，图像结构相似度指数提升非常有限，即只测量到很少的运动。再则，微分仿射速度估计方法的测量结果有显著的提升，但Demons方法更优。

表1不同方法配准后的平均图像结构相似度指数值

Table1TheSSIMindexafternon-rigidregistrationwithdifferentmethod

数据集1数据集2数据集3未配准074100988406731FLCT074400988506881DAVE083320992107532Demons090720996508298

数据集1间隔时间较长，而数据集3的色球运动较快。在这两个数据集中，特征结构除了局部的运动外，还有新结构的浮现和旧结构的消失，因此图像结构相似度指数相对偏小。而数据集2中两帧图像时间间隔仅为18 s，且光球运动较为缓慢，图像差异微小，图像结构相似度指数也明显高于其他两个数据集。但无论原始图像情况如何，Demons方法对于不同的数据集均表现出良好的处理能力。

图3显示了对数据集1应用3种方法配准后的逐点图像结构相似度指数的直方图概率分布。可以看到Demons方法配准后图像结构相似度指数值的整体分布更靠近1，明显好于微分仿射速度估计和基于傅里叶变换的局部相关跟踪法。同时基于傅里叶变换的局部相关跟踪法的结果和未配准图像非常接近，即测量效果并不显著。这与表1的结果是一致的。数据集2和3的图像结构相似度指数概率分布也反映出同样的趋势。

从最终速度场的测量情况看，3个数据集都呈现同样的趋势： 基于傅里叶变换的局部相关跟踪法基本上只能在位移较大的情况下有测量值，而微分仿射速度估计的测量值系统性小于Demons的测量值，大多数情况只有Demons方法测量精度的一半。

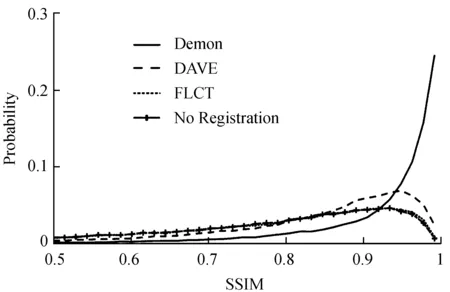
图3数据集1的不同方法配准后的逐点图像 结构相似度指数概率分布

Fig.3The probability distribution of SSIM index with different registration method applying dataset 1

4　模拟数据测试

Demons方法虽然结果好于微分仿射速度估计和基于傅里叶变换的局部相关跟踪法，但第2帧经过非刚性配准后也并没有做到完全匹配，即图像结构相似度指数并不等于1。其中最为重要的原因无论是光球还是色球，经过一段时间间隔后，不但原有的米粒、黑子或者色球纤维产生位移，同时也有新特征的产生和旧结构的消失，这不是仅从光流场能够计算的。

为了进一步比较Demons和微分仿射速度估计的光流场测量精度，测试他们在不同太阳图像(光球和色球)上亚像素和超像素位移的可靠性，设计了两个模拟实验，即分别将数据集1和数据集3中的第1帧图像在X和Y方向整体移动一个固定量，从而产生第2帧刚性运动的图像，然后分别再用两个方法测量其与第1帧图像的光流场。由于模拟的是全局性位移，因此其逐点光流场的均值和标准差即可以很好地反映测量的精度。

表2给出了整体位移为(5.7, -0.2)时，这两个方法在X和Y方向上测量的统计结果。

表2　模拟数据使用微分仿射速度估计和Demons方法测量的统计结果Table2　ThestatisticsresultsofDAVEandDemonsforsimulationdata

可以看到，与预设值相比，Demons的均值和标准差表现都明显好于微分仿射速度估计方法，逐点测量精度在0.1像素。而微分仿射速度估计不但标准差比Demons方法高一个量级，而且均值也有较大的系统偏差，尤其对于自相关较强的色球图像。一般认为微分仿射速度估计在做超像素测量时误差较大，但测试结果表明微分仿射速度估计受到图像本身的特征结构的影响也很大。这与微分仿射速度估计本质上也是使用相关方法测量有关。基于傅里叶变换的局部相关跟踪法由于能计算的像素太少，缺乏统计意义，因此被排除在外。

同时，由于是模拟整图的刚性位移，因此也可以用标准的整幅图像互相关方法直接测量两组图像的刚性位移。光球像的测量结果为(5.757 8, -0.181 4)，而色球像的结果为(5.744 6， -0.065 4)，也比用Demons方法逐点测量后的均值结果明显偏差要大。这意味着Demons方法不但适用于非刚性的配准，同时也可以利用均值测量图像刚性的位移，用于图像的刚性配准。尤其对于自相似性较强的目标，如色球纤维、太阳边缘等，这一方法有较强的优势。

5　结　论

本文详细描述了Demons方法，并利用其测量不同目标和不同位移量的太阳高分辨像的横向速度场。对测量结果进行图像非刚性配准后，图像结构相似度指数有了明显的提高，从而说明位移的测量更为准确，表明这一方法的可行性。通过与微分仿射速度估计和基于傅里叶变换的局部相关跟踪法进行对比，Demons方法表现出较为明显的优势。而光球和色球数据的亚像素和超像素模拟位移实验表明，Demons逐点测量精度在0.1像素量级。这意味着在1 m太阳望远镜18 s间隔的光球像上可以得到200 m/s精度的横向速度，而在32 s的色球像上可以得到500 m/s的速度精度。另外，对于图像结构自相关性较大的图像配准，这一方法无论在非刚性和刚性配准方面相对于传统互相关方法有明显的优势。

对比研究同时也表明，基于傅里叶变换的局部相关跟踪法基本不适合测量高分辨像，而微分仿射速度估计直接用于强度像的测量也难以得到精确的结果。

Demons方法在亚像素和超像素测量上都能获得较高的精度，但是由于其算法的复杂性，使得计算机开销较大，计算时间较长，并不太适合大尺寸高分辨图像的整体运算。同时处理的图像有较为明显的边界效应，因此在实际处理时，需要对关注的区域做一定的边缘扩展。

必须指出的是，这种利用光流场测量横向速度场从本质上是假设物质的运动表现为图像强度的横向变化，而且这也仅仅是在观测平面上的投影，并不是真正的物质流动方向。同时如果有新图像结构的产生和旧结构的消失，从本质上这种测量方式是有缺陷的，因此需要高时间分辨率的观测，以减少这种变化。但更短的时间间隔意味着更小的位移量。

理论上，这一方法可以用于处理其他望远镜的高分辨观测图像，也可以用于一些低分辨数据，或者其他类型的图像上，这些还需要进一步尝试。

致谢：感谢中国科学院云南天文台澄江观测站和1 m太阳望远镜全体人员对论文工作的大力支持和帮助。

参考文献：

[1]Tsuneta S, Ichimoto K, Katsukawa Y, et al. The Solar Optical Telescope for the Hinode mission: an overview[J]. Solar Physics, 2008, 249(2): 167-196.

[2]Liu Z, Xu J, Gu B Z, et al. New vacuum solar telescope and observations with high resolution[J]. Research in Astronomy and Astrophysics, 2014, 14(6): 705-718.

[3]Goode P R, Denker C J, Didkovsky L I, et al. 1.6 M solar telescope in Big Bear-the NST[J]. Journal of the Korean Astronomical Society, 2003, 36(S1): S125-S133.

[4]Scharmer G B, Bjelksjo K, Korhonen T K, et al. The 1-meter Swedish solar telescope[C]// Proceedings of SPIE. 2002: 341-350.

[5]汪景琇, 季海生. 空间天气驱动源—太阳风暴研究 [J]. 中国科学: 地球科学, 2013, 43(6): 883-911.

Wang Jingxiu, Ji Haisheng. Space weather driving Source-solar storm research[J]. Scientia Sinica Terrae, 2013, 43(6): 883-911.

[6]November L J, Simon G W. Precise proper-motion measurement of solar granulation[J]. The Astrophysical Journal, 1988, 333: 427-442.

[7]Fisher G H, Welsch B T. FLCT: a fast, efficient method for performing local correlation tracking[C]// Subsurface and Atmospheric Influences on Solar Activity ASP Conference Series. 2008: 383.

[8]Schuck P W. Local correlation tracking and the magnetic induction equation[J]. The Astrophysical Journal, 2005, 632(1): L53-L56.

[9]Schuck P W, Chen J. Tracking magnetic footpoints with the magnetic induction equation[J]. The Astrophysical Journal, 2006, 646(2): 1358-1391.

[10]Wang S, Liu C, Deng N, et al. Sudden photospheric motion and sunspot rotation associated with the X2.2 flare on 2011 February 15[J]. Astrophysical Journal Letters, 2014, 782(2): L31-L36.

[11]Liu C, Xu Y, Cao W, et al. Flare differentially rotates sunspot on Sun′s surface[J]. Nature Communications, 2016, 7: 13104.

[12]Potts H E, Barrett R K, Diver D A. Balltracking: an highly efficient method for tracking flow fields[J]. Astronomy & Astrophysics, 2004, 424(1): 253-262.

[13]Potts H E, Diver D A. Automatic recognition and characterisation of supergranular cells from photospheric velocity fields[J]. Solar Physics, 2008, 248(2): 263-275.

[14]Thirion J P. Image matching as a diffusion process: an analogy with Maxwell′s demons[J]. Medical Image Analysis, 1998, 2(3): 243-260.

[15]Kroon D J, Slump C H. MRI modality transformation in demon registration[C]// Proceedings of the IEEE International Symposium on Biomedical Imaging. 2009: 963-966.

[16]Wang Z, Bovik A C, Sheikh H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612.