基于故障传播的模块化BP神经网络电路故障诊断
2018-04-12吴让好刘邦欣
何 春,李 琦,吴让好,刘邦欣
(电子科技大学 通信与信息工程学院,成都 610054)(*通信作者电子邮箱1287345989@qq.com)
0 引言
近年来,随着数模混合电路规模和复杂性的增加,特别是在航空、航天、军事国防等应用领域,其可靠性受到越来越多的关注。故障诊断作为维护电路可靠性的重要手段,成为了研究热点。文献[1-4]中提到的电路故障诊断方法包括:故障字典、最近邻、基于规则和支持向量机(Support Vector Machine, SVM)的故障分类模型等,但仅在模拟电路中付诸实践,且由于复杂电路的非线性映射关系错综复杂,导致诊断效果不佳。BP(Back Propagation)神经网络在数学理论上已证明具有实现绝大多数复杂非线性映射的功能,这使得它对诊断实际中建模困难的复杂系统,特别是大规模混合电路,具有独特优势。
传统BP神经网络的应用[5-9]是直接对整个电路建立BP网络,建立该网络的过程简单明了,适用于简单线性电路的故障诊断。在对大规模电路进行分析时,所建立的网络过大,易导致训练数据庞大、训练时间过长、计算量大以及对故障传播考虑欠缺等问题,从而造成故障定位准确率低。本文提出了基于故障传播的模块化BP神经网络(Modularized BP neural network based on Fault Propagation, MBPFP)故障定位方法,对大规模电路进行模块划分,分析并“分割”子电路模块间的故障传播关系,进而利用基于电路仿真建立的模块化异常检测模型和BP神经网络模型进行故障定位,使定位的准确率得到明显提升。
1 MBPFP的故障诊断原理
大规模数模混合电路结构复杂,输入输出关系难以用简单的数学公式表示,电路故障状态庞杂,传播关系错综复杂。MBPFP方法在电路模块化的基础上,通过最优测试节点的选择确定子电路模块的测试节点,并把测试节点的属性数据作为故障诊断的数据源,使复杂电路的故障表现形式具体化;以电路单故障仿真[10]的测试节点属性数据为客观依据,建立模块化异常检测模型,分析故障传播并“分割”故障传播关系,建立子电路的BP神经网络模型,确定电路故障与故障原因的内在联系;当实际电路发生故障时,利用模块化异常检测模型进行一级定位,确定故障模块,再利用目标模块的BP神经网络模型进行二级定位,识别故障模式[10]。下面对MBPFP中的关键技术进行详细介绍。
1.1 模块化电路测试节点的确定
大规模电路的可测节点众多,造成数据采集、传输和处理的负荷过大,因此首先进行电路模块划分,并确定各子电路模块的测试节点。本文采用电路按功能划分的方法,尽可能地简化子电路模块间的拓扑关系和参数之间的耦合。为了避免因分析所有可测节点带来的冗余问题,同时兼顾一级定位的故障覆盖率,在功能模块划分的基础上,通过最优测试节点的选择确定各模块的测试节点。
最优测试节点的选择是将传统的包含法和排除法[11-12]相结合,从可测节点集合中生成节点子集,并评价其性能,选择性能最佳的节点子集作为最优测试节点。节点子集性能的评价标准为故障覆盖率,公式如下:
Coverage=|A|/|D|
(1)
其中:Coverage表示故障覆盖率;|D|表示待检测的故障总数;|A|表示可以被检测到的故障数。考虑到工程实际,最终选定的最优测试节点集要覆盖各子电路模块的输出节点。
最优测试节点的选择算法具体如下:
令OrigNodeSet是可测节点集合
令OutNodeSet是子电路模块输出节点集合
令OptiNodeSet={}是最优测试节点的初始集合
令best_Coverage=0是最佳的初步定位故障覆盖率,初始值为0
%%包含法
令NodeSet_Reg={}寄存包含法选择出的节点
for 每个可测节点Node∨OrigNodeSetdo
NodeSet=Node∨NodeSet_Reg
%%Coverage_Cal(*)以*节点的属性数据为输入,利用式(1)计算故障覆盖率
Coverage← Coverage_Cal(NodeSet)
ifCoverage>best_Coveragedo
best_Coverage=Coverage
追加Node至NodeSet_Reg的尾部:
NodeSet_Reg=Node∨NodeSet_Reg
end if
end for
%%排除法
OptiNodeSet=NodeSet_Reg
fori=1:(length(NodeSet_Reg)-1) do
forj=0:(length(NodeSet_Reg)-i-1) do
Node=NodeSet_Reg(end-i-j)
NodeSet=OptiNodeSet-Node
Coverage← Coverage_Cal(NodeSet)
ifCoverage==best_Coveragedo
OptiNodeSet=OptiNodeSet-Node
end if
end for
end for
%%与工程实际结合
for 每个可测节点Node∨OutNodeSetdo
if isempty(find(OptiNodeSet,Node)) do
OptiNodeSet=OptiNodeSet∨Node
end if
end for
returnOptiNodeSet
通过最优测试节点的选择,构造如下测试节点矩阵:
TestNodeMatrix=[aij]N×M; 1≤i≤N&& 1≤j≤M
(2)
其中:N表示子电路模块数;M表示可测节点数;aij表示可测节点Nodej是否为模块Modulei的最优测试节点(或测试节点),取值如式(3)所示。

(3)
以TestNodeMatrix为基础,获取相应节点的属性数据,建立模块化异常检测模型。
1.2 模块化异常检测模型
在电路故障诊断中,异常检测[13]的目标是发现与正常电路有差别的故障电路。当大规模电路故障时,故障情况复杂,故障原因众多,利用异常检测模型监测电路、筛选并缩小故障原因集合是一种有效手段。
本文通过电路单故障仿真得到各测试节点的“与正常波形的距离”属性[10]数据,且由于同节点同属性的数据近似地呈高斯分布[14],因此根据文献[15],通过参数法的密度估计法建立各测试节点的一元高斯分布异常检测模型(pij(xij),εij),(pij(xij),εij)表示子电路Modulei(1≤i≤N)中第j(1≤j≤M)个测试节点的异常检测模型如下:

(4)
其中:
(5)
其中:xij表示节点的“与正常波形的距离”属性样本;εij表示模型的概率阈值;ONormal表示正常样本集合;OAnomaly表示故障样本集合。
测试节点的异常检测模型利用概率pij(xij)和概率阈值εij对节点的故障状态进行评估,阈值εij不是固定的,可以随训练数据的变化而自动调整,有别于传统的阈值判断方法,所以该模型是一种“阈值自动调节”的软性故障判别方式。
根据测试节点矩阵TestNodeMatrix,以测试节点的异常检测模型(pij(xij),εij)为基础,构建模块化异常检测模型(Anomaly Detection Model based on Module, ADMModule)。当子电路模块中只要有一个测试节点故障时,则模块表现故障,计算式如下:
ADMModule_i=
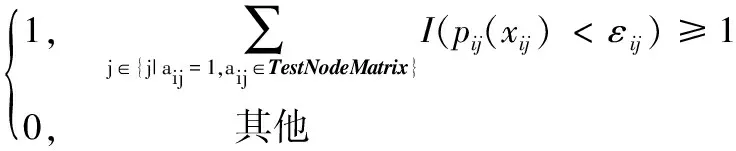
(6)
其中:ADMModule_i表示第i(1≤i≤N)个子电路模块的异常检测模型;I(*)表示指示函数,只有*成立时,I(*)=1。通过最优测试节点的选择确定各子电路的测试节点,使模块化异常检测模型在应用于一级定位时,故障覆盖率更佳。
将各子电路的模块化异常检测模型组合为如下向量形式,以便后续操作。
ADMVector=
[ADMModule_1ADMModule_2…ADMModule_t…ADMModule_N]
(7)
其中:ADMModule_t(1≤t≤N)在ADMVector中按照子电路模块物理连接先后的顺序排列(并联模块对应的ADMModule_t排序任意)。
1.3 基于子电路模块的故障传播分析
由于数模混合电路故障状态复杂,且电路模块划分并不能真正意义上作到“划分后的各子电路之间没有拓扑关系和参数之间的耦合”,所以模块间可能存在故障传播而相互影响,数模混合电路不仅存在故障正向传播,还存在故障反向传播,增加了故障定位的难度,因此,本文基于电路单故障仿真,利用模块化异常检测模型的向量形式ADMVector获取各故障模式的故障向量SFaultMode,并组合为失效矩阵FaultMatrix;再以FaultMatrix为数据源,利用有向图模型[16]分析各故障模式在子电路模块间的故障传播情况(只分析电路发生单一故障时的故障传播情况),将故障源和传播源“模块化”为某些子电路的故障来源。故障来源具体分两种:一是该模块内部的元器件故障模式(内部故障模式);二是与该模块存在直接或间接物理连接的模块中的元器件故障模式(外部故障模式)。
以故障模式为分析单元,通过电路单故障仿真获得所有测试节点“与正常波形的距离”属性数据,并利用ADMVector获得各故障模式的故障向量SFaultMode,如下:
SFaultMode_k=[s1s2…st…sN]
(8)
其中:SFaultMode_k表征第k个故障模式对各子电路模块的故障影响,1≤k≤L,L表示故障模式数;st表示利用ADMModule_t检测第t个子电路模块时,该模块的故障状态。st取值如下:

(9)
将所有故障模式的故障向量组合为失效矩阵FaultMatrix,如下:
FaultMatrix=[SFaultMode_1;SFaultMode_2;…;SFaultMode_k;…;
SFaultMode_L]=[bij]L×N;1≤i≤L&& 1≤j≤N
(10)
其中:L表示故障模式数;N表示子电路模块数。bij为FaultMatrix的元素,取值如下:
bij=sj;sj∈SFaultMode_i
(11)
以FaultMatrix为数据源,利用有向图分析故障传播,确定各模块的故障来源,如下:
FaultSourceModule_n=arg{m|bmn=1,bmn∈FaultMatrix}
(12)
其中:FaultSourceModule_n表示第n(1≤n≤N)个子电路模块的故障来源。根据SFaultMode,各子电路模块的故障来源具体可分为三种情况:
1)SFaultMode中的分量全为0时,则SFaultMode对应的故障模式不导致电路故障,为潜在故障模式;
2)SFaultMode中只有一个分量为1时,则SFaultMode对应的故障模式只使一个模块发生故障,不存在故障传播,是分量为1所表示的模块的故障来源;
3)SFaultMode中存在两个或多个分量为1时,则SFaultMode对应的故障模式使两个或多个模块发生故障,存在故障传播,是分量为1所表示的模块的故障来源。
通过基于子电路模块的故障传播分析,以FaultSourceModule为依据获取各子电路BP神经网络的训练数据,有机地将各子电路的异常检测模型和BP神经网络模型结合在一起。
电路Circuit1发生R3短路(以下简称R3_S_NULL)时的故障传播分析如下:首先将Circuit1模块划分为3个子电路并确定测试节点:S1为模块M1的测试节点;S2为模块M2测试节点;S3为模块M3的测试节点。电路模块划分和节点选择具体如图1所示。
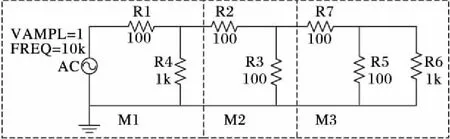
图1 电路Circuit1的模块划分Fig. 1 Module division of Circuit1
电路Circuit1正常工作状态下,节点S1、S2、S3的仿真结果如图2所示。

图2 电路Circuit1的正常仿真结果Fig. 2 Normal simulation results of Circuit1
当电阻R3短路时,节点S1、S2、S3的仿真结果如图3所示。

图3 R3短路时电路仿真结果Fig. 3 Simulation results of R3 shorting in Circuit1
由图2、3可知,当R3发生短路时,导致模块M2中节点S2输出为0,R3为M2的故障源;导致模块M1中节点S1输出幅值下降50 mV,R3(或其所在模块M2)为M1的故障反向传播源;导致模块M3中节点S3输出为0,R3(或其所在模块M2)为M3的正向故障传播源。所以R3短路故障对应的故障向量SR3_S_NULL=[1 1 1],基于子电路模块的故障传播有向图模型如图4所示。
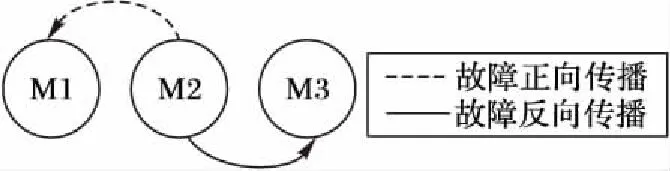
图4 R3短路的故障传播有向图模型Fig. 4 Fault propagation digraph model of R3 shorting
由图4表示的有向图故障传播模型可知,R3短路既是R3所在模块M2的故障源又是其他模块M1、M3的故障传播源。
1.4 模块化BP神经网络模型
BP神经网络[17]是人工神经网络的一种重要算法,包括无监督学习过程和有监督调优过程,通过学习和调优建立的分类模型具有较强的自学习能力。本文利用模块化异常检测模型只能在子电路层次进行故障诊断。为了提高定位精度,利用BP神经网络将故障原因集合缩小到故障模式。BP神经网络通过学习各种故障模式的样本数据自动提取“合理的”求解规则,建立BP网络模型,该模型保存了电路故障的内在因果对应关系,直接用于之后的二级定位。
为适应数模混合电路,根据测试节点信号的不同,建立属性表[10],如表1所示。

表1 电路测试节点信号的属性Tab. 1 Attributes of circuit test node signal
通过电路单故障仿真获取各测试节点的所有属性数据,并将其组合为一维属性向量进行最优属性选择,获得最优属性向量,再利用上述分析中各子电路模块故障时的故障来源FaultSourceModule筛选出各模块故障来源的最优属性向量,最终通过聚类构造各模块BP网络的训练样本集,建立模块化BP神经网络模型(BP neural network Model based on Module,BPMModule)。训练样本如下:
{[Att1Att2…Atti…AttK],index}
(13)
其中:Atti表示第i个最优属性,1≤i≤K,K表示最优属性的数量,[Att1Att2…Atti…AttK]作为BPMModule的输入数据;index表示故障模式经过聚类后的故障簇编号,用独热码表示,作为BPMModule的输出数据。所以该BPMModule为3层结构,输入层的节点数为最优属性的数量K,输出层的节点数为聚类所得的故障簇数,BP实质上实现了从故障属性输入到故障类别输出的映射功能。各子电路模块BP神经网络模型建立过程如图5所示。
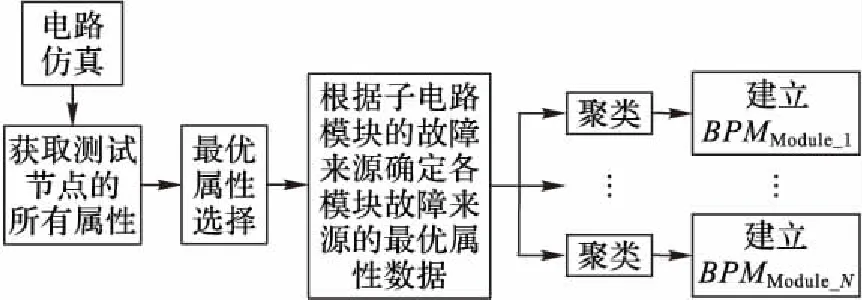
图5 各子电路模块BP神经网络模型建立示意图Fig. 5 Schematic diagram of establishing BP neural network model for subcircuit modules
将各子电路的模块化BP神经网络模型组合为如下向量形式,以便后续操作。
BPMVector=
[BPMModule_1BPMModule_2…BPMModule_t…BPMModule_N]
(14)
其中,BPMModule_t(1≤t≤N)在BPMVector中按照子电路模块物理连接先后的顺序排列(并联模块对应的BPMModule_t排序任意)。
1.4.1最优属性的选择
由各测试节点所有属性数据组成的一维属性向量显然会存在属性冗余问题,且不同属性在电路故障诊断中的重要程度不同,若将其直接聚类,建立BP神经网络模型,可能会因为属性之间的强相关性、冗余等问题,造成BP网络性能不佳甚至低下,因此,该一维属性向量需要通过最优属性选择去除冗余,再进行后续操作。
最优属性的选择是将一维属性向量中的属性按照性能的优劣排序,然后选择前K个性能最佳的属性作为最优属性。其中,有以下两点需要说明:
1)属性性能的评价是通过对将要用于的系统进行性能评估完成的,即利用DB Index[18]、相关性和故障簇数量对该属性的聚类效果进行评估。其中,DB Index评价聚类结果的凝聚程度,公式如下:

dij=‖Zi-Zj‖
(15)
其中:k表示聚类的簇总数;Si表示簇内平均离散度;|Ci|表示故障簇Ci中所包含的样本总数,Zi表示簇Ci的中心;dij表示簇间距离。对于DB Index准则来说,DBk值越小,说明聚类的效果越好。相关性评价参与聚类的各属性之间的冗余程度,公式如下:
(16)
其中:Atti表示参与聚类的第i个属性的数据。对于相关性来说,XCOR值越小,说明参与聚类的特征之间相关性越低,冗余程度越小。故障簇(故障模式集合)作为最终定位结果,故障簇数是对整个系统故障定位精确程度的评价,簇数越多,相应的每个簇中包含的故障模式数越少,定位精确程度越高。
2)最优属性数K的确定:完成最优属性的排序后,利用聚类的故障簇数确定K。K需要满足如下公式:

(17)
其中:l为任意正整数;OptiAttSet(*)表示前*个性能最佳的属性集合;NumOfCluster(*)表示*聚类的故障簇数。
最优属性的选择算法具体如下:
令OrigAttSet是属性向量
令OptiAttSet={}是最优属性的初始集合,初始为空
%%最优属性排序
令OptiAttSeq={}是最优属性排序的初始集合,初始为空
OrigAttSetReg=OrigAttSet
fori=1:length(OrigAttSet) do
DBReg={}
for 每个属性Att∈OrigAttSetRegdo
AttSet=Att∨OptiAttSeq
%%DB_Cal(*)以*属性的数据为输入,利用式(15)计算DB值
DB← DB_Cal(AttSet)
DBReg=DB∨DBReg
end for
AttReg1={arg(min(DBReg))}
ifi==1 do
AttReg2=AttReg1
else
XcorrReg={}
for 每个属性Att∈AttReg1 do
AttSet=Att∨OptiAttSeq
%%Xcorr_Cal(*)以*属性的数据为输入,利用式(16)计算相关值
Xcorr← Xcorr_Cal(AttSet)
XcorrReg=Xcorr∨XcorrReg
end for
AttReg2={arg(min(XcorrReg))}
end if
NumCluReg={}
for 每个属性Att∈AttReg2 do
AttSet=Att∨OptiAttSeq
%%NumOfCluster_Cal(*)以*属性的数据为输入,获得*属性聚类后的故障簇数
NumOfCluster← NumOfCluster_Cal(AttSet)
NumCluReg=NumOfCluster∨NumCluReg
end for
Att={arg(max(NumCluReg))}
追加Att到OptiAttSeq的尾部:
OptiAttSeq=Att∨OptiAttSeq
OrigAttSetReg=OrigAttSetReg-Att
end for
%%从OptiAttSeq中选择最优属性OptiAttSet
NCReg={}寄存不同个数的最优属性经聚类后的类故障数
fori=1:length(OptiAttSeq) do
AttSet=OptiAttSeq(1:i)
NumOfCluster← NumOfCluster_Cal(AttSet)
追加NumOfCluster到NCReg的尾部:
NCReg=NumOfCluster∨NCReg
end for
Dif_NCReg← diff(NCReg)
ind=find(Dif_NCReg==0)
OptiAttSet=OptiAttSeq(1:ind)
returnOptiAttSet
通过对测试节点的所有属性进行最优属性的选择,并将结果作为各模块BP神经网络模型的输入数据,使BP网络关于故障属性输入和故障类别输出间的映射关系更加全面合理,在二级定位时,定位准确率更高。
1.5 MBPFP的故障定位步骤
针对实际电路,建立相应的仿真电路,并通过仿真构建各子电路模块的异常检测模型和BP神经网络模型。当实际电路发生故障时(只考虑发生单一故障的情况),故障诊断过程如图6所示。
步骤1获取实际电路中各测试节点的电压,具体可通过在测试节点上安置电压感知器获取,并提取属性。
步骤2从各测试节点的属性中选取“与正常波形的距离”属性数据,利用模块化异常检测模型的向量形式ADMVector对各子电路的故障状态进行评估,获得实际故障向量Sactual=[s1s2…st…sN],Sactual与前文中提到的SFaultMode物理意义相同。

图6 实际定位过程示意图Fig. 6 Schematic diagram of actual positioning process
步骤3根据Sactual进行一级定位,缩小当前故障原因的搜索范围,结果如下:
1)Sactual中的分量全为0时,则电路正常。
2)Sactual中只有一个分量为1时,则电路故障,故障原因可以定位到如下模块:
FaultCause=arg({i|si=1})
(18)
即Sactual中为1的分量表示的模块。
3)Sactual中存在两个或多个分量为1时,则电路故障且模块间存在故障传播,但无法确定故障传播源。此时可分为如下两种情况:
情况1考虑到故障正向传播,选择如下模块作为一级定位的结果:
FaultCause=arg(min{i|si=1})
(19)
即Sactual中首个为1的分量对应的模块;
情况2考虑到故障反向传播,结果如下:
FaultCause=arg(max{i|si=1})
(20)
即Sactual中尾部为1的分量对应的模块。
若定位精度要求为子电路模块级,则定位结束;否则进行下一步。
步骤4根据一级定位的结果,从模块化BP神经网络模型的向量形式BPMVector中选择如下模型作为二级定位的诊断工具:
BPMTarget=BPMVector(FaultCause)
(21)
并从测试节点的属性值中筛选出最优属性数据,利用BPMTarget进行二级定位,将结果定位到故障模式。
2 实例诊断分析
将MBPFP方法应用于实际电路的故障诊断中,实例分析的仿真平台为OrCAD Capture 16.5和PSpice AD,数据处理平台为Matlab R2012b。
2.1 实例1
截取于某大型系统的时钟产生电路作为待诊断电路,如图7所示。图7电路包含56个故障模式,表2描述了电容C12、电阻R12和数字器件D3的部分故障模式。

图7 实例电路Fig. 7 Example circuit

表2 部分故障模式Tab. 2 Part of fault modes
利用PSpice AD进行电路正常仿真和单故障仿真。将电阻和电容的容差设为5%,对正常电路作200 000次蒙特卡罗(Monte Carlo,MC)分析,每种故障模式作100次MC分析,并根据表1提取MC样本所有可测节点的属性数据。取每种故障模式第一次MC对应的属性数据作为额定值训练样本集(Nominal Train sample SET, NTSET);取200 000组正常属性样本和每种故障模式中前80组属性样本作为容差值训练样本集(Tolerant Train sample SET, TTSET);取每种故障模式另外的20组样本作为测试样本集(TEST sample SET, TESTSET)。故障诊断过程具体如下。
步骤1将该电路按功能划分为4个模块:
ModuleInCircuit={FilterModule,CompareModule1,
CompareModule2,Counter16Module}
各子电路所含的可测节点依次如下:
NodeInModule={{S1,S2,S3},{S5},{S4,S6,S7},
{S8,S9}}
步骤2利用TTSET中的“与正常波形的距离”属性数据建立所有可测节点的异常检测模型。根据最优测试节点选择算法,结合式(6)和式(1),确定测试节点矩阵,同时可获得各子电路的模块化异常检测模型,矩阵如下:
矩阵中各行依次表示ModuleInCircuit中的各子电路模块所含的最优测试节点;各列依次表示NodeInModule中的各可测节点作为最优测试节点(或测试节点)时的归属模块。例如,a13=1表示S3为FilterModule的最优测试节点。根据TestNodeMatrix建立的模块化异常检测模型使一级定位的故障覆盖率理论上达到:
Coverage=|A|/|D|=56/56=100.00%
步骤3将步骤2中的模块化异常检测模型组合为向量形式,如下:
ADMVector=
[ADMFilterModuleADMCompareModule1ADMCompareModule2ADMCounter16Module]
步骤4基于NTSET,利用ADMVector建立各故障模式的故障向量SFaultMode。将表2中故障模式对应的故障向量组成的失效矩阵如下:

其中,各行依次表示表2中的各故障模式对各子电路模块的故障影响;各列依次表示ModuleInCircuit中的各子电路模块在各种故障模式下的故障状态。
步骤5以FaultMatrix为数据源,分析故障传播,并确定各子电路模块的故障来源FaultSourceModule,如下:
FaultSourceFilterModule=[C12_S_NULL,C12_F_UP,
R12_O_NULL,R12_F_DOWN,…]
FaultSourceCompareModule1=[C12_S_NULL,C12_F_UP,
D3_OZ_11,D3_H_11,…]
FaultSourceCompareModule2=[C12_S_NULL,R12_O_NULL,
R12_F_DOWN,D3_OZ_11,…]
FaultSourceCounter16Module=[C12_S_NULL,C12_F_UP,
D3_OZ_11,D3_H_11,…]
步骤6将NTSET中各测试节点的所有属性数据组合为一维属性向量,进行最优属性的选择,选择结果及性能数据如表3所示。

表3 最优属性Tab. 3 Optimal attributes
根据FaultSourceModule,筛选出各模块故障来源的最优属性向量,并通过聚类搭建各模块BP网络的训练数据框架。基于该框架,在TTSET中构建各BP网络的训练数据,训练精度设为0.01,建立各子电路的BP神经网络模型,其向量形式如下:
BPMVector=
[BPMFilterModuleBPMCompareModule1BPMCompareModule2BPMCounter16Module]
步骤7诊断。利用TESTSET对该方法进行测试,根据一级定位中故障传播分析方向的不同,分为如下两种情况:1)一级定位产生的故障向量按正向传播分析;2)一级定位产生的故障向量按反向传播分析。两种不同分析方向的性能如表4所示。

表4 MBPFP性能 %Tab. 4 Performance of MBPFP %
其中,定位准确率表示定位结果正确的样本数与所有样本数的比例。不管一级定位采用哪种故障传播分析方向,MBPFP的故障覆盖率和定位准确率在所设容差范围内性能均较好;另外,该方法有效地减小了各模块BP神经网络的计算量和训练时间,提高了故障定位线下训练的效率。
2.2 性能对比分析
文献[9]提出了一种大规模电路故障诊断神经网络方法,在电路模块划分的基础上,直接利用所有可测节点的电压值建立各子电路的BP神经网络,再利用各BP神经网络依次进行故障定位,没有涉及测试节点的选择、属性选择,也没有考虑到存在故障传播的情况。
文献[15]提出了一种基于结合异常检测算法的双步故障诊断方法,异常检测模型作为故障检测器,只能用以检测电路是否发生故障,而不能缩小电路的故障源范围;SVM作为故障分类器,在确定电路发生故障的基础上进行故障定位,该方法实际上相当于对电路实时监测的单步故障诊断方法,不适用于大规模电路的故障诊断,而且也没有考虑到故障传播的复杂情况。
在与实例1相同的电路系统环境下,MBPFP与传统BP神经网络、文献[9]、文献[15]中故障定位方法的性能比较,如表5所示。

表5 不同故障定位方法的性能对比 %Tab. 5 Performance comparison of different methods of fault positioning %
与传统BP神经网络和文献[15]中的方法相比,MBPFP的性能明显优于这两种方法;与文献[9]中的方法相比,虽然MBPFP在故障覆盖率上略低于该方法,但其最终的故障定位准确率比文献[9]的方法高9.3个百分点。实验结果表明,MBPFP在大规模数模混合电路的故障诊断中具有较高的故障覆盖率和定位准确率。
3 结语
针对大规模数模混合电路的故障诊断问题,特别是存在故障传播的情况,本文提出了基于故障传播的模块化BP神经网络(MBPFP)故障诊断方法,实现了大规模数模混合电路的故障诊断;特别是针对存在故障传播的情况,通过“分割”故障传播关系实现故障定位,具有较高的故障定位准确率。该方法以元器件的故障模式为研究对象,但同样可以扩展到板级、系统级的故障诊断,适合于系统级的故障诊断;特别是在系统级联结构较为复杂的情况下,该方法可以把复杂的故障情况进行分割,模块化为子系统的故障诊断问题,具有良好的应用前景。
参考文献(References)
[1]谭阳红,何怡刚.模拟电路故障诊断的新故障字典法[J].微电子学,2001,31(4):252-253. (TAN Y H, HE Y G. A new fault dictionary method for fault diagnosis of analog circuits [J]. Microeletronics, 2001, 31(4): 252-253.)
[2]陈文豪,郭子彦,王立,等.复杂机载电子系统故障综合诊断技术研究[J].计算机测量与控制,2016,24(11):1-4. (CHEN W H, GUO Z Y, WANG L, et al. The integrated fault diagnosis technology research based on complex airborne electronic system [J]. Computer Measurement & Control, 2016, 24(11): 1-4.)
[3]DUHAMEL P, RAULT J. Automatic test generation techniques for analog circuits and systems: a review [J]. IEEE Transactions on Circuits and Systems, 1979, 26(7): 411-440.
[4]黄亮.模拟电路故障诊断研究[D].北京:北京交通大学,2012:21-24. (HUANG L. Research on fault diagnosis of analog circuits [D]. Beijing: Beijing Jiaotong University, 2012: 21-24.)
[5]何怡刚,罗先觉,邱关源.模拟电路故障诊断L1估计及其神经网络解法[J].电子科学学刊,1997,15(4):365-371. (HE Y G, LUO X J, QIU G Y. A neural-based nonlinearL1 norm optimization algorithm for diagnosis of networks [J]. Journal of Electronics, 1998, 15(4): 365-371.)
[6]袁海英.基于时频分析和神经网络的模拟电路故障诊断及可测性研究[D].电子科技大学,2006:25-49. (YUAN H Y. Study on fault diagnosis & testability in analog circuits based on time-frequency-domain analysis and neural network [D]. Chengdu: University of Electronic and Technology of China, 2006: 25-49.)
[7]王承.基于神经网络的模拟电路故障诊断方法研究[D].成都:电子科技大学,2005. (WANG C. Research on fault diagnosis in analog circuits based on neural network [D]. Chengdu: University of Electronic and Technology of China.)
[8]AMINIAN F, AMINIAN M, COLLINS H W. Analog fault diagnosis of actual circuits using neural networks [J]. IEEE Transactions on Instrument & Meansurement, 2002, 51(3): 544-550.
[9]谭阳红,何怡刚,陈洪云,等.大规模电路故障诊断神经网络方法[J].电路与系统学报,2001,6(4):25-29. (TAN Y H, HE Y G, CHEN H Y, et al. The method of large scale circuit diagnosis based on neutral network [J]. Journal of Circuits and Systems, 2001, 6(4): 25-29.)
[10]张立永.基于数据挖掘的电路故障分析[D].成都:电子科技大学,2015:41-90. (ZHANG L Y. Fault analysis of circuits based on data mining [D]. Chengdu: University of Electronic and Technology of China, 2015: 41-90.)
[11]曾希雯.基于客观化FMEA方法的故障字典研究与实现[D].成都:电子科技大学,2016:28-64. (ZENG X W. Research and implementation of fault dictionary based on objective FMEA [D]. Chengdu: University of Electronic and Technology of China, 2016: 28-64.)
[12]FUJIWARA H. FAN: a fanout-oriented test pattern generation algorithm [C]// ISCAS 1985: Proceedings of the 1985 IEEE International Symposium on Circuits and Systems. Piscataway, NJ: IEEE, 1985: 671-674.
[13]TAN P N, STEINBACH M, KUMAR V.数据挖掘导论[M].范明,范宏建,译.北京:人民邮电出版社,2014:403-420. (TAN P N, STEINBACH M, KUMAR V. Introduction to Data Mining [M]. FAN M, FAN H J, translated. Beijing: Posts and Telecom Press, 2014: 403-420.)
[14]王健,靳奉祥,史玉峰.模式识别中特征选择与聚类分析[J].测绘工程,2002,11(2):21-24. (WANG J, JIN F X, SHI Y F. Character selection in pattern recognition and cluster analysis [J]. Engineering of Surveying and Mapping, 2002, 11(2): 21-24.)
[15]林超.结合异常检测算法的轴承故障检测研究[D].杭州:浙江大学,2017: 59-78. (LIN C. Research on bearing fault detection based on anomaly detection algorithm [D].Hangzhou: Zhejiang University, 2017: 59-78.)
[16]陈侃,李昌禧.故障传播有向图的故障定位研究[J].自动化仪表,2011,32(4):14-17. (CHEN K, LI C X. Research on the fault localization based on directional graphic of fault propagation [J]. Process Automation Instrumentation, 2011, 32(4): 14-17.)
[17]焦李成.神经网络系统理论[M].西安:西安电子科技大学出版社,1996:52-66. (JIAO L C. Neutral Network System Theory [M]. Xi’an: Xidian University Press, 1996: 52-66.)
[18]DAVIES D L, BOULDIN D W. A cluster separation measure [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1979, 1(2): 224-227.
