基于自主学习行为的教与学优化算法
2018-04-12钟才明
童 楠,符 强,2,钟才明
(1.宁波大学 科学技术学院,浙江 宁波 315212; 2.宁波大学 电路与系统研究所,浙江 宁波 315211)(*通信作者电子邮箱fuqiang@nbu.edu.cn)
0 引言
群体智能方法源于对简单社会系统的模拟,描述了个体通过相互之间的信息交互机制进行合作,通过协作表现出宏观智能行为的群体特征,已成为人工智能领域的新研究热点。与其他方法相比,群体智能方法在鲁棒性、可扩展性、支持分布式并行计算等方面都体现出明显优势,具有很好的应用开发前景。
教与学优化(Teaching-Learning-Based Optimization, TLBO)算法[1]是近年来发展较快的一种新型群体智能方法。TLBO算法利用班级代表所求问题的解空间,班级中的每一名学生则对应解空间中的一个解。所有学生通过教师的课堂教学学习科目知识,同时向身边的同学请教,不断增加自己对科目的知识理解。通过学生群体的迭代学习交流,班级整体知识水平将逐步提高,最终完成对解空间的搜索过程,获取问题的最优解。
TLBO算法结构简单、搜索能力较强,在空气动力设计[2]、车间调度[3]、风力发电[4]、网络规划[5]、电力调节[6]等众多领域中已得到较好的应用与推广。然而,在求解高维复杂非线性问题时,TLBO算法也存在易陷入局部最优区域、发生早熟收敛等问题。为提高算法优化性能,文献[7]通过调节教师人数、采用自适应教学因子、增加讨论学习等手段来激励学生学习兴趣,优化TLBO算法的全局搜索能力;文献[8]提出一种基于精英机制的TLBO算法,保留每次迭代所产生的精英学生,不断加强学生群体的学习能力,强化算法的优化性能;文献[9]通过建立高斯分布模型以实现更多样化的教师选择,并利用随机搜索来平衡局部勘探与全局开发的双重要求,提高了TLBO算法的搜索性能;文献[10]在TLBO算法中引入动态自适应学习因子及动态随机搜索机制,提高了算法的求解精度;文献[11]将Nelder-Mead单纯形算法的局部优化思想融入TLBO算法中,利用扩展、反射、收缩等操作不断修正,提升算法的搜索精度。
本文分析了TLBO算法易于发生早熟现象的机制原因,并从教学过程完整性出发,提出一种基于自主学习行为的TLBO(Self-learning Mechanism-based TLBO, SLTLBO)算法,在教师常规教学以及同伴影响之外,强调学生的自主学习行为与反思对于提高自身科目认知能力的重要作用,并通过标准测试函数对其进行了性能验证。
1 TLBO算法
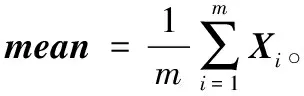
在TLBO算法中,学生主要通过两个阶段获取科目知识,提升自身水平。首先是“教”阶段,学生将在课堂上接受教师的传统授课,进行科目知识学习;其次是“学”阶段,每名学生与身边同学进行相互交流比较,进一步加深对于科目内容的理解。
1.1 “教”阶段
“教”阶段模拟教师的课堂教学过程。在该阶段中,教师对班级内所有学生进行统一授课,时时监测整个班级的接受程度,并对平均水平进行调节,以达到提高全班整体水平的目的。“教”阶段示意图如图1(a)所示。
班级里的任意一名学生Xi在”教”阶段接受教师授课后,所产生的知识更新描述如式(1)所示:
Xi(t+1)=Xi(t)+r1*(Xteacher(t)-TF*mean)
(1)
其中:教学因子TF=round[1+rand(0,1)],取值为1或者2,决定教师对班级内学生群体的教学力度;平均个体mean代表班级平均水平;随机数r1在[0,1]区间取值。
1.2 “学”阶段
“学”阶段模拟学生之间的交流学习。班级内所有学生听取教师传授科目知识以后,每个个体均获得不同程度的知识掌握水平,此时学生根据自身对科目知识的理解,在班级中随机寻找其他学生进行讨论,并对比其他同学与自己的差异,提升自己的知识理解能力。“学”阶段示意图如图1(b)所示。
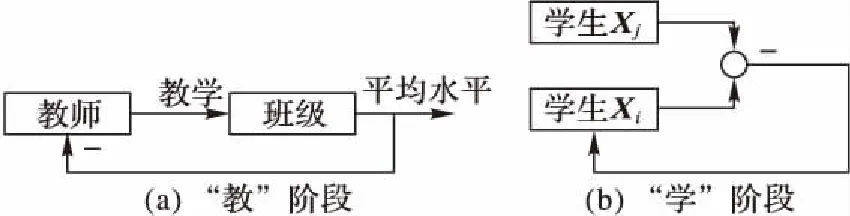
图1 TLBO算法的“教”与“学”阶段示意图Fig. 1 Schematic diagram of TLBO algorithm for "Teaching" and "Learning" stages
学生Xi在“学”阶段中得到的知识更新描述如下所示:
Xi(t+1)=
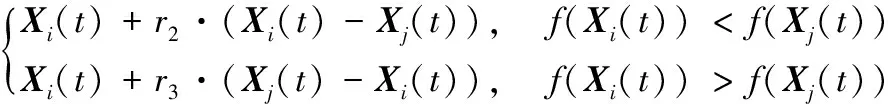
(2)
其中:随机数r2、r3在[0,1]区间取值,f(Xi(t))、f(Xj(t))对应学生Xi、Xj的科目成绩。式(2)表明,如果学生Xj的科目成绩优于学生Xi的科目成绩,则学生Xi向学生Xj执行同向学习;反之,学生Xi执行反向学习。
2 基于自主学习行为的TLBO算法
2.1 TLBO算法机制分析
在TLBO算法中,教师通过”教”阶段带领全体学生实现整体水平提升,不断趋向问题最优解;同时每个学生通过向身边同伴学习,拓展多样化的学习途径,进一步提高自己对知识的掌握层次。与其他同类群体智能方法相比较,TLBO算法具有更多的学习途径,在求解问题时表现出较高的收敛速度及较好的收敛精度。
然而,在实际教学过程中,学生个体的个性化学习对于其能力的提升起着极其重要的作用。班级内的学生群体具有多元智力层次,在相同授课模式下表现出的接受能力不同;同时每名学生作为一个独立个体,学习风格也各不相同。因此,应当允许每个个性化的学生进行差异化学习。然而在TLBO算法中,”教”阶段中的教师依据班级平均零水平组织同一尺度的教学活动,忽视了学生在学习中表现出的差异性,压制了学生个体的学习主动性,因此使得学生群体过早表现出趋同性,抑制了学生群体的再提升能力。虽然学生在“学”阶段可以通过与其他同伴的沟通来获取更多的学习机会,但是,由于其他同伴具备的知识水平也非常有限,制约了有效信息的交互与获取,因此需要在TLBO算法中构建更为完善的教学模式,从而提高算法的搜索性能。
2.2 SLTLBO算法设计
由2.1节分析可知,TLBO算法中的教学环节设置不够完善,其统一教学模式不利于调动所有学生的主观能动性。由于学生个体无法充分发挥自身的学习能力,最终影响整体的学习效果,因此在求解复杂非线性优化问题时,容易过早陷入局部最优区域。鉴于此,本文从教学环节设计出发,对TLBO算法实施了以下优化措施。
2.2.1自主学习阶段
学生Xi在接受课堂教学,并经过同伴交流之后,应当根据自己的学习特点,主动分析自己当前的学习效能,并采取多样化学习行为,真正实现自我提升。首先学生Xi对比自己与教师的差距,向教师要求靠拢,弥补自身不足,进行同向学习;同时考察全班其他同学的学习情况,找出学习最差的学生Xworst,吸取其教训,并参照学生Xworst与自己的差异,进行反向学习,以期获得更好的知识理解。自主学习阶段的数学描述如式(3)所示:
Xi(t+1)=Xi(t)+r4*(Xteacher(t)-Xi(t))-
r5*(Xworst(t)-Xi(t))
(3)
其中,随机数r4、r5在[0,1]区间取值。式(3)表明学生Xi综合考虑最优个体(教师Xteacher)、最差个体(Xworst)与自己的差异性后,分别执行靠近与远离的多样化操作,以获取更好的科目成绩。
2.2.2反思阶段
反思活动是学生吸收外来信息,完成外向学习活动后发起的内在思考,是促进学生开展有效学习的积极探索活动,具有个性化创新的特征,能帮助学生实现自我超越,优化思维品质,有效促进学生对科目知识的认知水平。学生Xi进行反思行为的数学描述如式(4)所示:
Xi(t+1)=normrnd(Xi(t), |Xteacher-Xi(t)|)
(4)
其中:normrnd为满足高斯分布的随机数;Xi(t)、|Xteacher-Xi(t)|分别决定高斯函数的均值与方差。式(4)说明,学生Xi将对自己现有学习状况进行深入思考,并对照教师标准进行反思改进,自发产生变异性调整,有效预防自身停滞在原有水平,完善自己的知识掌握能力。
SLTLBO算法流程如下,算法的时间复杂度为O(m2) 。
BEGIN
初始化,随机设置学生状态,设置学生数m、收敛条件等;
计算每名学生的科目成绩(适应度值);
FORi=1 TOIteration
/*Iteration为迭代次数*/
执行”教”阶段,利用式(1)对学生进行状态更新,如果更新后学生的科目成绩更优,则替换更新前学生;
执行“学”阶段,利用式(2)对学生进行状态更新,如果更新后学生的科目成绩更优,则替换更新前学生;
执行自主学习阶段,利用式(3) 对学生进行状态更新,如果更新后学生的科目成绩更优,则替换更新前学生;
执行反思阶段,利用式(4) 对学生进行状态更新,如果更新后学生的科目成绩更优,则替换更新前学生;
对所有学生个体进行域约束;
结束迭代,输出结果。
END
3 实验与分析
本文选取了10个标准Benchmark测试函数对SLTLBO算法进行性能验证,其中f1~f5为连续性单峰函数,f6~f10为连续性多峰函数,均为具有普遍性、代表不同数据特征的测试函数,常用于检测优化算法的全局搜索能力。其表达式与相关参数如表1所示。
为了更好说明SLTLBO算法的优化性能,本文利用PSO算法[12]、ABC算法[13]以及TLBO算法[8]与SLTLBO算法一起进行测试对比。文中所涉及测试算法均在Windows XP操作系统下,通过Matlab 2013编译调试。硬件环境为Inter Pentium CPU G645(2.9 GHz) 1.82 GB内存。
所有算法的参数设置:种群规模大小为50,最大迭代次数为1 000。测试数据变量维数分别为30、100;另外,PSO算法的惯性权重在[0.2,0.9]区间线性递减,c1=c2=2。
为减少单次算法操作的偏颇性,文中所有算法针对每个测试函数各独立运行20次,统计20次测试结果的均值衡量算法收敛精度,并通过20次结果的方差对比算法鲁棒性。分别在变量维数为30及100的条件下进行了两组测试,结果如表2、3所示。表2显示,在30维的10个函数优化测试中,ABC算法未能得到理论最优值,PSO算法仅在f8函数测试中获得理论最优值,TLBO算法在f8、f10两个测试函数中获取理论最优值,而SLTLBO算法在f1、f3、f7、f8、f9、f10等6个函数中搜索到理论最优值。从整体函数测试结果来看,SLTLBO
算法明显具有更好的收敛精度,搜索能力优于其他对比算法。表3显示,当变量维数增加到100时,PSO算法、ABC算法、TLBO算法的搜索能力明显减弱,如ABC算法在30维f4函数优化过程中表现出较好的搜索性能,但是在100维f4函数的优化结果中却表现最差。而STLBO算法则表现出更加显著的优势,10个测试函数均获得最好的优化结果,并依然在f1、f3、f7、f8、f10等5个函数中搜索到理论最优值,在100维函数的测试结果中也体现出其精准搜索的能力。表2、3的测试结果还显示,SLTLBO算法在维数不同的两组测试中,针对10个函数的20次优化结果方差均很小,这说明SLTLBO算法在处理高维复杂问题时同时也具备较好的鲁棒性。
为了更直观地观察SLTLBO算法的搜索性能,比较SLTLBO算法与其他各算法在搜索效率方面的差异性,绘制f1~f10的适应度进化曲线及统计盒图,限于篇幅限制,只列出变量维数为30时的图形,如图2~11所示。
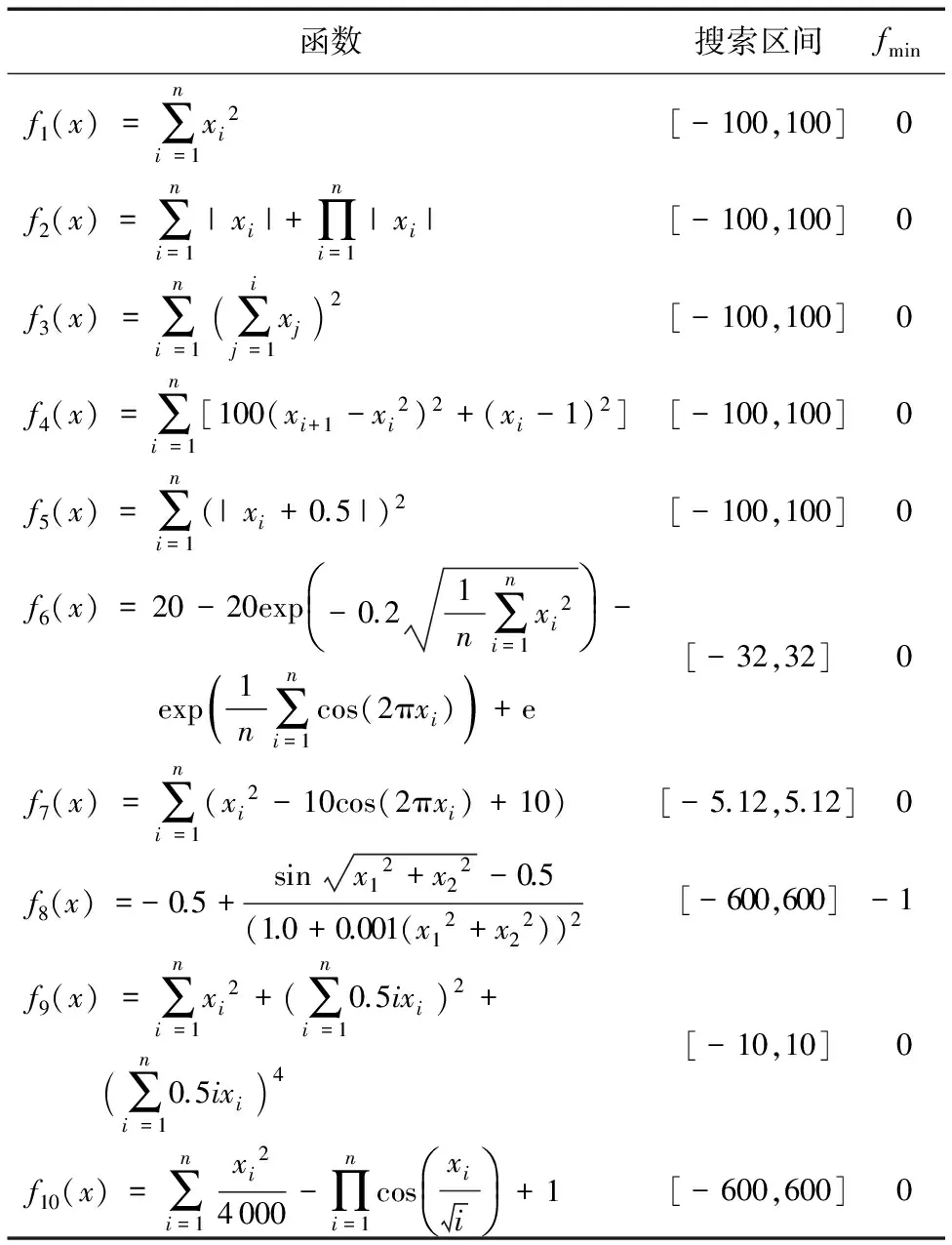
表1 标准测试函数Tab. 1 Standard function used in the experiment
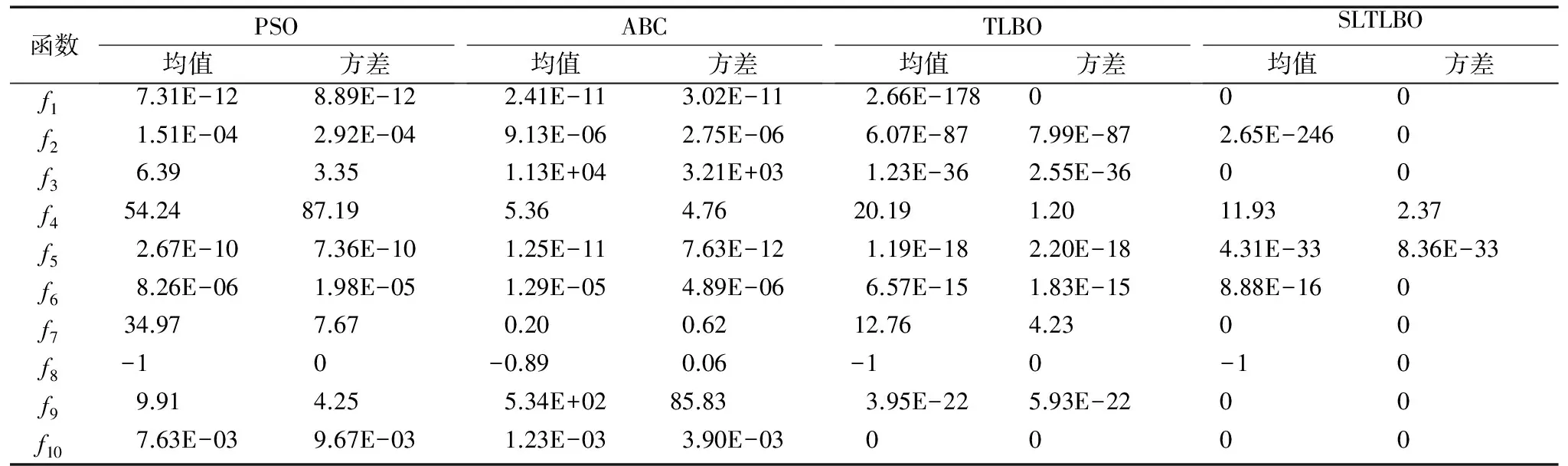
表2 30维函数测试结果对比Tab. 2 Comparison of test results of 30 dimensional functions
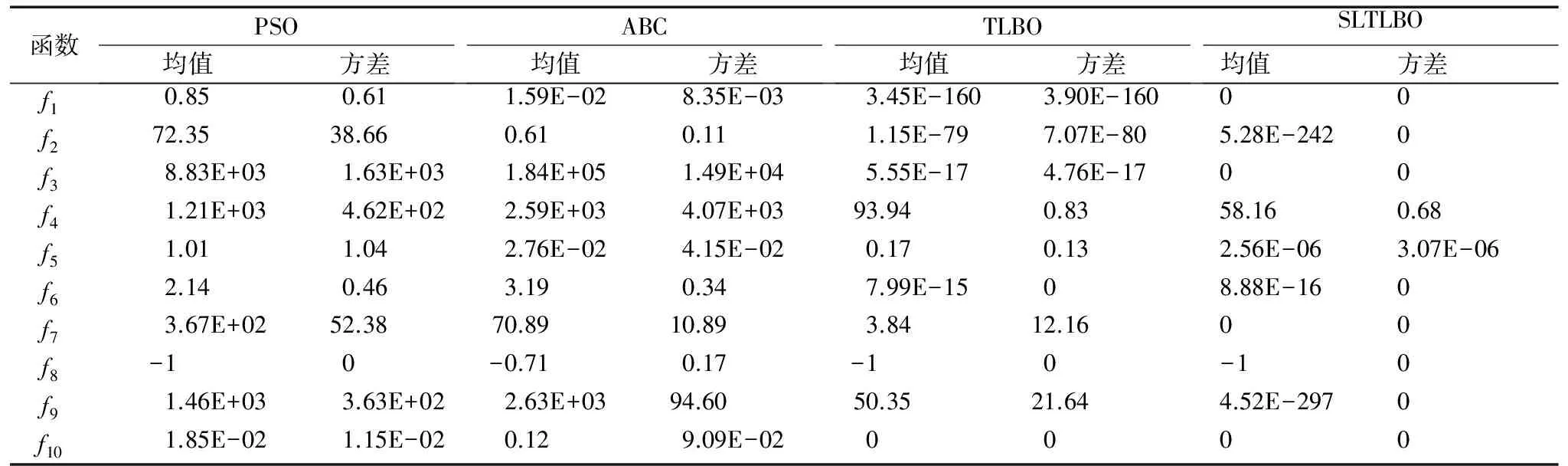
表3 100维函数测试结果对比Tab. 3 Comparison of test results of 100 dimensional functions
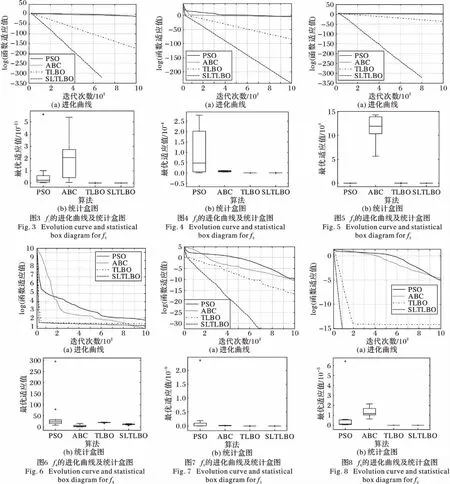
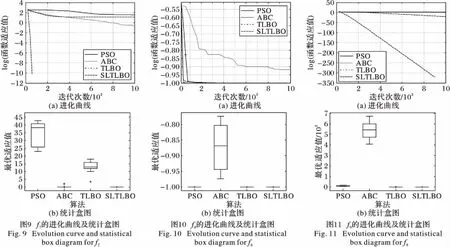
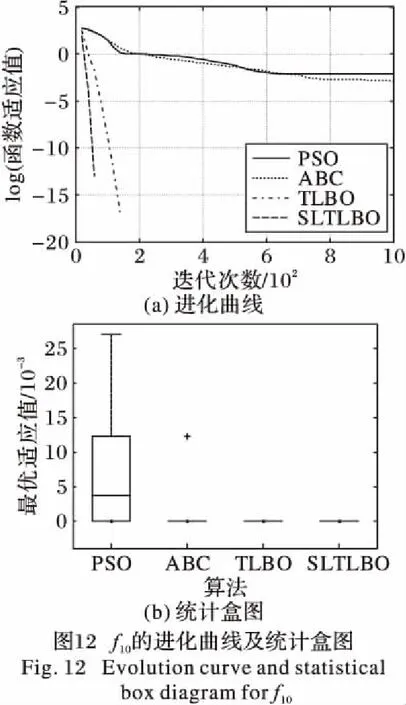
从进化曲线可以看出,SLTLBO算法在200代内即完成了f4、f6、f7、f8、f10等5个函数的目标优化过程,在其他5个函数的进化曲线中也具有最大的曲线斜率,这表明SLTLBO算法在搜索过程中能够迅速判断优化路径,具有较强的搜索效率;而从统计盒图可以看出,不同函数测试条件下,PSO、ABC和TLBO算法在20次优化结果中的不确定性较明显,波动区间较大,而SLTLBO算法在所有函数测试中均具有较小的方差,表现出很好的算法稳定性。
4 结语
本文分析了TLBO算法的优化机制及其易于陷入早熟收敛的原因,从完善教学环节出发,提出了一种基于自主学习行为的TLBO算法(SLTLBO),在传统TLBO算法中的“教”与“学”阶段的基础上,突出学生自主学习的重要性,利用自主学习环节及反思行为增强学生的学习能力,提升其知识水平。利用10个Benchmark测试函数验证了算法搜索能力,并与PSO、ABC和TLBO等算法进行了优化性能对比,实验结果表明,本文提出的SLTLBO算法在收敛精度、收敛速度和鲁棒性等方面均具有明显优势。今后的研究内容主要包括SLTLBO算法的理论分析,以及算法中的结构、参数设置对寻优效果的影响研究。
参考文献:
[1]RAO R V, SAVSANI V J, VAKHARIA D P. Teaching-learning-based optimization: a novel method for constrained mechanical design optimization problems [J]. Computer-Aided Design, 2011, 43(3): 303-315.
[2]QU X, ZHANG R, LIU B, et al. An improved TLBO based memetic algorithm for aerodynamic shape optimization [J]. Engineering Applications of Artificial Intelligence, 2017, 57: 1-15.
[3]朱传军,宋文家,张超勇,等.基于维修时间窗的柔性作业车间调度优化研究[J].中国机械工程,2016,27(10):1337-1343. (ZHU C J, SONG W J, ZHANG C Y, et al. Research on optimization of FJSP based on maintenance time window [J]. China Mechanical Engineering, 2016, 27(10): 1337-1343.)
[4]GÜÇYETMEZ M, ÇAM E. A new hybrid algorithm with genetic-teaching learning optimization (G-TLBO) technique for optimizing of power flow in wind-thermal power systems [J]. Electrical Engineering, 2016, 98(2): 145-157.
[5]SELVAM K, VINOD KUMAR D M, SIRIPURAM R. Distributed generation planning using peer enhanced multi-objective teaching-learning based optimization in distribution networks [J]. Journal of the Institution of Engineers (India): Series B, 2016, 98(2): 203-211.
[6]SAHU R K, PANDA S, ROUT U K, et al. Teaching learning based optimization algorithm for automatic generation control of power system using 2-DOF PID controller [J]. International Journal of Electrical Power & Energy Systems, 2016, 77: 287-301.
[7]RAMA KRISHNA P V, SAO S. An improved TLBO algorithm to solve profit based unit commitment problem under deregulated environment [J]. Procedia Technology, 2016, 25: 652-659.
[8]RAO R V, PATEL V. Comparative performance of an elitist teaching-learning-based optimization algorithm for solving unconstrained optimization problems [J]. International Journal of Industrial Engineering Computations, 2013, 4(1): 29-50.
[9]OUYANG H, WANG Q, KONG X. Modified teaching-learning based optimization for 0-1 knapsack optimization problems [C]// Proceedings of the 29th Chinese Control and Decision Conference. Piscataway, NJ: IEEE, 2017: 973-977.
[10]王培崇.改进的动态自适应学习教与学优化算法[J].计算机应用,2016,36(3):708-712. (WANG P C. Improved dynamic self-adaptive teaching-learning-based optimization algorithm [J]. Journal of Computer Applications, 2016, 36(3): 708-712.)
[11]ZHANG H, LI B, ZHANG J, et al. Parameter estimation of nonlinear chaotic system by improved TLBO strategy [J]. Soft Computing, 2016, 20(12): 4965-4980.
[12]DASHTI S E, RAHMANI A M. Dynamic VMs placement for energy efficiency by PSO in cloud computing [J]. Journal of Experimental & Theoretical Artificial Intelligence, 2016, 28(1/2): 97-112.
