基于密度感知模式的生物序列分类算法
2018-04-12胡耀炜
胡耀炜,段 磊,2,李 岭,韩 超
(1.四川大学 计算机学院,成都 610065; 2.四川大学 华西公共卫生学院,成都 610041;3.四川大学 生命科学学院,成都 610041)(*通信作者电子邮箱leiduan@scu.edu.cn)
0 引言
理解细胞的分子生物机制的一个关键因素是通过对生物序列进行分类来了解不同生物序列的意义和功能[1-2]。随着分子生物学技术的快速发展,产生了大量的生物序列数据,如DNA序列、蛋白质序列等[3]。相比普通的符号序列数据,生物序列数据具有以下明显特点:1)组成生物序列中的符号总数少。例如,一条DNA序列由4种碱基({a,c,g,t})组成,一条蛋白质序列由20种氨基酸组成。在相同长度下,生物序列包含更多的重复出现的符号。2)生物序列的长度较长,例如一条基因或蛋白序列的长度通常在104的级别。3)不同类别的生物序列样本规模不平衡。受限于数据来源和数据采集成本,不同类别的生物序列在样本的长度、数量等统计指标上差别明显。
目前生物序列分类的方法大致可以分为三类:1)利用序列对比工具如FASTA(FAST All)[4]、BLAST(Basic Local Alignment Search Tool)[5]进行序列对比, 找出已知类标的数据库中最为相似的序列;2)基于统计或机器学习的方法,通过一些统计方法抽取序列特征,然后利用机器学习的方法进行序列分类[6-9];3)利用不同的模式挖掘来提取特征并进行分类[10-11]。利用序列对比工具进行分类在数据量较大时需要巨大的计算量;统计或机器学习方法所得到的结果尽管较好但解释性较差;而基于模式的方法具有较强的解释性,但存在分类效果不够理想、运行时间较长的问题。
本文针对基于模式的分类方法,设计了具有可解释性的基于密度感知模式的生物序列分类(Biological Sequence Classifier based on density-aware patterns, BSC)算法,其主要工作包括:1)引入了“密度感知”来评价模式在单条序列中出现的频繁度,并提出了密度感知模型的概念;2)使用“间隔约束”来提高模式匹配的效率;3)在真实的蛋白质序列和基因序列数据上进行翔实的实验,验证了BSC算法有较高的生物序列分类精度和执行效率。
1 问题定义
本文将允许在序列中出现的符号的集合称为符号集,记作Σ。例如,对于DNA序列,Σ={a,c,g,t}。序列由符号集中的元素按序组成,表示为S=e1e2…en(ei∈Σ,1≤i≤n)。用S[i]表示序列S中第i个元素,|S|表示序列S的长度,即S中元素的总数。例如,给定基因序列S=acgcac,S[3]=g, |S|=6。
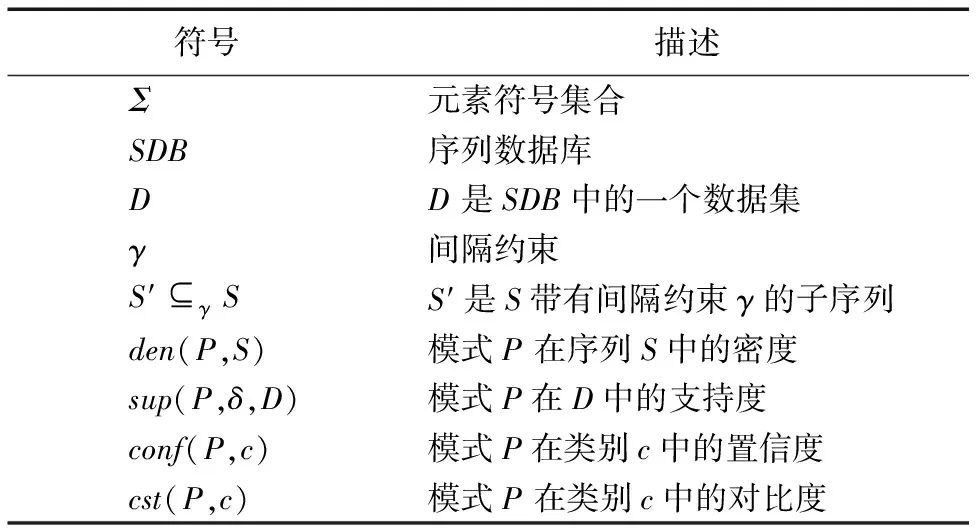
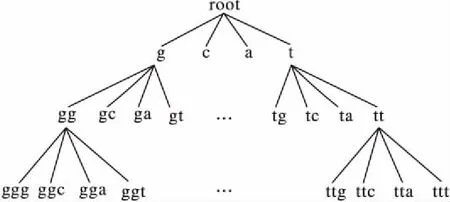
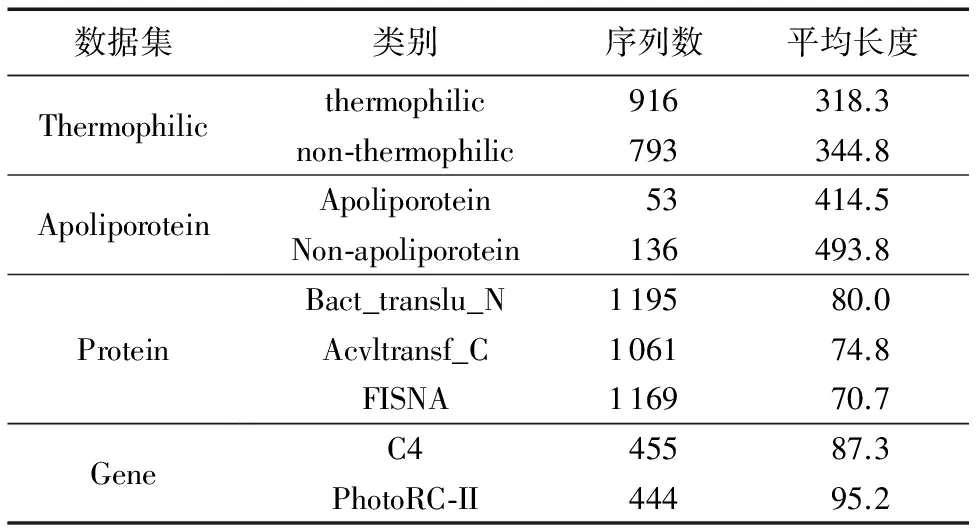
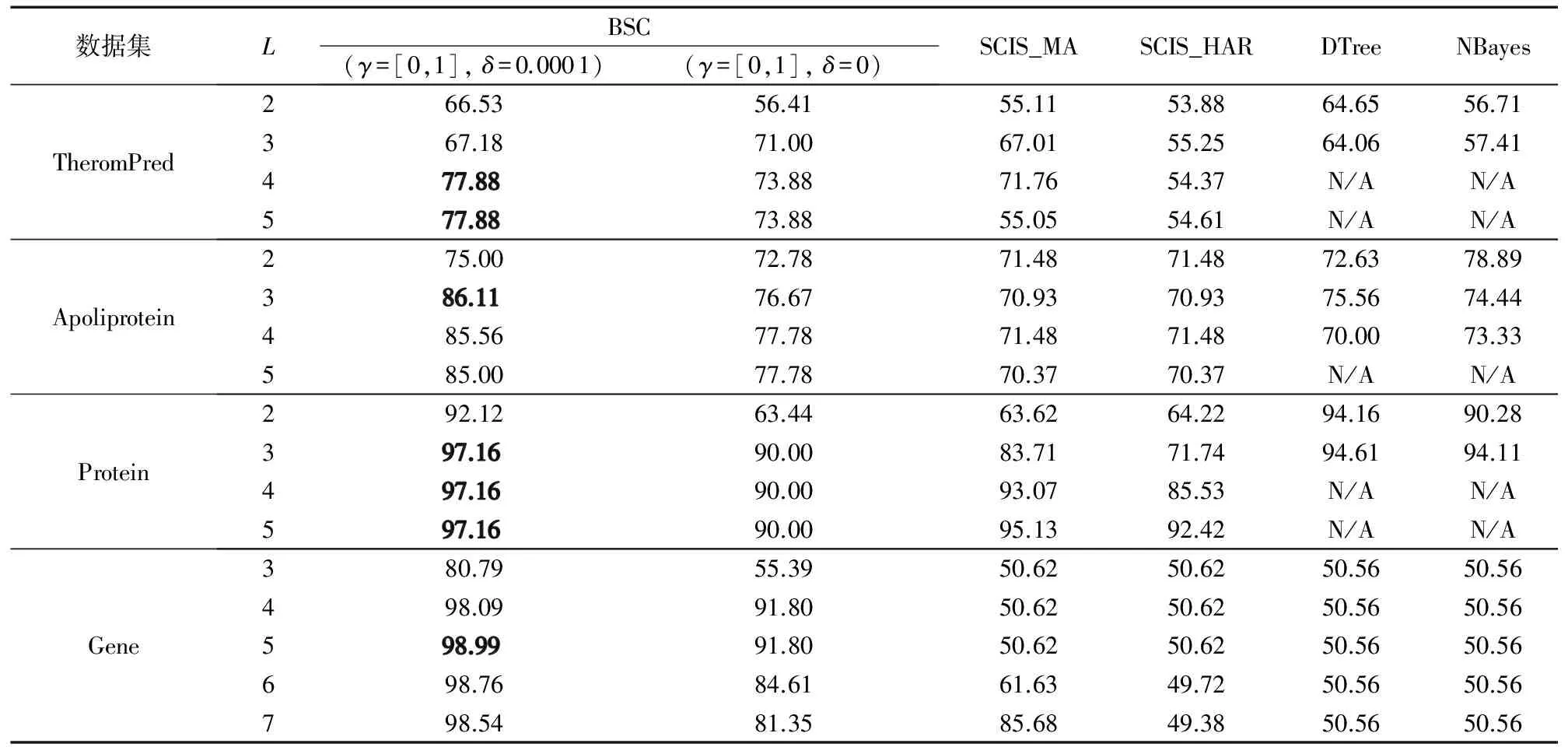
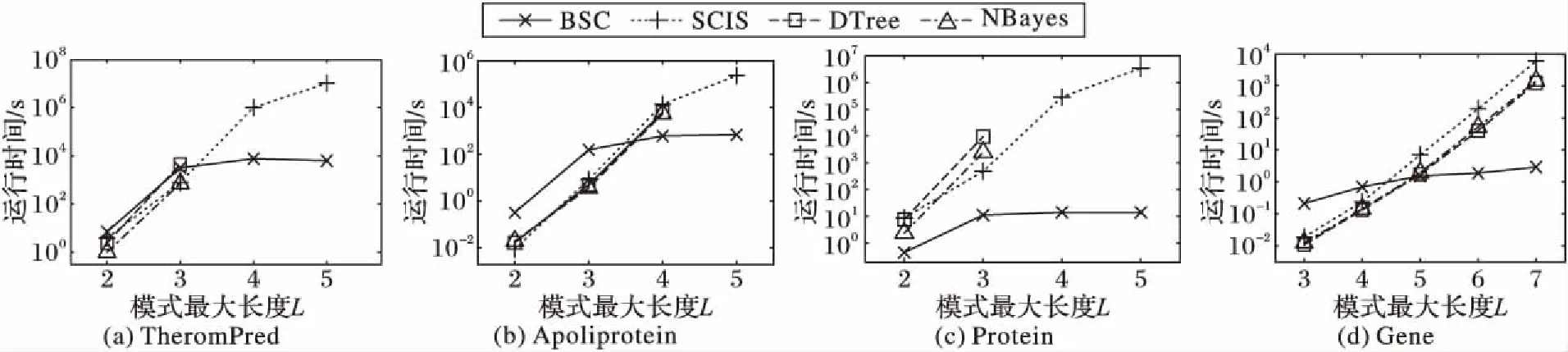
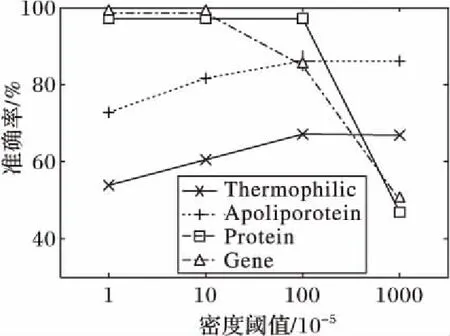
序列S中元素S[i]和S[j](1≤i 给定序列S和序列P,若P=S[k1]S[k2]…S[km],其中1≤k1 若存在实例〈k1,k2,…,km〉∈ins(P,S)满足∀ 1≤i≤m,γ.min≤gap(S,ki,ki+1)≤γ.max,那么称实例〈k1,k2, …,km〉满足间隔约束γ,且P是S的γ-子序列(或称Pγ-匹配S),记作P⊆S。例如:给定序列S=acgcact,序列P=agc,间隔约束γ=[0, 1],则P在S中的实例有〈1,3,4〉。由于gap(S, 1,3)=1∈γ且gap(S,3,4)=0∈γ,因此P⊆S。将ins(P,S)中满足间隔约束γ的实例的集合记为γ-ins(P,S)。容易看出,γ-ins(P,S)⊆ins(P,S)。 给定序列S,间隔约束γ和模式长度l,则序列的长度为l且满足间隔约束γ的实例的数量N为|{〈k1,k2, …,kl〉|∀ 1≤i≤l(1≤ki≤|S|)(∀ 1≤j 定义1密度。给定序列P和S,间隔约束γ,序列P在S的密度den(P,S)为: den(P,S)=|γ-ins(P,S)|/N (1) 若P⊆S,即γ-ins(P,S)≠∅,那么,1/N≤den(P,S)≤1.0。 定义2支持度。给定序列集合D、间隔约束γ和密度阈值δ,序列P的支持度记作sup(P,δ,D),为Pγ-匹配D中序列,且匹配密度不小于δ的序列的个数与D中序列样本总数的比值,即: sup(P,δ,D)=|{S∈D|den(P,S)≥δ}|/|D| (2) 给定支持度阈值,若sup(P,δ,D)≥α,那么称P为密度感知模式。 给定类标签集合C(|C|个类别),序列数据集(Sequential DataBase, SDB)为由一个序列数据对象及其对应的唯一类标签组成的二元组的集合,记作SDB={〈S,c〉},其中S是一条序列,c∈C是S的类标签。为便于描述,将所有类别为c的序列组成的集合记为Dc,即Dc={S|〈S,c〉∈SDB}。那么,给定类标签Ci,Cj∈C,Dci∩Dcj=∅。 定义3置信度。给定序列数据集SDB,间隔约束γ,密度阈值δ。序列P关于类别c的置信度(记作conf(P,c))为: (3) 根据统计学习的思想,某个序列的重要性随着它在该类中出现的次数呈正比增加,同时随着它在其他类中出现的频率呈反比下降。即序列P出现在类别c中频率很高,同时又出现在较少的类中,则P和c类有较大的相关性,可作为用于分类的模式。根据该思想具有以下对比度定义: 定义4对比度。给定序列数据集SDB,间隔约束γ,密度阈值δ,序列P关于类别c的对比度(记作cst(P,c))为: cst(P,c)=sup(P,δ,Dc)×(1+lg(|C|/m)) (4) 其中,m=|{i∈C|sup(P,δ,Di)≥α}|。 表1列出了本文常用的符号及其定义。 表1 符号及定义Tab. 1 Notations and definitions 为了对生物序列数据集分类,本文提出了一种基于密度感知模式的生物序列分类算法BSC。BSC算法主要步骤包括:1)密度感知模式挖掘;2)生成分类规则;3)构建序列分类器。 集合枚举树(图1)是广泛采用的生成频繁模式的算法,BSC算法采用遍历集合枚举树的方式生成候选模式。 图1 DNA集合枚举树Fig. 1 Enumeration tree of DNA set 为了获得较高的执行效率,可根据模式生成算法的性质得到剪枝策略。 引理1给定序列集合D,间隔约束γ,密度阈值δ,支持度阈值α,序列P和P′(P′是P的连续子序列),则sup(P′,δ,D)≥sup(P,δ,D)。 定理1给定序列集合D,间隔约束γ,支持度阈值α,序列P和P′(P′是P的连续子序列),若sup(P′,0,D)<α,则sup(P,δ,D)<α。 证明因为sup(P′,0,D)<α,sup(P′,0,D)≥sup(P,0,D),又因为sup(P,0,D)≥sup(P,δ,D),所以sup(P,δ,D)<α。 证毕。 由定理1可以得到剪枝策略1。 剪枝策略1给定序列集合D,支持度阈值α和序列P,若sup(P,0,D)<α,则剪去集合枚举树中P和P的所有子节点。 本文采用基于广度优先遍历集合枚举树生成候选模式的算法,基本思想为通过拼接两个长度为l的候选模式生成长度为l+1的候选模式[13]。具体地,给定模式P和Q(|P|=|Q|=l), 令pre(P)=P[1]P[2]…P[l-1],suf(Q)=Q[2]Q[3]…Q[l]。 若pre(P)=suf(Q),则可由模式P和Q生成长度为l+1的候选模式P⊕Q=Q[1]P[1]P[2]…P[l]=Q[1]Q[2]…Q[l]P[l]。算法1中给出了BSC算法生成密度感知模式的伪代码。 算法1GENPATTERNS(D,α,δ)。 输入数据集D,支持度阈值α,密度阈值δ; 输出密度感知模式集合F。 Yl←Σ;F←{长度为1的密度感知模式} whileYl≠∅ do Yl+1←∅ Yl←Yl{P∈Yl|sup(P,0,D)<α} forP∈Yl,Q∈Yldo ifpre(P)=suf(Q) then Z=P⊕Q Yl+1←Yl+1∪{Z} ifsup(Z,δ,D)≥αthen F←F∪{Z} endif endif endfor Yl←Yl+1 endwhile returnF 根据算法1可以从数据集SDB的每个类中挖掘到密度感知模式。若在序列集合Dc中挖掘出频繁模式P,则生成的候选分类规则r形如:P⟹c。 数据集中每个类通常会生成大量候选分类规则,若直接应用所有候选规则进行分类不仅会增加计算开销,还将引入低质量的规则导致分类效果不佳。因此,需要对候选分类规则进行评价以便挑选出分类能力强的规则。 置信度反映的是分类规则的确定性。给定分类规则r:P⟹c,置信度阈值β,如果conf(P,c)≥β,则密度感知模式P对c类具有较强分类能力。 对比度反映的是分类规则中密度感知模式P在c类中的重要程度。即c中P出现的频率较高且出现在很少的类时,则P是一个能较好代表c的特征。 文献[14]通过实验验证了当其他条件相同时,模式长度是评价模式分类能力的重要指标。 基于上述分析, 给出以下分类能力评价规则: 给定两个分类规则r1:P⟹c,r2:P′ ⟹c。 1)如果conf(P,c)≥conf(P′,c),那么r1≻r2(r1优于r2)。 2)如果conf(P,c)=conf(P′,c)且cst(P,c)≥cst(P′,c), 那么r1≻r2。 3)如果conf(P,c)=conf(P′,c),cst(P,c)=cst(P′,c)且|P|≥|P′|,那么r1≻r2。 4)如果conf(P,c)=conf(P′,c),cst(P,c)=cst(P′,c),|P|=|P′|且P先于P′生成,那么r1≻r2。 通过评价规则可以对候选分类规则进行排序。按分类能力的高低顺序排好序的分类规则更加利于剪枝并挑选出分类能力较强的规则来构建分类器。 本文候选分类规则剪枝采用数据集覆盖方法[15],即从排好序的候选分类规则集合中依次取规则r对数据集D中的序列进行匹配,若数据集D中至少存在一条序列S满足den(P,S)≥δ,则把此规则加入分类规则集合R中,并把序列S从数据集D中去除。该过程直到数据集D为空或没有满足匹配条件的序列为止。 当数据集SDB的每个类按上述方法进行匹配后,剩余序列最多的类的类标即为默认类标,默认类标在2.3节中用到。 算法2给出了生成分类规则的伪代码。 算法2GENRULES(D,F,δ)。 输入数据集D,密度感知模式集合F,密度阈值δ; 输出分类规则集合R。 R←{P⟹c|P∈F} /*构造分类规则,c为数据集D的类标*/ R←∅ /*初始化分类规则集合R*/ sortR /*按照分类能力评价规则进行排序*/ forr∈Rdo forS∈Ddo ifden(P,S)≥δthen D←DS; endif endfor R←R∪{r} endfor returnR 本节将根据算法2得到的分类规则集合来构建序列分类器,对未知序列进行分类。 在已经取得分类规则集合的情况下,若用分类规则去匹配待分类序列S,则会出现多个分类规则同时匹配S且这些规则属于不同类别的情况,因此需要一种合适的判定方法来判定S属于的类别。 容易想到用投票的方式来进行分类,匹配的规则中某个类的数量最多则预测待分类序列S属于该类。然而,这种方式没有考虑不同分类规则具有不同的可信度,因此分类效果不佳。本文则采用如下方式进行判定: 给定待分类序列S,分类规则集合Rs,则类别c在待分类序列S上的得分为: (5) 若某条分类规则能够匹配到待分类序列,则该规则的置信度作为它的得分累加到该规则预测的类别上。最终,得分最高的类为待分类序列所属的类。算法3给出了构建序列分类器的伪代码。 算法3CLASSIFIER(Rs,S,γ,k)。 输入分类规则集合Rs,待分类序列S,间隔约束γ,k个分类规则; 输出待分类序列S的类标。 对每个类c初始化score(c)为0 count←0 forr∈Rsandcount ifγ-ins(P,S)≠∅ then score(c)←score(c)+conf(P,c) count←count+1 endif endfor ifcount=0 then return 默认类标 returnscore(c)最大的类标 为验证算法的有效性、执行效率和不同参数对算法的影响,在4组真实的蛋白质序列数据集和基因序列数据集上进行实验,包括:Thermophilic数据集[16]、Apoliporotein数据集[17],以及来自于Pfam数据库(http://pfam.xfam.org/)的Protein数据集和Gene数据集。这4组数据特征如表2所示。 为验证BSC算法分类效果,与四种基于模式的可解释性分类算法进行比较。其中:SCIS_HAR、SCIS_MA序列分类算法的代码来自文献[10];另两种算法则采用不同长度的频繁模式作为特征,然后使用解释性较强的决策树和朴素贝叶斯作为分类算法进行分类,且算法由怀卡托智能分析环境(Waikato Environment for Knowledge Analysis, Weka)[18]实现,为便于叙述称这两种算法为DTree和NBayes。 五种算法均采用Java语言编写,代码公开在https://github.com/huyaowei1992/BSC。所有实验都进行了10折交叉验证,即把数据集分成10等份,每次取其中1份作为测试集,其他部分作为训练集,依次进行10次实验,求平均值作为最后结果。实验在配置为Intel Core i7- 4760 3.60 GHz CPU,16 GB内存,Windows 7(64位)操作系统的个人计算机上完成。 表2 实验数据集特征Tab. 2 Characteristics of experimental datasets 为保证实验的一致性,设定所有算法中相同的参数为:支持度阈值α=0.05,置信度阈值β=0.5,使用的分类规则数k=10。因对比的算法需要用户设定生成模式的最大长度L,为了实验的公平,BSC算法也添加该参数进行比较。 表3列出了五种算法在4组数据集中随着模式最大长度L变化的分类精度情况,其中N/A表示算法因为内存溢出而无法完成实验。由表3可以看出, BSC算法在4组数据集上都达到了最好的分类精度,同时L较小时BSC算法已经稳定。SCIS_MA算法和SCIS_HAR算法分类精度随L的增大而提高,但是这两种算法对不同数据集分类效果差别较大。需要注意的是,对比算法在Gene数据的分类精度普遍不高的原因是:Gene数据的字符集比蛋白质更小,只有4个,因此模式的长度较小时,很容易在各类序列中得到匹配,因此需要枚举出比蛋白质更长的模式,分类效果才会有所提升。但是增大模式长度时,需要枚举的模式数量会指数增大,内存需求则会更多,所以根据实验情况,本文列举的模式的最大长度为7。 表3 算法分类准确率比较 %Tab. 3 Comparison of classification accuracy % BSC算法采用基于密度的频繁模式,在长度不同的序列中,密度公式的分子分母都会根据长度的增大而增大,因此会削弱因为序列长度的差别对分类效果产生的影响;且支持度的公式同样采用分数形式,对不同的数据规模有一定的归一化的效果。 实验结果表明,与其他基于模式的分类算法相比,BSC算法对蛋白质数据和基因数据有较高的分类精度,而且在模式长度较小时就可以达到较高精度,算法的有效性因此得到验证。 为验证BSC算法的执行效率,图2记录了有效性实验中算法在4组数据集上随L变化的运行时间。因为SCIS_HAR和SCIS_MA这两个算法挖掘的模式和分类规则都完全一样,只在构造分类器的过程中有所不同,所以运行时间几乎相同。因此,图2中使用SCIS统一表示。由图2可以看出,算法的运行时间随着L增大而变长,但BSC算法运行时间的增长幅度明显小于其他算法。这是因为BSC算法在间隔约束的控制下生成的密度感知模式很少,因此算法的计算开销较小。需要注意的是,BSC算法在L较小时,大部分模式被剪枝策略剪枝,不会再枚举出更长模式,所以运行时间趋于稳定。在图中还可以观察到,其他算法在L较大(L>2)时,运行时间会陡增,这是因为候选模式的规模随L增大呈指数增长。实验结果表明,对生物序列进行分类,BSC算法相对于其他分类算法具有更高的执行效率。 图2 不同模式长度的运行时间Fig.2 Runtime results for different pattern lengths 为了探究不同的参数设置对BSC算法分类精度的影响,本文在4组数据集上进行了关于间隔约束γ和密度阈值δ不同取值时对分类精度影响的实验。设定在蛋白质数据集中L=3,Gene数据集中L=7,其他参数同有效性实验。当某一参数变化时,其他参数保持不变。 图3展示了BSC算法中间隔约束γ变化对分类精度的影响。从3(a)看出,当γ的起始位置变化而间隔大小不变时,对分类精度的影响较小,但整体呈下降的趋势。容易理解,相邻的元素越接近,其间的联系可能越强。如3(b)所示,在γ起始位置不变,间隔变大时,分类精度在蛋白质数据上变化较小,而在Gene数据上变化较大。这是因为在Gene数据集中找到的分类规则比在蛋白质数据集中挖掘的分类规则少。当γ变大时,更多的分类规则将由于不满足密度阈值而被剪枝,最终将大幅影响分类的精度。 图3 不同间隔约束的准确率Fig. 3 Accuracy results for different gap constraints 图4展示了BSC算法中密度阈值δ变化对分类精度的影响。从图4中可见, 当密度阈值设置过大时,两组数据准确率急剧下降,因为密度阈值过大会有大量候选模式被剪枝,最后生成的分类规则过少导致分类精度下降。 通过之前的实验可以看出不同参数对实验结果的影响,本节主要讨论如何对参数进行设置。 对于支持度阈值α和置信度阈值β,本文推荐通常情况下设置α=0.05,这个值相对比较小,能够选出足够的模式;β=0.5是一个比较好的选择,可以选择出全部有分类能力的规则作为后面的备选。 从实验可见,间隔约束γ的初始位置和间隔的设置在数值较小时会有微小的上下波动,但是随着两者数值的增大会呈现下降的趋势;而随着间隔区间的增大,算法的复杂度会不断提升,因此本文推荐间隔约束γ的设置可以在数值较小的范围内使用网格搜索,找到对于不同数据集的最优参数设置。 密度阈值δ的设置同样重要,δ的值太大或者太小都对结果有较大影响。本文推荐可以从δ=0.1开始,每次缩小到原来的1/10进行实验,选择最好的设置。 图4 不同密度阈值的准确率Fig. 4 Accuracy results for different density thresholds 生物序列分类是生命科学领域中的一项重要基础问题。现有的易于解释的基于模式的分类算法对生物序列分类存在分类精度不理想、模型训练时间长的问题。针对这些问题,本文考虑了蛋白质序列和基因序列为代表的生物序列字符集规模小、序列长度较长的特点,设计了基于密度感知模式的生物序列分类算法。在算法中引入了密度的概念,用来挖掘密度较高的频繁模式即密度感知模式,同时采用间隔约束的方式来减少训练分类模型的时间。在4组真实的生物数据集上,将BSC算法与四种序列分类算法进行比较,结果显示BSC算法在分类精度和运行效率上具有更好的表现,同时展示了不同的参数设置对于算法分类准确率的影响并简要分析了原因。 在未来的工作中,将继续改进BSC算法,针对目前的算法需要设置较多参数的问题作出改进。同时,将来可以借鉴目前统计方法,结合模式的易于解释性进行更好改进。除此之外, 将现有算法设计成分布式版本,利用Hadoop、Spark进行大规模数据的序列分类,并将其应用于生物信息领域的数据分析。 致谢感谢周承博士提供的SCIS_HAR和SCIS_MA算法执行程序。 参考文献: [1]LI Y, LU Y, ZHANG F, et al. Protein classification using family profiles [C]// FSKD 2010: Proceeding of the 7th International Conference on Fuzzy Systems and Knowledge Discovery. New York: ACM, 2010: 2212-2216. [2]杨旸.基于机器学习方法的生物序列分类研究[D].上海:上海交通大学,2009:1-2. (YANG Y. Research on biological sequence classification based on machine learning methods [D]. Shanghai: Shanghai Jiao Tong University, 2009: 1-2.) [4]PEARSON W R, LIPMAN D J. Improved tools for biological sequence comparison [J]. Proceedings of the National Academy of Sciences of the United States of America, 1988, 85(8): 2444-2448. [5]ALTSCHUL S F, GISH W, MILLER W, et al. Basic local alignment search tool [J]. Journal of Molecular Biology, 1990, 215(3): 403-410. [6]DAO F-Y, YANG H, SU Z-D, et al. Recent advances in conotoxin classification by using machine learning methods [J]. Molecules, 2017, 22(7): 1057. [7]WEI L, XING P, SHI G, et al. Fast prediction of protein methylation sites using a sequence-based feature selection technique [J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2017, PP(99): 1. [8]LIU B, XU J, FAN S, et al. PseDNA-Pro:DNA-binding protein identification by combining Chou’s PseAAC and physicochemical distance transformation [J]. Molecular Informatics, 2015, 34(1): 8-17. [9]熊贇,陈越,朱扬勇.ProFaM:一个蛋白质序列家族挖掘算法[J].计算研究与发展,2007,44(7):1160-1168. (XIONG Y, CHEN Y, ZHU Y Y. ProFaM: an efficient algorithm for protein sequence family mining [J]. Journal of Computer Research and Development, 2007, 44(7): 1160-1168.) [10]ZHOU C, CULE B, GOETHALS B. Pattern based sequence classification [J]. IEEE Transactions on Knowledge and Data Engineer, 2016, 28(5): 1285-1298. [11]MULDER N J, KERSEY P, PRUESS M, et al. In silico characterization of proteins: UniProt, InterPro and Integr8 [J]. Molecular Biotechnology, 2008, 38(2): 165-177. [12]ZHANG M, KAO B, CHEUNG D W, et al. Mining periodic: patterns with gap requirement from sequences [C]// SIGMOD ’05: Proceeding of the 2005 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2005: 623-633. [13]WANG X, DUANG L, DDONG G, et al. Efficient mining of density-aware distinguishing sequential patterns with gap constraints [C]// DASFAA 2014: Proceeding of the 2014 International Conference on Database Systems for Advanced Applications, LNCS 8421. Cham: Springer, 2014: 372-387. [14]TSENG V S, LEE C-H. Effective temporal data classification by integrating sequential pattern mining and probabilistic induction [J]. Expert Systems with Applications, 2009, 36(5): 9524-9532. [15]LIU B, HSU W, MA Y. Integrating classification and association rule mining [C]// KDD’98: Proceeding of the 4th International Conference on Knowledge Discovery and Data Mining. Menlo Park, CA: AAAI Press, 1998: 80-86. [16]LIN H, CHEN W. Prediction of thermophilic proteins using feature selection technique [J]. Journal of Microbiological Methods, 2010, 84(1): 67-70. [17]TANG H, ZOU P, ZHANG C M, et al. Identification of using feature selection technique [J]. Scientific Reports 6, 2016: 30441. [18]HALL M, FRANK E, HOLMES G, et al. The WEKA data mining software: an update [J]. ACM SIGKDD Explorations, 2009, 11(1): 10-18.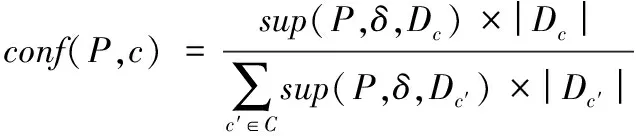
2 BSC算法设计
2.1 密度感知模式挖掘
2.2 生成规则
2.3 构建序列分类器
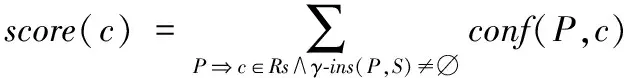
3 实验与分析
3.1 实验数据及环境
3.2 有效性实验
3.3 执行效率验证
3.4 不同参数对算法的影响

3.5 参数设置讨论
4 结语
