熵权贝叶斯模型在珊溪水库水环境质量评价的应用
2018-04-12万哲慧冯孙林贾晓琼施胜亮
万哲慧,王 珅,冯孙林,贾晓琼,施胜亮
(浙江省温州市环境监测中心站,浙江 温州 325000)
在浙江省“五水共治”与“全面剿灭劣Ⅴ类”的新时代背景下,“保供水”作为“五水共治”的重要一方面,温州市各级人民政府及其环境保护部门非常重视饮用水地的环境保护工作。《地表水环境质量标准(GB3838-2002)》作为评判水质的依据是衡量各级人民政府环保工作成效的唯一标尺。水环境质量评价工作亦是环境监测部门十分重要的工作之一。区域流域水质的不确定性导致水质评价工作难度较大。常见的评价方法如单因子法、综合评价法等由于各自局限性,不能客观地反映水环境质量的实际状况。
基于概率与数理统计的贝叶斯理论建立各类水质评价因子不确定性概率矩阵[1],计算赋权之后的后验概率和的数值来确定属于各类水质概率能有效解决水质评价遇到的困难。近年来国内外学者将贝叶斯理论应用于环境保护领域中的地表水、地下水资源决策管理、大气健康风险评价与水质污染事故风险评估取得了良好的效果[2-7]。因此,将模糊数学概率论法贝叶斯理论水质评价方法应用于饮用水源地二级保护区,并与其他评价方法相比较,以期寻找适宜的评价方法为属地环境保护部门决策提供科学依据。
1 珊溪水库概况与水样采集
珊溪水利枢纽(东经119°50′~120°20′,北纬47°39′~47°48′),主要由珊溪水库和赵山渡引水工程(即赵山渡水库)两部分组成,为温州地区主要水源之一。珊溪水库正常蓄水位142 m,总库容18.42 亿m3,为多年调节水库。
珊溪水库位20个采样点位如图1所示。温州市环境保护局珊溪水利枢纽分局依据《水质 湖泊和水库采样技术指导(GBT 14581-1993)》、《水质 采样方案设计技术术规定(HJ 495-2009)》承担珊溪水库库区和交接断面水质公开方案的布点与采样作业。依据《地表水环境质量标准(GB3838-2002)》附录中推荐监测方法,经实验室分析获得相关指标的监测数据。
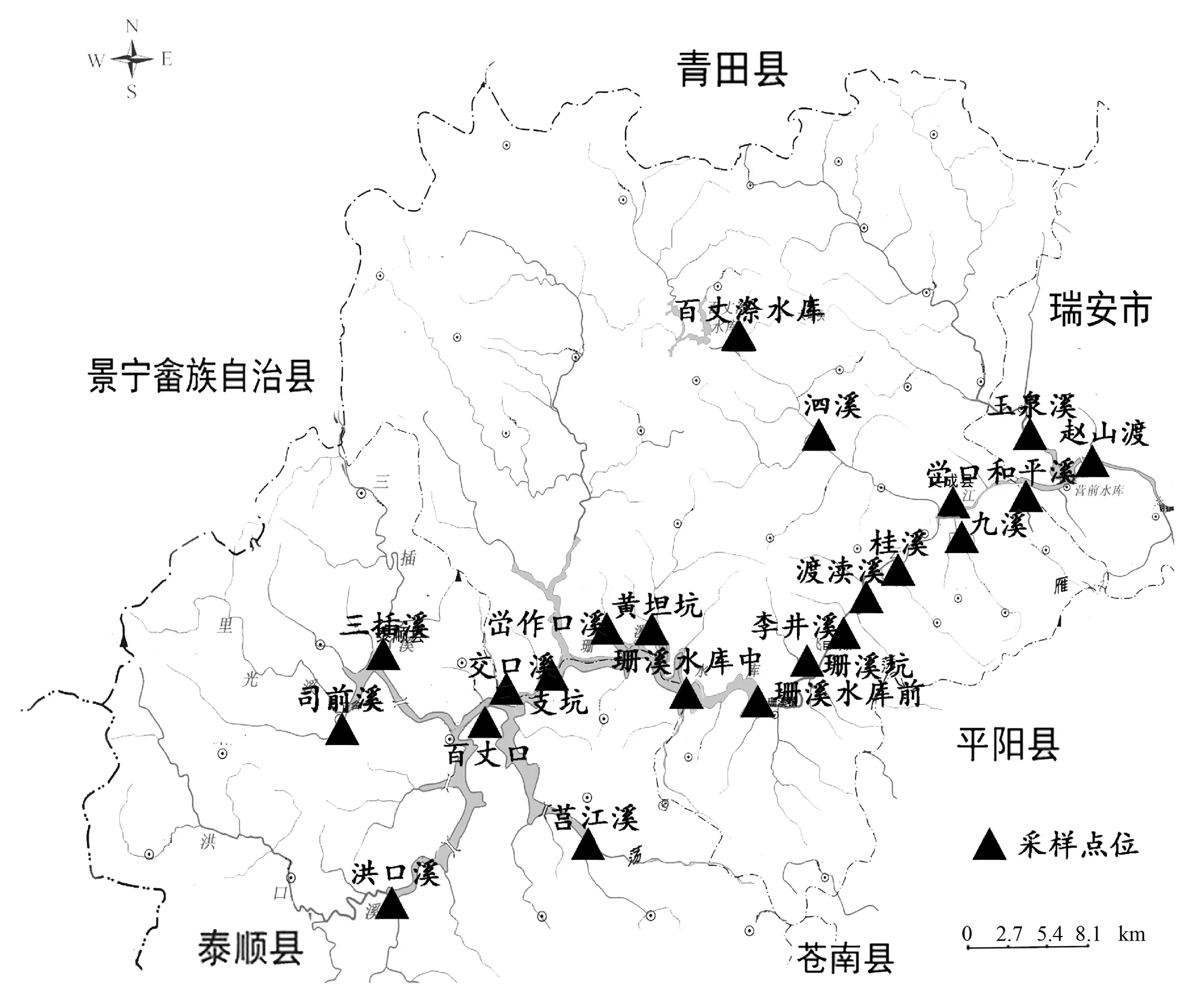
图1 珊溪水库水质采样布点示意图Fig.1 Distribution of sampling sites in Shanxi reservoir
2 基于熵权的贝叶斯评价方法
2.1 水质评价中的贝叶斯法
概率论与数理统计贝叶斯(Bayes)公式在水环境质量评价中可做如下定义:假设样本空间为Q,Bi(i=1,2,3,…,n)是该空间的有限划分并且P(Bi)>0;对任意A为Q的真子集,P(A)>0,则:
(1)
式中:P(Bi|A),P(A|Bi)皆为条件概率。
运用式(1)对某流域监测站位进行水环境质量评价时,式(1)可理解为Bi表示水质类型,即《地表水环境质量标准(GB3838-2002)》表1中规定的Ⅰ~Ⅴ类各标准限值。A表示某监测站位某监测项目实测数据,所选某监测项目与Bi标准限值相对应。P(Bi)为先验概率,在无监测数据的情况下,某监测站位属于某水质级别的概率是相同的[8,9]。因此,该监测站位先验概率表示式(2):
(2)
P(A|Bi)为似然概率,表征监测站位水质指标数值大小。水质较优的情况下,出现较劣指标的概率较小;反之,水质较劣情况下,出现较劣的概率较大。
P(Bi|A)为后验概率,表征在已获得某监测站位水质监测项目的条件下,断面水质属于某水质级别的概率。
似然概率P(A|Bi)采用几何概率中的距离计算法式(3),以某监测站位某水质监测项目与水质项目标准之间的距离D绝对值的倒数运算。
(3)
D=|x-y|
式中:x为某监测站位某水质监测项目实测值;y为该实测值对应标准值;D值越大表征该监测项目属于该水质等级的概率越小。
诸多监测项目条件下的综合水质后验概率用Pi表示,计算方法为式(4)。
(4)
(5)
式中:wj表示j监测项目的权重;Pi即为n个监测项目赋权的后验概率和。依据最大概率原则确定某监测站位水质级别即式(5)。
2.2 熵权法权重赋值
确定水质评价因子在评价体系中权重的方法报道很多,主要分为主观、客观、主观客观相结合方法计算权重[10]。各种方法各有优势,如主观评价法中的专家评分,比较法简便容易操作;客观法不依赖人为判断,如主成分分析法,因子分析法等;主客观结合法将上述两者结合起来,如主成分分析法与多元统计法结合,相对较复杂。在同一水体环境各不同监测站位获得的各监测项目数据采用熵权法,构造评价项目测定值与监测站位矩阵。评价项目之间权重分配取决于评价项目样本信息量的大小与评价项目内的数据差异性。
熵源于物理化学的重要概念,其表征系统混乱程度,通常用G来表示;而熵权是由C.E.Shannon将熵的概念引入信息论发展起来的。熵权法已广泛应用于社会经济,工程技术等各个领域[11]。在水环境质量评价方面应用熵权法研究样本各参数的权重赋值时主要关注以下几个步骤。
2.2.1矩阵的建立与标准化
将原始数据整理为原始矩阵A并标准化。
A=(Rij)m×n
(6)
根据《地表水环境质量标准(GB3838-2002)》表一中除水温、pH值、溶解氧外,其他项目皆为浓度低者为优。式(7)中Rij表示第j个监测站位在第i项监测项目的标准限值。
(7)
2.2.2计算熵值
第i项监测项目的熵值用Gi表示,其计算公式如(8)。
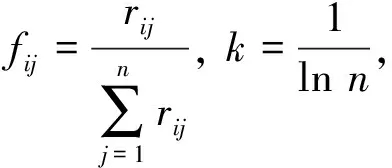
(8)
2.2.3计算熵权权重
计算第i项监测项目的熵权赋值计算公式如(9)所示,显然Wi取值范围在0~1闭区间,同时所有监测项目Wi代数和为1。
(9)
河流湖库水质评价因子主要分感官因子、氧平衡因子、营养盐因子、毒物因子、微生物因子等。考虑到珊溪水库饮用水水源地一级保护区较关注富营养化程度,因此选用氧平衡因子中的高锰酸盐指数、营养盐因子中的营养元素N、P和毒物因子氨氮。上述评价因子的标准限值如表1所示。
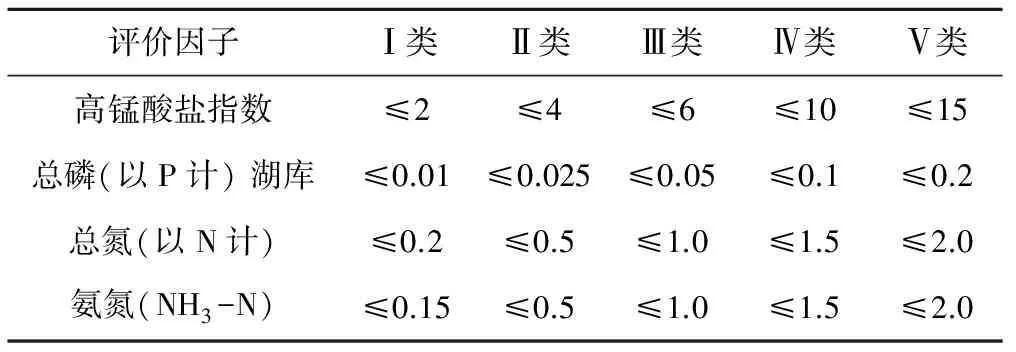
表1 GB3838-2002基本项目标准限值节选 mg/L
3 结果讨论
取2014年珊溪水库及其入库支流各监测站位水质评价项目每月例行监测数据,计算其年浓度平均值,选择高锰酸盐指数、氨氮、总磷、总氮与《地表水环境质量标准(GB3838-2002)》中对应评价项目合成为多目标决策矩阵Xm×n(m=25、n=4),如表2所示。经计算20个监测站位熵权权重为高锰酸盐指数WCOD=0.268,氨氮WNH3-N=0.238,总磷WTP=0.248,总氮WTN=0.245;从计算结果可以看出高锰酸盐指数权重较其他三者高,因此高锰酸盐指数对珊溪水库水质评价有相对较大影响。

表2 监测站位多目标决策矩阵 mg/L
由式(1)贝叶斯公式在水环境质量评价中可进行如下解释:后验概率=先验概率×调整因子。其中,后验概率即Pi,先验概率取值相同,似然概率可视为调整因子[12]。预先估计了“先验概率”,在后续的实验中获得各监测项目的实测值来判断实验是增强还是削弱了“先验概率”,因此得到更接近实际水质状况的“后验概率”。调整因子值>1,“先验概率”被增强,表示水质属于某水质类别的可能性变大。调整因子值=1,其他事件无助于判断水质所属类别的可能性。调整因子<1,表示“先验概率”被削弱,水质属于某水质类别的可能性变小。
各监测站位经熵权加权计算的贝叶斯矩阵X*如表3所示。从表3可以看出,除黄坦坑为Ⅲ类水质的概率为0.295,平和溪、峃作口溪分别有0.454、0.417概率为Ⅱ类水质,其他各监测站位均属于I类水体,其中泗溪概率最高0.681,李井坑概率最低0.338。监测站位两种水质评价方法比较结果如表4所示。

表3 监测站位熵权加权贝叶斯矩阵Fig.3 entropy-weighted Bayes matrix of sampling sites
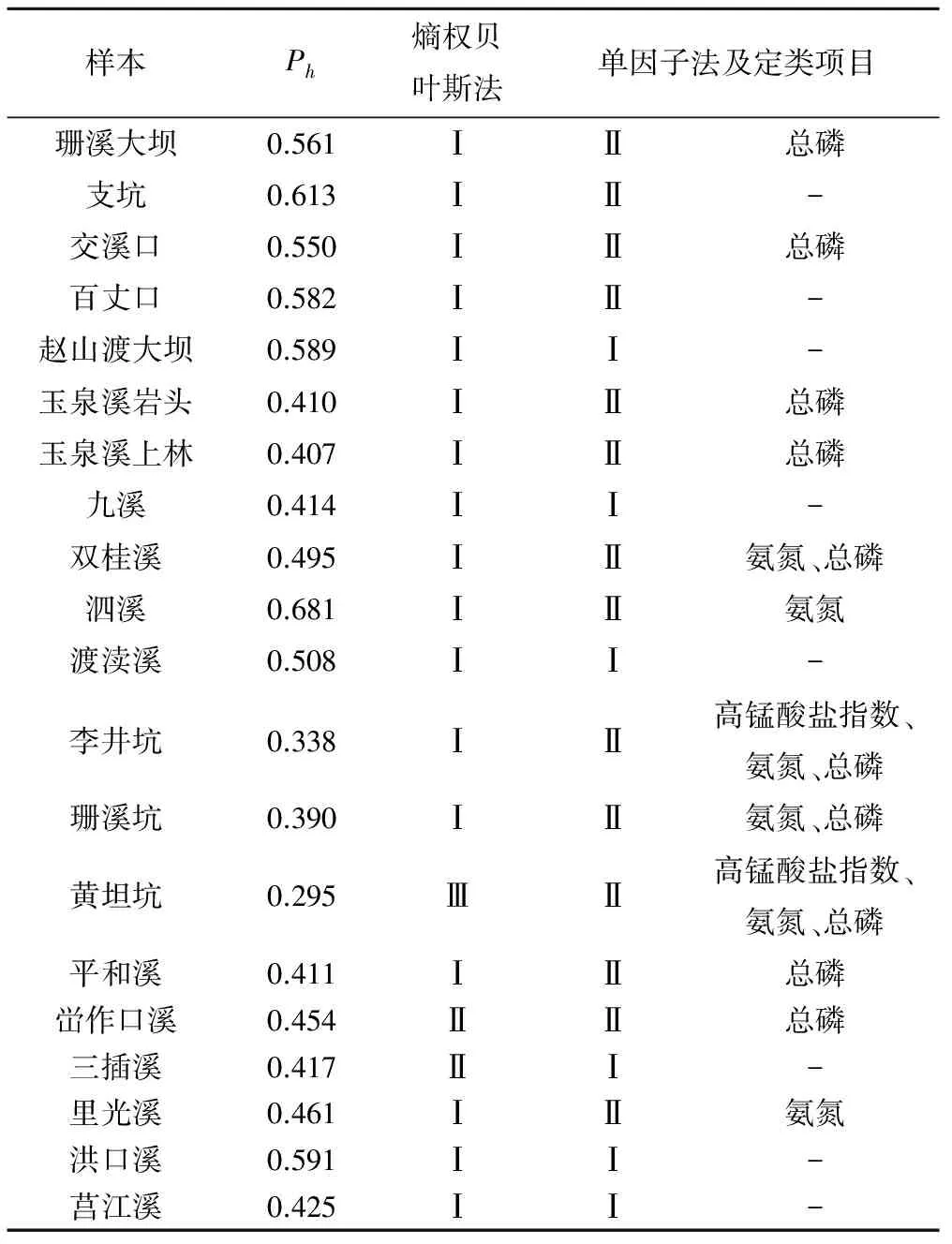
表4 监测站位加权贝叶斯后验概率水质等级与单因子水质评价方法比较Tab.3 Comparison entropy weight Bayes posterior probability of water quality grade and other water quality assessment methods
根据环境保护部《地表水水环境质量评价办法(试行)(环办[2011]22号)》单子因子法评价水质排除了总氮指标,评价结果相对贝叶斯评价结果趋保守,仅6个监测站位评价为I类水质,其他监测站位均为II类水体。因此,两种水质评价方法比较,熵权贝叶斯法更贴近实际。
4 贝叶斯法评价水环境质量的适用范围与解决对策
应用贝叶斯法评价水环境质量时,选用《地表水环境质量标准(GB3838-2002)》中表一分级标准限值不同项目如溶解氧、高锰酸盐指数、氨氮、总磷、总氮、硫化物等。pH值、氟化物、氰化物、挥发酚、各种金属元素等等监测项目,由于各级标准间取值相同导致贝叶斯计算结果出现偏差,难以判断监测站位水质等级概率。因此,建议国家有关部门组织相关领域专家继续细化《地表水环境质量标准》(GB3838-2002)中的相关监测项目各等级取值。
贝叶斯法公式(3)中D=|x-y|, 当实测值与标准值一致时,D值为零,则D的倒数不存在,无法计算似然概率P(A|Bi)。因此,需要调整实测值的有效位数,避免与标准值一致导致矩阵计算无法进行。
5 结 语
利用基于熵权贝叶斯法评价了珊溪水库及入库支流水体20个监测站位的水环境质量。评价结果显示20个监测站位水质在Ⅲ类以上,珊溪大坝及赵山渡大坝饮用水源取水口等17个监测站位达到I类水体标准,水质较优,黄坦坑水质相对较差。与单因子法相比,熵权贝叶斯法评价模型客观反映了监测站位水质的实际状况。运用模糊数学与概率论评价水环境质量更有利于珊溪水库水库水源地保护区水利枢纽的分类管理。
参考文献:
[1]徐悦,周林飞,成遣.基于两种方法的石佛寺人工湿地水质综合评价与分析[J].节水灌溉, 2017,(4):106-109,117.
[2]Molina J L, Bromley J, Garcia-Arostegui J L, et al. Integrated Water Resources Management of Overexploited Hydrogeological Systems Using Object-oriented Bayesian Networks[J].Enviromental Modelling & Software, 2010,25(4):383-397.
[3]Blangiardo M, Richardson S, Gulliver J, et al. A Bayesian Analysis of the Impact of Air Pollution Episodes on Cardio-respiratory Hospital Admissions in the Greater London Area[J]. Statistical Methods in Medical Research,2011,20(1):69-80.
[4]卢文喜,罗建男,龚磊,等.基于贝叶斯网络的地下水环境系统决策管理研究[J].地学前缘,2010,17(6):247-254.
[5]江善虎,任立良,刘淑雅,等. 基于贝叶斯模型平均的水文模型不确定性及集合模拟[J]. 中国农村水利水电,2017,(1):107-112,117.
[6]杜拉,纪昌明,李荣波,等. 基于小波-BP神经网络的贝叶斯概率组合预测模型及其应用[J]. 中国农村水利水电,2015,(7):50-53.
[7]孙鹏程,陈吉宁.基于贝叶斯网络的河流突发性水质污染事故风险评估[J].环境科学,2009,30(1):47-51.
[8]毛志,陈亚丽.基于贝叶斯公式的河流水质综合评价-以铜仁市锦江河为例[J].铜仁学院学报,2016,18(4):150-153.
[9]卞建民,王瑞,李潇瀚. 基于贝叶斯的伊通河水质综合评价[J]. 节水灌溉,2011,(5):31-33,40.
[10]卫晓婧,刘攀.不确定性水文预报在三峡水库的应用研究[J]. 节水灌溉,2013,(12):37-39.
[11]杜娟娟.基于不同赋权方法的模糊综合水质评价研究[J].人民黄河,2015,37(12):69-73.
[12]候佑泽,秦天玲,严登华,等. 基于贝叶斯理论的武烈河水质综合评价[J].南水北调与水利科技,2012,10(1):94-97,101.
