概率综合演练A卷

一、选择题

1.已知事件A,B,且则A,B之间的关系一定是( )。

A.两个任意事件

B.互斥事件

C.非互斥事件

D.对立事件

2.从装有2个红球和2个黑球的口袋内任取2个球,那么互斥而不对立的两个事件是( )。

A.“至少有1个黑球”与“都是黑球”

B.“至少有1个黑球”与“都是红球”

C.“至少有1个黑球”与“至少有1个红球”

D.“恰有1个黑球”与“恰有2个黑球”

4.某产品分甲、乙、丙三级,其中乙、丙两级均属次品,在正常生产情况下,出现乙级品和丙级品的概率分别是5%和3%,则抽检一件产品是正品(甲级)的概率为( )。

A.0.95 B.0.97

C.0.92 D.0.08

5.容量为20的样本数据,分组后的频数如表1所示,则样本数据落在区间[10,40)上的概率为( )。

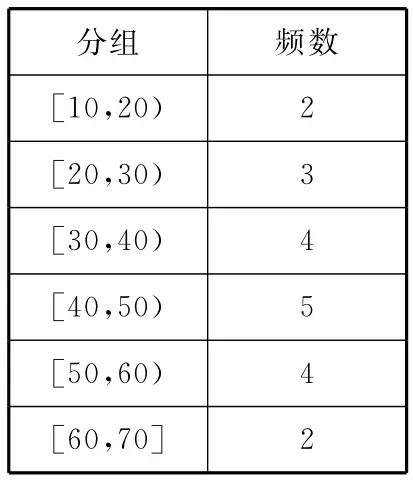
表1

A.0.35 B.0.45

C.0.55 D.0.65

6.我国古代数学名著《数书九章》有“米谷粒分”题：粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )。

A.134石 B.169石

C.338石 D.1365石

7.从某校高二年级的所有学生中,随机抽取20人,测得他们的身高(单位：cm)分别为：162,153,148,154,165,168,172,171, 173,150,151,152,160,165,164,179,149, 158,159,175。

根据样本频率分布估计总体分布的原理,在该校高二年级的所有学生中任抽1人,估计该生的身高在155.5～170.5cm之间的概率约为( )。

8.若随机事件A,B互斥,事件A,B发生的概率均不等于0,且P(A)=2-a,P(B)=4a-5,则实数a的取值范围是( )。

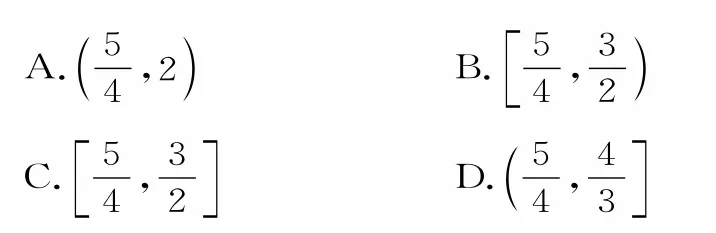
9.掷一个骸子的试验,事件A表示“出现小于5的偶数点”,事件B表示“出现小于5的点”,则在一次试验中,事件发生的概率为( )。

10.如图1所示,A是圆O上一定点,在圆O上其他位置任取一点A',连接A A',得到一条弦,则此弦的长度小于或等于半径长度的概率为( )。

图1

11.在区间[0,1]上随机取一个数x,则事件“l o g0.5(4x-3)≥0”发生的概率为( )。

12.一个质地均匀的正四面体玩具的四个面上分别标有1,2,3,4这四个数字,若连续两次抛掷这个玩具,则两次向下的面上的数字之积为偶数的概率是( )。

13.从集合A={-3,-2,-1,2}中随机选取一个数记为k,从集合B={-2,1,2}中随机选取一个数记为b,则直线y=k x+b不经过第四象限的概率为( )。

14.已知集合A={1,2},B={1,2,3},分别从集合A和B中随机取一个数a和b,确定平面上的一个点P(a,b),记“点P(a,b)落在直线x+y=n上”为事件Cn(2≤n≤5, n∈N),若事件Cn发生的概率最大,则n的所有可能值为( )。

A.3 B.4

C.2和5 D.3和4

15.某公司有一批专业技术人员,其中年龄在35～50岁的本科生和研究生分别有30人和20人,现用分层抽样法在35～50岁年龄段的专业技术人员中抽取一个容量为5的样本,将该样本看成一个总体,从中任意抽取3人,则至少有1人为研究生的概率为( )。

16.从一箱产品中随机抽取1件,设事件A={抽到一等品},事件B={抽到二等品},事件C={抽到三等品},且已知P(A)=0.65,P(B)=0.2,P(C)=0.1,则事件“抽到的不是一等品”的概率为( )。

A.0.7 B.0.65

C.0.35 D.0.3

17.在5张电话卡中,有3张移动卡和2张联通卡,从中任取2张,若事件“2张全是移动卡”的概率是的事件是( )。

A.至多有1张移动卡

B.恰有1张移动卡

C.都不是移动卡

D.至少有1张移动卡

18.图2所示的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字,那么概率为被污损,则甲的平均成绩超过乙的平均成绩的概率是( )。

图2

19.如图3,大正方形的面积是34,四个全等直角三角形围成一个小正方形,直角三角形的较短边长为3,向大正方形内抛撒一枚幸运小花朵,则小花朵落在小正方形内的概率为( )。

图3

20.有一个底面圆的半径为1、高为2的圆柱,点O为这个圆柱底面圆的圆心,在这个圆柱内随机取一点P,则点P到点O的距离大于1的概率为( )。的概率,p2为事件

21.在区间[0,1]上随机取两个数x,y,记p1为事件的概率,则( )。

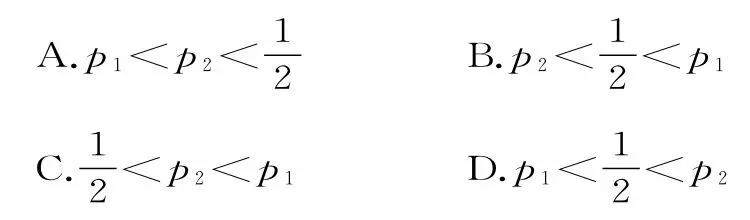
22.在区间[-π,π]内随机抽取两个数分别记为a,b,则函数f(x)=x2+2a x-b2+ π2有零点的概率为( )。

二、填空题

23.给出下列三个命题：

①有一大批产品,已知次品率为10%,从中任取100件,必有10件是次品;

②做7次抛硬币的试验,结果3次出现正面,因此正面出现的概率是

③随随机事件发生的频率就是这个随机事件发生的概率。

其中错误命题的个数为____。

24.某城市2016年的空气质量状况如表2所示。

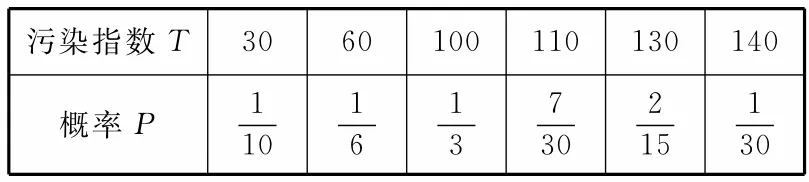
表2

其中污染指数T≤50时,空气质量为优;50＜T≤100时,空气质量为良;100＜T≤150时,空气质量为轻微污染。该城市2016年空气质量达到良或优的概率为____。

25.从2名男生和2名女生中任意选择2人在星期六、星期日参加某公益活动,每天1人,则星期六安排1名男生、星期日安排1名女生的概率为____。

26.口袋内装有一些除颜色不同之外其他均相同的红球、白球和黑球,从中摸出1个球,摸出红球的概率是0.42,摸出白球的概率是0.28,若红球有21个,则黑球的个数为____。

27.已知某台纺纱机在1h内发生0次,1次,2次断头的概率分别是0.8,0.12,0.05,则这台纺纱机在1h内断头不超过2次的概率和断头超过2次的概率分别为____,____。

28.如图4,在长方体A B C D-A1B1C1D1中,有一动点在此长方体内随机运动,则此动点在三棱锥A-A1B D内的概率为____。

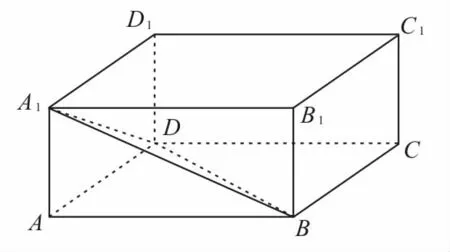
图4

29.在区间[0,1]上任取两个数a,b,则函数f(x)=x2+a x+b2无零点的概率为____。

30.如图5所示的茎叶图记录了甲、乙两个学习小组各4名同学在某次考试中的数学成绩,乙组记录中有一个数字模糊,无法确认,在图中用m表示。假设数字具有随机性,则乙组平均成绩超过甲组平均成绩的概率为____。

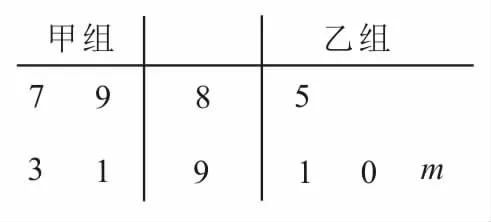
图5

31.已知某运动员每次投篮命中的概率都为40%,现采用随机模拟的方法估计该运动员3次投篮恰有2次命中的概率：先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中,再以每三个随机数为一组,代表3次投篮的结果。

经随机模拟产生了如下20组随机数：

907,966,191,925,271,932,812,458,569,683,431,257,393,027,556,488,730,113,537,989。

据此估计,该运动员3次投篮恰有2次命中的概率为____。

32.一只蜜蜂在一个棱长为3的正方体内自由飞行,若蜜蜂在飞行过程中始终保持与正方体6个表面的距离均大于1,称其为“安全飞行”,则蜜蜂“安全飞行”的概率为____。

33.小波通过做游戏的方式来确定周末活动,他随机地往单位圆内投掷一点,若此点到圆心的距离大于,则周末去看电影;若此点到圆心的距离小于,则去打篮球;否则,在家看书。则小波周末不在家看书的概率为____。

三、解答题

35.在一个不透明的箱子里装有5个完全相同的小球,球上分别标有数字1,2,3,4,5。甲先从箱子中摸出一个小球,记下球上所标数字后,再将该小球放回箱子中摇匀后,乙从该箱子中摸出一个小球。

(1)若甲、乙两人谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率。

(2)若规定：两人摸到的球上所标数字之和小于6,则甲获胜,否则乙获胜。这样的规定公平吗?

36.现有8个质量和外形都一样的球,其中A1,A2,A3为红球的编号,B1,B2,B3为黄球的编号,C1,C2为蓝球的编号,从三种颜色的球中分别选出一个球,放到一个盒子内。

(1)求红球A1被选中的概率。

(2)求黄球B1和蓝球C1不全被选中的概率。

37.长时间用手机上网严重影响学生的身体健康,某校为了解A,B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本绘制成茎叶图,如图6所示(图中的茎表示十位数字,叶表示个位数字)。

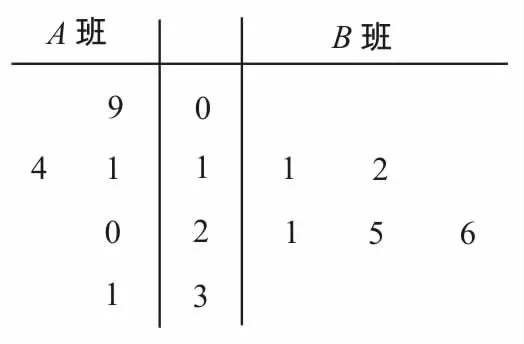
图6

(1)你能否估计哪个班级平均每周上网时间较长?

(2)从A班的样本数据中随机抽取一个不超过19的数据记为a,从B班的样本数据中随机抽取一个不超过21的数据记为b,求a＞b的概率。

38.某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付金额(单位：元)统计如表3所示。

表3

(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率。

(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中新司机获赔金额为4000元的概率。

39.设甲,乙,丙三个乒乓球协会的运动员人数分别为27,9,18。现采用分层抽样的方法从这三个协会中抽取6名运动员组队参加比赛。

(1)求应从这三个协会中分别抽取的运动员的人数。

(2)将抽取的6名运动员进行编号,编号分别为A1,A2,A3,A4,A5,A6。现从这6名运动员中随机抽取2人参加双打比赛。

①用所给编号列出所有可能的结果。

②设A为事件“编号为A5和A6的2名运动员中至少有1人被抽到”,求事件A发生的概率。

40.某出租车公司响应国家节能减排的号召,已陆续购买了140辆纯电动汽车作为运营车辆。目前我国主流纯电动汽车按续驶里程R(单位：k m)分为3类,即A类：80≤R＜150,B类：150≤R＜250,C类：R≥250。该公司对这140辆车的行驶总里程进行统计,结果如表4所示。

表4

(1)从这140辆汽车中任取1辆,求该车行驶总里程超过10万千米的概率。

(2)公司为了解这些车的工作状况,决定抽取14辆车进行车况分析,按表中描述的六种情况进行分层抽样,设从C类车中抽取了n辆车。

①求n的值。

②如果从这n辆车中随机选取2辆车,求恰有1辆车行驶总里程超过10万千米的概率。

41.甲打靶射击,有4发子弹,其中有1发是“空弹”。

(1)求“空弹”出现在第一枪的概率。

(2)求“空弹”出现在前三枪的概率。

(3)如果把“空弹”换成实弹,甲前三枪在靶上留下三个分别相距3,4,5的弹孔P,Q,R,第四枪瞄准了三角形P Q R射击,第四个弹孔落在三角形P Q R内,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小)。

42.某校从参加高三年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及各组频数如下：

[40,50),2;[50,60),3;[60,70),14; [70,80),15;[80,90),12;[90,100],4。

(1)请把给出的样本频率分布表(如表5)中的空格都填上。

(2)估计成绩在85分以上学生的比例。

(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在[90,100]中选两位同学,共同帮助成绩在[40,50)中的某一位同学。已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率。

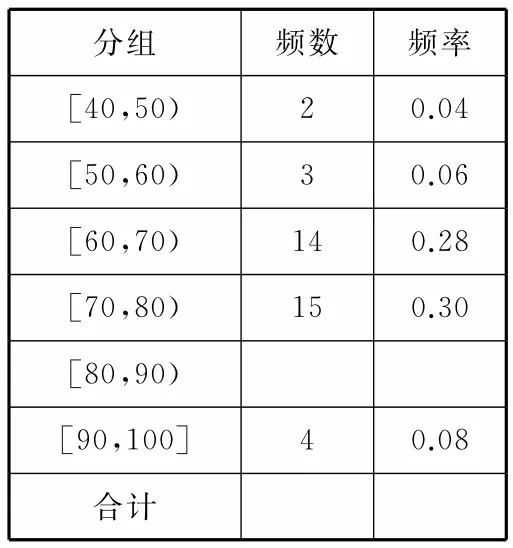
表5