古典概型与几何概型的区别及其求解
2018-04-12
几何概型是与古典概型最为接近的一种概率模型,两者的共同点是基本事件都是等可能的,不同点是基本事件的个数一个是无限的,一个是有限的。
求解概率问题的关键是弄清题中所研究的对象,准确求出试验与所求事件分别包含的基本事件的个数。
求解几何概型的概率问题时,首先要准确理解几何概型的意义,构造出随机事件对应的几何图形与度量区域(长度、面积或体积等),然后利用图形的几何度量来求随机事件的概率。当考查对象为点时,点的活动范围在线段上,用长度比计算概率;当考查对象为线段时,一般用角度比计算概率;当考查对象在某区域时,用面积比计算概率;当考查对象在某空间时,用体积比计算概率。
一、古典概型
解决古典概型的概率的关键是列举出所有可能的基本事件个数和符合条件的基本事件个数,这些基本事件都是等可能的。
例1某单位欲从包括甲、乙在内的5名应聘者中招聘2人,如果这5名应聘者被录用的机会均等,则甲、乙2人中至少有1人被录用的概率是____。
设其他3名应聘者为a,b,c,则从5人中录用2人的所有可能结果共有10种,列举如下:(甲,乙), (甲,a),(甲,b),(甲,c),(乙,a),(乙,b), (乙,c),(a,b),(a,c),(b,c)。
其中甲、乙2人至少有1人被录用的基本事件共有7种情况,列举如下:(甲,乙), (甲,a),(甲,b),(甲,c),(乙,a),(乙,b), (乙,c)。
例2投掷2枚骸子,则2个点数之和是6的概率为( )。

本题是一个古典概型问题。试验发生包含的基本事件是同时掷2枚骸子,共有6×6=36(种)等可能结果。而满足条件的基本事件是2个点数之和是6,共有5种等可能结果,列举如下:(1,5) (2,4)(3,3)(4,2)(5,1)。
二、与长度有关的几何概型
求解几何概型问题的关键在于弄清题中的考查对象和对象的活动范围。若一次试验中所有可能的结果和某个事件A包含的结果(基本事件)都对应一个长度,如线段长、时间的区间长、距离、路程等,那么需要先求出各自相应的长度,然后运用几何概型的概率计算公式求出事件A发生的概率。
例3利用计算机产生0~1之间的均匀随机数a,则事件“3a-1>0”发生的概率为____。
本题是考查几何概型概率的计算问题。可以将事件“3a-1>0”发生的概率转化为长度之比。
由3a-1>0,可得在0~ 1中对应的长度为,故所求概率为
例4在区间[0,2]上随机地取一个数x,则事件发生的概率为( )。

本题是考查几何概型概率的计算问题。
三、与角度有关的几何概型
同学们在解答几何概型问题时,容易混淆几何度量的比,尤其是角度比与长度比。当题中涉及一个变量时,可以观察变量可能到达的区域:若变量在线段上移动,则几何度量是长度;若变量在平面区域(或空间区域)内移动,则几何度量是面积(或体积)。
需要注意的是:当考查对象为线段时,一般用角度比计算概率;当点的活动范围在线段上时,一般用长度比计算概率。
例5如图1,四边形A B C D为矩形,以A为圆心,1为半径作圆弧D E交A B于E,在∠D A B内任作射线A P,求射线A P与线段B C有公共点的概率。

图1
因为在∠DA B内任作射线A P,则等可能事件为“在∠DA B内作射线A P”,所以它的所有等可能事件所在的区域Ω是∠DA B。当射线A P与线段B C有公共点时,射线A P落在∠C A B内,这时区域d为∠C A B=30°,所以射线A P与线段B C有公共点的概率为
例6如图2所示,在平面直角坐标系内,射线O T落在60°角的终边上,任作一条射线O A,则射线O A落在∠x O T内的概率是( )。

图2

记“射线O A落在∠x O T内”为事件M,射线O A落在平面直角坐标系内的每个位置的可能性是一样的。因为周角是360°,∠x O T=60°,所以所求概率
四、与面积有关的几何概型
与面积有关的几何概型是近几年高考的热点之一,归纳起来常见的命题方向主要是与三角形、矩形、圆等平面图形的面积有关的问题。当题设条件涉及两个变量时,一般与面积有关。求解与面积有关的几何概型时,要注意总的基本事件与所求基本事件分别表示的区域对应的面积。必要时可根据题意构造两个变量,把变量看成点的坐标,找到试验全部结果构成的平面图形,以便求解。
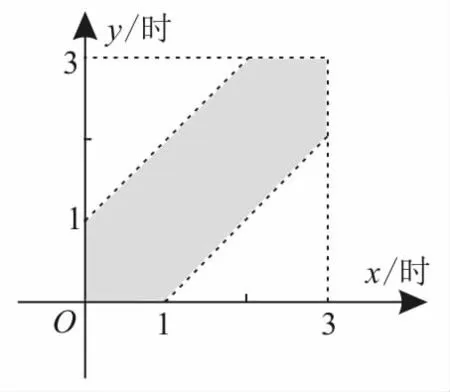
例7甲、乙两人约定上午9时至12时在某地点见面,并约定任何一个人先到之后等另一个人不超过一个小时,若对方一小时之内不来,则离去。如果他们两人在9时到12时之间的任何时刻到达约定地点的概率都是相等的,求他们见面的概率。
考虑甲、乙两人分别到达某地点的时间,在平面直角坐标系内分别用x轴、y轴表示甲、乙到达约定地点的时间,用0时到3时表示9时至12时的时间段,则试验发生包含的条件是{(x,y)|0<x<3,0<y<3}。
两人能见面的时间必须满足|x-y|<1,这就将所求问题化归为几何概型问题。
设9时后过了x小时甲到达,9时后过了y小时乙到达,取点Q(x,y),则0<x<3,0<y<3。
两人能见面所包含的条件是{(x,y)|0<x<3,0<y<3,|x-y|<1|}。作出两部分对应图形的区域,如图3所示。
五、与体积有关的几何概型
对于以体积为度量的几何概型问题,要根据空间几何体的体积计算方法,把概率计算转化为体积计算。解答与体积有关的几何概型问题时,先分清题目中的条件,找出几何体的形状,并计算出总体积,以及所求的事件占有的几何体的形状,并计算出体积,然后利用体积之比求出概率。
例8在一球内有一棱长为1的内接正方体,一点在球内运动,则此点落在正方体内部的概率为( )。
这是一个与体积有关的几何概型问题。由题意可得正方体的体积为V1=1。又球的直径是正方体的对角线长,故球的半径球的体积
六、几何概型的综合应用
例9如图4,在边长为3m的正方形中随机撒3000粒豆子,有800粒落到阴影部分,据此估计阴影部分的面积为____ m2。

图4
根据几何概型的概率的几何意义,可得到关于阴影部分面积的等式,解之即可。
由题意可得正方形的面积S1=3×3=9(m2)。
设阴影部分的面积为S2。
因为随机撒3000粒豆子,有800粒落到阴影部分,所以由几何概型的概率计算公式可得解得S2=2.4(m2)。
例10已知函数f(x)=2x2-4a x+2b2,若a∈{4,6,8},b∈{3,5,7},则该函数有两个零点的概率为____。
要使函数f(x)=2x2-4a x+2b2有两个零点,即方程x2-2a x+b2=0要有两个实根,则Δ=4a2-4b2≥0,即a≥b。
由a∈{4,6,8},b∈{3,5,7},可知a,b的所有取法共有3×3=9(种),其中满足a≥b的取法有(4,3),(6,3),(6,5),(8,3),(8,5),(8,7),共6种,所以所求概率为
