改进遗传算法的风、光互补发电系统优化设计
2018-04-11于文英王玟苈马新秀张占先武新芳罗晓婧刘永生
于文英, 王玟苈, 马新秀, 张占先, 武新芳, 罗晓婧, 刘永生
(上海电力学院 太阳能研究所, 上海 200090)
0 引 言
在风光互补发电系统中,由于对各发电装置之间存在复杂的约束关系[1],因此,可以通过合理分配各发电装置来得到稳定的功率输出。基于风光互补发电系统本身发电过程的复杂性,以及系统部件自身的非线性特征,使得优化过程本身也是非线性的[2-3]。一般解决系统优化的方法是建立简单和线性的系统数学模型,或者是建立相对复杂的数学模型,但这都是在一定的范围内随机选择一些部件容量进行比较的。而在一些居民分散、交通不便以及电网不能覆盖的无电地区,建立合适风光互补发电系统则是一个比较不错的选择[4]。
遗传算法作为一个对优化比较强的技术,是目前解决非线性问题较好的一种方法,而且也不依赖于某个具体的领域[5-7]。本文对风光互补发电系统提出的改进遗传算法,通过对组件特性采取更精准的数学模型,构造出系统投资成本、运行成本尽可能低,输出功率尽可能大的多目标函数[8]。对于实际工程而言,我们的最终目的就是求得目标函数的最大值或是最小值,而遗传算法可以获得更高的收敛能力和搜索效率。经国内外相关领域的专家学者研究证实,遗传算法完全能够处理风光互补发电系统各发电装置之间复杂的结构关系。
1 风光储系统建模
1.1 光伏发电系统模型
光伏发电系统的等效电路图如图1所示,其输出功率可模拟为:
Ppv=UpvIph-Id-IRsh
(1)
光伏系统的初投资成本可模拟为:
S=Cgen+Cinv+Cinst
(2)
式中:Iph为光生电流,Id为流过二极管的内部电流,IRsh为流过电阻Rsh的电流,Upv为光伏电池单元的电压,Cgen为发电成本(元/kWh),Cinv为逆变器成本(元/kWh),Cinst为安装成本(元/kWh)。
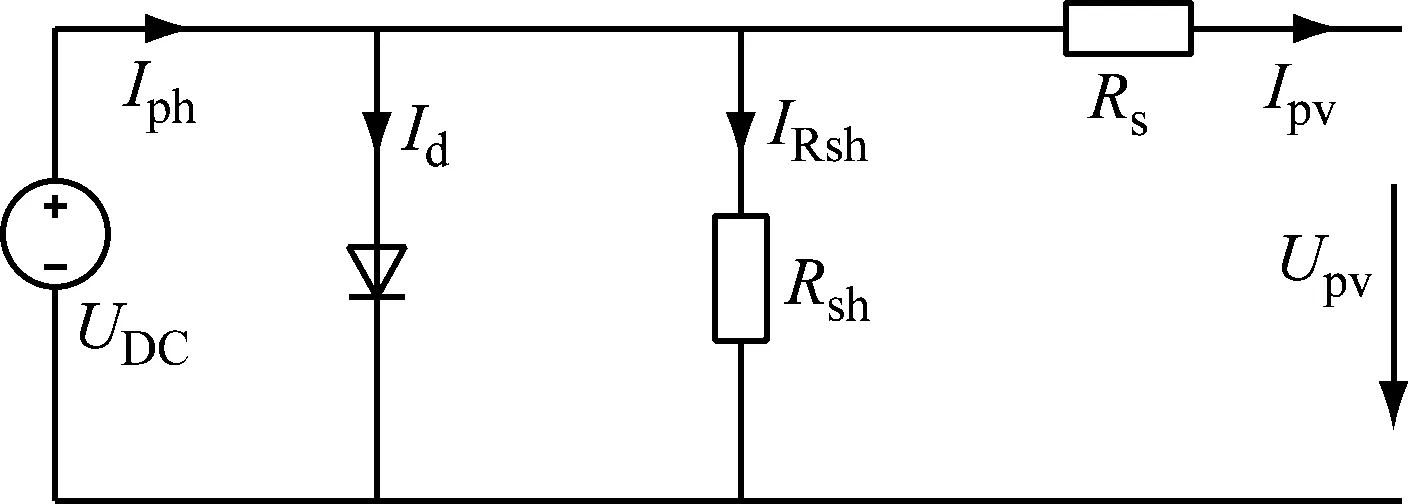
图1光伏发电系统等效图
图中,UDC为等效太阳能电池模块;且光伏电压Upv与电流Ipv为关联参考方向,P的值为正时是消耗,P为负时是发出的功率。
1.2 风力发电系统模型
风电场的经济性能应考虑的成本包括:初投资成本、故障维修和清洗费用、税收利息等。风力发电系统在不同风频状况时的输出功率为[9]:
(3)
式中:PR为风力发电动机的额定功率,vc为启动风速,vR为额定风速,vF为截止风速,k为韦布尔形状参数。
1.3 蓄电池模型
蓄电池在系统中担任了能量缓冲的任务,其容量配置关系整个系统是否能稳定运行。当负荷的用电需求量低于风光互补发电的总发电量时,蓄电池的容量可表示为[10]:
(4)
当负荷的用电需求量高于风光互补发电的总发电量时蓄电池的容量可表示为:
Cbat(t)=Cbat(t-1)(1-σ)-
PLoad(t)/ηinv-Ptot(t)
(5)
式中:Cbat(t)、Cbat(t-1)分别为在t和t-1时刻时可用的电池容量;Ptot(t)为t时刻光伏和风能的发出的电功率总和;Ppv(t)为t时刻光伏发出的电功率;PWG(t)为t时刻风力发出的电功率;Pload(t)为t时刻负荷消耗的电功率;σ为蓄电池本身放电率(一般每半年自释放25%);ηbat为电池充放电效率;ηinv为逆变效率(一般为92%)。
2 多目标优化设计的系统建模
2.1 经济性指标
目前社会对电源系统的最低能源成本有了更多的关注,对于混合系统的经济性分析的概念也被广大研究者认可,它成为优化系统的一种重要因素。在本文中,采用系统能量均摊成本(Levecized cost of energy, LCE)的方法来确定总年度成本与每年的电力输出之间的比例的大小。净现值是一种对工程进行财政评估的标准方法,它可以对发电系统每千瓦时的能量进行经济性研究和分析[11]。结合这两种基本经济指标,我们得到经济指标函数为:
(6)
式中,n为光伏系统的安装时间(年)。
系统的初投资费用主要包括购买设备、人工安装费、通信费等[12]。在本文的研究中,人工费、安装费、通信费总费用为光伏电池板的40%及风力发电动机的20%。因此维护的费用数据可以参照表1所示。
本系统使用寿命为25 a,维护费的现值表示为:
MC=MC0×T=mIC×T
(7)
式中:Pout为系统每年输出功率;IC为设备初投资;MC为维护费的现值;RC是重置设备成本现值;i为折现率;MC0为第1年的维护费用;m为第1年的维修费用与系统总费用之比。

表1 系统各部件的价格、维修费用、寿命列表
系统的重置成本费用现值是指在整个系统寿命周期内所有替代成本发生的净现值[13]。本文认为只有蓄电池需要定期更换,其他设备认为在整个周期内没有损坏。那么,系统的重置成本费用现值可表示为:
(8)
式中:Qc为蓄电池的单位容量成本,元/Ah;Cbat为所选择的蓄电池的容量,Ah;g为系统的设备更换的通货膨胀率,2009年数据为6%;i为系统的设备更换的贴现率,一般认为为8%;N表示在整个T时间内,组件需更换的次数,本文中N取5。
基于以上所述,对式(7)、(8)进行整理得:
(9)
式中:IC表示设备初投资;MC表示系统的维护费用;RC表示系统的重置成本现值;NWG×CWG表示风力发电动机组的装机容量;NPV×CPV代表光伏电池板的装机容量;NB×CB为蓄电池的容量。
2.2 功率最大化指标
每一位用户都希望发电系统尽可能输出其最大的功率,但是在一些风光资源比较丰富的地区,建立合理的风光互补系统才能使资源浪费最小化,经济效益最大化。因此需要的另一个指标就是尽可能的使输出功率最大化。
2.3 系统可靠性指标
对于离网系统,国外不少文献提出用负载损失概率LPSP来衡量它的可靠性指标[12-13]。当LPSP=0时,表示负荷的用电需求在任何时候都能够满足,可靠性为100%;LPSP=1,则表示在所有时间内都不能满足负载用电需要。一般情况下,系统的LPSP值都在0到1之间。
对于负载需求的电量低于风光互补系统的总发电量时,能量过剩,这时将会向蓄电池充电,直到将蓄电池电充满为止。过剩的能量为本系统产生但是没有被利用的部分,用WE(t)来表示:

(10)
当风光互补总发电量不能达到负载需求的电量时,即此时能量缺损,蓄电池向负载放电,直到将蓄电池电放完为止。如果蓄电池电量降至它的最低水平Cbat min,则控制系统将与负载断开连接,负载损失时间th,此时的缺电量LPS[14-15]为:
LPS(t)=Pload(t)Δt-Ptot(t)+
(11)
式中:DOD为放电深度;认为光伏发电与风力发电均是连续的。
在某段时间范围内,负荷电量的缺失量与负荷总需求电量的比值称作负荷缺电率(LPSP),又叫发电系统的发电量不能满足负载用电量的概率。在设计当中,为了避免加大混合发电系统各部件的容量,系统的LPSP值不能过高。一般情况下,LPSP值在0到1之间。LPSP可表示为:
(12)
2.4 多目标优化设计模型
把经济性LCE最佳化、Pout输出最大化,LPSP最优作为优化设计的3个目标[16],则关于多目标函数的模型就可以表示为:
(13)
3 多目标遗传算法的改进
遗传算法本质上是一种不依赖于任何具体问题的直接搜索方法,其后代由于遗传了父母的基因,在新一轮的环境中竞争,不断进化,最后一组适应性最强的个体因为最适应环境而收敛,即得到了问题的最优解[17-18]。如图2、3所示为本文所采用的改进遗传算法和优化设计的流程图,其模型求解过程如下。
3.1 编码
本文中多目标模型涉及3个变量:NPV、Nw、Nb,并且这3个变量是非线性相关的。由于二进制编码及解码操作简单,故本文对3个变量采用二进制编码方法,然后根据自身的约束条件对这3个变量的位串长度进行合理的设置[19]。程序中NPV、Nw、NB设定的范围为:[1,1,1;10,5,10]。
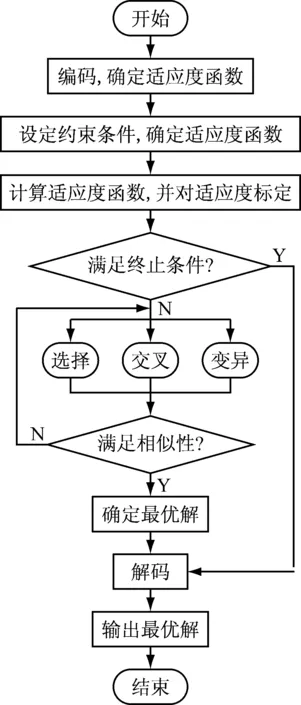
图2改进遗传算法程序流程图
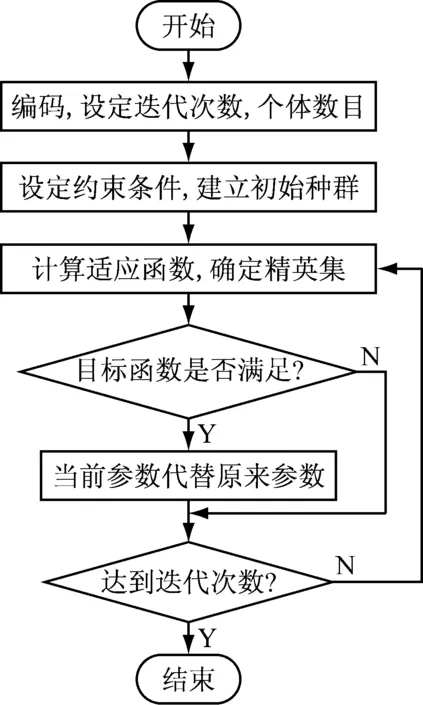
图3多目标算法流程图
3.2 初始化
初始化主要有3个部分组成:
① 设定种群大小,精英解集大小,设置交叉和变异概率;② 建立初始种群,并设定性能跟踪,并将求解的区域按照多目标函数的约束条件划为多个符合要求的子区域;③ 随机产生个体。首先在变量范围区域内随机产生个体,保留符合要求的个体作为初始个体,反之,再重新随机产生新的个体。由于风力机、PV组件和蓄电池之间的搭配存在约束关系,为了达到能量转换的要求,需要进行多次随机初始化,每次都要进行判断,计算量大。
3.3 选择
首先通过计算适应度函数来分配适应度值,多目标函数中采用随机遍历采样选择函数,被选中的个体加入精英集,同时剔除掉集合中的劣解,这样就能够形成一个全新的精英集[20]。
3.4 交叉
交叉的目的是为了防止个体过早收敛,对于每个个体来讲,都存在一定的概率被选中。对于当前的种群,选择其中一对个体进行单点交叉,交配后产生新的种群。
3.5 变异
使用二进制和整形变异函数Mut,变异按照初始化设定的概率值进行,且在位串中随机选择位置。变异的结果也有可能出现倾角越出预设范围的情况,则再次按照预设的概率进行变异,直到产生足够的个体。
4 设计实例
在上海南汇地区,当地的气象资料及用户的用电需求如图4所示,计算得出的单片光伏电池的输出功率、600 W风力发电动机的输出功率如图5、6所示。在保证系统正常运行的情况下,对光伏组件、风机和蓄电池选取合适的的类形及数量,一方面确保系统发电量得到较大的输出,另一方面使LCE和LPSP的值尽可能的低[21]。

图4负载每天用电量
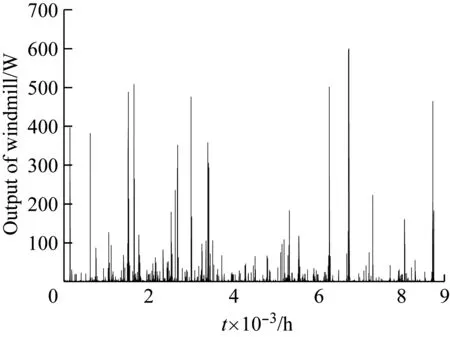
图5风力发电动机逐小时输出功率的全年分布
选用HGE-600H型风力发电动机,EAR SOLARTECH-100W型PV组件,100Ah-24 V蓄电池。个体数目、最大遗传代数和变量的二进制位数分别设为300、100和20[22]。迭代100次后,程序运行结果如图7所示。由图7可以看出:3个目标函数的解的变化基本稳定,但是种群均值的变化很大,在振荡中趋于稳定。第1目标函数(LCE)振荡最为明显,其次是第3目标函数(LPSP),第2目标函数(Pout)最为稳定。从迭代100次后的精英集中选择了以下6种方案,如表2所示。

图6 全年单片太阳电池输出功率

(a)LCE目标函数(b)Pout目标函数

(c)LPSP目标函数(d)3目标函数
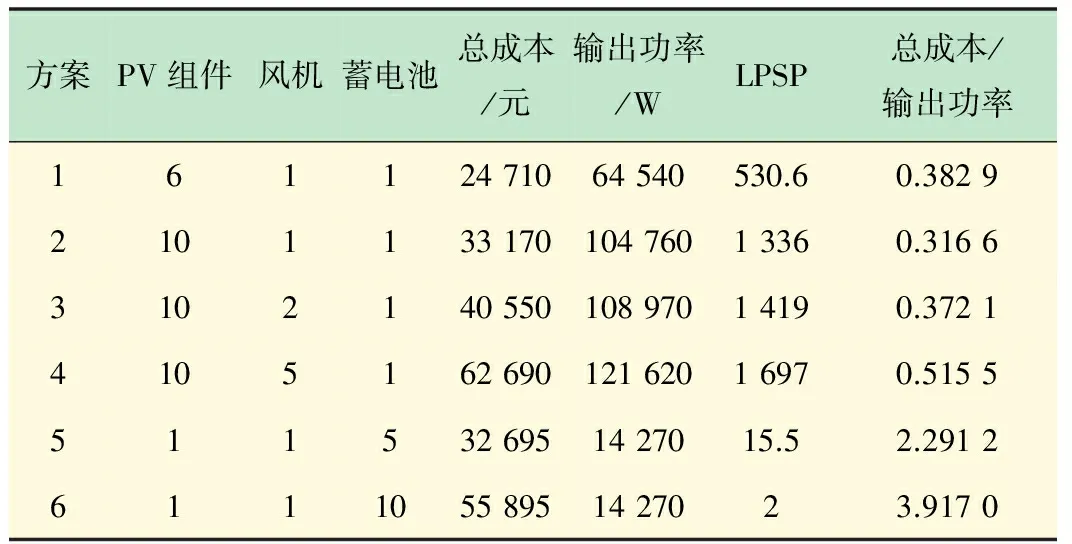
图7 目标函数迭代100次后的最优解及性能跟踪
从表2中可以看出:风力机数量、蓄电池数量已定时(例如为1),随着PV组件数量的增加,总成本/输出功率值是越来越低;PV组件数量、蓄电池数量已定时(例如PV为10,蓄电池为1),风力机数量越大,总成本/输出功率值是越来越高;风力机数量、PV组件数量已定时(例如为1),随着蓄电池数量的增加,总成本/输出功率值是越来越高。造成这种现象的原因主要有:
(1) 在南汇地区,风力资源较差,输出功率很小,这必然导致风力发电效率低,严重影响系统可靠性指标LPSP及总成本/输出功率值。
(2) 在3种装置当中,蓄电池的发电成本最高,其额定功率的增大必然会增大系统的成本。为达到互补的效果,应尽量增加PV组件或者是风力发电动机,尽量少用蓄电池,从而减小整个系统的单价成本。
5 结 语
本文通过建立以经济性指标LCE,功率最大化指标Pout,max和系统可靠性指标LPSP为多目标函数的数学模型,确定合适的风力机、PV组件和蓄电池的类型数量。同时改进的遗传算法可以根据种群个体的分布情况,利用控制参数自适应调整策略,获得更高的全局收敛能力和更快的搜索效率。且以上海南汇地区某用户的需求为例,验证了该方法的有效性,取得了良好的效果。
参考文献(References):
[1]Alessandra Parisio, Evangelos Rikos, George Tzamalis,etal.Use of model predictive control for experimental microgrid optimization [J]. Applied Energy, 115(2014):37-46.
[2]毛晓明, 陈深, 吴杰康, 等. 分时电价机制下含蓄电池微网的经济调度[J]. 电网技术, 2015,39(5):1192-1197.
[3]陈洁, 杨秀, 朱兰, 等. 微网多目标经济调度[J]. 中国电动机工程学报,2013,33(19):57-66.
[4]林虹江, 周步祥, 胡庆有, 等. 基于风光互补电力入网的电力系统动态经济调度[J]. 可再生能源, 2014, 32(11):1671-1678.
[5]朱兰, 严正, 杨秀, 等. 计及需求侧响应的微网综合资源规划方法[J]. 中国电动机工程学报,2014,34(16):2621-2628.
[6]曾博, 欧阳邵杰, 张建华, 等. 考虑复杂预想场景下光伏高效利用的微电网综合规划[J]. 中国电动机工程学报,2014,34(25):4259-4269.
[7]Yin ZiHeng, Li Peng, Dou Pengchong,etal. Reaearch on mechanical properties of disel generator with loop shaping optimization control for islanded microgrid frequency[J].Applied Mechanics and Materials,508(2014):200-203.
[8]Liu Yongsheng, Gu Minan, Zhao Chunjiang. Economical and environmental analysis for the photovoltaic noise barrier system in Shanghai, China[C]∥Proceedings of the IASTED International Conference on Modeling, Simulation, and Identification (MSI 2009). Beijing, 2009:658-230.
[9]杨苏, 袁越, 陆丹, 等. 基于风速-负荷联合状态的发输电系统可靠性评估研究[J]. 可再生能源, 2016, 34(7):1024-1031.
[10]Mokheimer EMA, Al-Sharafi A, Habib MA,etal. A new study for hybrid PV/Wind off-grid power generation systems with the comparison of results from homer [J]. International Journal of Green Energy, 2015, 12(5):526-542.
[11]Gamarra Carlos, Guerrero Josep M. Computational optimization techniques applied to microgrids planning: a review [J]. Renewable and Sustainable Energy Reviews,48(2015):413-424.
[12]Sechilariu Manuela, Wang Bao Chao, Locment Fabrice. Supervision control for optimal energy cost management in DCmicrogrid:Design and simulation[J]. Electrical Power and Energy System,58(2014):140-149.
[13]Hina Fathima A, Palanisamy K. Optimization in microgrids with hybrid energy system-a review [J]. Renewable and Sustainable Energy Reviews,45(2015):431-446.
[14]Maleki A, Pourfayaz F. Optimal sizing of autonomous hybrid photovoltaic/wind/battery power system with LPSP technology by using evolutionary algorithms [J]. Solar Energy, 2015, 115:471-483.
[15]Belmili H, Haddadi M, Bacha S,etal. Sizing stand-alone photovoltaic-wind hybrid system: Techno-economic analysis and optimization [J]. Renewable & Sustainable Energy Reviews, 2014, 30(2):821-832.
[16]何舜, 郑毅, 蔡旭, 等. 微网能源系统的滚动优化管理[J]. 电网技术,2014,38(9):2349-2355.
[17]赵媛媛, 袁澎, 艾芊, 等. 考虑拓扑约束并采用改进遗传算法的PMU优化配置[J]. 电网技术,2014,38(8):2063-2070.
[18]孙涛, 孙文磊, 何连英. 基于遗传算法的风力机可靠性优化分配方法研究[J]. 可再生能源, 2016, 34(5):699-704.
[19]Dufo-López R, Cristóbal-Monreal IR, Yusta JM. Optimisation of PV-wind-diesel-battery stand-alone systems to minimise cost and maximise human development index and job creation [J]. Renewable Energy, 2016, 94:280-293.
[20]李绍金, 周任军, 周胜瑜,等. 电力系统环保经济负荷分配的模糊自修正粒子群算法[J]. 电力系统保护与控制,2014(8):15-21.
[21]龚正宇, 刘继春, 武云霞,等. 含风光储的多微网接入配网的联合调度策略[J]. 可再生能源, 2014, 32(11):1665-1670.
[22]Huang Jingfang, Honggang N G, Yi A N.Priority-based traffic scheduling and utility optimization for cognitive radio communication infrastructure-based smart grid[J].IEEE Transactions on Smart Grid, 2013, 4(1): 78-86.
