MEMS手势轨迹绘制系统设计
2018-04-11李明哲宋华军
邵 帅, 李明哲, 许 睿, 宋华军
(1. 中国石油大学(华东) 信息与控制工程学院,山东 青岛 266580; 2. 天津大学 电气自动化与信息工程学院,天津 300072)
0 引 言
传统的人机交互方式包括触摸屏、语音识别等存在一定的局限性,比如触摸屏必须限定在设备屏幕上使用;语音识别技术在嘈杂环境中或使用方言时效果不尽人意。而基于MEMS惯性传感器的无接触轨迹重构手势识别方式,弥补了传统的人机交互方式的不足,具有直观、自然、易于学习等优势,可应用在无接触手写电子笔[1],体感游戏,空中鼠标,遥控器空中写数字换台等处。
捷联惯性导航技术具有很强的抗干扰能力,随着近20年微电子机械系统(Micro Electro Mechanical System,MEMS)的较快发展[2],捷联惯导技术得到进一步完善。MEMS惯性传感器包括陀螺仪和加速度计,具有成本低、体积小、质量轻、功耗低、灵敏度高、易于集成,以及适应性强等特点,对于智能手机等移动设备而言,基于MEMS惯性传感器的手势识别方法比基于视频的识别方法更为适用。
已有系统多采用独立的陀螺仪、加速度计等多个传感器组合进行姿态解算,存在多个芯片占用空间大、姿态数据存在轴间误差、数据融合精度欠佳等不足。本文设计了基于MEMS的手势轨迹绘制系统,选取集成加速度计、陀螺仪和磁力计于一体的MPU9250为核心芯片,用来采集九轴原始数据,包括三轴加速度、三轴角速度和三轴磁场。然后在STM32单片机上进行姿态解算,最后通过蓝牙将原始数据和姿态数据传给上位机,在上位机完成轨迹重构。
1 系统硬件部分设计
1.1 硬件结构设计
硬件电路核心为STM32F4单片机与MPU9250芯片。电路采用USB接口供电,通过3.3 V稳压芯片,确保电源输出稳定电压,保证芯片正常工作。通过A/D转换计算电池电量,在电池电量不足时控制LED灯报警。MPU9250芯片作为数据采集芯片,无需A/D转换器就可直接将数据通过I2C传送到单片机中进行处理,减小系统能耗。同时外接蓝牙模块,与上位机进行交互,结构图如图1所示。
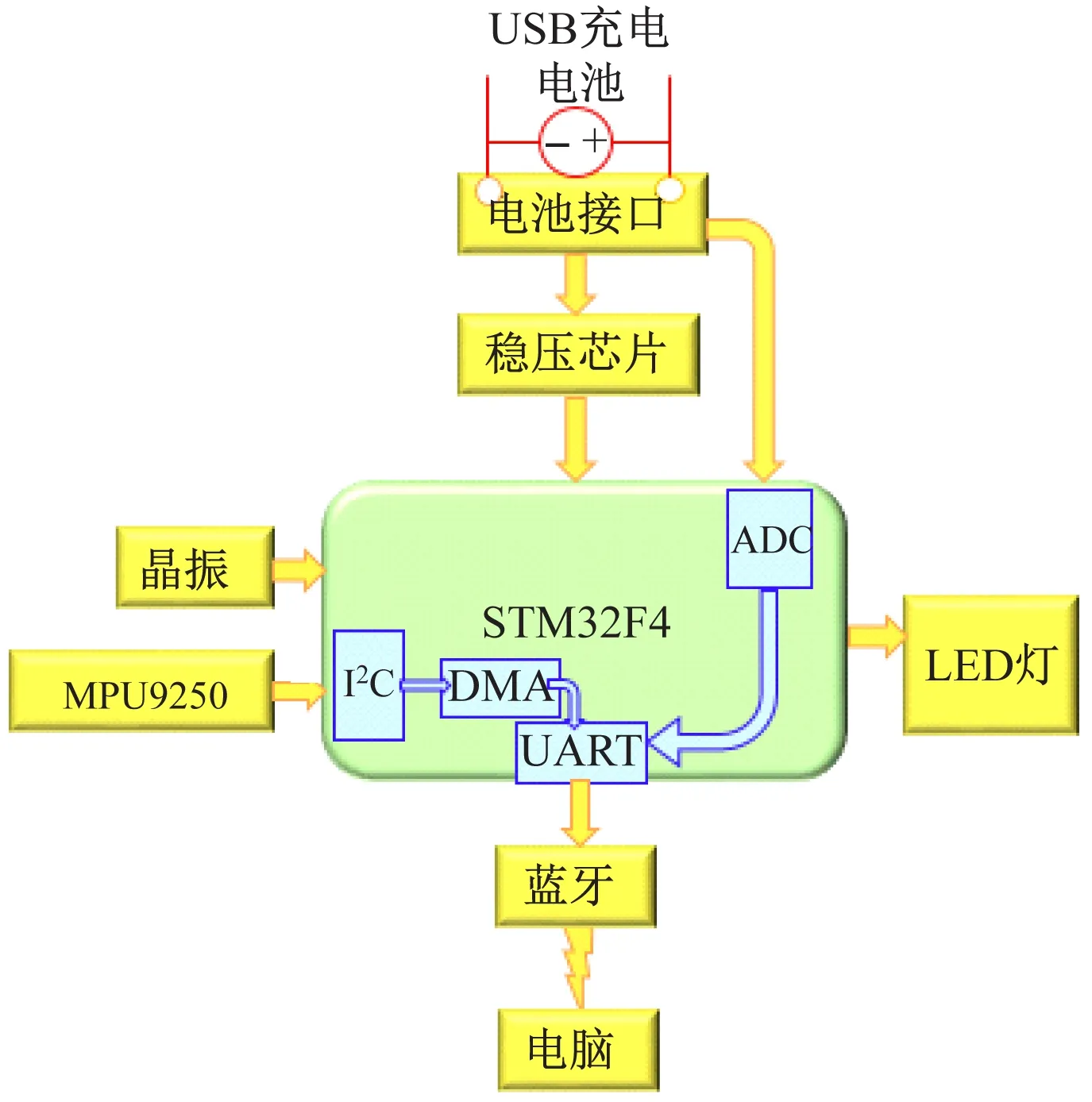
图1 硬件部分结构图
1.2 硬件系统的软件流程
软件流程图如图2所示。单片机上电后,首先对各个模块进行调试,当调试完成后,对系统初始化, MPU9250采集原始数据并发送到单片机中,单片机接收数据后,运行姿态解算算法,当检测每完成一个手势动作后,都触发一个外部中断,让姿态解算算法重新运行。在解算同时,将原始九轴数据和解算好的四元数通过蓝牙模块实时传给上位机。
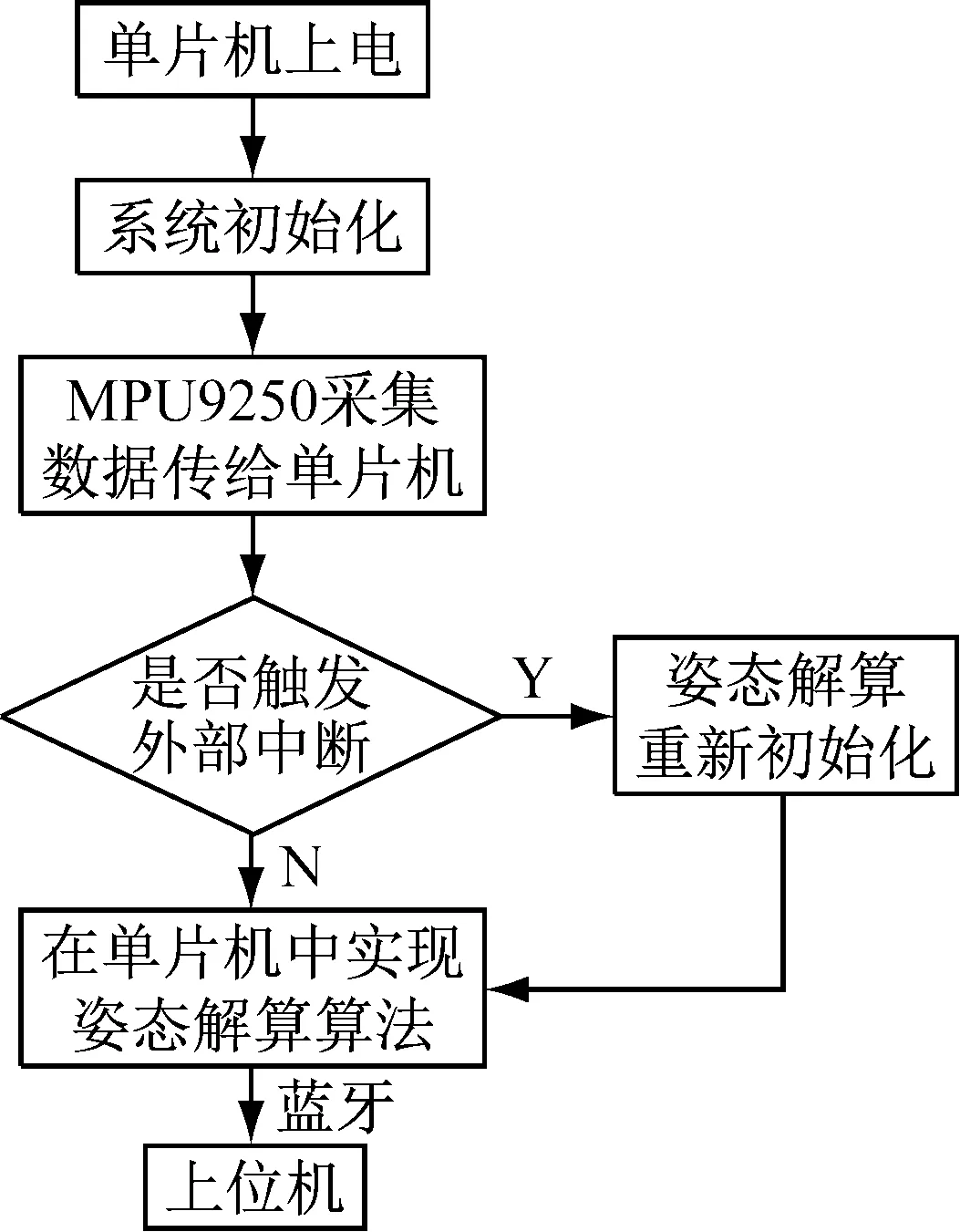
图2软件流程图
2 系统实现算法
2.1 算法流程
整个系统的算法流程图如图3所示,在一个完整手势流程内,MPU9250采集九轴数据后,先用其中的三轴加速度和三轴磁场数据计算初始欧拉角,其中MPU9250测的三轴加速度数据被称为载体坐标系[3]加速度。然后将初始欧拉角转换为初始四元数,再与三轴角速度结合,根据陀螺积分的方法更新下一时刻的四元数,直到这个手势流程结束。根据每个时刻的四元数与载体坐标系加速度计算出该时刻地理坐标系[3]加速度,再对地理坐标系加速度进行双重积分得到每个时间段的位移,最终形成相应轨迹。
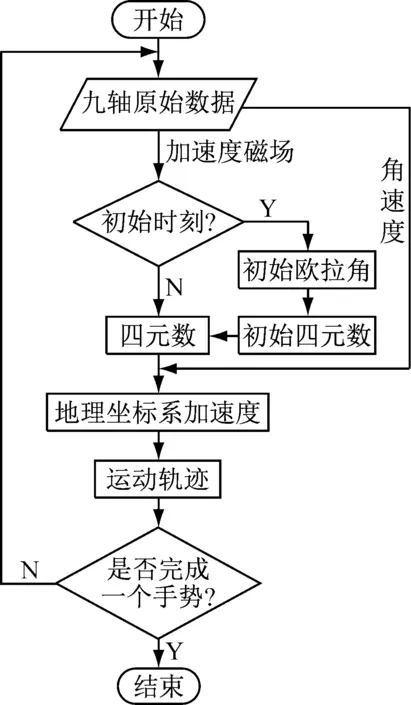
图3算法流程图
2.2 初始姿态解算原理
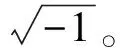
载体坐标系(b系)中,MPU9250采集的加速度值可表示为acc=[axb,ayb,azb]T,磁场强度可表示为mag=[mxb,myb,mzb]T。在平稳状态下,地理坐标系(n系)中,重力场G=[0,0,-g]T,磁场强度M=[0,my,mz]T,可在载体坐标系中由下式表示为:
(1)
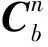
(2)
ψ,θ,Φ分别代表绕z、y、x轴转动角度。
将式(2)代入式(1)可得:
(3)
式中:D为磁偏角,是一个固定值,可由查表或大量实验得到。此种用加速度和磁力结合的解算方法,只适用于物体静止或低动态的情况,所以在确定初始姿态时应该让物体保持静止10 s时间,然后采集该10 s数据的平均值作为测量值。得到初始的欧拉角以后,通过下式将初始的欧拉角转换成初始的四元数:
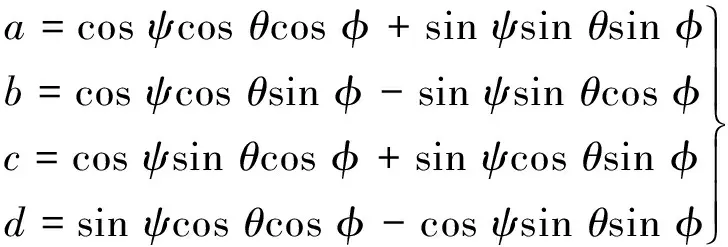
(4)
需要注意的是,绕坐标轴不同的旋转顺序会得到不同的四元数公式,式(4)是按照绕“zyx”的顺序得到的。
2.3 姿态的更新
在得到初始姿态后,可根据惯导原理,对姿态不断进行更新,更新方程为:
(5)

(6)
式中:ωx,ωy,ωz分别代表t-1时刻的三轴角速度;Δt是采样间隔。根据式(6)可得不断更新的四元数,在初始四元数较准确的前提下,此时在高动态时也可有较高的准确率。
2.4 轨迹重构
在求轨迹时,应先通过下式,将载体坐标系加速度转换成地理坐标系加速度。
(7)
式中:axb,ayb,azb表示载体坐标系下的三轴加速度;axn,ayn,azn表示地理坐标系下的加速度。
该系统采集的加速度都是以“g”为单位,所以在双重积分求得轨迹之前,先通过下式,将加速度的单位转换成标准单位(m/s2)。其中z轴的加速度,要去掉重力的影响。
axN=axng,ayN=ayng,azN=(azn-1)g
(8)
式中:axN,ayN,azN表示地理坐标系下,不受重力影响具有标准单位的三轴加速度。
根据式(9)求三轴加速度的向量模,然后设定一个阈值,只有在当向量模大于该阈值时,系统才会被判断为在进行轨迹重构,
(9)
通过下式分别对三轴的加速度进行双重积分,可求得载体在三轴上的位移,分别由Sx,Sy,Sz表示:
Sx=∬axNdt,Sy=∬ayNdt,Sz=∬azNdt
(10)
3 实验结果分析
设计的手势轨迹绘制系统电路板如图4所示,板大小为35 mm×17 mm。
3.1 “对号”实验
手拿传感器画“对号”,相应加速度如图5所示。

图4 电路板

(a) 载体坐标系
(b) 地理坐标系
解算的四元数如图6所示。“对号”图如图7所示。

(a)(b)(c)(d)
图6画对号解算的四元数
由图5~7可看出,该系统在做手势画“对号”时,清晰地展现了图形的形状和尺寸大小。
3.2 “8”实验
手拿传感器在空间写“8”,相应加速度见图8,相应四元数见图9,数字“8”如图10所示。
由图8~10可见,在空间中画闭环图形时,只要调整观看图形时的角度,也可得到图形清晰的形状和尺寸大小。
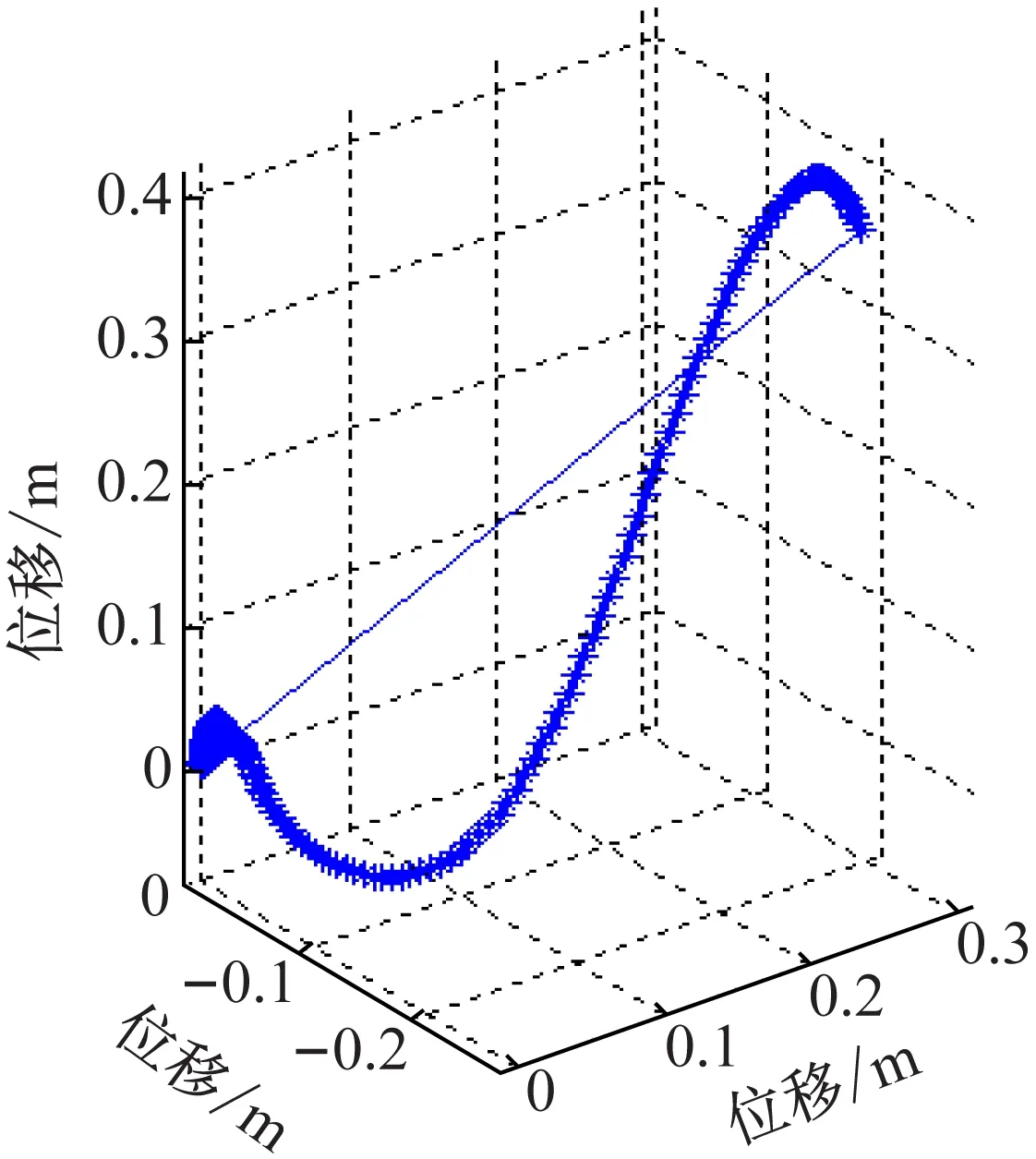
图7 对号图

(a) 载体坐标系

(b) 地理坐标系

(a)(b)(c)(d)
图9画数字“8”解算的四元数
这两组实验分别完成了此系统在空间中开环图形和闭环图形的绘制,都可以清晰、直观地反映该系统的工作效果,能够完成轨迹的正确绘制。
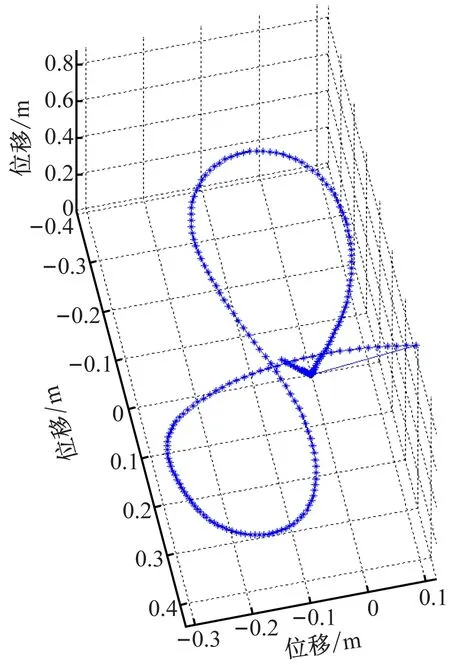
图10 数字“8”三维图
4 结 语
本文设计的系统完成了系统硬件的制作,并对原始数据进行处理,最后在上位机生成轨迹。实验结果充分证明了解算算法和轨迹重构的可行性。
该系统因为采用陀螺积分的方法更新四元数,所以在长时间应用中会产生积分漂移从而造成生成的四元数误差,本文采用设置中断的方式来减小积分时间从而减小误差,但根据加速度膜的大小来判断手势轨迹完成与否有时会产生误判,并且每次中断以后重新计算初始四元数时,不能保证每次都在平稳环境下计算,也会产生计算误差。在后续研究中,将考虑广义卡尔曼滤波与惯性导航知识相结合的方法来进行解算研究。
参考文献(References):
[1]Leong H W,Li W J. Handwriting tracking based on coupled IMU/electromagnetic resonance motion detection[C]//International Conference on Robotics and Biomimetics. Sanya,2007:377-381.
[2]王淑华.MEMS传感器现状及应用[J]. 微纳电子技术,2011,48(8):516-522.
[3]张天光,王秀萍,王丽霞.捷联惯性导航技术[M].2版.北京:国防工业出版社,2007.12.
[4]王粉花, 张万书. 基于手势识别技术的3D虚拟交互系统[J]. 实验室研究与探索, 2014, 33(6):94-98.
[5]陈孟元, 谢义建, 陈跃东,等. 基于四元数改进型互补滤波的MEMS姿态解算[J]. 电子测量与仪器学报, 2015, 29(9):1391-1397.
[6]夏龄, 周德荣, 陈鹏,等. 基于手势识别的S195型柴油机虚拟装配[J]. 实验室研究与探索, 2015, 34(9):84-86.
[7]常敏, 崔永进, 何蓓薇,等. 四轴飞行器姿态控制系统设计[J]. 通信电源技术, 2015(5):144-147.
[8]谢宁, 毕俊熹, 娄小平,等. 融合多传感信息的仿人机器人姿态解算[J]. 电子科技, 2015, 28(1):150-154.
[9]仇立杰. 基于MEMS传感器的手势识别算法研究[D]. 北京:北京化工大学, 2016.
[10]Srihari S N, Cha S H, Arora H,etal. Individuality of handwriting: A validation study[C]// International Conference on Document Analysis and Recognition. IEEE Computer Society, 2001:106.
[11]季怡, 杨帆, 龚声蓉,等. 基于Adaboost实现的实时手势识别[J]. 实验室研究与探索, 2014, 33(8):123-126.
[12]周树道, 金永奇, 卫克晶,等. 采用卡尔曼滤波算法的MEMS器件姿态测量[J]. 实验室研究与探索, 2015, 34(2):38-42.
[13]《实验室研究与探索》编辑部. 航天器姿态控制新型惯性执行机构技术[J]. 实验室研究与探索, 2009, 28(10):I0001-I0002.
[14]张荣辉, 贾宏光, 陈涛,等. 基于四元数法的捷联式惯性导航系统的姿态解算[J]. 光学精密工程, 2008, 16(10):1963-1970.
[15]Lagardere X, Gonzalez A. Gesture recognition: US, US7372993[P]. 2008.
[16]Mitra S, Acharya T. Gesture recognition: A survey[J]. IEEE Transactions on Systems Man & Cybernetics Part C, 2007, 37(3):311-324.
